0.   引言

煤矿井下作业环境复杂多变，存在各种障碍物和危险因素，传统的人工巡检存在各种安全危险问题，应用煤矿足式机器人进行巡检不仅能保障矿工生命安全，还能提高井下作业效率。其中机器人路径规划是煤矿足式机器人自主导航的核心模块，也是技术难点之一。

机器人路径规划算法是寻找机器人抵达某一目的地所需要行走的最优路径，其评价指标包括寻路速度、路径长短等。机器人路径规划算法包括全局路径规划算法和局部路径规划算法。全局路径规划算法又称离线算法，包括Dijkstra算法^[1]、A^*算法^[2]、快速搜索随机树（Rapidly-exploring Random Tree，RRT）^[3]、概率路图法^[4]、遗传算法^[5]、蚁群算法等^[6]。全局路径规划算法在给定的起始点和目标点之间寻找出最短路径，但规划完路径后无法对路径上后续新增障碍物及时进行再次路径寻优。局部路径规划算法又称在线算法，包括人工势场法^[7]（Artificial Potential Field, APF）、时间弹性带法^[8]（Timed Elastic Band，TEB）以及动态窗口法^[9] （Dynamic Windows Approach, DWA）等。局部路径规划算法可实时计算机器人自身的方向、速度等参数并及时对机器人进行控制，可避开路径上新增的障碍物，但一般无法实现复杂环境下的避障工作，特别是机器人在遇到某些障碍物密集环境、“L”型和“U”型障碍物时会出现“假死”状态。

目前大多路径规划算法都是全局路径规划算法和局部路径规划算法结合使用^[10-11]。A^*算法原理简单、计算效率高、易于改进与优化，因此得到广泛研究和应用^[12-14]。文献[15-16]对A^*算法进行改进，通过融合转折点的方式减少路径上的拐点数量，所得路线更平滑，但寻路性能提升有限。文献[17-18]对A^*算法进行改进，并结合其他算法加快收敛速度，大幅提高了计算效率，然而避障性能仍有提升空间。文献[19]提出了一种改进A^*算法与增强型DWA相结合的机器人路径规划方案，对搜索点选择策略和代价函数进行了优化，提高了路径规划效率，但对DWA在密集障碍物环境下出现“假死”的问题缺少讨论。文献[20]引入栅格环境下的障碍物占比作为修改权值的变量，对A^*算法的代价函数进行优化，同时结合DWA实现了简单环境下的实时避障，算法性能较单一算法提升较大，但实验环境较为简单，只优化了A^*算法的代价函数，全局路径规划能力提升较小，未考虑A^*算法计算得出的节点可能被遮挡等特殊情况。文献[21]提出了一种基于改进A^*算法与DWA相融合的移动机器人导航算法，实现了基于全局最优的未知障碍物规避，算法逻辑清晰，但只通过引入安全距离和路径平滑处理对A^*算法进行改进，全局路径搜索能力提升较小，且未能解决局部路径规划算法丢失节点导致的“假死”问题。

针对上述问题，通过去冗余节点策略、邻域搜索方式改进、代价函数改进和路径平滑对A^*算法进行改进，将DWA与改进A^*算法融合，对路径长度、避障性能等进行优化，最后对机器人“假死”问题提出解决方案。

1.   全局路径规划A^*算法改进

A^*算法的代价函数为

式中：g（n）为路径代价函数，计算从当前节点n到初始点消耗的代价；h（n）为启发函数，计算从当前节点n到目标点的最小代价评估值。

常见的启发函数有曼哈顿距离、切比雪夫距离和欧几里得距离，3种启发函数有不同的定义和应用场景。采用欧几里得距离作为启发函数时，A^*算法在缩短路径长度和规划时间、减少路径节点数等方面具有良好的效果。因此，本文采用欧几里得距离作为启发函数。

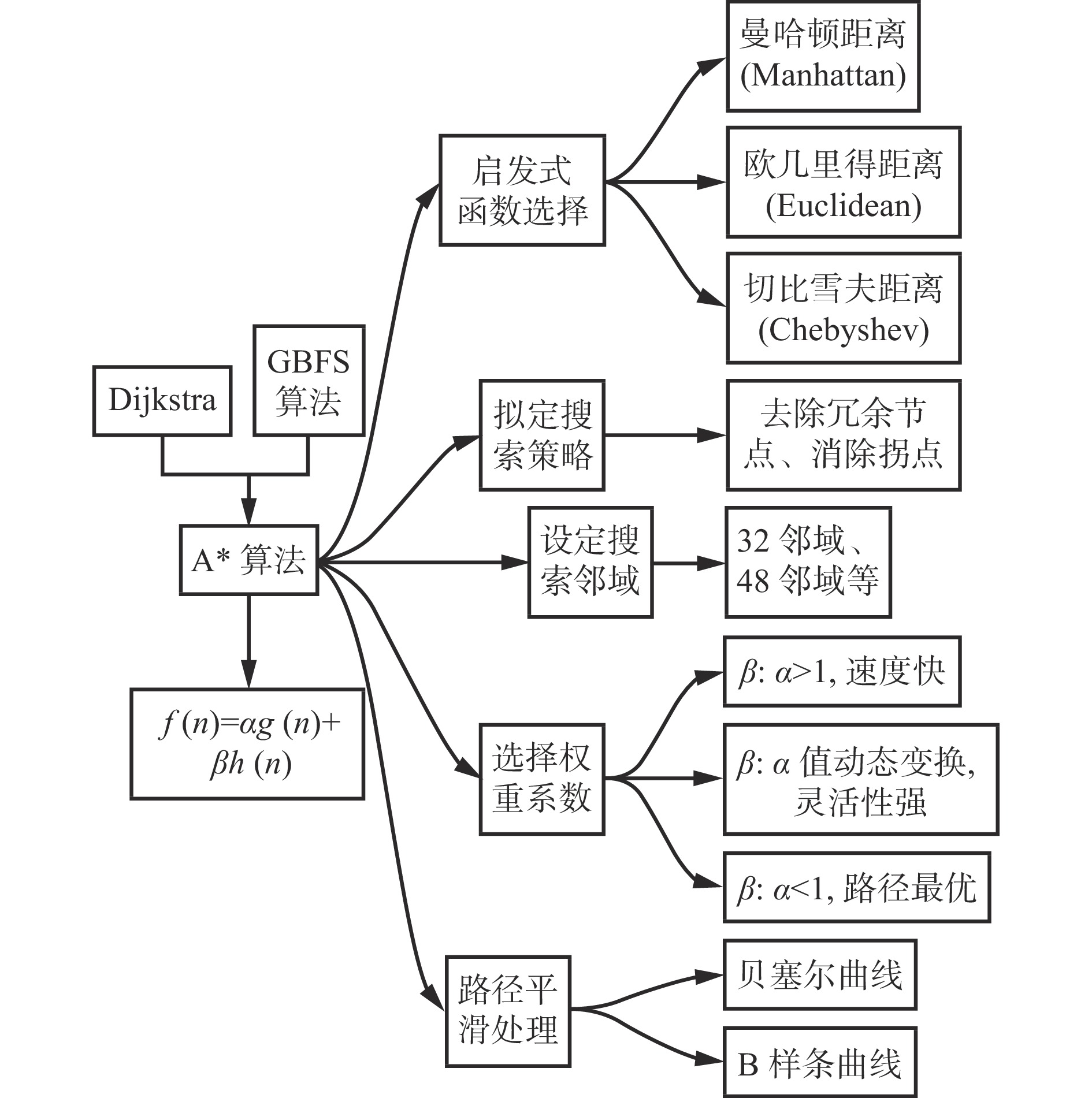
A^*算法改进途径如图1所示。通过去冗余节点策略、邻域搜索方式改进、代价函数改进和路径平滑对A^*算法进行改进。

图  1  A^*算法改进途径

Figure  1.  A^* algorithm improvement approach

下载: 全尺寸图片 幻灯片

1.1   去冗余节点策略

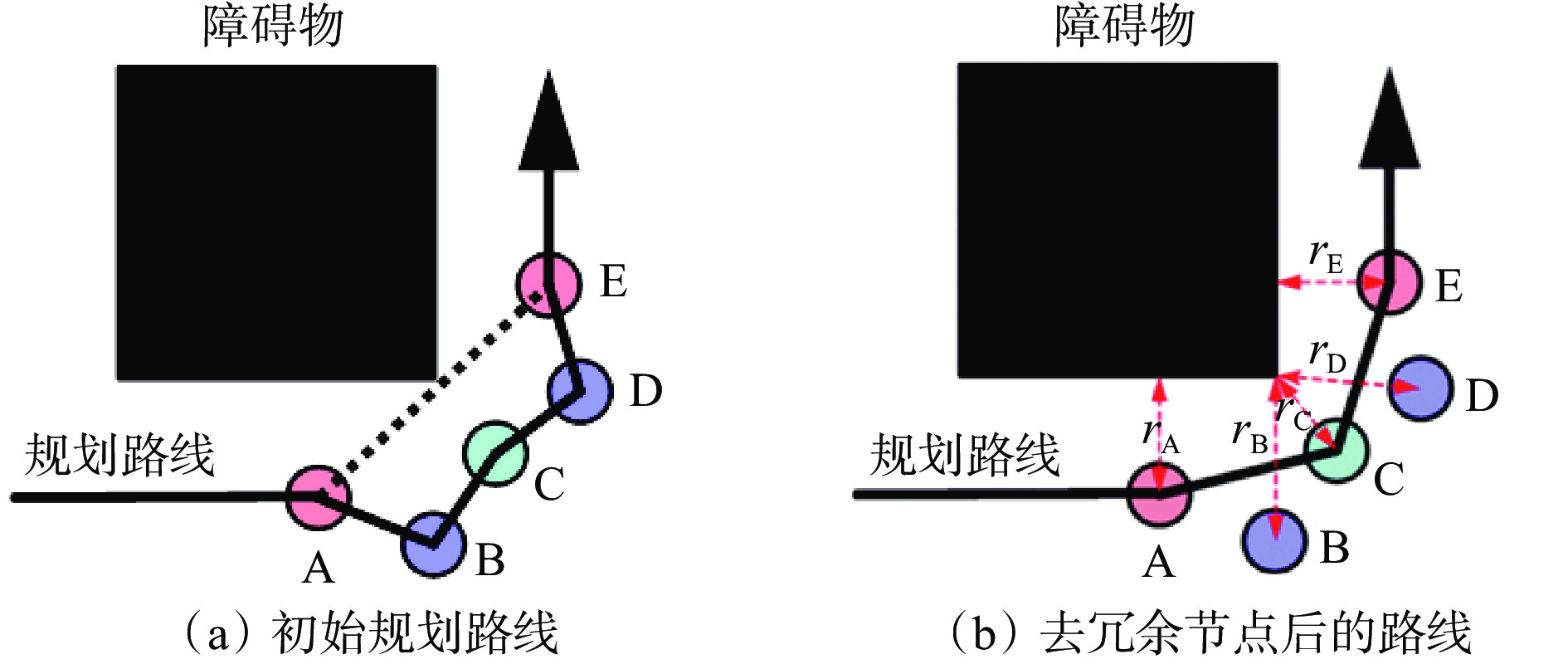
传统A^*算法规划出的路径由若干个节点连接而成，保留下的关键节点存在一定冗余，路径规划精度有进一步优化的空间。

去冗余节点策略如图2所示。传统A^*算法规划出的路径为A−B−C−D−E，但A−E路线最短，由于真实环境下需要考虑机器人机体大小，沿A−E路线行走会出现碰撞障碍物的危险。为保证机器人安全的前提下尽可能寻找最短路径，提出去冗余节点策略。设定一个安全距离$ r $，节点$ n $与最近障碍物的距离为$ {r_n} $，将其与安全距离$ r $进行比较：当$ {r_n} \leqslant r $时，保留节点$ n $；当$ {r_n} ＞ r $时，删除节点$ n $。若存在3个节点位于1条直线上的情况，说明中间节点是非必要节点，可以进一步删除。采取去冗余节点策略后，原路线改变为A−C−E，如图2（b）所示。去冗余节点策略既保证了机器人的安全运行，又缩短了路径长度。

图  2  去冗余节点策略

Figure  2.  Redundant node removal strategy

下载: 全尺寸图片 幻灯片

1.2   邻域搜索方式改进

传统A^*算法采用八邻域搜索方式，如图3所示，蓝色方块为搜索目标点，红色方块为初始点，箭头代表由初始点向外搜索的方向。通过计算代价函数找出距离目标点代价最小的邻域，作为下一个出发点，依此类推，直到到达目标点。八邻域搜索方式在没有搜索意义的方向造成了大量性能浪费，搜索效率低。

图  3  八邻域搜索方式

Figure  3.  Eight neighborhood search method

下载: 全尺寸图片 幻灯片

为提高搜索效率，针对不同工作环境，应适当调整远离目标点方向的搜索范围，在没有必要进行搜索的方向及时停止搜索，以释放计算资源。在输入目标点后，可修改搜索邻域进行算法简化，设“初始点−目标点”连线与水平方向的夹角为$\theta $，当$\theta $满足一定条件时，删除对应邻域。邻域删除策略见表1。

表  1  邻域删除策略

Table  1.  Neighborhood deletion strategy

角度区间	删除邻域
−22.5°≤θ＜22.5°	出发点左侧邻域
22.5°≤θ＜67.5°	出发点左下侧邻域
67.5°≤θ＜112.5°	出发点下侧邻域
112.5°≤θ＜157.5°	出发点右下侧邻域
−180°≤θ＜−157.5° 或 157.5°≤θ＜180°	出发点右侧邻域
−157.5°≤θ＜−112.5°	出发点右上侧邻域
−112.5°≤θ＜−67.5°	出发点上侧邻域
−67.5°≤θ＜−22.5°	出发点左上侧邻域

下载: 导出CSV 

| 显示表格

1.3   代价函数改进

在A^*算法的代价函数中，启发函数$ h\left( n \right) $所占权值默认为1。启发函数的权值大小影响路径搜索速度，权值越大，搜索速度越快，但搜索精度会随之下降。为了进一步加快算法的计算速度，定义启发函数的权值为一个变量，随着机器人与目标点间距离的变化而实时改变。在开始寻路阶段，目标点距离机器人较远，适当加快搜索速度，舍弃一些精度；靠近目标点时，降低搜索速度，寻找出最合适的通行路径。改进后的代价函数为

式中：$ d_{\mathrm{all}} $为初始点到目标点的欧几里得距离；$ d_{\mathrm{now}} $为当前节点到目标点的欧几里得距离；$ \left( {x_{\mathrm{g}},y_{\mathrm{g}}} \right) $为目标点坐标；$ \left( {x_n,y_n} \right) $为当前节点坐标；$ \left( {x_{\mathrm{s}},y_{\mathrm{s}}} \right) $为起点坐标。

在开始阶段，搜索速度非常快，随着路径规划推进，$ {{d_{\mathrm{now}}}/ {d_{\mathrm{all}}}} $的值越来越小，启发函数$ h\left( n \right) $的权值就越小，最终在到达目标点附近时启发函数的权值变得很小，此时搜索速度慢但搜索精度高，从而规划出安全路线并平稳到达目标点。

1.4   路径平滑

改进A^*算法规划出的路径是由初始点、必要转折点、目标点连接而成的折线，为使路线更符合机器人实际行走的路线，避免较多拐点，本文采用二阶贝塞尔曲线平滑路径。将改进A^*算法所得路径节点作为贝塞尔曲线的端点，即可实现最终规划路径的平滑处理。

2.   改进A^*算法与DWA融合

全局路径规划算法使得机器人能够快速获得一条由初始点到目标点的最优路径，但在运行过程中可能会出现新增障碍物，因此需要加入局部路径规划算法。

DWA的代价函数为

式中：$ {{H}}\left( {{v_i},{w_i}} \right) $为方位角评价函数，用来评价机器人行驶方向与目标所在方向的差值，差值越小，评价越高；$ {{J}}\left( {{v_i},{w_i}} \right) $为距离评价函数，评价机器人当前位置与附近障碍物位置的距离，距离越远，评价越高；$ {{V}}\left( {{v_i},{w_i}} \right) $为速度评价函数，评价机器人当前的线速度，速度越快，评价越高。

传统的DWA融合了3个评价函数，且权值比例为1∶1∶1，可实现近距离、障碍物较少环境下的避障，但只模拟并评价下一时刻的最优轨迹，遇到“U”型障碍不能很好地避障。修改代价函数的权值可影响局部避障效果，因此在不同应用环境下应对应不同的权值。

将DWA与改进后的A^*算法进行算法融合，DWA可弥补A^*算法无法进行实时避障的不足，同时A^*算法能够规划出远距离最优路径，有效避免DWA无法进行长远距离避障的问题。具体融合策略：将改进A^*算法规划出的路径节点依次作为DWA的局部目标点，即将全局规划路径拆分为多段能够实现避障的局部规划路径，每当机器人抵达一个全局路径规划节点时，以当前节点作为DWA的出发点，下一个节点作为DWA的目标点，紧接着进行下一段路径的行走，依此类推，直到机器人抵达最终目标点。

由于DWA具有避障能力，决定融合算法全局路径规划能力的改进A^*算法可在此基础上进一步优化，只要相隔节点之间的连线不经过障碍物区域，即可删除中间节点，如图2中路线A−C−E可进一步优化为A−E，这时不需要考虑实际环境下的碰撞问题，在靠近障碍物时，DWA会控制机器人进行对应的位姿调整。这样规划出的路径长度更短、节点更少、规划速度更快、轨迹更平滑。

3.   “假死”应对方案

融合算法寻找路径效率更高，但遇到新增障碍物的情况时，仍无法继续寻找路径，具体情况如下：① 当存在“L”型和“U”型障碍物或障碍物密集时，机器人很容易陷入“假死”状态，这也是所有与DWA融合的算法的共同问题。② 新增的障碍物覆盖了A^*算法规划出的路径节点，机器人丢失局部目标点，这也是所有与A^*算法融合的算法的共同问题。

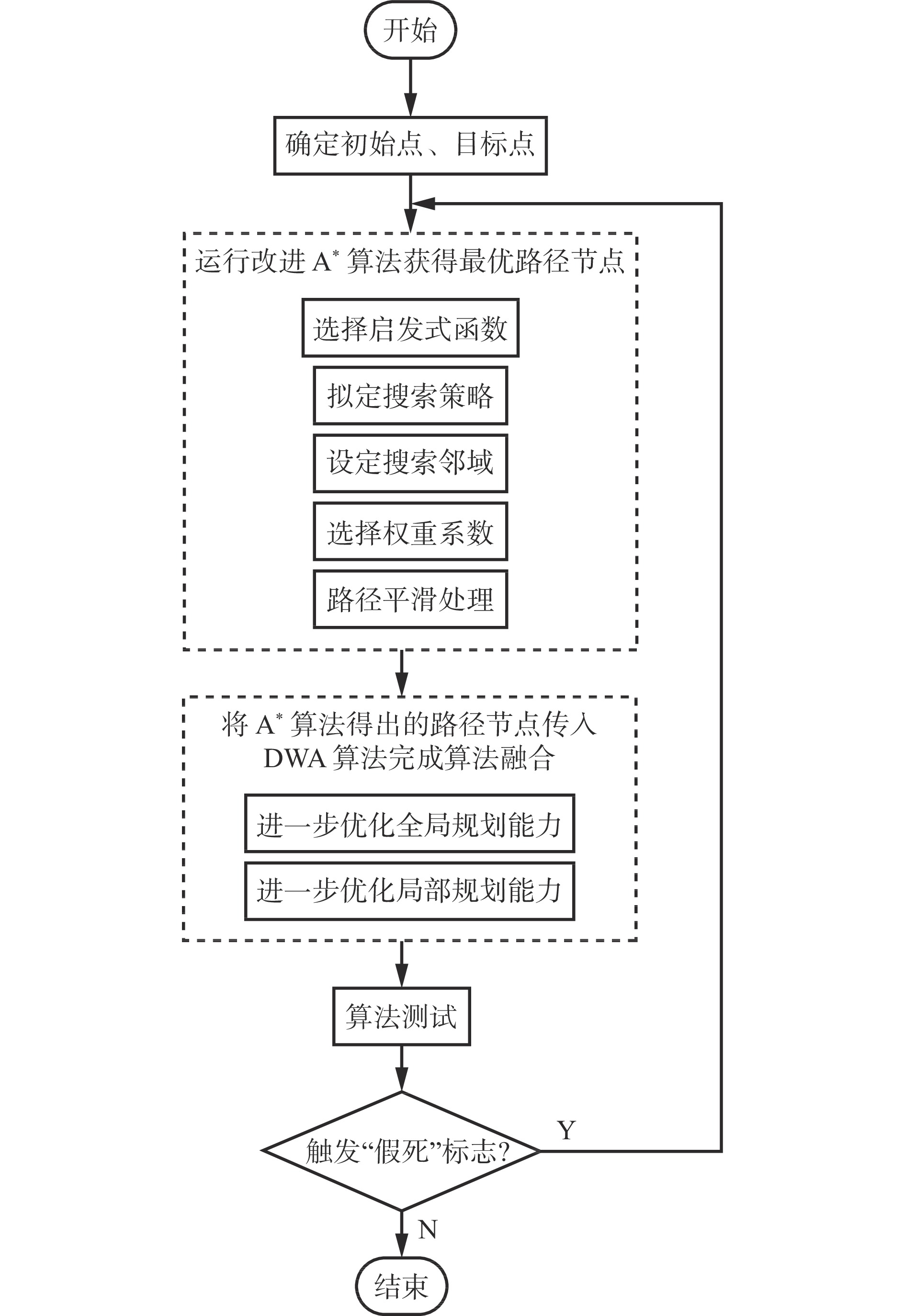
为解决上述问题，以当前初始点为起点，再次调用融合算法，即重新进行全局路径规划，将得到的新节点代替原有的局部目标点，按照新路线进行后续工作。设定一个“假死”标志，再次调用融合算法。“假死”状态：① 在规定时间内没有实现目标点的更迭。② 机器人速度降低至某一阈值，但所处位置不是终点。

机器人行走方案流程如图4所示。

图  4  机器人行走方案流程

Figure  4.  Robot walking plan flow

下载: 全尺寸图片 幻灯片

4.   仿真分析

4.1   改进A^*算法性能验证

采用PyCharm2021.3.3软件作为仿真平台，记录算法计算的时间、路径长度、节点数等参数。足式机器人仅需要离散落足点即可完成任务，因此建立离散地图，设机器人半径为1 cm。改进A^*算法仿真结果如图5所示。

图  5  改进A^*算法仿真结果

Figure  5.  Improved A^* algorithm simulation results

下载: 全尺寸图片 幻灯片

A^*算法改进前后性能对比见表2。在保证机器人行走安全稳定的基础上，改进A^*算法较传统A^*算法的计算时间缩短了65%，路径长度缩短了24.1%，路径节点数量减少了27.65%，最终得出的路径更为平滑。

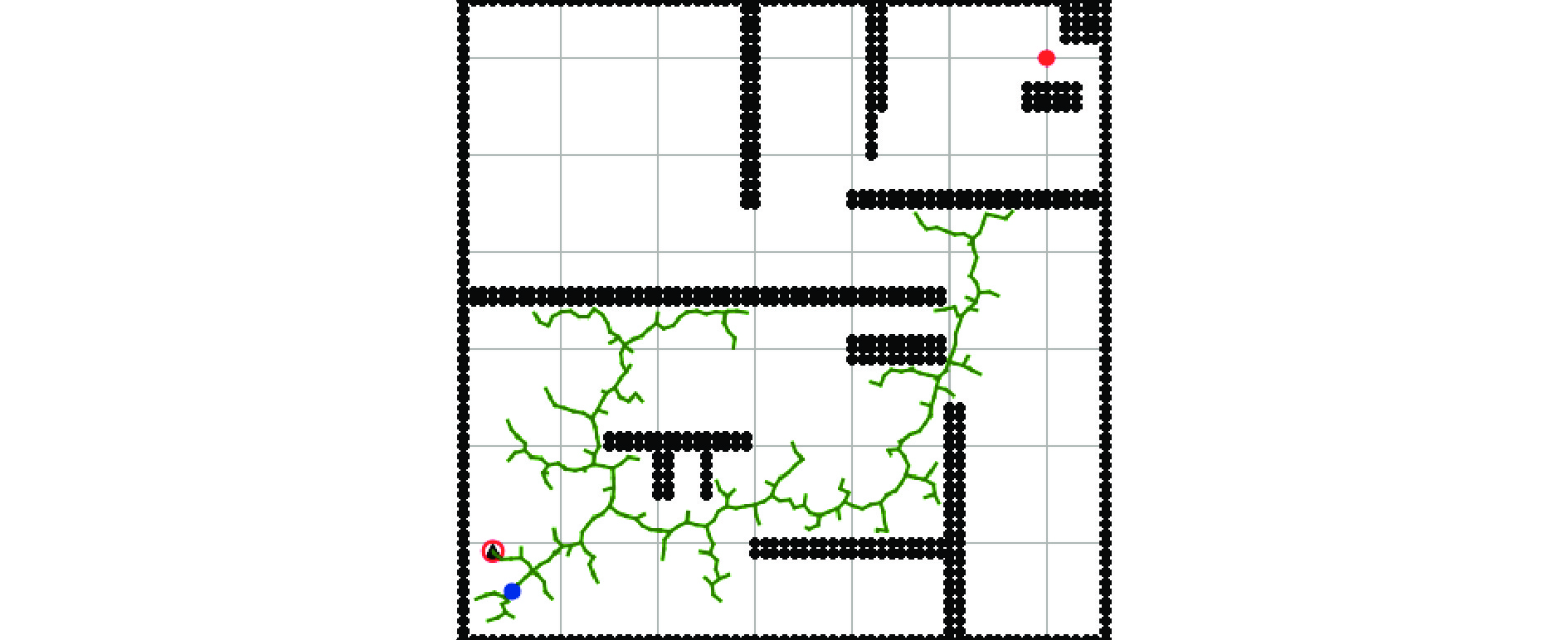
表  2  A^*算法改进前后性能对比

Table  2.  Comparison of performance before and after A^* algorithm improvement

算法	规划时间/s	规划路径长度/cm	路径节点数/个
传统A*算法	1.20	55.6	47
应用去冗余节点	1.19	38.8	31
改进A*算法	0.42	42.2	34

下载: 导出CSV 

| 显示表格

作为对照，在同一地图环境下采用RRT算法进行对比测试，由于地图中障碍物密集，狭窄通道较多，采用RRT算法并未得到最终路径，如图6所示，绿色纹路代表RRT算法搜索的区域。

图  6  RRT算法路径规划结果

Figure  6.  RRT algorithm path planning results

下载: 全尺寸图片 幻灯片

4.2   融合算法性能验证

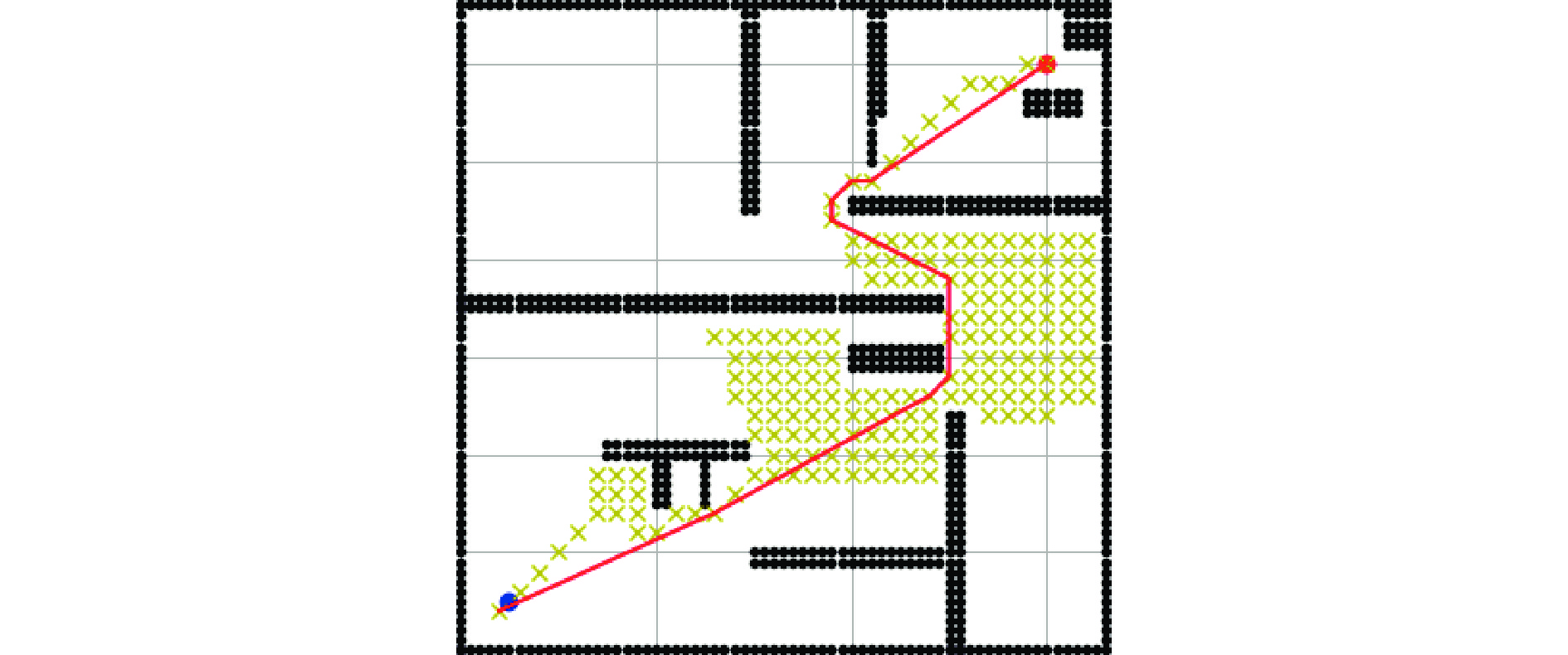
融合算法路径规划结果如图7所示。优化后的路径长度为41.4 cm，规划时间为0.40 s，路径节点数为10个。与传统A^*算法相比，融合算法的运算效率、搜索精度大幅提高，规划路径缩短了25.54%，运算时间减少了2/3，路径节点数大幅减少。

图  7  融合算法路径规划结果

Figure  7.  Fusion algorithm path planning results

下载: 全尺寸图片 幻灯片

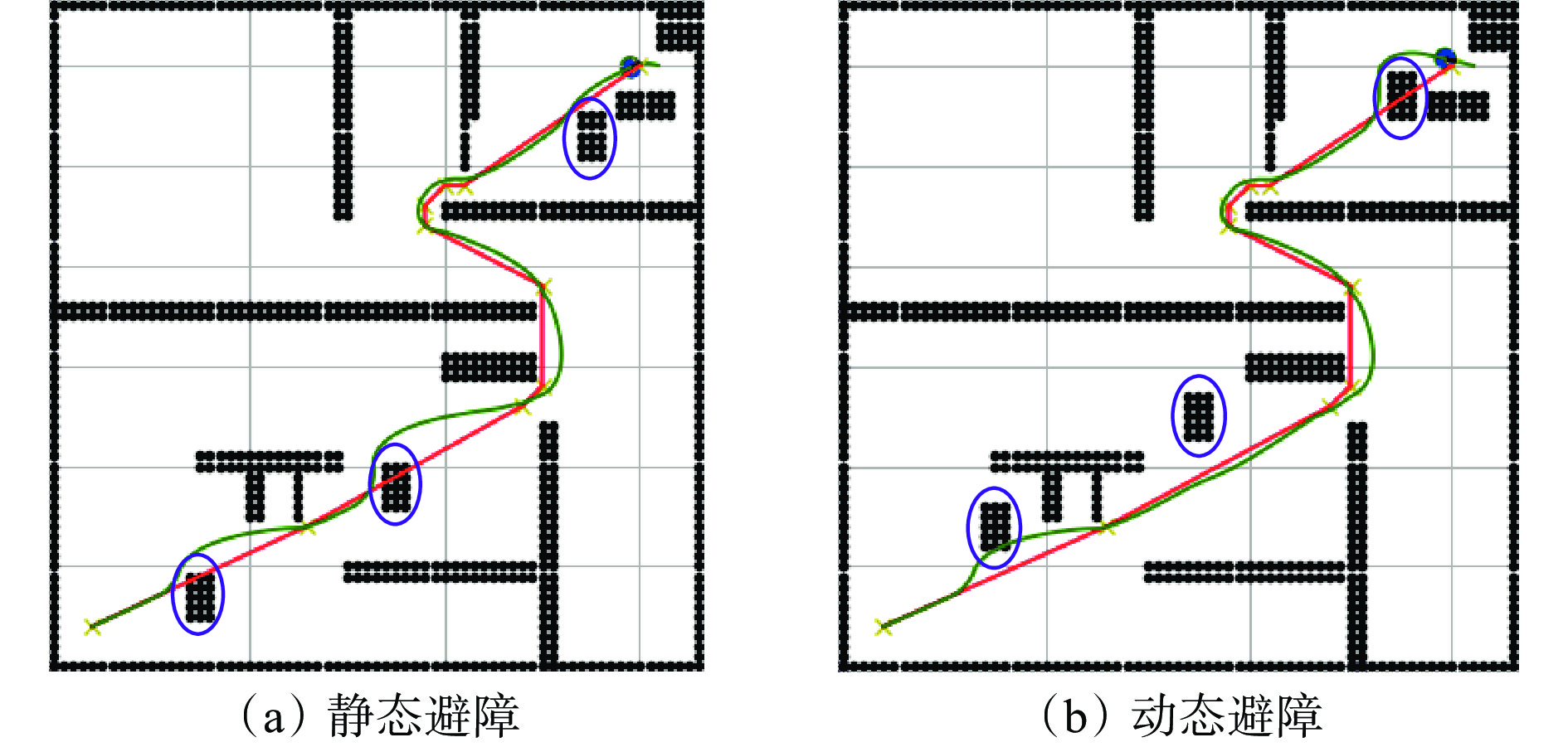
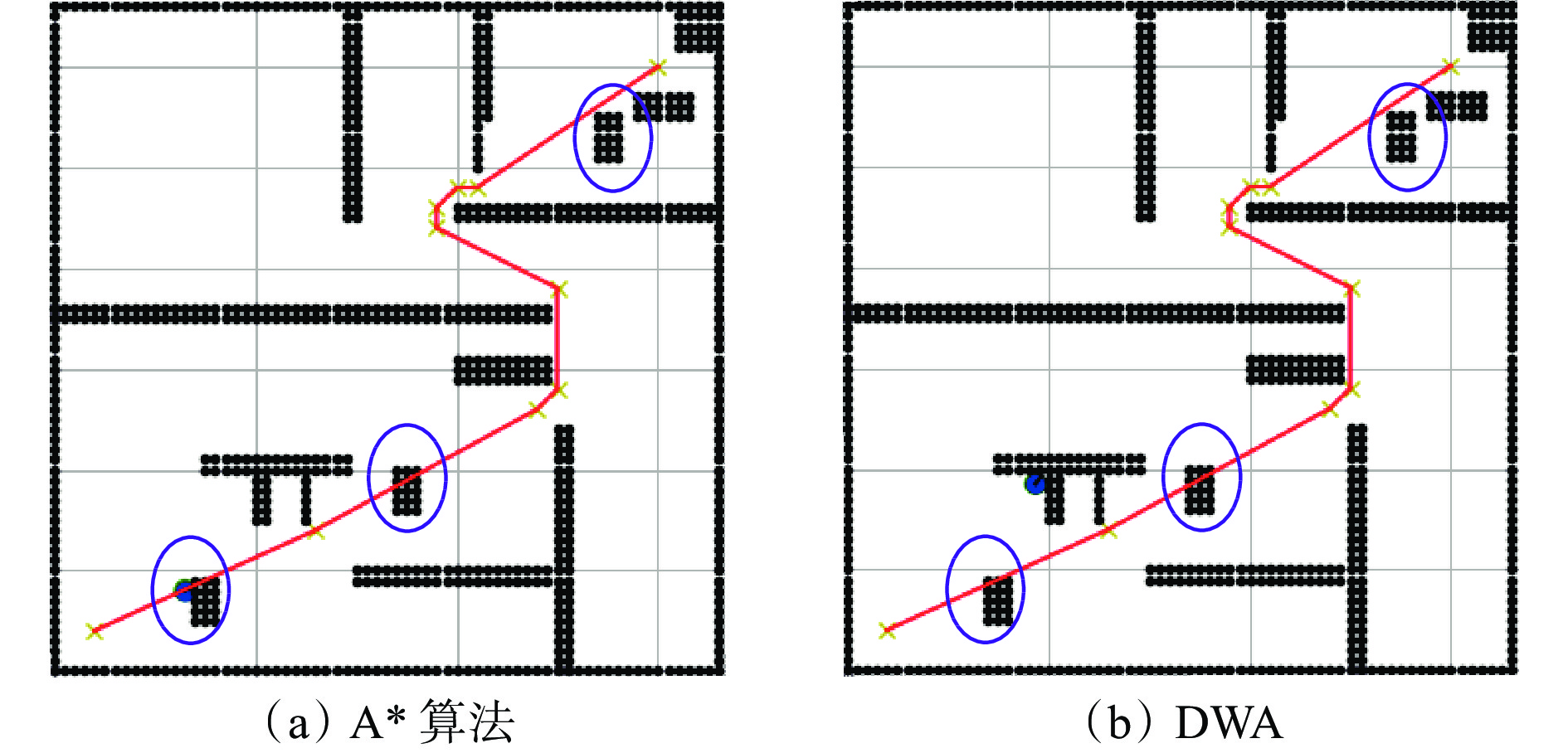
在多节点、多障碍物环境下，保持仿真参数不变，新增动态障碍物和静态障碍物，分别进行仿真研究，结果如图8所示，图中紫色圆圈包围的障碍物为新增障碍物。可看出，面对路径上突然出现的未知障碍物，在局部路径规划算法的作用下，机器人临时改变速度参数和行走方向，成功绕开障碍继续行走，最终路线为图中的绿色曲线。单一的路径规划算法无法实现这一要求，如图9所示。

图  8  融合算法避障性能验证

Figure  8.  Verification of obstacle avoidance performance of fusion algorithm

下载: 全尺寸图片 幻灯片

图  9  单一路径规划算法避障性能

Figure  9.  Obstacle avoidance performance of single path planning algorithm

下载: 全尺寸图片 幻灯片

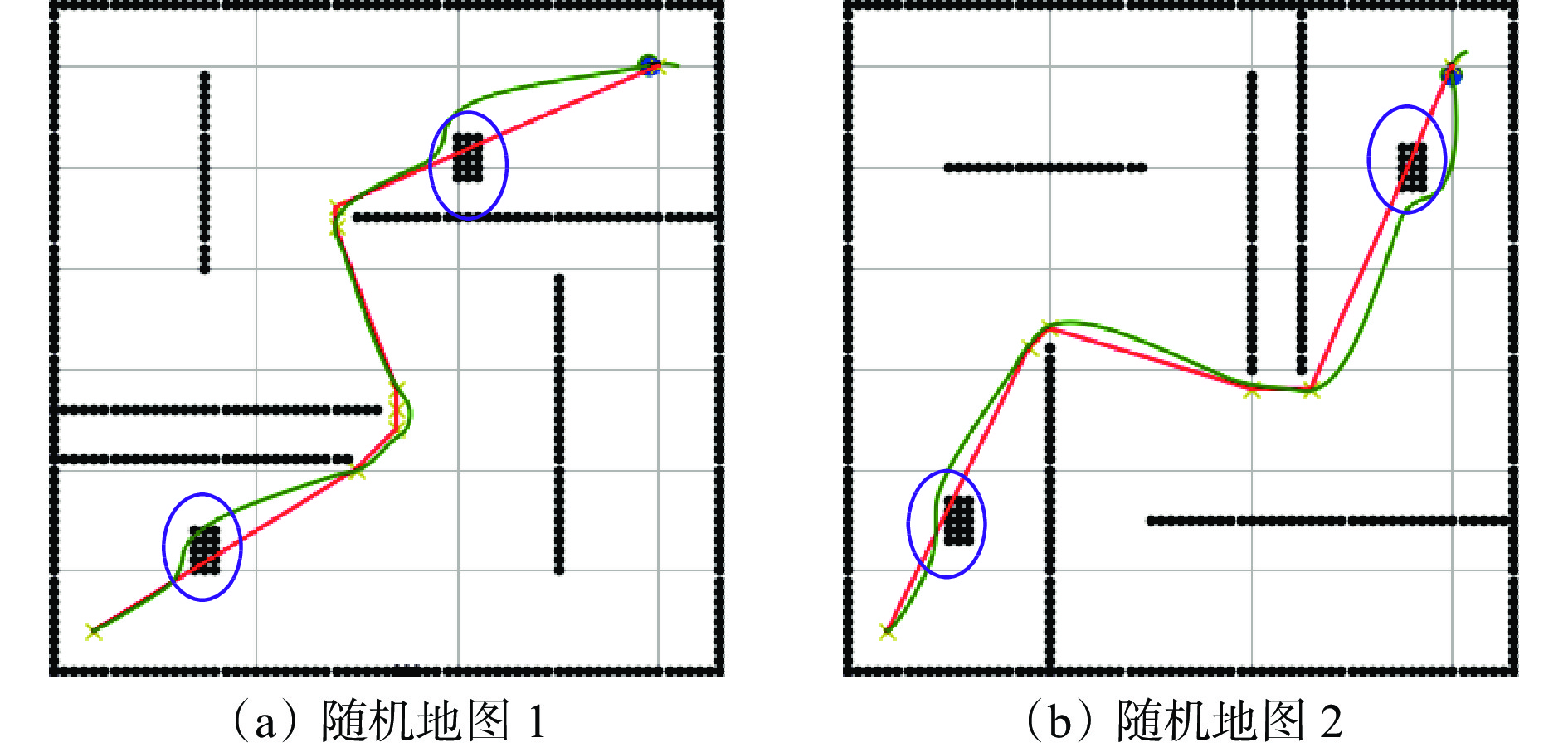
为进一步验证融合算法的优越性，设置多个随机地图进行重复测试，结果如图10所示。可看出融合算法能够在随机地图内规划出路径并顺利抵达终点。

图  10  融合算法在随机地图上的测试结果

Figure  10.  Test results of fusion algorithm on random maps

下载: 全尺寸图片 幻灯片

4.3   “假死”应对方案验证

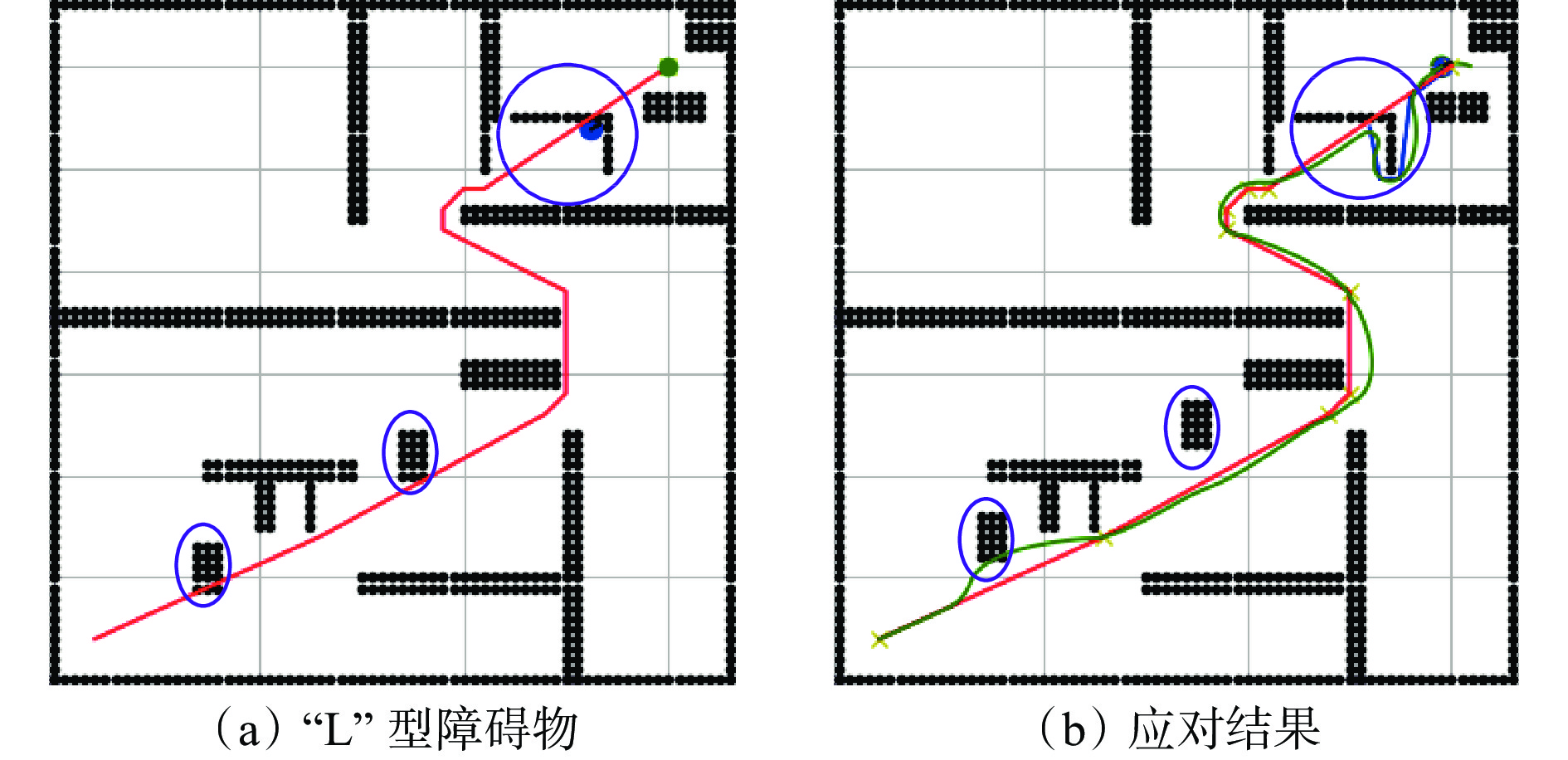
以机器人遇到“L”型障碍物为例，路径规划结果如图11所示。机器人进入了“假死”状态，无法到达下一个目标点，这时调用融合算法修正路径。机器人在“假死”位置重新进行全局路径规划，更新了行走路径，成功到达最终目标点。

图  11  “假死”应对方案路径规划结果

Figure  11.  Path planning results of the response plan for "feigned death"

下载: 全尺寸图片 幻灯片

仿真结果表明，融合算法能够实现机器人在复杂地形下快速寻路、避障，同时解决遇到特殊新增障碍物时无法继续寻找路径的问题，提高了足式机器人适应复杂环境的能力。

5.   实机实验

使用JetHexa六足机器人进行路径规划算法有效性验证实验，实验地图环境如图12所示。设置多个障碍，代表井下环境中的墙面、巷道、大型物体等，静态障碍物视为掉落的大块煤块等，动态障碍物视为地面上滚动的煤块或移动器械等，绿色“×”标记代表目标位置，初始点即为机器人所在位置。

图  12  实验地图环境

Figure  12.  Experimental map environment

下载: 全尺寸图片 幻灯片

通过机器人操作系统（Robot Operating System，ROS）完成建图及地图保存工作，如图13所示。

图  13  地图构建

Figure  13.  Map construction

下载: 全尺寸图片 幻灯片

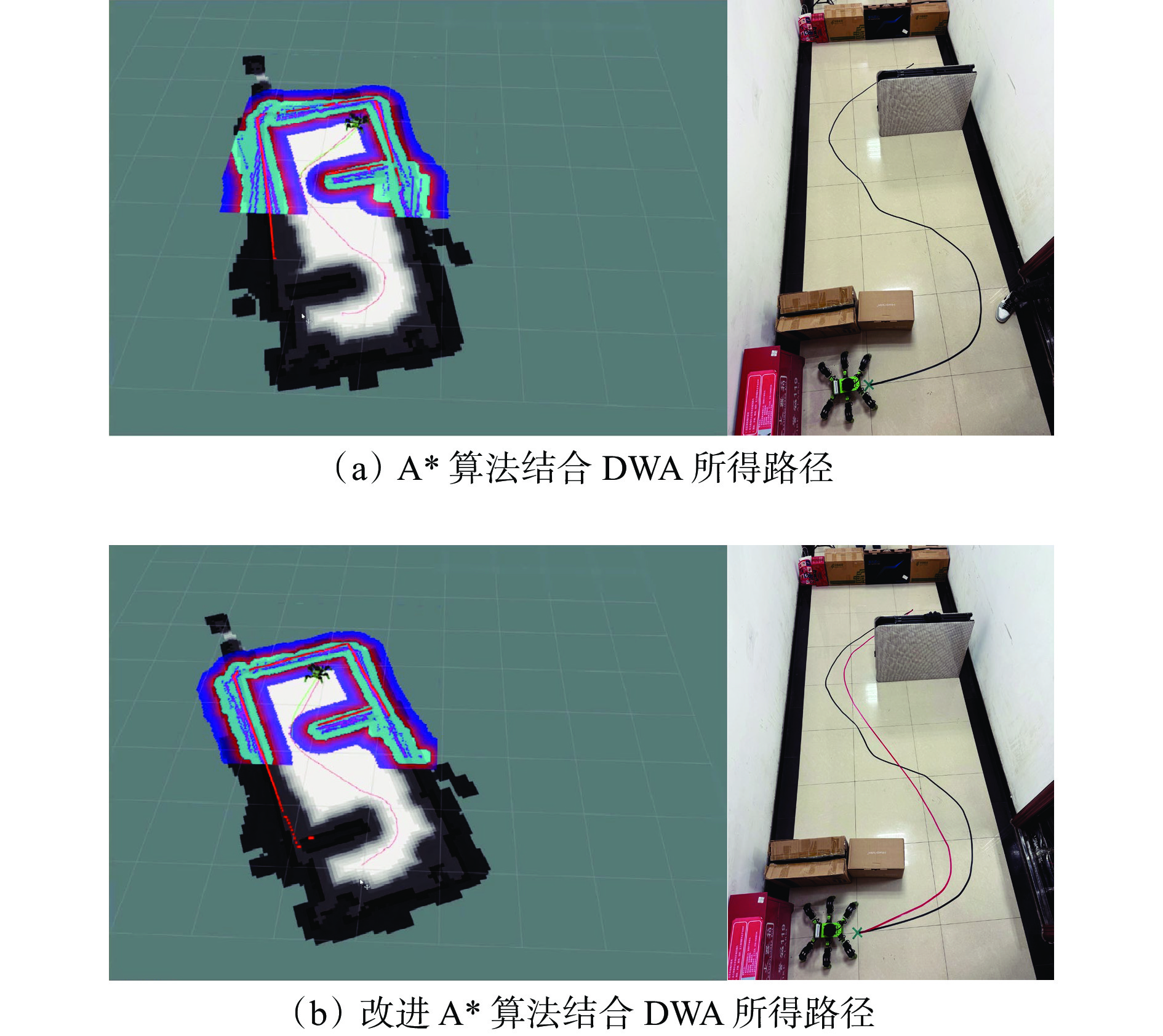
算法改进前后路径规划结果如图14所示，路径长度和规划时间对比结果见表3。由表3可得，融合算法规划速度更快、规划出的路径更短。

图  14  算法改进前后路径规划结果

Figure  14.  Path planning results before and after algorithm improvement

下载: 全尺寸图片 幻灯片

表  3  算法改进前后性能对比

Table  3.  Comparison of performance before and after algorithm improvement

算法	规划时间/s	路径长度/cm
A*算法+DWA	1.97	424
改进A*算法+DWA	1.10	368

下载: 导出CSV 

| 显示表格

在规划好的路径上放置静态、动态障碍物（通过人来回行走扮演），采用融合算法后，机器人顺利完成避障任务，如图15所示。可看出融合算法具备对静态、动态障碍物的避障能力，验证了融合算法的有效性和优越性。

图  15  融合算法避障性能验证

Figure  15.  Verification of obstacle avoidance performance of fusion algorithm

下载: 全尺寸图片 幻灯片

6.   结论

1） 针对传统A^*算法在计算效率、路径搜索精度上的不足，通过去冗余节点策略、邻域搜索方式改进、代价函数改进和路径平滑对A^*算法进行改进。改进A^*算法较传统A^*算法的计算时间缩短了65%，路径长度缩短了24.1%，路径节点数量减少了27.65%，最终得出的路径更为平滑。

2） 将改进A^*算法和DWA进行融合，进一步提升了全局路径规划能力及在多障碍物环境下的动态和静态避障能力。

3） 针对机器人在特殊新增障碍物环境下无法继续行走从而进入“假死”状态的问题，设计“假死”标志并二次调用融合算法，及时更新工作路径，保证了工作效率。

4） 模拟煤矿井下环境进行实机实验，验证了融合算法的有效性和优越性。