Research on the deformation and failure depth of the floor in fully mechanized top coal caving of extra-thick seam
-
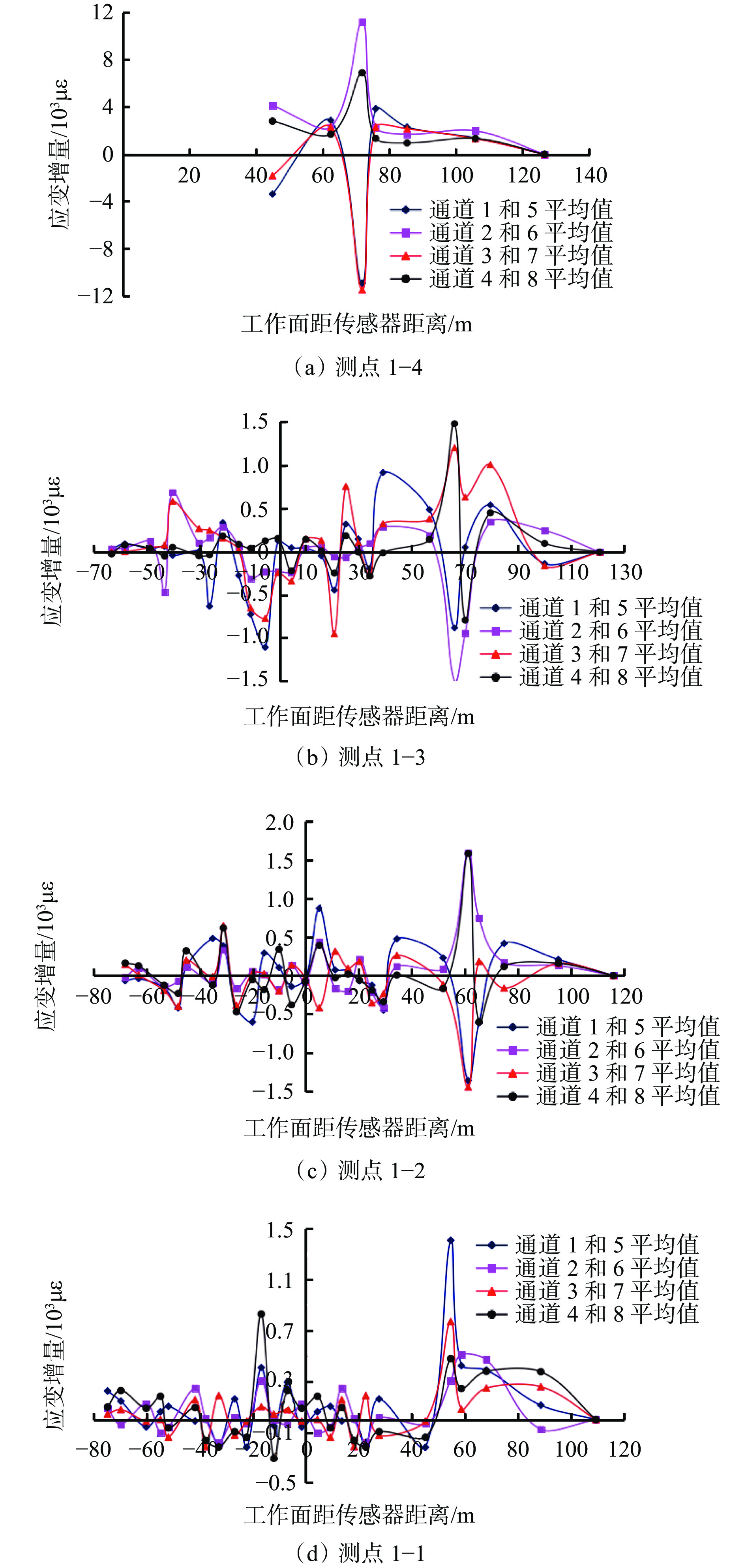
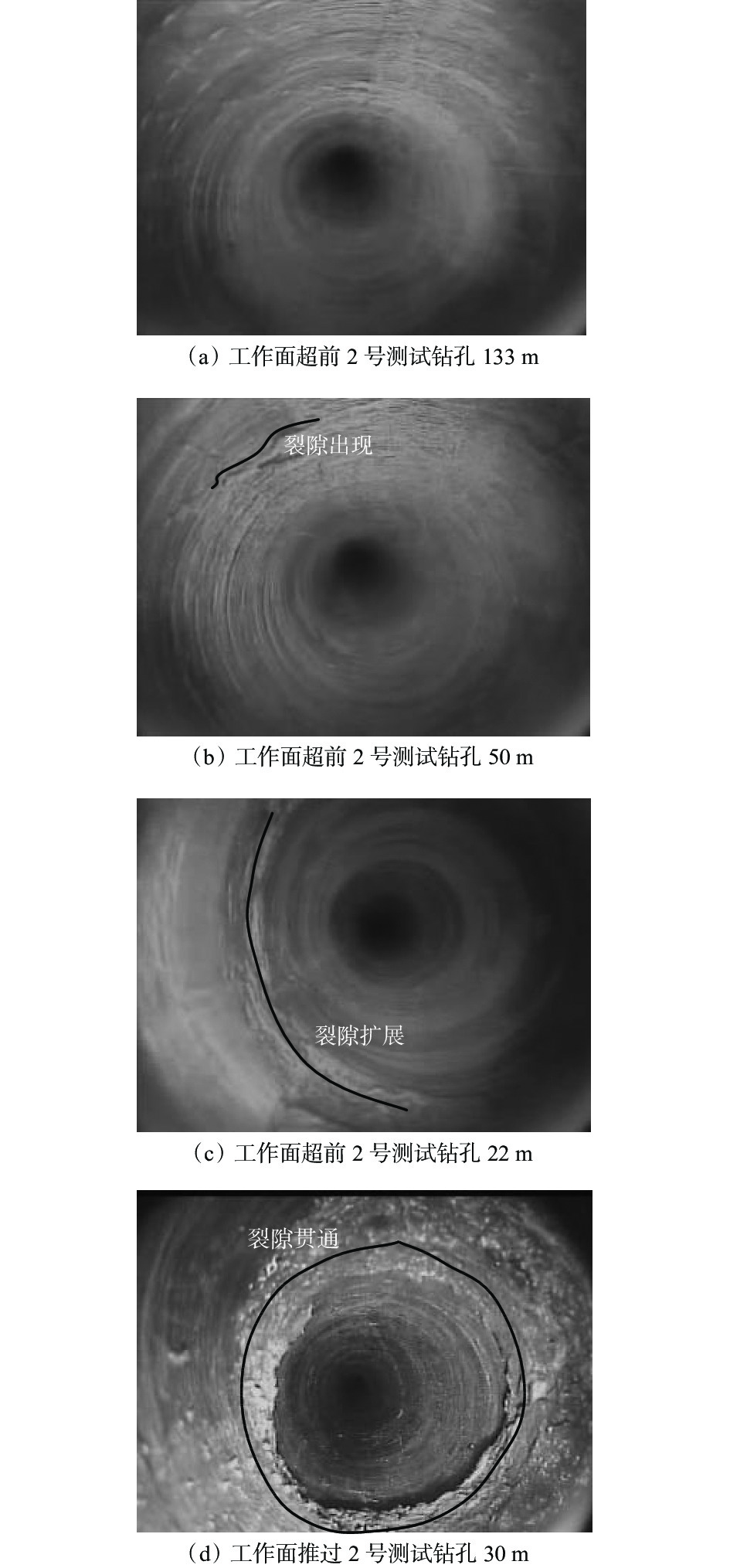
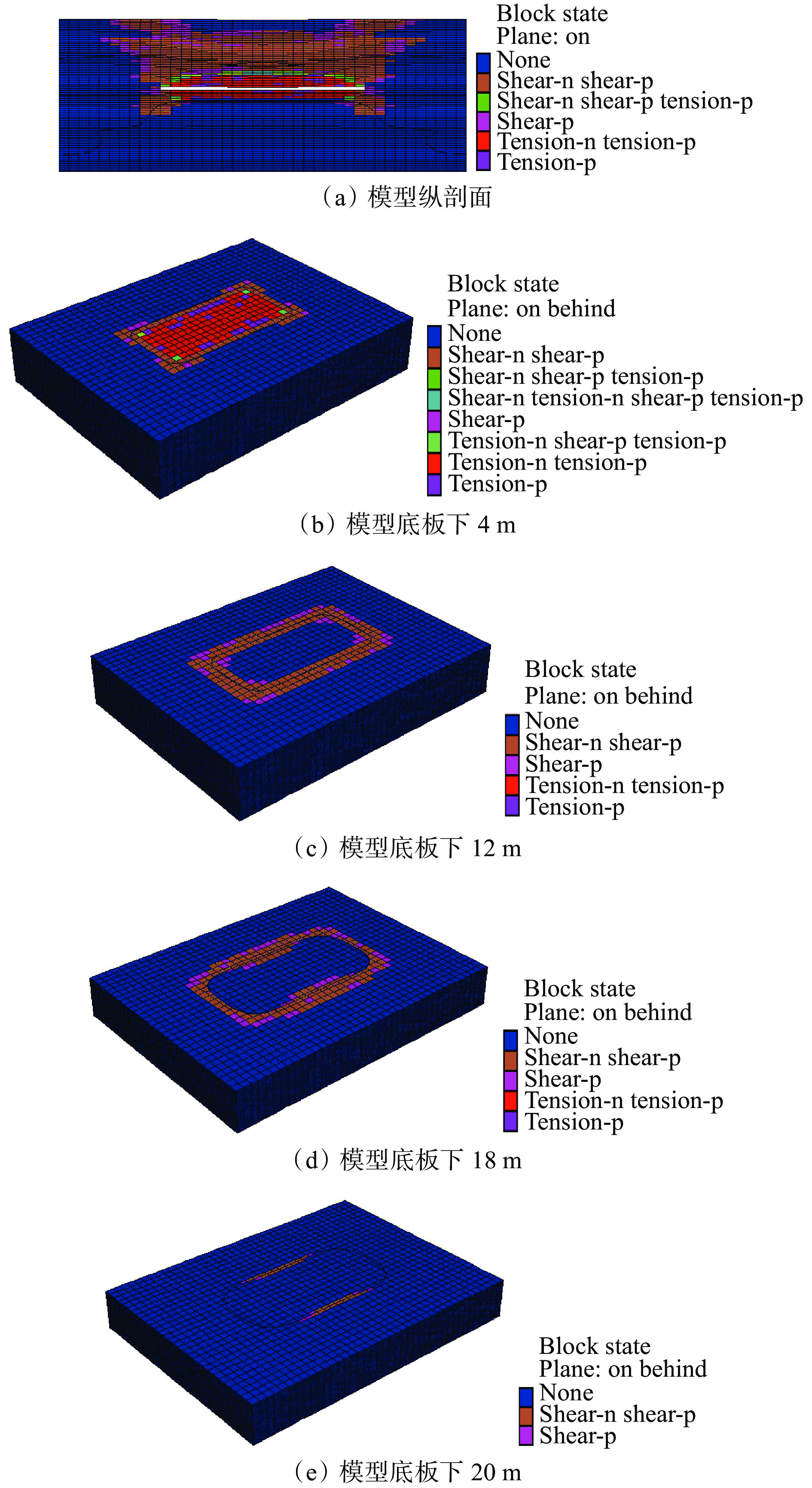
摘要: 为探究特厚煤层综放开采条件下底板变形破坏深度，以兖矿能源集团股份有限公司东滩煤矿1305工作面为背景，采用现场实测、数值模拟和理论计算等方法综合分析了该工作面采动煤层底板变形破坏深度。采用应变感应法和钻孔成像技术的现场实测结果表明：底板受采动矿压作用在水平和垂直方向上存在明显的显现特征，水平方向上超前测点50 m附近、底板浅部10 m深度位置开始受采动矿压影响，工作面推过一定距离之后底板变形破坏剧烈；底板不同深度水平方向上超前距和滞后距变化范围分别为96～115 m和48～52 m，工作面综放开采底板变形破坏深度为16~20 m，垂深20 m以下底板岩层以弹性变形为主。数值模拟的底板不同深度塑性区分布特征表明，随着距工作面底板距离越远，受采动矿压影响越小，塑性区范围越小，底板下20 m基本没发生破坏。理论计算结果确定了底板变形破坏深度为19.2 m。综合现场实测、数值模拟和理论计算结果，可知1305工作面综放开采底板变形破坏深度不超过20 m。研究结果可为矿井特厚煤层综放开采底板水害防治提供量化依据。Abstract: In order to explore the deformation and failure depth of the floor under the condition of fully mechanized top coal caving of extra-thick coal seam, this paper takes 1305 working face of Dongtan Coal Mine of Yankuang Energy Group Co., Ltd. as the background. The deformation and failure depth of the floor in the mining coal seam of the working face is comprehensively analyzed by using field measurement, numerical simulation and theoretical calculation. The field measurement results using the strain induction method and borehole imaging technology show the following results. The floor is affected by mining ground pressure, and there are obvious characteristics in horizontal and vertical directions. In the horizontal direction, the position near the advanced support measuring point of 50 m and at the depth of 10 m in the shallow part of the floor starts to be affected by the mining ground pressure. After the working face is pushed over a certain distance, the deformation and failure of the floor are severe. The variation range of crossover distance and lag distance in the horizontal direction of different depths of the floor is 96-115 m and 48-52 m respectively. The deformation and failure depth of the floor in fully mechanized top coal caving of the working face is 16-20 m. The floor rock below the vertical depth of 20 m is mainly elastic deformation. The distribution characteristics of the plastic zone in different depths of the floor by numerical simulation show that the farther the distance from the working face floor is, the smaller the influence of mining pressure is, and the smaller the range of the plastic zone is. The 20 m under the floor is basically not damaged. The result of the theoretical calculation confirms that the deformation and failure depth of the floor is 19.2 m. Based on the results of field measurement, numerical simulation and theoretical calculation, the deformation and failure depth of the floor in 1305 working face is less than 20 m. The research results can provide the quantitative basis for the prevention and control of floor water disasters in fully mechanized top coal caving of extra-thick coal seams.
-
0. 引言
煤矿智能化是煤炭工业高质量发展的核心技术支撑，大力推广应用煤矿机器人，推进机械化换人、自动化减人和智能装备替代高危岗位作业已成为国家煤炭能源发展战略和煤炭行业共识[1-3]。煤矿机器人的自主移动是智能化发展的必然方向，路径规划是实现机器人自主移动的前提和基础，是煤矿机器人的关键核心技术之一[4-6]。
路径规划是指在起点和终点已知的情况下，寻找一条可通行、无碰撞路径的过程。国内外学者已经开展了大量的煤矿井下路径规划研究工作。田子建等[7]将相对速度场和相对加速度场引入势场函数中，提出了基于全局势场线的局部路径规划算法。Gao Yongxin等[8]将多目标优化算法和模糊控制算法结合，提出了一种新的混合优化算法来解决煤矿巡逻机器人的路径规划问题。Song Baoye等[9]研究了基于改进蚁群优化算法的煤矿机器人路径规划方法，可有效减少路径规划时间和提高路径规划质量。陶德俊等[10]基于改进的A*算法为煤矿救援机器人规划平滑路径，采用动态规划（Dynamic Programming，D−P）算法和三次样条函数拟合以减少路径转折点和长度。Mao Ruiqing等[11]基于Dijkstra和蚁群优化算法提出了一种煤矿机器人路径规划方法，改善了机器人的路径规划能力。鲍久圣等[12]针对无轨胶轮车井下无人驾驶的路径规划需求，对传统A*算法和人工势场法进行改进，改进算法的路径搜索时间缩短为传统算法的20%左右。煤矿井下路径规划多以传统A*算法、人工势场法和智能算法为主，取得了一定进展，但由于煤矿井下自由空间狭长局促，环境复杂多变，最优路径选取、路径规划效率和路径规划实时调整与避障等问题仍有待进一步深入研究。
相较于传统A*算法、人工势场法和智能算法，概率路线图（Probabilistic Road Map，PRM）算法具有可动态更新路径、计算量小、算法复杂度不依赖于地图复杂度、可避免对位姿空间精确定位等特点，更加适用于煤矿井下复杂动态环境。代嘉惠[13]采用传统PRM算法结合实际煤矿井下环境地图，规划出适合煤矿救援机器人自主移动的行走路线，但存在采样的节点距离障碍物较近导致规划路径可通行性差的问题。金书奎等[14]基于巡检点坐标，使用传统PRM算法规划出适用于巡检机器人定点停留的全局路径，通过对障碍物进行膨胀，使规划的路径几乎处于道路中心位置，以防止机器人发生碰撞，但膨胀障碍物可能导致煤矿井下通行空间更加局促。田洪清等[15]将PRM算法与人工势场法进行融合，成功规划出满足复杂越野环境的高效可通行路径，但不适用于煤矿井下狭长局促空间。S. Sulaiman等[16]将D* Lite算法和基于几何的混合算法相结合，采用延迟PRM算法在配置空间中创建节点，但未考虑PRM算法难以保障节点均匀分布于自由空间中的问题。
针对上述问题，本文提出了一种基于改进PRM算法的煤矿机器人路径规划方法。在PRM算法中融合人工势场法，并利用D* Lite算法进行搜索得到最优路径，有效提高算法效率和路径的可通行性，当路径上出现障碍物时能够准确实现重规划，为煤矿井下机器人的路径规划提供有效的解决方案。
1. PRM算法原理
PRM是L. E. Kavraki等[17]提出的一种基于图的搜索算法，其实现可分为构造和查询2个阶段。在构造阶段，首先在构形空间C内进行采样，对采样的节点进行碰撞检测，并测试相邻节点间的连线是否经过障碍物，以构建概率地图$G = (V,E)$，其中V为自由空间中发布的节点c的集合，E为连接各节点的边集。在查询阶段，根据起始节点cs、目标节点cg的位置和构造阶段构建的概率地图G，将cs和cg连接到G中的节点，采用搜索算法从G中搜索可行路径。
PRM算法构造阶段伪代码如下。
Algorithm PRM算法构建无向图
repeat
c ← C空间中随机采样1个点；
if 碰撞检测后c不在自由空间中
将c加入图节点集合，即V ← V∪{c}；
N ← V中c的临近节点集； //N为临近节点集
for each c' in N //c '为N中的节点
if局部规划器能连接c和c'
将无向边（c，c'）加入图的边集合；
else
将c加入1个新的子图；
else计算c运动后的新节点c''
将c''加入图节点集合；
N ← c''的临近节点集；
for each c' in N
if局部规划器能连接c''和c'
将无向边（c''，c'）加入图的边集合；
else
将c''加入1个新的子图；
end
end
until满足终止条件
2. 改进PRM算法
2.1 基于人工势场法的概率地图构建
人工势场法是O. Khatib提出的实时避障算法[18]，其算法简洁、实时性较好且高效，被广泛应用于机器人路径规划领域。人工势场法基本思想：将机器人看作1个质点，在机器人运动的平面地图中设立虚拟势场，赋予目标节点与机器人相互吸引的力、障碍物与机器人相互排斥的力，通过二者作用于机器人上的合力，完成对机器人的运动控制。
引力势场${U_{\text{a}}}\left( {{c}} \right) $和引力${F_{\text{a}}}\left( {{c}} \right) $分别为
$$ {U_{\text{a}}}\left( {{c}} \right){\text{ = }}\frac{1}{2}\varepsilon {\rho ^2}\left( {{{c}},{c_{\rm{g}}}} \right) $$ (1) $$ {F_{\rm{a}}}\left( c \right) = - \nabla {U_{\rm{a}}}\left( c \right) = \varepsilon \rho \left( {c,{c_{\rm{g}}}} \right) $$ (2) 式中：ε为引力势场强度（正比例增益系数）；$\;\rho \left( {c,{c_{\rm{g}}}} \right)$为机器人当前节点c与目标节点cg之间的距离。
斥力势场${U_{\rm{r}}}\left( c \right)$和斥力${F_{\rm{r}}}\left( c \right)$分别为
$$ {U_{\rm{r}}}\left( c \right) = \left\{ \begin{gathered} \frac{1}{2}\delta {\left( {\frac{1}{{\rho \left( {c,{c_{{\rm{obs}}}}} \right)}} - \frac{1}{{{\rho _0}}}} \right)^2}\quad 0 \leqslant \rho \left( {c,{c_{{\rm{obs}}}}} \right) \leqslant {\rho _0} \\ 0\quad \rho \left( {c,{c_{{\rm{obs}}}}} \right) ＞ {\rho _0} \\ \end{gathered} \right. $$ (3) $$ {F_{\rm{r}}}\left( {\text{c}} \right) = - \nabla {U_{\rm{r}}}\left( c \right) $$ (4) 式中：δ为斥力势场强度（正比例增益系数）；ρ(c，cobs)为机器人当前节点c与障碍物节点cobs之间的距离；${\rho _0}$为障碍物与机器人之间保持的最大安全距离。
则总势能U和机器人所受合力F为
$$ U = {U_{\rm{a}}}\left( c \right) + {U_{\rm{r}}}\left( c \right) $$ (5) $$ F = {F_{\rm{a}}}\left( c \right) + {F_{\rm{r}}}\left( c \right) $$ (6) 传统PRM算法的构造阶段采用均匀采样，大量节点会落在不可通行区域（待采煤田内部），而在构建概率地图时这些节点需要被舍弃，导致节点不足，无法找到有效的路径，需要重新采样，大大降低了路径规划效率。因此，本文在均匀采样的基础上融合人工势场法，将落在不可通行空间的节点移至可通行空间内，使所有的节点均分布在自由空间内，以提高算法效率。
在PRM算法的构造阶段引入人工势场法，最常用的方法是以每个障碍物为中心建立势能场，但在煤矿井下狭窄通道场景中，该方法存在以下2个问题：① 靠近墙体障碍物内的节点得不到有效的处理，有可能继续留在障碍物中。② 履带式机器人体积较大，若规划的路径与障碍物较为贴近，机器人在狭长自由通道行走时易与障碍物发生碰撞。
因此，本文首先找到距离落在障碍物中的节点最近的自由点，连接此两点形成1条直线，并以指向自由点方向为推出方向，将障碍物中的节点推出；然后设置障碍物边缘斥力为最大；最后在这条直线上寻找斥力最小或斥力为0的点作为新的节点（若障碍物附近不存在其他障碍物或地图边界，则能够找到1个斥力为0的点；若存在其他障碍物，则能够在2个障碍物之间找到1个斥力为0的中间点）。
改进PRM算法构造阶段伪代码如下。
Algorithm PRM算法融合人工势场法构建无向图
repeat
c ← C空间中随机采样1个点；
if碰撞检测后c不在自由空间中
c''' ← 距离c最近的自由空间点； //c'''为距离c最近的节点
$F_{\mathrm{r}} {\text{'}}$ ← c'''受到的斥力；//$F_{\mathrm{r}} {\text{'}}$为节点c'''受到的斥力
repeat
c'' ← c'''；
Fr(c) ←$F_{\mathrm{r}} {\text{'}}$；
c''' ← c''沿c指向c''的方向前进一段步长的新节点；
$F_{\mathrm{r}} {\text{'}}$ ← c'''受到的斥力；
until Fr(c) = 0 或$F_{\mathrm{r}} {\text{'}}$ ＞ Fr(c)或c'''不在自由空间内
c ←c''；
end
将c加入图节点集合，即V ← V∪{c}；
N ← V中c的临近节点集；
for each c' in N
if局部规划器能连接c和c'
将无向边（c，c'）加入图的边集合；
else
将c加入1个新的子图；
end
end
until满足终止条件
2.2 基于D* Lite算法的路径搜索
D* Lite算法以广度优先搜索为基础，采用从目标节点至起始节点的反向扩展方式，利用启发值来提高搜索效率，以实现变起始节点、定目标节点的路径规划，使机器人在突遇障碍物时可实现快速动态重规划，以减少重规划的计算量[19-20]。
路径规划方法的衡量指标除了路径长度外，还需考虑安全性，特别是在未知障碍物的情况下，需要及时重新规划路径。传统PRM算法采用A*算法实现路径搜索，效率较低，实时性差。D* Lite算法具有增量式搜索特性[21]，该算法中任意节点$c $都需维护3个代价g(c)、h(c)和r(c)，其中g(c)为目标节点到当前节点实际代价，h(c)为当前节点到起始节点估计代价，r(c)为当前节点到其所有后继节点的最小代价。
$$ h\left(c\right)=\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{a}\mathrm{b}\mathrm{s}\left({x}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}-{x}_{c}\right),\mathrm{a}\mathrm{b}\mathrm{s}\left({y}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}-{y}_{c}\right)\right) $$ (7) $$ r\left(c\right)=\left\{\begin{array}{l}0\qquad c={c}_{{{\rm{g}}}}\\ \min\limits _{{{c}{{'}}\in {c}_{{{\rm{s}}}}}\left(c\right)}\left(g\left({c}{{'}}\right)+d\left({c}{{'}},c\right)\right)\quad {其}{他}\\ \end{array}\right. $$ (8) 式中：xstart，ystart分别为起始节点的横纵坐标；xc，yc分别为当前节点c的横纵坐标；cs(c)为节点c后继节点；$ d\left({c}{{'}},c\right) $为节点$c' $和节点c之间的移动代价。
通过对每个节点g(c)和r(c)的比较，将节点分为局部欠一致、局部一致和局部过一致3种状态，以保证搜索到的路径更具有启发性[22-23]。算法采用优先队列对需要重新扩展的节点进行保存，以k(c)作为估价函数。
$$ k\left(c\right)=\left({k}_{1}\left(c\right),{k}_{2}\left(c\right)\right) $$ (9) $$ {k}_{1}\left(c\right)={\rm{min}}\left(g\left(c\right),r\left(c\right)\right)+h\left(c\right)+{k}_{{\rm{m}}} $$ (10) $$ {k}_{2}\left(c\right)={\rm{min}}\left(g\left(c\right),r\left(c\right)\right) $$ (11) 式中：k1(c)为节点c的总代价；k2(c)为不包含启发值的代价；km为k1(c)中实际行驶路程的累计代价，可使k1(c)无需进行更新，以提高路径重规划效率。
算法从目标节点cg开始搜索，初始化所有节点，维护优先级列表，取k(c)值最小的节点进行扩展，直到还未扩展的节点中出现k(c)值小于起始节点的k(c)值或起始节点为局部一致节点。从起始节点出发，以满足$\min\limits_{{{c}{{'}}{\in}{c}_{\mathrm{s}}\left(c\right)}}\left(g\left({c}{{'}}\right)+d\left({c}{{'}},c\right)\right)$的节点$c' $作为当前节点c的下一个前进节点，完成路径规划。环境发生变化时，更新变化后的节点，更新km和cs，重新扩展，对改变节点的代价进行更新，进行路径重规划。
因此，本文在PRM算法查询阶段采用D* Lite算法，不仅可有效提高路径搜索效率，还保证了规划路径的安全性。
3. 实验验证
为验证基于改进PRM算法的煤矿机器人路径规划方法的有效性，在Matlab搭建实验场景，如图1所示（x，y为地图的横纵坐标）。场景大小为200 m×200 m，可通行空间为在待开采煤田（黑色区域）中掘出的巷道（白色区域，狭长自由通道），其宽度为6 m。
3.1 融合人工势场法的节点分布评价
设置采样100个节点，对传统PRM算法和改进PRM算法的节点分布情况进行仿真，结果如图2所示。可看出改进PRM算法由于在均匀采样的基础上融合了人工势场法，使得节点分布均匀，且距离未开采区域均有一定距离，提高了路径规划的安全性。
3.2 融合人工势场法的概率地图构建评价
传统PRM算法和改进PRM算法的查询阶段均采用传统A*算法进行路径搜索。设定起始节点为（0，198），终点为（198，0），节点间连接限制步长为30，仿真得到节点数分别为100，200个时规划的全局路径，如图3和图4所示。
由图3和图4可知：当节点为100个时，传统PRM算法路径规划失败，而改进PRM算法成功规划出1条路径；当节点为200个时，传统PRM算法虽然可以规划出路径，但是存在多处转折点且路径贴近障碍物，而改进PRM算法规划的路径转弯次数较少且与障碍物保持一定的安全距离，可有效避免机器人行走时与障碍物碰撞。
为进一步验证改进PRM算法的有效性，分别对节点为100，200，300，400个的情况进行了100次仿真，结果取平均值，统计了路径长度、成功次数、转折点数、运行时间和路径数量等指标，见表1。
表 1 不同节点数量时改进前后PRM算法路径规划结果统计Table 1. Path planning results statistics of probabilistic road map algorithm before and after improvement with different number of sampling nodes算法 节点
数/个成功
次数运行
时间/s路径
长度/m转折点
数/个路径数
量/条传统PRM算法 100 10 3.14 420.35 10 4 200 30 9.78 390.39 8 3 300 61 14.09 381.09 7 2 400 100 29.92 372.78 6 1 改进PRM算法 100 35 2.63 400.93 6 3 200 66 5.13 382.64 5 2 300 97 9.87 372.46 4 1 400 100 19.41 369.57 4 1 由表1可知：当节点为100个时，改进PRM算法路径规划成功率较传统PRM算法提高了25%，且在路径转折点数量、路径长度和路径数量方面都有明显的优势；随着节点数增加，传统PRM算法和改进PRM算法路径规划成功次数均呈增长趋势，但改进PRM算法在效率方面优势更明显；当节点达400个时，传统PRM算法和改进PRM算法路径规划成功率相同，但改进PRM算法在运行效率上提高了35.13%，规划的路径转折点更少，路径更加平滑，且路径长度更短。
3.3 基于D* Lite算法的路径搜索评价
基于人工势场法完成概率地图构建后，在查询阶段采用D* Lite算法进行路径搜索。设定起始节点为（0，198），终点为（198，0），节点间连接限制步长为30，仿真过程中模拟无障碍物、可通行障碍物和不可通行障碍物的情况，以验证改进PRM算法的路径重规划性能。节点为200个时路径规划仿真结果如图5所示。
由图5（a）可知，规划的路径与未开采区域有一定安全距离，表明改进PRM算法能够有效提高路径规划的安全性。由图5（b）可知，当路径上出现障碍物时，若该障碍物不影响道路通行性，改进PRM算法能够将障碍物所在节点的前一节点作为新的起始节点，对路径进行重规划并安全避开障碍物。由图5（c）可知，若该障碍物造成了道路不可通行，改进PRM算法从障碍物所在节点的前一节点到目标节点间重规划出1条新的全局路径。
4. 结论
1） 对PRM算法进行了改进：在构造阶段融合人工势场法，将落在障碍物中的节点沿与其距离最近自由空间中的节点连线方向推至自由空间；在查询阶段采用D* Lite算法代替A*算法，以提高路径搜索效率，保证规划路径的安全性。
2） 仿真结果表明：改进PRM算法的节点分布均匀，且距离障碍物均有一定距离，提高了路径规划的安全性；节点为100个时，改进PRM算法路径规划成功率较传统PRM算法提高了25%；随着节点数增加，传统PRM算法和改进PRM算法路径规划成功次数均呈增长趋势，但改进PRM算法在效率方面优势更明显；当节点为400个时，改进PRM算法运行效率较传统PRM算法提高了35.13%，且规划的路径更加平滑，路径长度更短；当障碍物突然出现时，改进PRM算法能够实现路径的重规划。
-
![]()
图 4 1号测试钻孔各测点应变增量随工作面推进距离变化曲线
Figure 4. Strain increment curves of measuring points in No.1 test borehole during working face advance
![]()
图 5 工作面推进不同距离时底板下垂深10 m处2号测试钻孔孔壁图像
Figure 5. Images of No.2 test borehole wall at 10 m vertical depth of floor with different working face advance distances
![]()
图 6 工作面顶底板工程地质模型纵剖面
Figure 6. Profile of engineering geological model for working face roof and floor
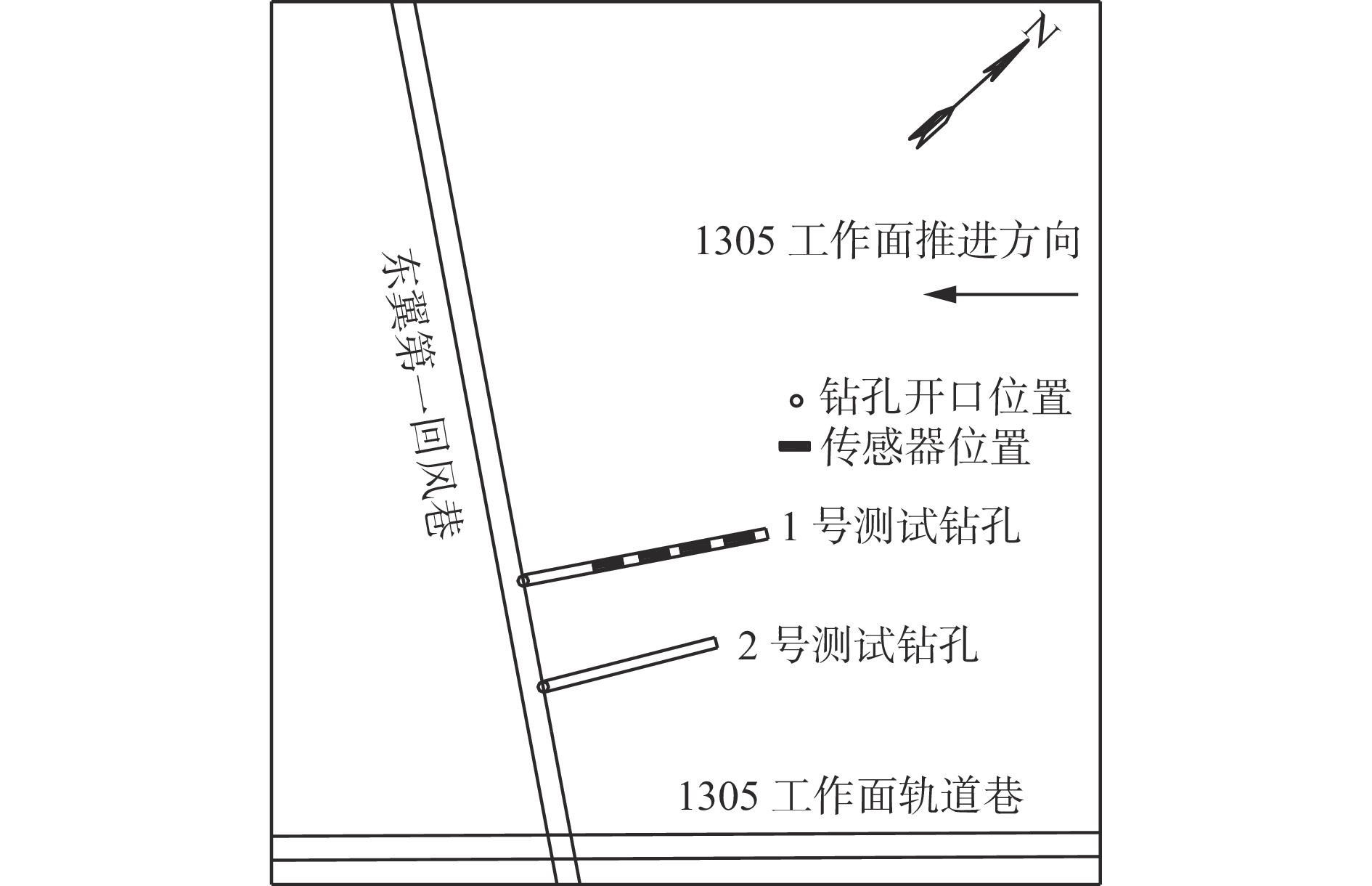
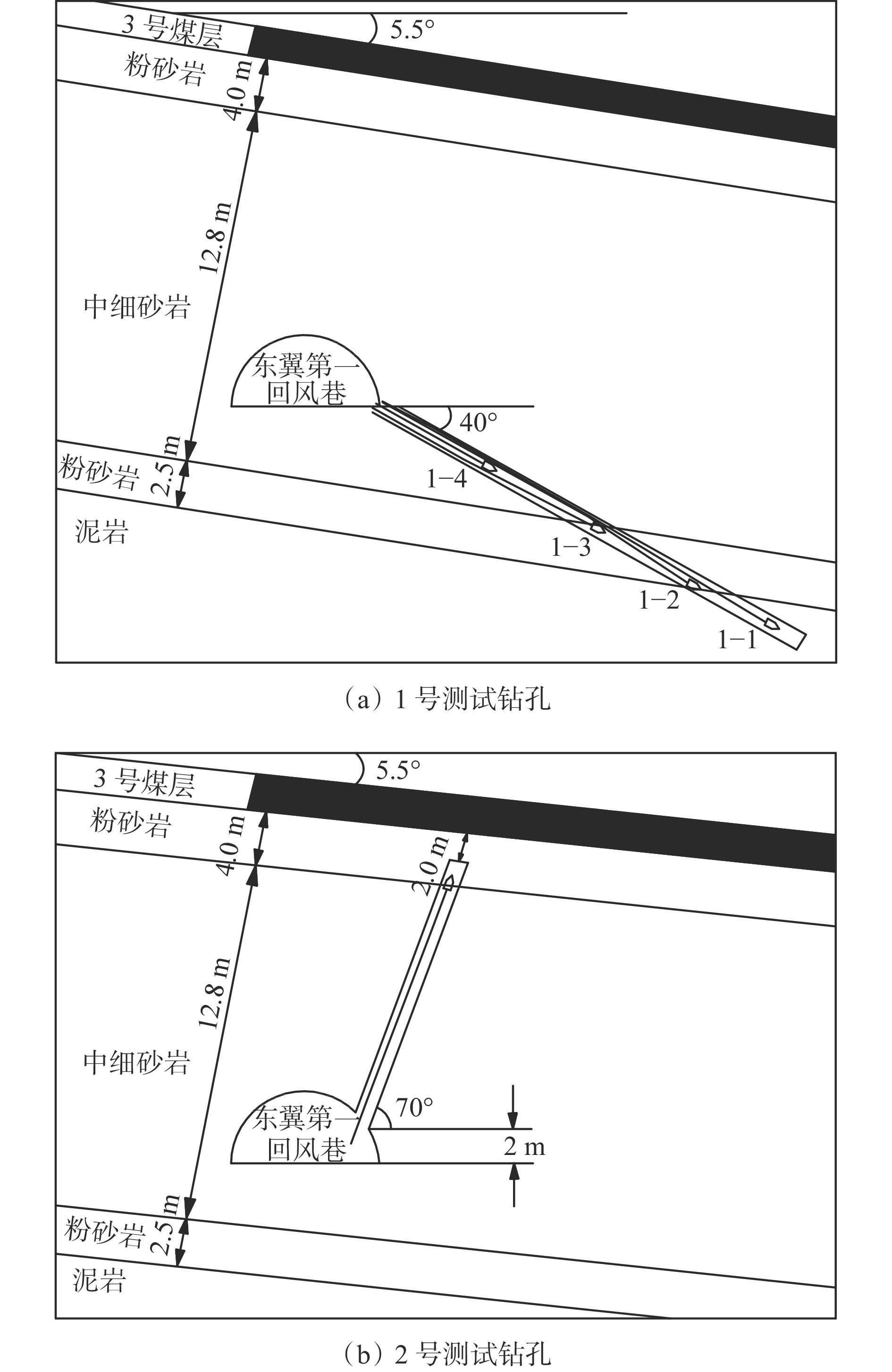
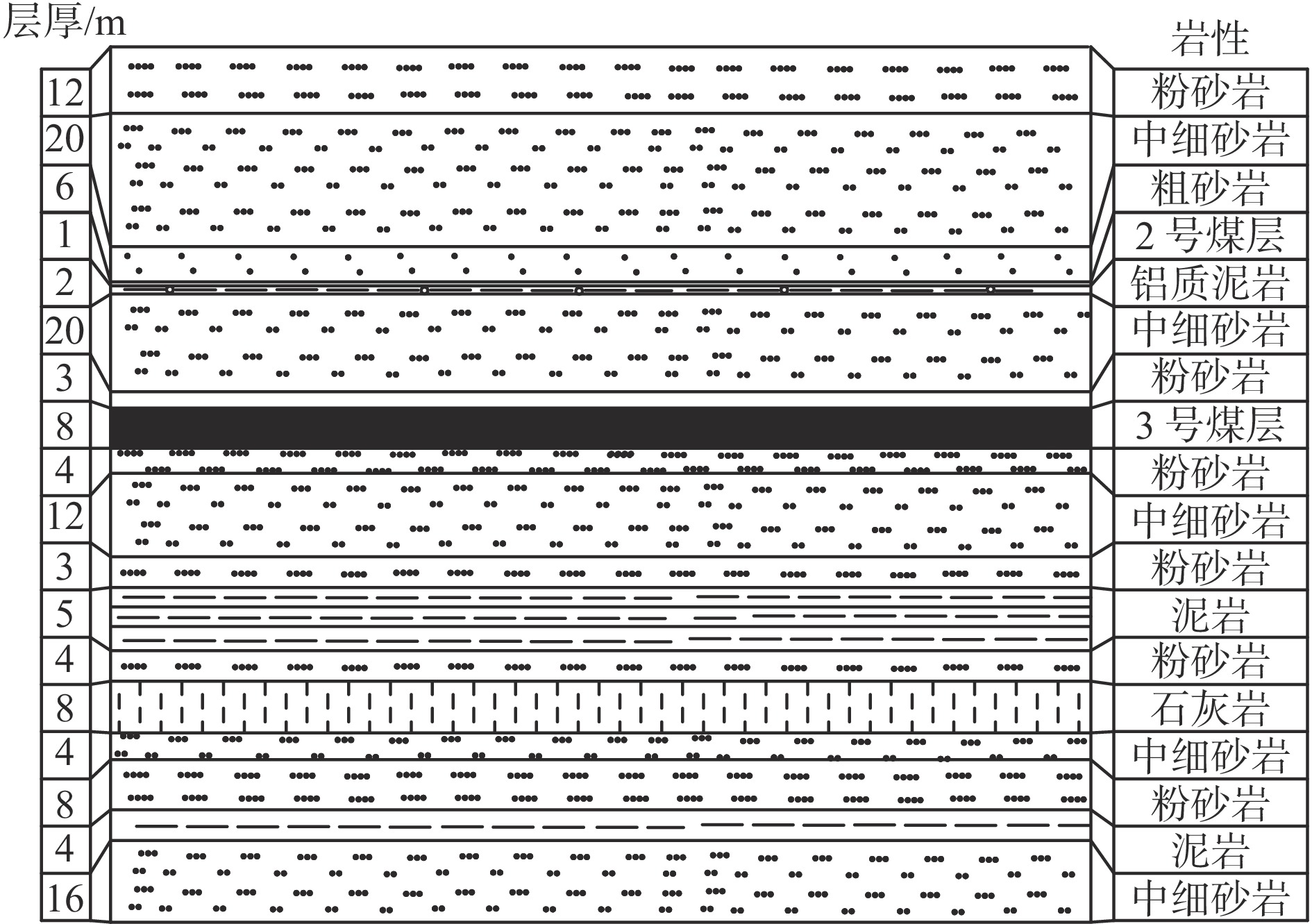
表 1 测试钻孔主要参数
Table 1 Main parameters of test boreholes
参数 1号测试钻孔 2号测试钻孔 开孔直径/mm 127 91 开孔深度/m 2.0 — 孔口管直径/mm 110 — 孔口管长度/m 2.0 — 终孔直径/mm 91 91 钻孔方位角/（°） 31 42 钻孔倾角/（°） 40（俯角） 70（仰角） 钻孔与巷道夹角/（°） 90 80 煤岩层真倾角/（°） 5.6 6.0 钻孔与煤岩层走向线夹角/（°） 81 87 煤岩层视倾角/（°） 5.5 6.0 钻孔总深度/m 30 10 控制3号煤层底板最大真厚度/m 29 11 
下载: 导出CSV
表 2 工作面采动底板变形感应距
Table 2 Deformation induction distances of mining floor of working face
测点垂深/m 超前距/m 滞后距/m 感应范围/m 16 115 — — 20 110 49 159 24 102 48 150 29 96 52 148
下载: 导出CSV
表 3 工作面顶底板岩层物理力学参数
Table 3 Physical and mechanical parameters of working face roof and floor strata
岩层 密度/
（kg·m−3）体积模量/
GPa剪切模量/
GPa黏聚力/
MPa内摩擦角/
（°）抗拉强度/
MPa中细砂岩 2 650 2.90 1.74 9.5 41 4.2 泥质岩 2 550 2.61 1.35 7.6 30 3.0 粗砂岩 2 690 3.35 2.30 10.7 45 4.9 3号煤层 1 400 2.08 0.54 1.2 20 0.6 粉砂岩 2 600 2.91 1.50 7.8 32 3.6 石灰岩 2 800 5.57 4.53 11.4 48 6.7
下载: 导出CSV
-
[1] 国家煤矿安全监察局. 煤矿防治水细则[M]. 北京: 煤炭工业出版社, 2018. State Administration of Coal Mine Safety. Rules for water prevention and control in coal mines[M]. Beijing: China Coal Industry Publishing House, 2018.
[2] 尹尚先,连会青,徐斌,等. 深部带压开采:传承与创新[J]. 煤田地质与勘探,2021,49(1):170-181. DOI: 10.3969/j.issn.1001-1986.2021.01.018 YIN Shangxian,LIAN Huiqing,XU Bin,et al. Deep mining under safe water pressure of aquifer:inheritance and innovation[J]. Coal Geology & Exploration,2021,49(1):170-181. DOI: 10.3969/j.issn.1001-1986.2021.01.018
[3] 刘杰. 特厚煤层综放工作面围岩运动的微地震监测[J]. 矿业安全与环保,2008,35(1):44-46. DOI: 10.3969/j.issn.1008-4495.2008.01.016 LIU Jie. Microseismic monitoring of surrounding rock movement in fully mechanized caving face of extra thick coal seam[J]. Minging Safety & Environmental Protection,2008,35(1):44-46. DOI: 10.3969/j.issn.1008-4495.2008.01.016
[4] 朱术云,曹丁涛,岳尊彩,等. 特厚煤层综放采动底板变形破坏规律的综合实测[J]. 岩土工程学报,2012,34(10):1931-1938. ZHU Shuyun,CAO Dingtao,YUE Zuncai,et al. Comprehensive measurement of characteristics of deformation and failure of extra-thick coal seam floor induced by fully mechanized top-coal mining[J]. Chinese Journal of Geotechnical Engineering,2012,34(10):1931-1938.
[5] 王一栋,姜振泉,朱术云,等. 特厚煤层采动底板变形破坏的数值模拟与实测对比[J]. 煤矿安全,2012,43(10):35-37. DOI: 10.13347/j.cnki.mkaq.2012.10.015 WANG Yidong,JIANG Zhenquan,ZHU Shuyun,et al. Contrast of numerical simulation and field measurement on deformation and failure in thick seam mining floor[J]. Safety in Coal Mines,2012,43(10):35-37. DOI: 10.13347/j.cnki.mkaq.2012.10.015
[6] 李进军,李怀宾,顾合龙. 厚煤层承压水上开采底板破坏规律数值模拟研究[J]. 煤炭技术,2015,34(2):109-111. LI Jinjun,LI Huaibin,GU Helong. Numerical simulation research on damage of thick coal seam mining above confined water on floor[J]. Coal Technology,2015,34(2):109-111.
[7] 杨本水,黄天缘,宣以琼,等. 特厚煤层综放开采底板破坏及阻隔水性能分析[J]. 安徽建筑大学学报,2019,27(3):28-33. YANG Benshui,HUANG Tianyuan,XUAN Yiqiong,et al. Bottom destruction and barrier performance analysis of fully mechanized caving mining in extra-thick coal seam[J]. Journal of Anhui Jianzhu University,2019,27(3):28-33.
[8] 范红伟,杨涛. 近距离特厚煤层采动影响下底板破坏及巷道稳定性研究[J]. 矿业研究与开发,2021,41(5):107-112. FAN Hongwei,YANG Tao. Research on floor failure and roadway stability under the influence of mining in near-distance extra-thick coal seam[J]. Mining Research and Development,2021,41(5):107-112.
[9] 张郑伟. 特厚煤层综放开采对底板变形损伤的影响研究[J]. 同煤科技,2021(3):7-10. ZHANG Zhengwei. Study on influence of fully mechanized top coal caving mining on deformation and damage of floor in extra thick coal seam[J]. Datong Coal Science & Technology,2021(3):7-10.
[10] 陈洋. 大同矿区特厚煤层采动底板变形及破坏深度研究[D]. 徐州: 中国矿业大学, 2021. CHEN Yang. Study on deformation and failure depth of mining-induced floor of extra-thick coal seam in Datong Mining Area[D]. Xuzhou: China University of Mining and Technology, 2021.
[11] 高银贵,孔皖军,陈永春,等. 特厚煤层综放开采下工作面底板岩层破坏特征[J]. 能源环境保护,2021,35(6):68-75. DOI: 10.3969/j.issn.1006-8759.2021.06.010 GAO Yingui,KONG Wanjun,CHEN Yongchun,et al. Study on the failure characteristics of the bottom slate layer in the working face of fully mechanized caving in ultra-thick coal seam[J]. Energy Environmental Protection,2021,35(6):68-75. DOI: 10.3969/j.issn.1006-8759.2021.06.010
[12] 王升阳,张志巍. 厚煤层综放开采底板采动破坏及渗流特征[J]. 能源与节能,2022(4):10-14. DOI: 10.3969/j.issn.2095-0802.2022.04.003 WANG Shengyang,ZHANG Zhiwei. Mining failure and seepage characteristics of fully mechanized caving floor in thick coal seams[J]. Energy and Energy Conservation,2022(4):10-14. DOI: 10.3969/j.issn.2095-0802.2022.04.003
[13] 郭国强. 综放开采特厚煤层采场底板破坏规律研究[J]. 煤田地质与勘探,2022,50(8):53-61. DOI: 10.12363/issn.1001-1986.21.12.0774 GUO Guoqiang. Floor failure law of extra-thick coal seam in fully mechanized caving mining[J]. Coal Geology & Exploration,2022,50(8):53-61. DOI: 10.12363/issn.1001-1986.21.12.0774
[14] 于小鸽, 施龙青, 韩进, 等. 损伤底板破坏深度预测理论及应用[M]. 北京: 煤炭工业出版社, 2016. YU Xiaoge, SHI Longqing, HAN Jin, et al. Theory and application of failure depth prediction of damaged floor[M]. Beijing: China Coal Industry Publishing House, 2016.
[15] 钱鸣高, 石平五. 矿山压力与岩层控制[M]. 徐州: 中国矿业大学出版社, 2003. QIAN Minggao, SHI Pingwu. Mine pressure and rock control[M]. Xuzhou: China University of Mining and Technology Press, 2003.
-
期刊类型引用(17)
1. 郭辉，刘祚时，黄鹏，宋诗强. 基于改进RRT-Connect算法的机械臂路径规划. 组合机床与自动化加工技术. 2025(03): 41-45+54 . 
百度学术
2. 李莉. 高层建筑突发性火灾逃生路径快速规划方法研究. 建设科技. 2025(03): 90-92 . 百度学术
3. 李益沛，宋鹏波，赵嘉琦，章玉龙. 一种复杂场景下便捷通行路径规划新方法. 粘接. 2025(05): 147-150 . 百度学术
4. 陈云. 基于改进蚁群算法的农田水利灌区水管路径规划方法. 水利技术监督. 2024(01): 69-71+114 . 百度学术
5. 滕卓易. 基于蚁群算法的新能源汽车最优行驶路径规划. 无线互联科技. 2024(09): 12-14 . 百度学术
6. 王丽丽. 基于改进RRT算法的井下巷道漫游路径规划方法. 现代电子技术. 2024(12): 62-68 . 百度学术
7. 薛光辉，王梓杰，王一凡，李亚男，刘文海. 基于改进人工势场算法的煤矿井下机器人路径规划. 工矿自动化. 2024(05): 6-13 . 本站查看
8. 赵思文，朱津欣. 基于改进蚁群算法的电力电缆敷设路径规划方法. 电气技术与经济. 2024(06): 322-323+327 . 百度学术
9. 李鹏程. 融合PRM算法与弹性绳算法的路径规划算法. 电脑编程技巧与维护. 2024(07): 36-39 . 百度学术
10. 周俊霄，唐晓峰. 概率路线图环境下自动驾驶路径规划优化. 自动化应用. 2024(13): 16-19 . 百度学术
11. 黄以成. 融合改进A*和DWA算法的物流机器人自主导航及路径规划研究. 互联网周刊. 2024(15): 23-25 . 百度学术
12. 黄佳德，刘勇，邓穆坤，梅文庆. 露天矿场无人驾驶自卸车路径规划方法研究. 煤炭科学技术. 2024(08): 182-191 . 百度学术
13. 李忠林，罗邵屏，贾玉婷. 移动机器人路径规划算法综述. 现代信息科技. 2024(19): 184-188 . 百度学术
14. 郭小莹，赵淑苹. 机器人路径规划中的算法研究综述. 无线电工程. 2024(11): 2664-2671 . 百度学术
15. 殷宏亮，朱洪波. 融合目标导向和跳跃点改进A*算法的煤矿巡检机器人路径规划. 煤矿机械. 2024(12): 180-184 . 百度学术
16. 韩雷，云龙. 基于FDH包围盒算法的煤矿井下机器人避障最小安全距离控制. 中国煤炭. 2024(S1): 21-27 . 百度学术
17. 刘学宏，马浩东，付可，陈玲玲. 预规划最优快速探索随机树. 电脑与电信. 2023(12): 56-58+82 . 百度学术
其他类型引用(16)
计量
- 文章访问数: 231
- HTML全文浏览量: 64
- PDF下载量: 29
- 被引次数: 33
