0.   引言

随着科技的不断进步，煤矿井下运输作业正逐渐向自动化和智能化转型^[1]。然而，煤矿井下环境的复杂性给运输作业带来了巨大挑战。无人驾驶技术是实现矿用车辆安全高效智能化运输的重要技术手段，也是煤炭行业智能化发展的必然趋势，可使车辆能够在极端环境下代替人的操作自主完成未知环境感知、车辆定位和导航，从而控制车辆运动^[2-3]。煤矿井下全局路径规划是指在煤矿井下复杂环境中为运输机器人或自动化运输设备设计出一条从起点到终点的最优路径^[4-5]。路径规划是无人驾驶技术的核心，深入研究矿用无人驾驶车辆的路径规划问题对提升煤矿井下运输效率具有重大意义^[6-7]。

全局路径规划侧重于在已知环境地图的基础上计算一条从起点到终点的最优路径，通常涉及到图搜索算法，如A^*算法、Dijkstra算法等^[8]，这些算法能够在地图上搜索出一条避开所有已知障碍物的路径。崔宝侠等^[9]对传统的A^*算法进行了改进，将8邻域搜索扩展为24邻域搜索，减少了规划路径的长度，但增加了计算时间。程传奇等^[10]对A^*算法的启发式搜索函数进行了优化，在保留路径规划过程中关键节点的同时，去除了冗余节点和不必要的转折点，从而提高了路径规划的效率和准确性。C. Richter等^[11]提出了一种基于学习启发式函数的路径搜索方法，提高了对未知空间的可见性，但这种方法在复杂三维环境中的适用性有限。H. Oleynikova等^[12]结合全局规划和局部探索方法，实现了复杂环境中的安全行驶，但在已知空间范围内选择中间目标时较为保守，导致执行时间较长。黄迎港等^[13]针对复杂环境设计了复合策略，以应对随机事件问题，增强了环境感知能力。针对井下巷道环境中的路径规划，袁晓明等^[14] 提出了一种集成先进感知、精确定位和智能路径规划的煤矿辅助运输机器人技术方案，但该方案可能面临成本高、计算复杂、环境适应性及传感器性能受限等挑战。黄友锐等^[15]提出了结合膜计算和Informed RRT的路径规划方法，通过调整步长和并行计算优化狭窄空间的路径搜索，提高了搜索效率和路径平滑性，但存在参数敏感性和泛化能力有限的问题。薛光辉等^[16]提出了一种改进的人工势场算法，用于解决煤矿井下机器人在狭窄巷道中的目标不可达和路径振荡问题，通过建立巷道边界势场、引入斥力势场调节因子和转角限制系数，提高了路径规划的安全性和效率。夏静慧等^[17] 提出了一种改进人工势场算法，通过优化引力和斥力势场模型并引入道路边界斥力势场，有效解决了传统算法中的局部最小值和路径偏离问题，提高了矿车在复杂矿区环境中的避障和行进效率，但参数选择可能需要进行大量实验。

为了提高矿用车辆在狭窄、弯曲及有未知障碍物的井下巷道中的路径规划效率，将环境地图的建立和路径搜索的过程融合在一起，提出了一种融合简化可视图（Simplified Visibility Graph，SVG）和A^*算法的全局路径规划算法DVGA^*。通过动态生成环境地图并简化，得到可视图；将车辆在不同视点下选取的可视切点依次存入${\mathrm{OPEN}}$表，结合A^*算法的估价函数在${\mathrm{OPEN}}$表中选取最短路径节点放入${\mathrm{CLOSED}}$表并存储路径，同时删除${\mathrm{CLOSED}}$表中的其余节点，从而对链表进行动态更新，循环此过程，直到${\mathrm{OPEN}}$表中出现终点；使用路径平滑算法对链表中的路径节点进行优化，得到最优路径。

1.   SVG原理

全局路径规划可看成一个四元函数问题：

式中：$P$为路径节点序列；$f$（·）为路径规划函数；$S$为起始位置；$G$为目标位置；$Z$为障碍物集合；$Q$为搜索空间。

在搜索空间$Q$中，以起始位置$S$为起点、目标位置$G$为终点开始搜索。如果存在路径节点序列$P$=$\{ {P_1},{P_2},\cdots ,{P_n}\} $（n为节点总数），使得${P_1} = S$,${P_n} = G$，且路径节点序列中没有任何点与障碍物集合$Z$相交，那么该路径节点序列就是全局路径规划问题的一组解。

可视图是一种图结构，其节点代表障碍物顶点，边表示节点之间可视连通性^[18-19]。如果2个节点之间的连线没有被任何障碍物阻挡，则在这2个节点之间添加一条边。这种方法将环境转换为一个图结构，其中节点集合包括起点、目标点和障碍物顶点，边集合则是这些点之间的可视直线段。构建可视图时，将起点与视野内所有障碍物轮廓点相连并判断连线是否穿过障碍物，若穿过则为无用路径节点，若不穿过则计算其余轮廓点与终点的距离，选择距离最短的轮廓点进行视野更新，并删除之前的障碍物轮廓点和连线，达到简化路径节点和可视边的效果。

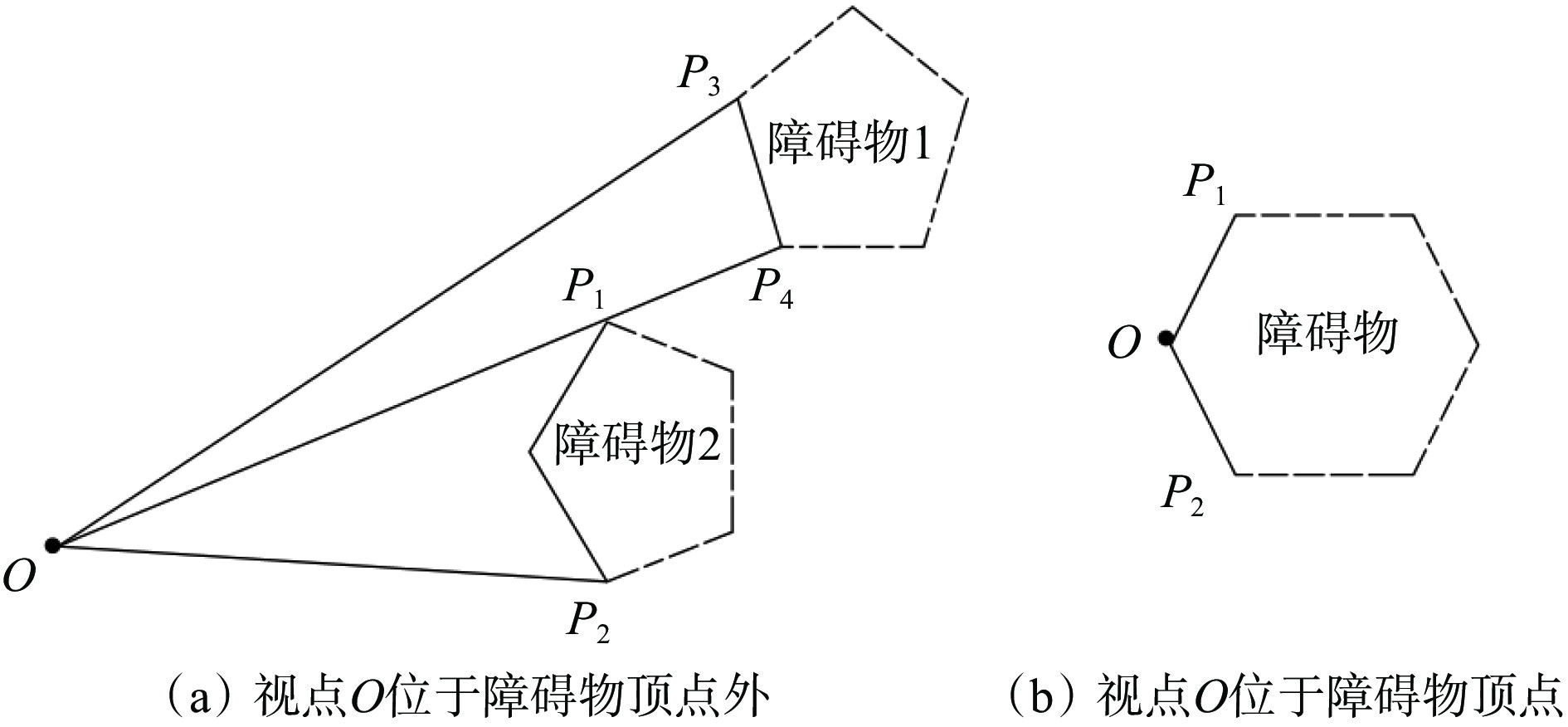
以矿用车辆为例，将观测位置称为视点，在车辆视野范围内的障碍物称为可视障碍物。当视点$ O $位于障碍物顶点外（图1（a））时，连接视点$ O $与可视障碍物的边界并作延长线，若延长线不与障碍物其他部分相交，则该延长线称为可视切线，可视障碍物的边界点即为可视切点，即$ {P_1},{P_2} $是可视切点，$ {P_3},{P_4} $不是可视切点。当视点$ O $位于障碍物顶点（图1（b））时，与视点O相邻的顶点${P_1}$和${P_2}$为可视切点，与视点$O$相连的边$O{P_1}$和$O{P_2}$称为可视切线。判断车辆视野范围内所有障碍物顶点中哪些点为可视切点，若不是可视切点则为无用路径点，使用A^*算法估价函数时只考虑可视切点，从而达到简化目的。

图  1  可视切线及可视切点

Figure  1.  Visual tangents and visual tangent points

下载: 全尺寸图片 幻灯片

动态切线可视图通过可视切线表示车辆的可行路径。在动态环境中，当障碍物的位置或形状发生变化时，动态切线可视图能够快速更新，以反映新的可见性关系。随着车辆的移动，通过传感器不断更新可见区域，并根据新的环境信息利用某种搜索算法调整路径。最终，车辆通过不断探索和更新路径，逐步接近目标点并找到一条安全路径。动态切线可视化如图2所示，黑色多边形表示障碍物。

图  2  动态切线可视化

Figure  2.  Dynamic tangents visualization

下载: 全尺寸图片 幻灯片

2.   融合SVG和A^*算法的DVGA^*算法

2.1   A^*算法

全局路径规划算法主要分为启发式搜索和智能算法。A^*算法^[8]是一种用于图搜索和路径查找的启发式搜索算法，结合了Dijkstra算法的优点和启发式搜索的灵活性，通过对路径进行估价，找到从起点到目标点的最短路径。A^*算法基于启发函数构造了估价函数，既考虑了新节点到起点的代价，又考虑了新节点到目标点的代价。

式中：$F(n)$为起点经过当前节点到目标点的估价函数；$g(n)$为当前节点到目标点的实际代价；$h(n)$为启发函数，是从当前节点到达目标点最佳路径的估计代价。

2.2   路径生成

DVGA^*算法原理如图3所示，其中实线表示障碍物的边可见，虚线表示障碍物的边不可见。对于矿用车辆来说，其路径是由可视切线构成的，没有先验地图的情况下，车辆只能依靠传感器获得当前环境信息。随着车辆视点位置变化，障碍物的可见性也在发生变化。车辆视点在不同位置可看到的障碍物边界也在不断发生变化。当车辆的视点位于$O$点时，在可视范围内，传感器只能检测到彼此互不遮挡的障碍物1和障碍物2，因此可视切线图包含４条可视切线和４个可视切点。为了走出当前障碍区且不与障碍物相碰，车辆根据A^*算法进行计算，最终选择可视切线图中的可视切点${O_1}$作为子目标点。车辆将可视切点${O_1}$作为新的视点，在以${O_1}$为视点的新视窗内，车辆视点范围内可视切线图包含6条可视切线和6个可视切点，如图3（b）所示。同理，按照A^*算法策略，选取其中一条路径，依此类推，直至到达目标点。

图  3  DVGA^*算法原理

Figure  3.  Principle of DVGA^* algorithm

下载: 全尺寸图片 幻灯片

DVGA^*算法的估价函数为$F'({O_i}) = g'({O_i}) + h'({O_i})$，与A^*算法估价函数选取一致，$g'({O_i})$为从起点${O_{{\mathrm{start}}}}$到节点${O_i}$的路径长度；$h'({O_i})$为启发函数，即从节点${O_i}$到终点${O_{{\mathrm{goal}}}}$的直线距离。节点${O_i}$与${O_{{\mathrm{goal}}}}$的距离越近，$F'({O_i})$越小，矿用车辆的搜索范围越靠近目标。

在搜索过程中需设置2张表：${\mathrm{OPEN}}$表和${\mathrm{CLOSED}}$表。${\mathrm{OPEN}}$表保存后续待扩展节点，${\mathrm{CLOSED}}$表用于保存从起点开始获取的路径节点。

根据几何路径点构造双向链表。${\mathrm{OPEN}}$表的表达式为$ {\mathrm{OPEN}}(i)=\{{\mathrm{Number}},g'({O}_{i}),h'({O}_{i}), {\mathrm{prev}},{\mathrm{Count}}\} $，其中${\mathrm{Number}}$为可视切点在可视切线图中的编号；${\mathrm{prev}}$为上一节点的索引号，${\mathrm{prev}}$为0表示该节点是起点；${\mathrm{Count}}$为节点访问次数，用来避免重复访问相同节点。${\mathrm{CLOSED}}$表的表达式为${\mathrm{CLOSED}}(i) = \{ {\mathrm{Number}}, {\mathrm{prev}}\} $。

DVGA^*算法的具体步骤如下：

1） 创建空链表${\mathrm{OPEN}}$和${\mathrm{CLOSED}}$，将起点${O_{{\mathrm{start}}}}$放入${\mathrm{CLOSED}}$表中。

2） 通过车辆视点确定起点到车辆视点范围内障碍物1和障碍物2的可视切点{A₁和A₂，B₁和B₂}，将确定的可视切点插入待扩展列表${\mathrm{OPEN}}$中，若车辆想要越过障碍物1和障碍物2，必然要通过${\mathrm{OPEN}}$表中现存的任一可视切点。

3） 根据DVGA^*算法的估价函数计算${\mathrm{OPEN}}$表中待扩展可视节点的评价值，选择$F'({O_i})$值最小的节点（即估计路径最短的可视切点）来扩展。

4） 将选出的扩展可视切点A₂添加到${\mathrm{CLOSED}}$表中作为最优路径点，并将其边存储为路径。

5） 清空${\mathrm{OPEN}}$表中除A₂外的其他节点，将A₂作为车辆的下一个视点，重复步骤2）−步骤4）。

6） 若车辆视点范围内出现了终点${O_{{\mathrm{goal}}}}$，直接将其插入${\mathrm{CLOSED}}$表中，路径搜索结束。

DVGA^*算法路径搜索伪代码如下。

DVGA^*算法与A^*算法的主要区别：A^*算法的${\mathrm{OPEN}}$表保留了之前步骤的所有已扩展节点，而DVGA^*算法的${\mathrm{OPEN}}$表只保存当前扩展节点的后续待扩展节点，删除了之前步骤中的已扩展节点，大大减少了${\mathrm{OPEN}}$表中保存的节点数量，从而降低了计算量和耗时。

2.3   路径平滑

${\mathrm{CLOSED}}$表中保存的是一条从起点到终点的路径，受启发函数的限制，获取的路径不保证为最短路径。为了有效移除路径中的冗余节点，使用路径平滑算法消除冗余节点。路径平滑流程如图4所示。

图  4  路径平滑流程

Figure  4.  Path smoothing process

下载: 全尺寸图片 幻灯片

对于路径上的每个节点，检查是否可直线到达下一个节点。如果${\mathrm{CLOSED}}$表中第 i+1 号节点为终点则算法结束，否则通过SMOOTH算法^[20]判断第i号节点到第i+2号节点之间是否存在直线可达性，即2个点之间能否连成不穿过障碍物的直线，如果存在则认为这2个节点可直接相连，第 i+1 号节点是可从路径中删除的冗余节点。如果第 i 号节点与第 i+2 号节点不存在直线可达性，则将 i 增加1，检查下一个节点。不断重复这个过程，直到路径中的第 i+1 号节点为终点，算法结束。最终输出的路径即为平滑后的路径，删除了所有不必要的中间节点，从而更直接和简洁。路径平滑前后对比如图5所示。

图  5  路径平滑前后对比

Figure  5.  Comparison of path before and after smoothing

下载: 全尺寸图片 幻灯片

3.   全局路径规划仿真实验及井下试验

3.1   全局路径规划仿真

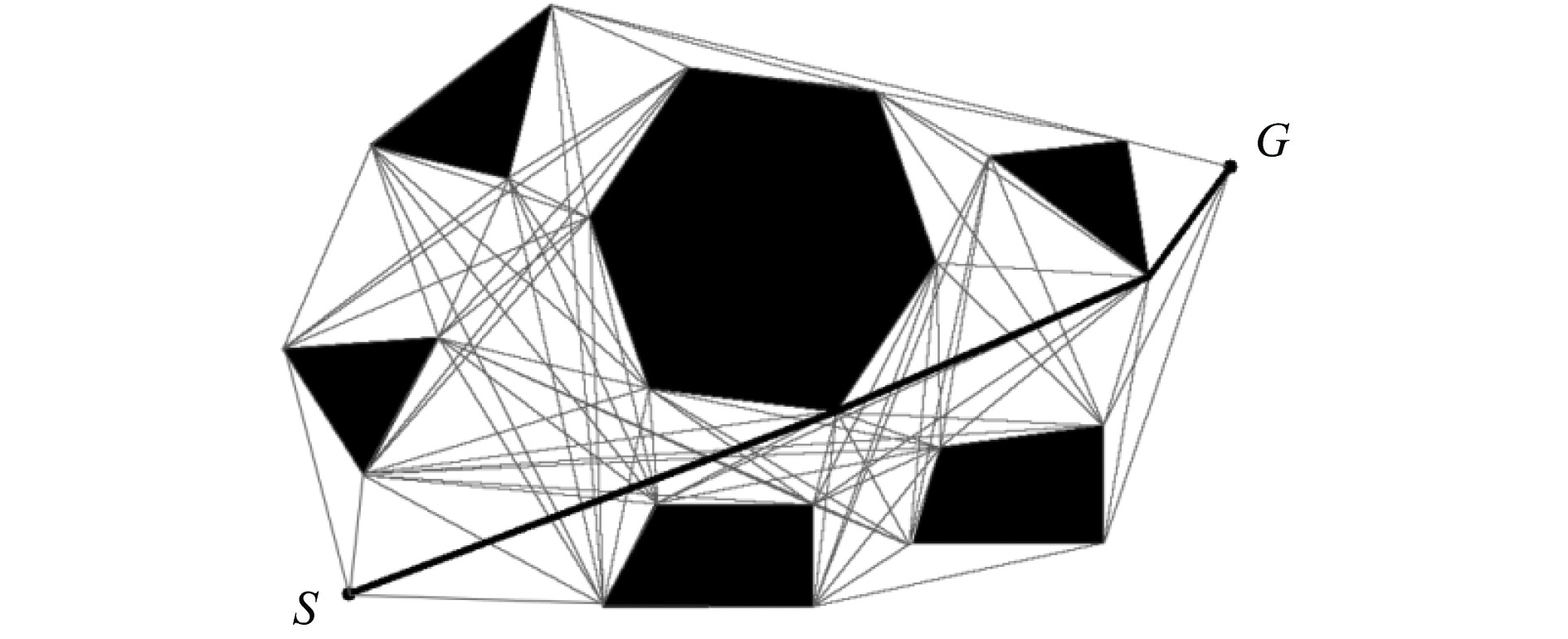
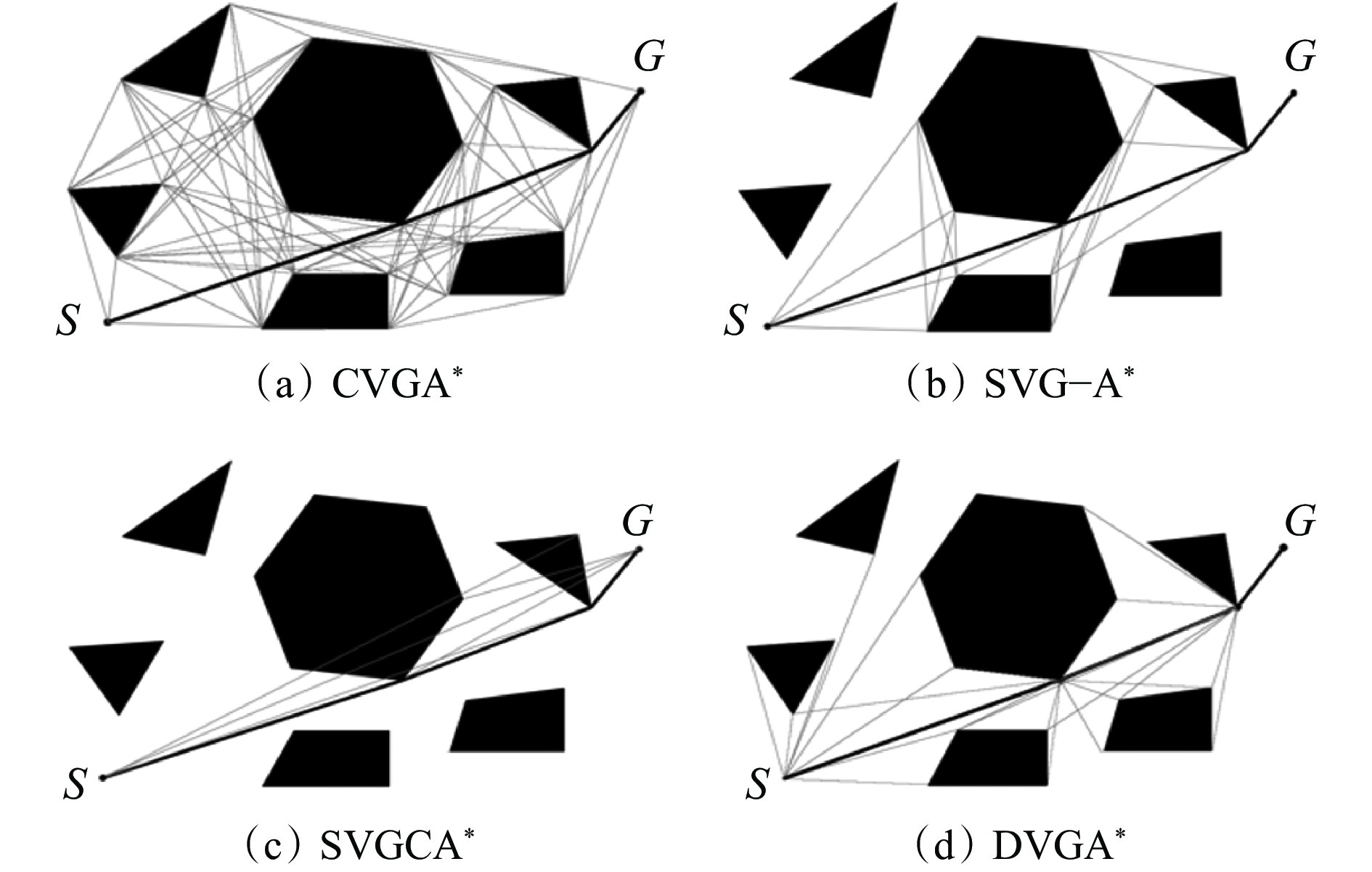
为了验证DVGA^*算法的有效性，设置模拟环境地图，其中包含6个随机生成的障碍物，障碍物占环境地图总面积的40%，起点和终点分别为S和G。应用4种算法在二维环境中进行路径规划仿真实验，结果如图6所示。第1种算法为完整可视图+A^*算法（CVGA^*），建立完整可视图后，使用A^*算法搜索最优路径，可看出该算法在前期可视地图的构建上消耗了大量时间，而其中大部分可视边与搜索出的最终路径无关，可视边数量的增加导致A^*算法搜索效率低下。第2种算法为DVG+A^*算法（SVG−A^*），使用文献[21]中的方法建立SVG后，再使用A^*算法搜索最优路径，由于障碍物影响搜索路径，所以SVG−A^*算法的效率不高。第3种算法为SVGCA^*算法^[8]，利用穿越线筛选可视点并同步生成可视图，该算法需要在可视点之间构建穿越线来确定是否存在障碍物并确定可视点，虽然扩展的节点数有所减少，但是算法迭代次数较多。第4种算法为DVGA^*算法，通过车辆视点直接确定障碍物的可视切点，相比SVG−A^*算法减少了${\mathrm{OPEN}}$表中的节点数量，动态生成可视图并通过平滑算法使路径搜索更加高效。

图  6  模拟环境下4种算法规划路径对比

Figure  6.  Comparison of path planning by four algorithms in a simulated environment

下载: 全尺寸图片 幻灯片

模拟环境下4种算法的路径规划数据见表1。CVGA^*算法过于繁琐且耗时长，SVG−A^*算法可视图构建和路径查找加快，但仍不满足实时应用要求。SVGCA^*算法缩短了可视图的构建时间和$ {\mathrm{OPEN}} $表长度，算法执行时间仅为SVG−A^*算法的20%。DVGA^*算法的扩展节点数量和$ {\mathrm{OPEN}} $表长度远小于其他3种算法，因此路径搜索时间显著缩短。DVGA^*算法构建的可视图耗时不到SVG−A^*算法的20%，$ {\mathrm{OPEN}} $表长度最短。无论是时间复杂度，还是空间复杂度，DVGA^*算法都优于其他3种算法。

表  1  模拟环境下4种算法的路径规划数据

Table  1.  Path planning data for four algorithms in a simulated environments

算法	可视 边数	算法执 行时间/s	可视图 构建时间/s	路径查 找时间/s	路径 长度/m	${\mathrm{OPEN}}$ 表长度
CVGA*	108	0.78	0.70	0.08	769.85	73
SVG−A*	40	0.53	0.50	0.03	769.85	20
SVGCA*	2	0.11			769.85	4
DVGA*	32	0.10	0.09	0.01	769.85	3

下载: 导出CSV 

| 显示表格

3.2   全局路径规划实验

为了进一步验证DVGA^*算法在实际应用中的可靠性和有效性，选取智能小车为实验对象开展全局路径规划实验。智能小车如图7所示，底盘系统由前置阿克曼式转向机构、后置独立双电动机及驱动器组成，为小车提供驱动力。工控机搭载ROS操作系统，同时嵌入路径规划算法，通过CAN总线与车辆底盘进行交互通信，将运行指令发送到控制底盘，驱动器下发指令驱动小车电动机旋转，进而实现小车的定位和路径规划。实验硬件设备信息见表2。

图  7  智能小车

Figure  7.  Intelligent car

下载: 全尺寸图片 幻灯片

表  2  实验硬件设备信息

Table  2.  Experimental hardware equipment information

设备名称	型号
上位机	CPU i7−9700，RTX 3060，ROS Melodic
激光雷达	velodyne VLP−16
惯性测量单元	LPMS−IG1
相机	D435i

下载: 导出CSV 

| 显示表格

选择楼道作为实验场地，楼道结构简单、特征点少，与井下巷道环境的整体分布较为相似，并能模拟场景退化问题，如图8所示。

图  8  模拟巷道实验场景

Figure  8.  Simulated roadway experiment scene

下载: 全尺寸图片 幻灯片

在已知全局地图上添加2个未知物体，一个是静态的矩形箱子A，另一个是匀速运动的障碍物B，设置起点和目标点。对CVGA^*，SVG−A^*，SVGCA^*及DVGA^*算法进行对比实验，点云地图构建及路径规划结果如图9所示。图9（a）和图9（b）表明，在躲避静态障碍物A时，CVGA^*和SVG−A^*算法规划的轨迹在巷道转角的转弯半径较大；图9（c）和图9（d）表明，SVGCA^*和DVGA^*算法在巷道转角的转弯路径很平滑，但SVGCA^*算法避障距离较大。在躲避动态障碍物B时，CVGA^* 算法的避障路径弯曲、易发生碰撞且没有到达目标点，SVG−A^*算法的避障距离过大，SVGCA^*算法的避障距离比SVG−A^*算法小，而DVGA^*算法在小范围内躲避障碍物B后很快到达了目标点，整体路径较为平滑。

图  9  点云地图构建及路径规划结果

Figure  9.  Point cloud map construction and path planning results

下载: 全尺寸图片 幻灯片

DVGA^*算法规划路径局部放大如图10所示，可看出静态障碍物A处避障半径较小，在巷道转角和动态障碍物B处路径更加平滑，避障路径更加有效，同时避障前后路径都近似直线，运行更加稳定。

图  10  DVGA^*算法规划路径局部放大

Figure  10.  Local amplification of DVGA^* algorithm planning path

下载: 全尺寸图片 幻灯片

采用4种算法实验时智能小车轨迹对比如图11所示，t为时间，x，y为移动距离，$\omega $为航偏角。由图11（a）可看出，4种算法在x方向的移动距离相近，CVGA^*算法在y方向没能到达预设的目标点且加速度存在多次突变，运行不稳定，其余算法在y方向表现出更好的稳定性。由图11（b）可看出，采用DVGA^*算法时航偏角变化稳定、迅速，小车行驶更加平稳，路径规划更加灵活。

图  11  智能小车实验轨迹对比

Figure  11.  Comparison of experimental trajectories of the intelligent car

下载: 全尺寸图片 幻灯片

分别应用4种算法进行30次路径规划实验，得到平均路径长度、平均规划时间和到达目标点的成功次数，见表3。可看出相较于CVGA^*，SVG−A^*和SVGCA^*算法，DVGA^*算法平均规划时间分别减少了38.18% ，24.69%和16.05% ；平均路径长度分别缩短了10.79 % ，6.26% 和2.86% ；同时，DVGA^*算法成功次数最多。上述结果表明，DVGA^*算法提高了小车在复杂环境下路径规划的成功率，增强了算法对环境的适应能力，路径规划更快。

表  3  不同算法实验数据对比

Table  3.  Comparison of experimental data for different algorithms

算法	平均规划时间/s	平均路径长度/m	成功次数
CVGA*	296	75.107	20
SVG−A*	243	71.454	23
SVGCA*	218	68.981	26
DVGA*	183	67.005	30

下载: 导出CSV 

| 显示表格

3.3   煤矿井下巷道全局路径规划试验

实际的煤矿井下会出现巷道狭窄、弯曲及有未知障碍物的情况，为进一步测试DVGA^*算法在真实复杂环境中的性能，开展煤矿井下巷道全局路径规划试验。井下巷道环境如图12所示。相比长直廊道，该巷道存在直道、拐弯、分叉及2种不同宽度。从起点出发直行20 m，经过一个曲率较小的拐弯后到达宽巷道，巷道右侧存在紧靠墙壁的管道设备，其直径为1 m，长度为2 m，设备前方12 m处存在分叉路口。进入窄巷道并经过曲率较大的拐弯后恢复到直行巷道，巷道顶部每隔10 m有一个照明光源。

图  12  井下巷道环境

Figure  12.  Underground roadway environment

下载: 全尺寸图片 幻灯片

应用SVGCA^*和DVGA^*算法分别进行路径规划试验，规划路径如图13所示。在巷道宽度变换区域和躲避静态障碍物A时，相比SVGCA^*算法，DVGA^*算法规划的路径更加平滑；在经过一个较大的半U型弯道和曲率较大的拐弯时，为躲避动态障碍物B，SVGCA^*算法规划出曲率较大的弯曲路径并经过一段距离后才恢复到近似直线的路径上来，而DVGA^*算法在避开动态障碍物B的同时及时进行路径纠正，保证了路径规划的时效性和稳定性。

图  13  井下巷道路径规划试验结果

Figure  13.  Experimental results of underground roadway path planning

下载: 全尺寸图片 幻灯片

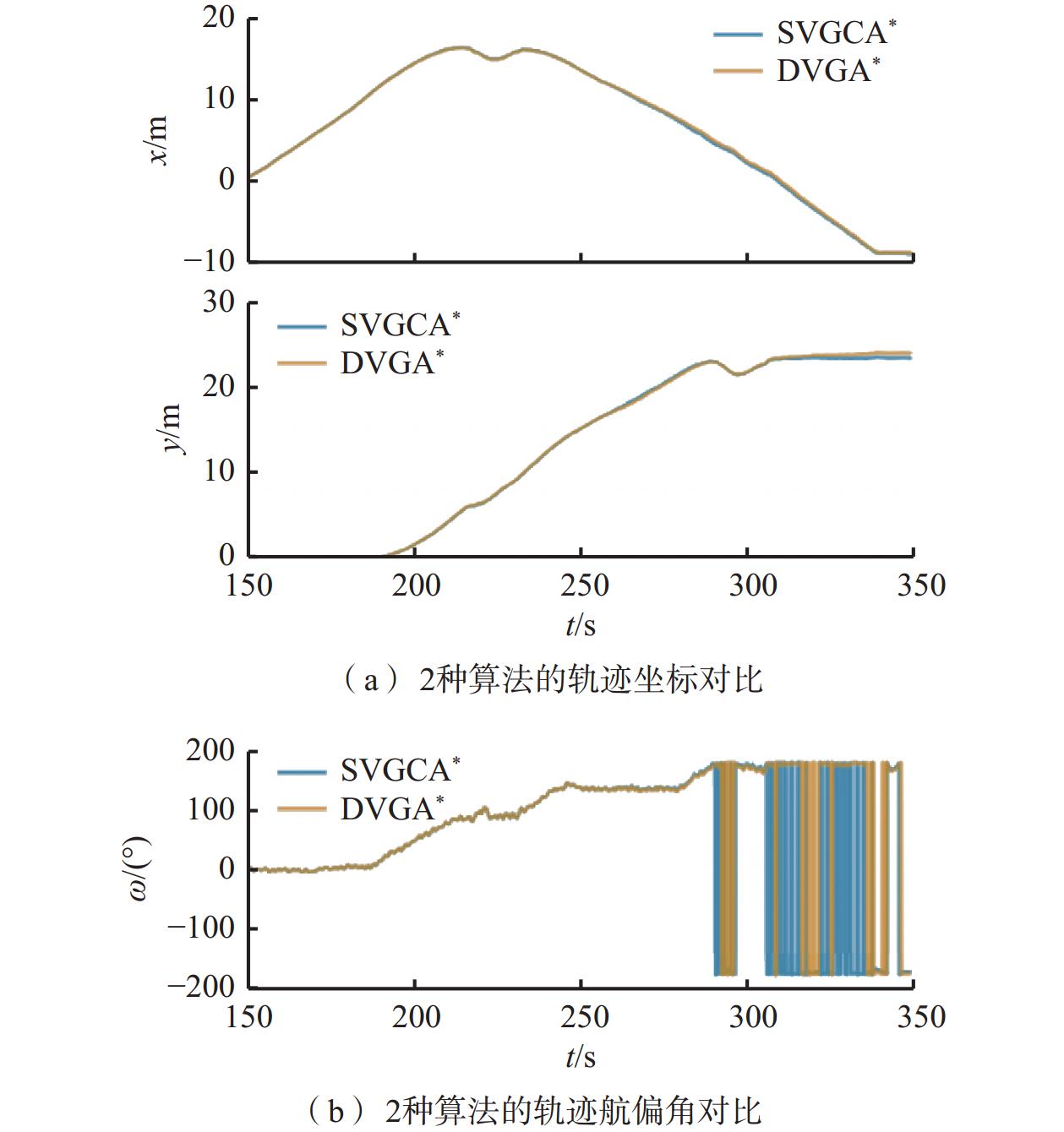
应用SVGCA^*和DVGA^*算法进行井下试验时智能小车轨迹对比如图14所示。可看出2种算法规划出的路径前半段基本吻合，小车在经过较宽巷道和曲率较小的拐弯时都可高效完成行驶和避障；后半段巷道变窄，在躲避动态障碍物B后，SVGCA^*算法规划路径在y方向存在偏移，导致小车行驶不稳定，由图14（b）可明显看出SVGCA^*算法规划路径波动更明显，方向变化更加频繁，不如DVGA^*算法规划路径平滑。

图  14  智能小车井下试验轨迹对比

Figure  14.  Comparison of underground test trajectories of the intelligent car

下载: 全尺寸图片 幻灯片

应用SVGCA^*和DVGA^*算法分别进行10次规划试验并对规划时间和路径长度求平均值，统计成功次数，试验结果见表4。可看出在复杂多变的巷道环境中DVGA^*算法的规划时间和路径长度相比SVGCA^*算法分别减少了11.51%和1.54%，规划的路径可更加高效地到达目标点。由于SVGCA^*算法只考虑了起点到终点穿越线上的障碍物，在井下巷道试验中相比实验室实车实验略微缩小了与DVGA^*算法的差距，但DVGA^*算法规划路径的整体效果仍优于SVGCA^*算法，具有更高的环境适应性和稳定性。

表  4  井下巷道路径规划试验数据对比

Table  4.  Comparison of experimental data on underground roadway path planning

算法	平均规划时间/s	平均路径长度/m	成功次数
SVGCA*	278	87.511	8
DVGA*	246	86.164	9

下载: 导出CSV 

| 显示表格

4.   结论

1） 提出了一种融合DVG和A^*算法的全局路径规划算法DVGA^*。在构建真实环境点云地图的基础上，连接车辆在不同视点下的可视切点动态生成SVG，并在构建过程中搜索相关可视边以发现最优路径。通过仅保留当前扩展节点的后续节点，并丢弃之前步骤中已处理节点的其他分支，删除无关可视边和重复点，使得每次搜索的节点数量减少，有效减少了存储需求，从而降低计算量和执行时间。通过路径平滑算法进一步减少路径节点数量，从而提高路径规划效率。

2） 实验结果表明，与完整可视图+A^*算法、SVG+A^*算法及SVGCA^*算法对比，DVGA^*算法对复杂长距离路径的规划时间最短，平均路径长度分别缩短了10.79 % ，6.26% 和2.86%，对于狭窄、弯曲、存在未知障碍物的井下复杂环境路径规划具有更强的适应性和更高的规划成功率。

3） 井下试验结果表明：在巷道宽度变换区域和躲避静态障碍物时，相比SVGCA^*算法，DVGA^*算法规划的路径更加平滑；躲避动态障碍物时，DVGA^*算法能够及时进行路径纠正，保证了路径规划的时效性和稳定性；在复杂多变的巷道环境中DVGA^*算法的规划时间和路径长度相比SVGCA^*算法分别减少了11.51%和1.54%，具有更高的环境适应性和稳定性。