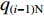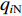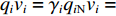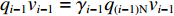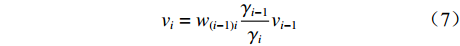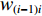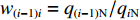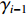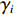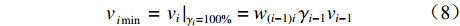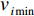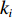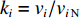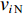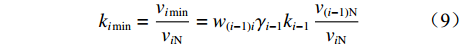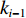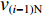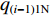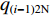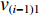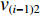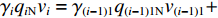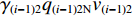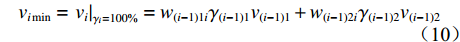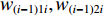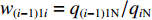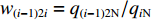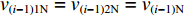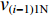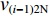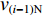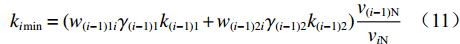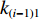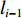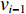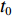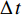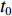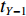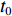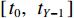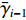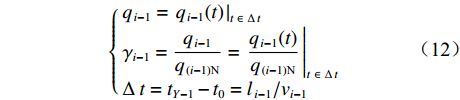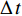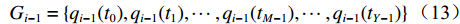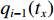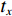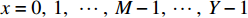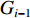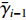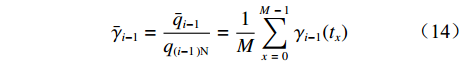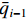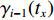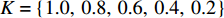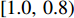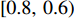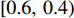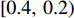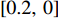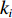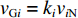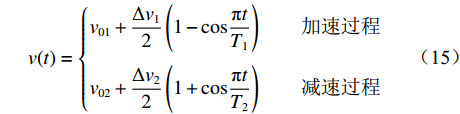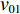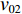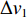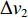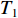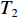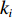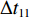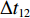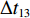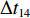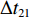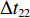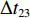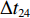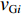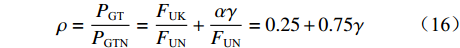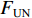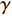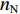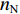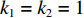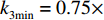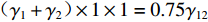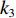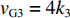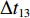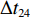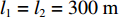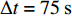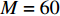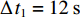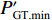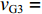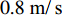Research on energy-saving optimal control method of belt conveyor in coal mine
-
摘要: 由于煤炭生产的不连续性,使带式输送机常常处于空载、轻载及很少达到满载的运行状态,造成电能浪费,同时加剧了设备磨损。目前解决该问题的方法是根据煤流量对带式输送机进行调速控制。但目前的方法较少考虑带式输送机之间煤流的上下游接续关系、煤流量传感器安装位置、检测误差、信息滞后及带速改变过程中的时序关系等。针对上述问题,依据带式输送机驱动功率与运行阻力和带速的关系,得出了带式输送机最优节能运行条件和最佳节电率;根据最优节能运行条件、带式输送机上下游接续方式与物料平衡关系、额定运输质量与额定带速,得出了带式输送机最优节能控制条件下的最小带速与最优带速控制系数;考虑煤流量传感器安装位置、检测误差、信息滞后及带速改变过程中的时序关系等因素,提出了一种带式输送机节能优化控制方法。该方法根据上游带式输送机的煤流量,计算得到最优节能控制条件下下游带式输送机优化节能控制的给定带速变化曲线,依据该曲线实现对下游带式输送机带速的调节。利用搭建的带式输送机模拟节能实验平台,对最佳节电率进行了检验,结果表明:带式输送机在最优节能运行条件下的最佳节电率为20.9%~76.5%,但在实际运输系统中,由于带速不能连续调节,所以不可能达到最优运行工况。将带式输送机节能优化控制方法应用于柠条塔煤矿101号主提升带式输送机控制中,结果表明:该方法实现了煤流的平稳接续,节电率为9.1%~43.9%,节能效果明显。Abstract: Due to the discontinuity of coal production, the belt conveyor is often in the running state of no-load, light load and rarely full load. This causes a waste of electricity and exacerbates the wear and tear of equipment. At present, the method to solve this problem is to control the velocity of belt conveyor according to the information of coal flow. However, the current method seldom considers the connection relationship between the upstream and downstream of the coal flow between the belt conveyors, the installation position of the coal flow sensor, the detection error, the information lag and the timing sequence relationship in the process of belt velocity change. In order to solve the above problems, according to the relationship between driving power, running resistance and belt velocity of belt conveyor, the optimal energy-saving running condition and the optimal energy-saving rate of belt conveyor are obtained. According to the optimal energy-saving running conditions, the relationship between upstream and downstream connection mode of belt conveyor and material balance, rated transportation quality and rated belt velocity, the minimum belt velocity and optimal belt velocity control coefficient under the optimal energy-saving control conditions of belt conveyor are obtained. According to the installation position of the coal flow sensor, the detection error, the information lag and the time sequence relationship of the belt velocity change process, an energy-saving optimal control method of belt conveyor is proposed. According to the coal flow information of the upstream belt conveyor, this method calculates the given curve of the belt velocity change of the downstream belt conveyor under the optimal energy-saving control condition. The adjustment of the belt velocity of the downstream belt conveyor is realized according to the curve. By using the simulated energy-saving experiment platform of belt conveyor, the optimal power saving rate is tested. The results show that the optimal power saving rate of belt conveyor under the optimal energy-saving running condition is 20.9%-76.5%. However, in the actual transportation system, because the belt velocity can not be adjusted continuously, it is impossible to achieve the optimal running condition. The energy-saving optimal control method of belt conveyor is apply to the control of the No. 101 main hoisting belt conveyor in Ningtiaota Coal Mine. And the result shows that this method realizes the smooth connection of coal flow, and the power saving rate is 9.1%-43.9%. The energy saving effect is obvious.
-
0. 引言
带式输送机以其输送能力强、输送距离长、可靠性高和易于集中控制的优势,已经成为煤矿高效生产的主要运输设备[1]。由于煤炭生产的不连续性,使带式输送机常常处于空载、轻载及很少达到满载的运行状态,造成电能浪费,同时加剧了设备磨损[2]。解决这些问题的主要方法是根据检测到的带式输送机载荷对带速进行调节控制,实现“煤多快拉、煤少慢拉”,达到节能和提高运行效率的目的。目前,许多学者对带式输送机调速节能控制方法做了大量研究。文献[3]通过检测驱动电动机负载电流得到负荷大小,从而实现对2部带式输送机的自适应调速控制。文献[4]建立了以煤流量、带速和能耗为变量的节能模型,利用遗传算法和神经网络对模型参数进行优化,得到了煤流量和带速的最优匹配关系,利用模糊控制器实现对2部带式输送机的节能调速控制。文献[5]利用BP神经网络构建了由煤流量、带速和总功率构成的节能优化模型,提出了基于变频调速的带式输送机节能控制策略,实现了对单部带式输送机的优化控制。文献[6]针对煤流量信息滞后问题,利用状态观测器估计输送带张力的变化率和煤流量信息,建立了煤量识别系统,应用模糊推理得到了煤流量与优化带速的匹配关系, 给出了合理的带速,解决了因煤流量检测信号与实时煤量信息不同步导致的带式输送机无法及时提速引发堆煤或溢煤的问题。文献[7]通过载荷检测获取带式输送机的整体载荷和物料分布情况,实现了多级串联带式输送机顺煤流启动。但目前的方法很少考虑带式输送机之间煤流上下游接续关系、煤流量传感器安装位置、检测误差、信息滞后及带速改变过程中的时序关系等对带式输送机调速的影响。针对上述问题,本文分析了带式输送机驱动功率与运行阻力和带速之间的关系,得出了最优节能运行条件和最佳节电率。根据最优节能运行条件和物料平衡关系,综合考虑煤流接续、煤流量检测及带速改变等因素,提出了一种带式输送机节能优化控制方法。将该方法应用于陕煤集团神木柠条塔矿业有限公司(以下简称柠条塔煤矿)101号主提升带式输送机控制中,取得了满意的效果,证明了该方法的可靠性。
1. 带式输送机最优节能运行条件与最佳节电率
在长距离带式输送机稳定运行时,当忽略次要阻力时,其运行阻力可以近似表示为[8]
$$\begin{split} {F_{\text{U}}} \approx & C{F_{\text{H}}} + {F_{{\text{St}}}} = CfLg{\kern 1pt} ({q_{{\text{RO}}}} + {q_{{\text{RU}}}} + 2{q_{\text{B}}})\cos \;\beta+ \hfill \\& g{q_{\text{G}}}(CfL\cos \;\beta + H) \approx {F_{{\text{UK}}}} + A{q_{\text{G}}} \end{split} $$ (1) 式中:C为附加阻力系数;
$ {F_{\text{H}}} $ 和$ {F_{{\text{St}}}} $ 分别为带式输送机的主要阻力和倾斜阻力;f为摩擦因数;L为带式输送机长度;g为重力加速度,$ g = 9.81{\text{ m/}}{{\text{s}}^{\text{2}}} $ ;$ {q_{{\text{RO}}}} $ 和$ {q_{{\text{RU}}}} $ 分别为上下托辊转动部分每米长度质量;$ {q_{\text{B}}} $ 为输送带每米长度质量;$\; \beta $ 为带式输送机安装倾斜角度;$ {q_{\text{G}}} $ 为输送带每米运送的物料质量;H为带式输送机垂直高差;$ {F_{{\text{UK}}}} $ 为空载阻力;A为物料阻力系数。由于生产因素的影响,
$ {q_{\text{G}}} $ 在0~$ {q_{{\text{GN}}}} $ (输送带每米运送物料质量的额定值)之间变化,则带式输送机上物料的填充率可以定义为$$ \gamma = \frac{{{q_{\text{G}}}}}{{{q_{{\text{GN}}}}}} \times 100{\text{% }} $$ (2) 将式(2)代入式(1),得
$$ {F_{\text{U}}} \approx {F_{{\text{UK}}}} + A\gamma {q_{{\text{GN}}}} \approx {F_{{\text{UK}}}} + \alpha \gamma $$ (3) 式中α为常数,
$ \alpha = A{q_{{\text{GN}}}} $ 。根据带式输送机驱动功率与驱动力和运行速度之间的关系,当带式输送机匀速运行时,驱动滚筒所需的功率为
$$ {P_{{\text{GT}}}} = {F_{\text{U}}}v $$ (4) 式中
$ {v} $ 为带速。可见,在运行阻力不变的条件下,降低带式输送机带速可减小带式输送机驱动功率。
带式输送机节能优化控制就是在不影响运输生产的前提下,使驱动功率最小。则目标函数为
$$\begin{aligned} & \mathrm{min}{P}_{\text{GT}}=f(v\text{,}\gamma )\\& {\rm{ s.t. }}\;\; v={{v}_{\mathrm{min}}|}_{\gamma =100{\text{%}}} \end{aligned}$$ (5) 实现最优节能控制就是通过调节带式输送机带速,使其在满载(
$ \gamma = 100{\text{% }} $ )状态下以最小带速($ {v_{\min }} $ )运行,此时驱动功率最小。设带式输送机在不同填充率
$ {\gamma _j} $ ($ {\gamma _j} $ 为第j次获取的填充率,$ j = 1{\kern 1pt} ,\;\;2{\kern 1pt} ,\;\; \cdots ,\;r $ ,r为获取次数)下以额定带速$ {v_{\text{N}}} $ 运行时的最大驱动功率为$ {P_{{\text{GT}}{\text{.max}}}} $ ,改变带速使带式输送机以最优节能方式运行时的驱动功率为$ {P_{{\text{GT}}{\text{.min}}}} $ ,定义这2个驱动功率之差与最大驱动功率之比为不同填充率$ {\gamma _j} $ 下的最佳节电率,即$$ {\lambda _{j.\max }} = \frac{{{P_{{\text{GT}}{\text{.max}}}} - {P_{{\text{GT}}{\text{.min}}}}}}{{{P_{{\text{GT}}{\text{.max}}}}}} \times 100{\text{% } }$$ (6) 式中
$ {\lambda _{j.\max }} $ 为不同填充率下的最佳节电率。2. 最优控制带速确定
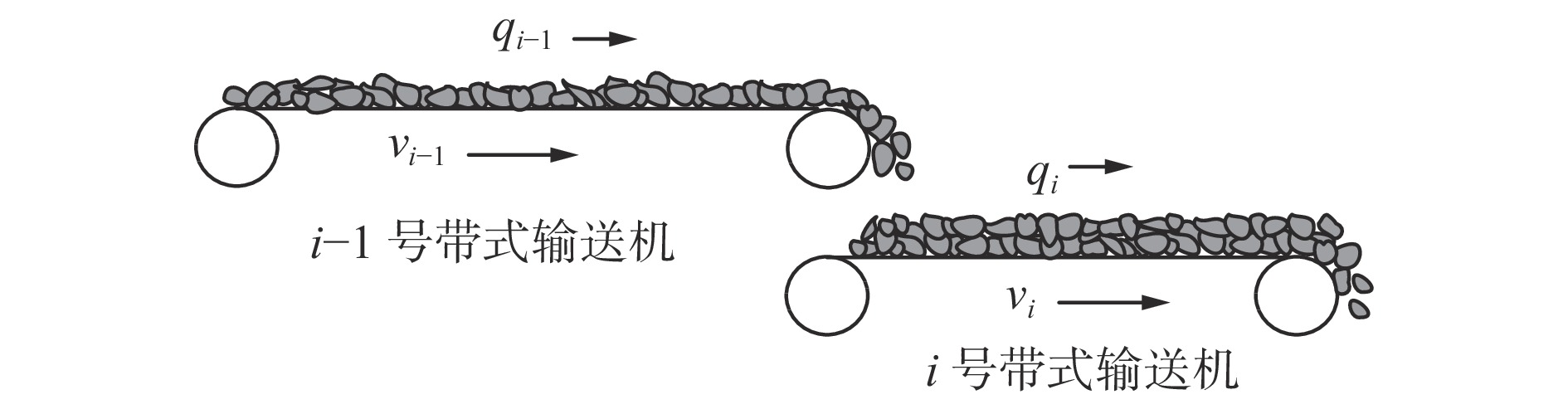
在实际运输系统中,带式输送机之间均以串联接续的方式进行煤炭运送,任一部带式输送机的填充率和带速的改变都会影响下游带式输送机的填充率和带速。运输系统中带式输送机单入串联接续如图1所示。
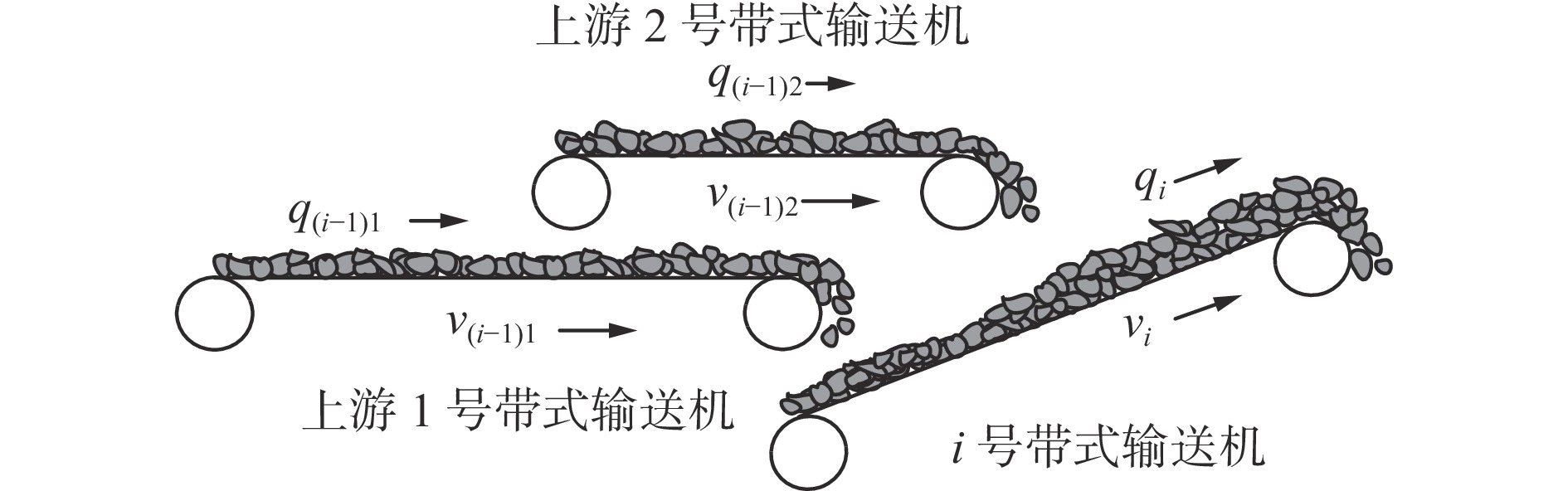
$ {q_{i - 1}} $ ,$ {v_{i - 1}} $ 和$ {q_i} $ ,$ {v_i} $ 分别为i−1号(上游)和i号(下游)带式输送机的实时煤流量(每米输送带上的煤炭质量)和带速,当运输系统运行时,上游带式输送机上的来煤就落入下游带式输送机上,构成串联接续关系。设i−1号和i号带式输送机的额定煤流量分别为
$ {q_{(i - 1){\text{N}}}} $ 和$ {q_{i{\text{N}}}} $ ,根据物料平衡关系(即${q_i}{v_i} = {\gamma _i}{q_{i{\text{N}}}}{v_i} = $ $ {q_{i - 1}}{v_{i - 1}} = {\gamma _{i - 1}}{q_{(i - 1){\text{N}}}}{v_{i - 1}}$ ),可得i号带式输送机带速:$$ {v_i} = {w_{(i - 1)i}}\frac{{{\gamma _{i - 1}}}}{{{\gamma _i}}}{v_{i - 1}} ^{ } $$ (7) 式中:
$ {w_{(i - 1)i}} $ 为上游带式输送机相对于下游带式输送机的运能系数,${w_{(i - 1)i}} = {q_{(i - 1){\text{N}}}}/{q_{i{\text{N}}}}$ ;$ {\gamma _{i - 1}} $ ,$ {\gamma _i} $ 分别为i−1号(上游)和i号(下游)带式输送机的填充率。根据最优节能运行条件,由式(7)可得
$$ v{\kern 1pt} _{i\min }^{\kern 1pt} \, = {\left. {{v_i}{\kern 1pt} } \right|_{{\gamma _i} = 100{\text{%}} }} = {w_{(i - 1)i}}\,{\gamma _{i - 1}}{v_{i - 1}} ^{ } $$ (8) 式中
$ v{\kern 1pt} _{i\min }^{\kern 1pt} $ 为i号带式输送机填充率为1时的最小带速。由于煤炭的散料特性,为了避免带速变化引起的溢煤或堆煤事故,带速不能连续调节,只能以台阶式变化。为此引入带速控制系数
${k_i} $ ($ {k_i} = {v_i}/{v_{i{\kern 1pt} {\text{N}}}} $ ,$ {v_{i{\kern 1pt} {\text{N}}}} $ 为i号带式输送机的额定带速)。结合式(8)可得i号带式输送机的最优带速控制系数:$$ {k_{i\min }} = \frac{{{v_{i\min }}}}{{{v_{i{\rm{N}}}}}} = {w_{(i - 1)i}}{\gamma _{i - 1}}{k_{i - 1}}\,\frac{{{v_{(i - 1 ){\text{N}}}}}}{{{v_{i{\rm{N}}}}}} ^{ } $$ (9) 式中
${k_{i-1 }} $ ,${v_{(i - 1 ){\text{N}} } }$ 分别为i−1号带式输送机带速控制系数和额定带速。带式输送机双入串联接续如图2所示,当运输系统运行时,上游带式输送机(1号、2号)的来煤就落入下游带式输送机,构成双入串联接续关系。
设上游1号、2号带式输送机额定煤流量、填充率、带速分别为
$ {q_{(i - 1)1{\text{N}}}} $ 和$ {q_{(i - 1)2{\text{N}}}} $ 、$ {\gamma _{(i - 1)1}} $ 和$ {\gamma _{(i - 1)2}} $ 、${v_{(i - 1)1}} $ 和${v_{(i - 1)2}} $ ,由物料平衡关系(即${\gamma _i}{q_{i{\text{N}}}}{v_i} = {\gamma _{(i - 1)1}}{q_{(i - 1)1{\text{N}}}}{v_{(i - 1)1}} + $ $ {\gamma _{(i - 1)2}}{q_{(i - 1)2{\text{N}}}}{v_{(i - 1)2}}$ ),可得最优节能运行条件下的带速:$$ v _{i\min } = {\left. {{v_i} } \right|_{{\gamma _i} = 100{\text{%}} }} = {w_{(i - 1) 1i}} {\gamma _{( i - 1 ) 1}}{v_{( i - 1 ) 1}} + {w_{(i - 1 ) 2i}} {\gamma _{( i - 1 ) 2}}{v_{( i - 1 ) 2}} ^{ } $$ (10) 式中
${w_{(i - 1)1i}},{w_{(i - 1)2i}} $ 分别为上游1号、2号带式输送机相对于i号带式输送机的运能系数,$ {w_{(i - 1)1i}} = {q_{(i - 1)1{\text{N}}}}/{q_{i{\text{N}}}} $ ,$ {w_{(i - 1)2i}} = {q_{(i - 1)2{\text{N}}}}/{q_{i{\text{N}}}} $ 。若
$ {v_{(i - 1)1{\text{N}}}} = {v_{(i - 1)2{\text{N}}}} = {v_{(i - 1){\text{N}}}} $ (${v_{(i - 1)1{\text{N}}}} $ ,${v_{(i - 1)2{\text{N}}}} $ 分别为上游1号、2号带式输送机额定带速,${v_{(i - 1){\text{N}}}} $ 为上游带式输送机额定带速),由式(10)可得i号带式输送机的最优带速控制系数:$$ {k_{i\min }} = ({w_{(i - 1) 1i}} {\gamma _{( i - 1 ) 1}}{k_{( i - 1 ) 1}} + {w_{(i - 1 ) 2i}} {\gamma _{( i - 1 ) 2}}{k_{( i - 1 ) 2}})\frac{{{v_{(i - 1) {\text{N}}}}}}{{{v_{i{\text{N}}}}}}\;\;\; $$ (11) 式中
${k_{( i - 1 ) 1}} $ ,${k_{( i - 1 ) 2}} $ 分别为上游1号、2号带式输送机带速控制系数。3. 节能优化控制方法
根据最优节能运行条件和物料平衡关系,可得最优节能控制条件下带式输送机的最优控制带速给定值。但受煤炭的散料特性、带式输送机上下游接续、煤流量传感器安装位置造成的信息滞后、检测误差及带速改化过程中的时序关系等因素的影响,带式输送机不可能以最优控制带速(
$ {v_{i\min }} $ )运行,否则,会造成溢煤或堆煤事故。为了实现调速过程中煤流平稳接续,根据带式输送机最优节能运行条件,并考虑上述因素,以i号带式输送机为例,研究带式输送机节能优化控制方法的实现。3.1 煤流量信息检测
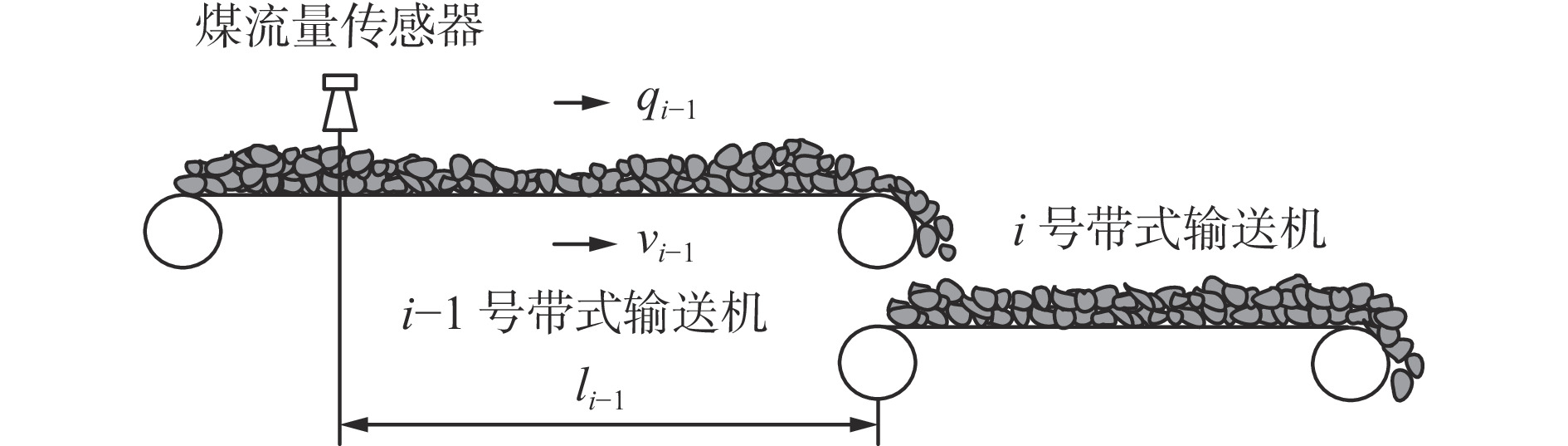
设上游(i−1号)带式输送机的煤流量传感器安装位置距机头距离为
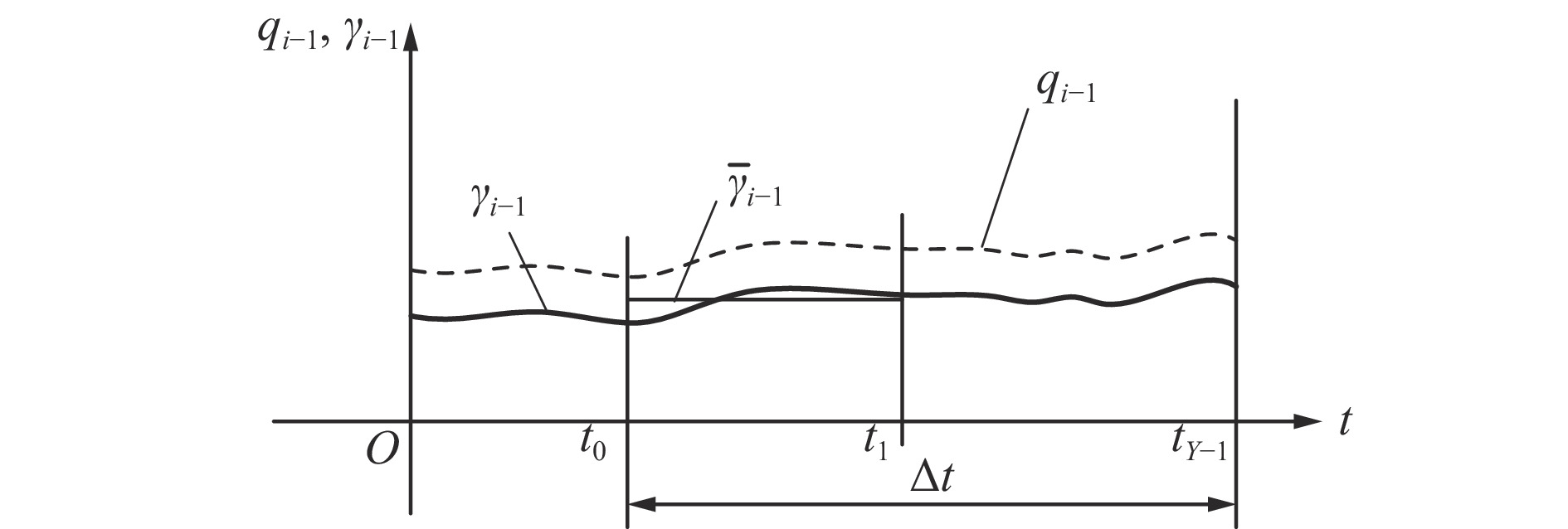
$ {l_{i - 1}} $ ,其带速为$ {v_{i - 1}} $ ,煤流量信息检测如图3所示。设煤流量传感器读取数据的时间为t,从
$ {t_0} $ 时刻开始读取数据,经过$ \Delta \,t $ ($ {t_0} $ −$ {t_{Y{{ - }}1}} $ 时刻,Y为煤流量传感器读取的实时数据个数)时段,$ {t_0} $ 时刻检测的煤流(数据)到达机头,则在$[\,{t_0},\;\;{t_{Y{{ - }}1}}\,]$ 区间内i−1号带式输送机的煤流量与填充率的关系如图4(图中$ {\bar \gamma _{i - 1}} $ 为i−1号带式输送机的平均填充率)所示,表达式如下:$$ \left\{ {\,\begin{array}{l} {{q_{\,i - 1}} = {{\left. {{q_{\,i - 1}}(t)\,} \right|}_{t\,{\kern 1pt} \in {\kern 1pt} {\kern 1pt} \Delta {\kern 1pt} t}}\;\,\,\quad \;\;\;} \\ {{\gamma _{i - 1}} = \dfrac{{{q_{\,i - 1}}}}{{{q_{\,(i - 1){\text{N}}}}}} = {{\left. {\dfrac{{{q_{\,i - 1}}(t)}}{{{q_{\,(i - 1){\text{N}}}}}}\,} \right|}_{t{\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} \Delta {\kern 1pt} t}}} \\ {\Delta {\kern 1pt} \,t = {t_{Y{{ - }}1}} - {t_0} = {l_{{\kern 1pt} i - 1}}/{v_{i - 1}}\;\;\;} \end{array}} \right. ^{ } $$ (12) 在
$ \Delta \,t $ 时段内,设煤流量传感器读取了Y个实时数据,则i−1号带式输送机上煤流量的实时数据集合为$$ {G_{i - 1}} = \{ {q_{i - 1}}({t_0}),{q_{i - 1}(t_1)}, \cdots , {q_{i - 1}} ({t_{M {{ - }}1}}), \cdots , {q_{i - 1}}({t_{Y - 1}}) \} \; $$ (13) 式中
$ \;{q_{i - 1}}({t_x}) $ 为i−1号带式输送机在任意时刻$ \;{t_x} $ 的煤流量,$\,x = 0,\;1,\;\; \cdots ,\; M - 1,\; \cdots ,\;Y - 1$ (M为任意时刻采集的数据个数)。在运输系统运行时,集合
$ {G_{i - 1}} $ 中的Y个数据是不断刷新的。为了消除检测干扰,求取M个数据的平均值(滤波),即以平均填充率$ {\bar \gamma _{i - 1}} $ 作为下游带式输送机带速改变的依据。$$ {\bar \gamma _{i - 1}} = \frac{{{{\bar q}_{i - 1}}}}{{{q_{(i - 1{\kern 1pt} ){\text{N}}}}}} = \frac{1}{M}\sum\limits_{x{\kern 1pt} {\kern 1pt} = \,{\kern 1pt} 0}^{M{\kern 1pt} {\kern 1pt} {{ - }}{\kern 1pt} 1} {\,{\gamma _{i - 1}}({t_x})} ^{ } $$ (14) 式中:
${{{{\bar q}_{i - 1}}}} $ 为i−1号带式输送机的平均煤流量;${\gamma _{i - 1}}({t_x})$ 为i−1号带式输送机在任意时刻tx的填充率。3.2 优化控制给定带速与带速改变时序确定
为了防止溢煤或堆煤事故,带速不能连续变化,即最优带速控制系数
$ {k_{i\min }} $ 必须为离散值。假设$ {k_{i\min }} $ 的集合$ K = \left\{ {{\kern 1pt} 1.0,\;0.8,\;0.6,\;0.4,\;0.2\,} \right\} $ ,所对应的区间分别为$ [1.0,\;0.8) $ 、$ [0.8,\;0.6) $ 、$ [0.6,\;0.4) $ 、$ [0.4,\;0.2) $ 和$ [0.2,\;0] $ 。对于带式输送机单入和双入串联接续方式,可根据式(9)和式(11)分别求出最优带速控制系数$ {k_{i\min }} $ ,判断其落入的区间,并取该区间的上限值作为优化带速控制系数$ {k_i} $ ,进而求出给定带速$ {v_{{\text{G}}i}} = {k_i}{v_{i{\text{N}}}} $ 。考虑带式输送机的动态特性[9-10],其带速的改变分为加速(启动)或减速(制动)过程,带速变化表达式为
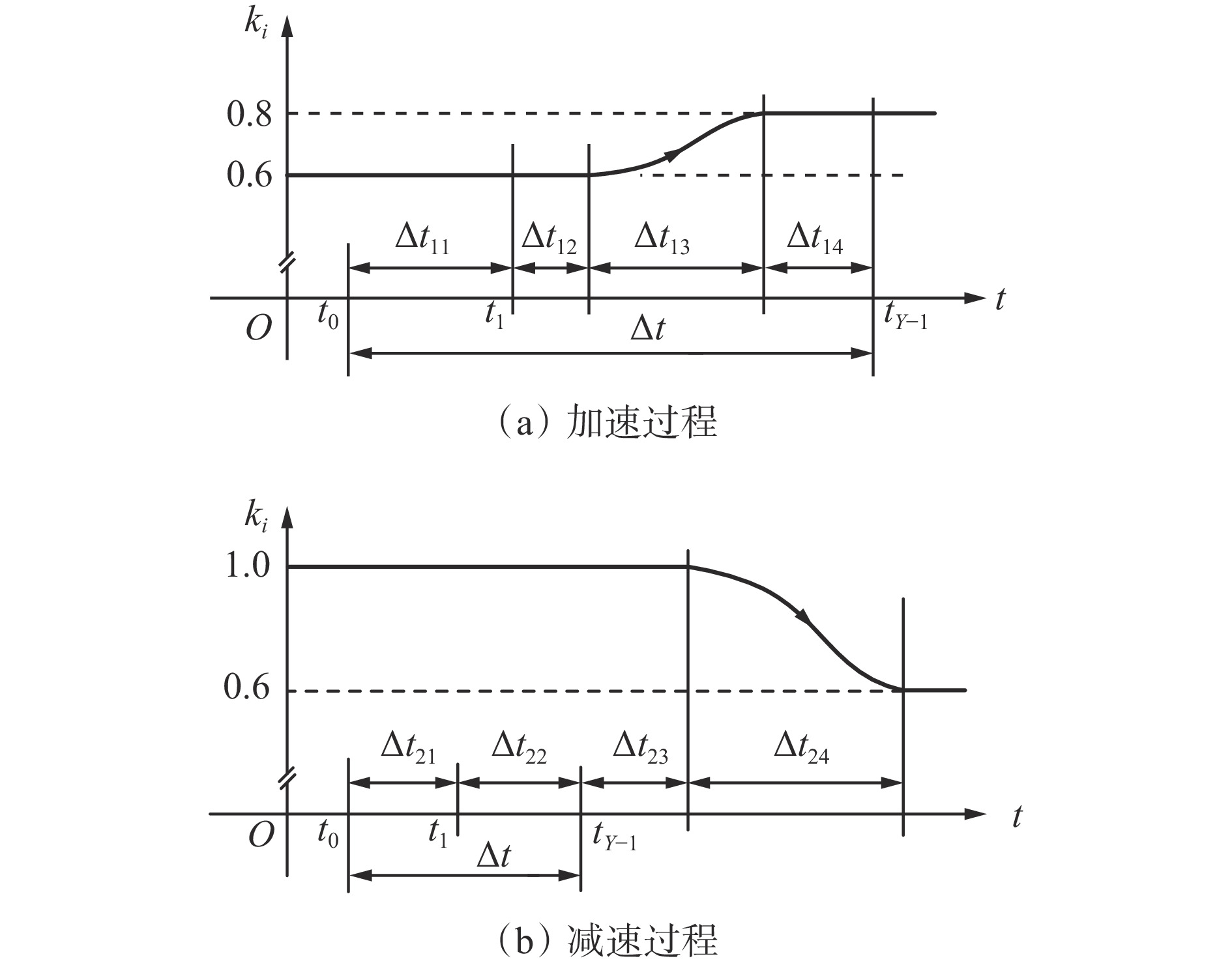
$$ v(t)=\left\{ \begin{array}{l}{v}_{01}+\dfrac{\Delta {v}_{1}}{2}\left(1-\mathrm{cos}\dfrac{\text{π} t}{{T}_{1}}\right)\qquad 加速过程\\ {v}_{02}+\dfrac{\Delta {v}_{2}}{2}\left(1+\mathrm{cos}\dfrac{\text{π} t}{{T}_{2}}\right)\qquad 减速过程\end{array} ^{ } \right.$$ (15) 式中:
$ {v_{01}} $ 和$ {v_{02}} $ 为原有带速;$ \Delta {v_1} $ 和$ \Delta {v_2} $ 为带速改变量;$ {T_1} $ 和$ {T_2} $ 为加速与减速段时长。考虑到煤流检测信息的滞后性,为了避免由于带速改变引起的溢煤或堆煤事故,实现煤流平稳接续,启动过程必须超前,制动过程必须滞后;同时依照设定的带速控制系数
$ {k_i} $ ,得到在加速与减速过程中给定带速(控制系数)的曲线,如图5所示。图中$\Delta {t_{11}}$ ,$\Delta {t_{12}}$ ,$\Delta {t_{13}}$ ,$\Delta {t_{14}}$ 分别为加速过程中的检测滤波时段、延时时段、加速时段和安全延时时段;$\Delta {t_{21}}$ ,$\Delta {t_{22}}$ ,$\Delta {t_{23}}$ ,$\Delta {t_{24}}$ 分别为减速过程中的检测滤波时段、延时时段、安全延时时段和减速时段。3.3 最优节能控制方法
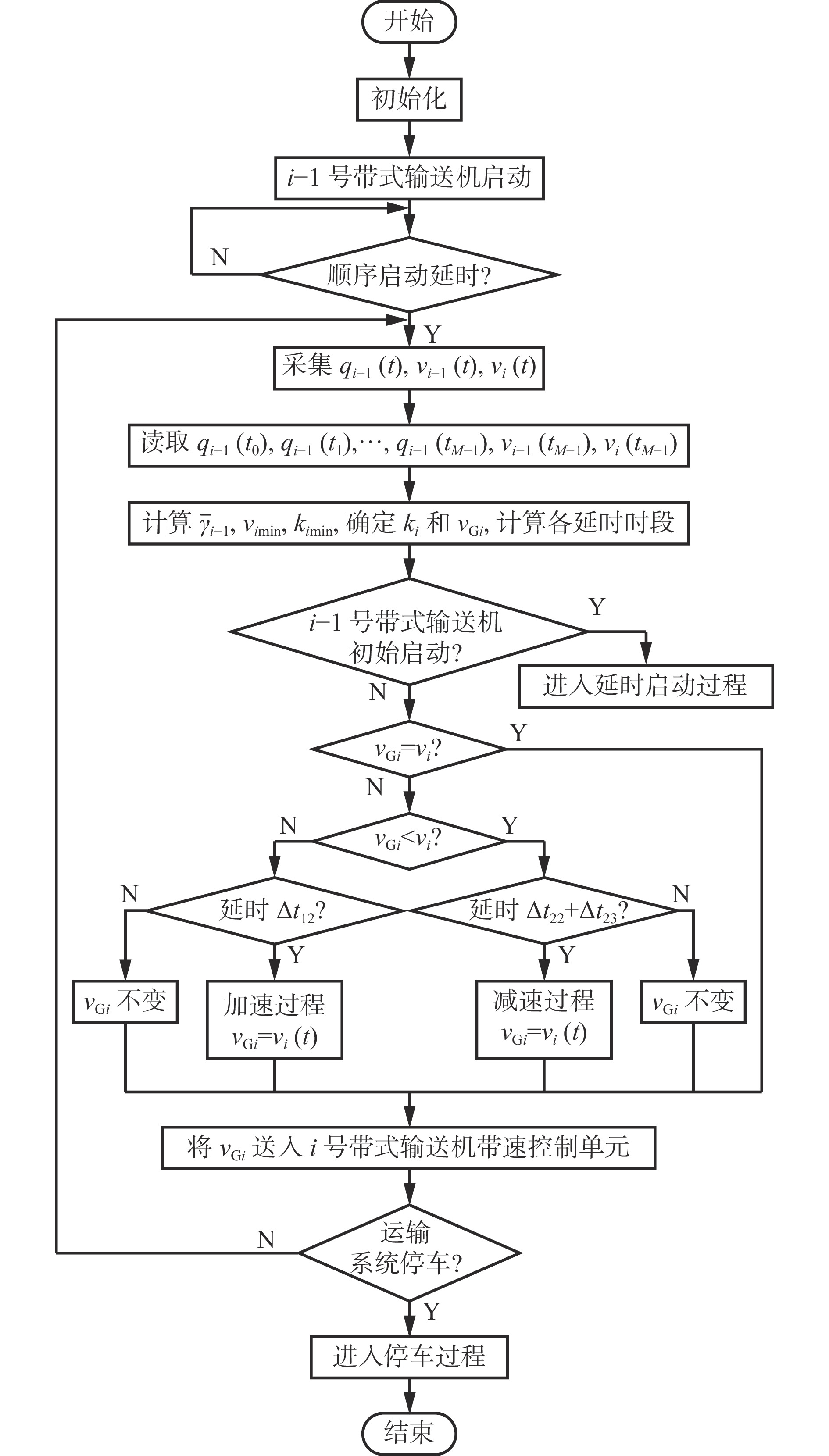
根据上述分析,运输系统中i号带式输送机节能优化控制流程如图6所示。
初始化是输入基本参数,如煤流量、带速、运能系数及带速控制系数与其区间等;系统依次启动,在i−1号带式输送机启动结束后顺序启动延时,延时结束后采集各参数并读取数据,计算并确定i号带式输送机的给定带速
$ {v_{{\text{G}}i}} $ 和各时段延时;若为初始启动则根据给定带速和延时进入启动过程,否则将给定带速与当前实时带速进行比较,若相等则速度不变,否则延时不变,延时到则分别进入加速或减速过程,并将得到的给定带速送入i号带式输送机带速控制单元,对i号带式输送机进行带速调节,运输系统停车前依次循环。4. 实验与应用
4.1 带式输送机最优节能实验
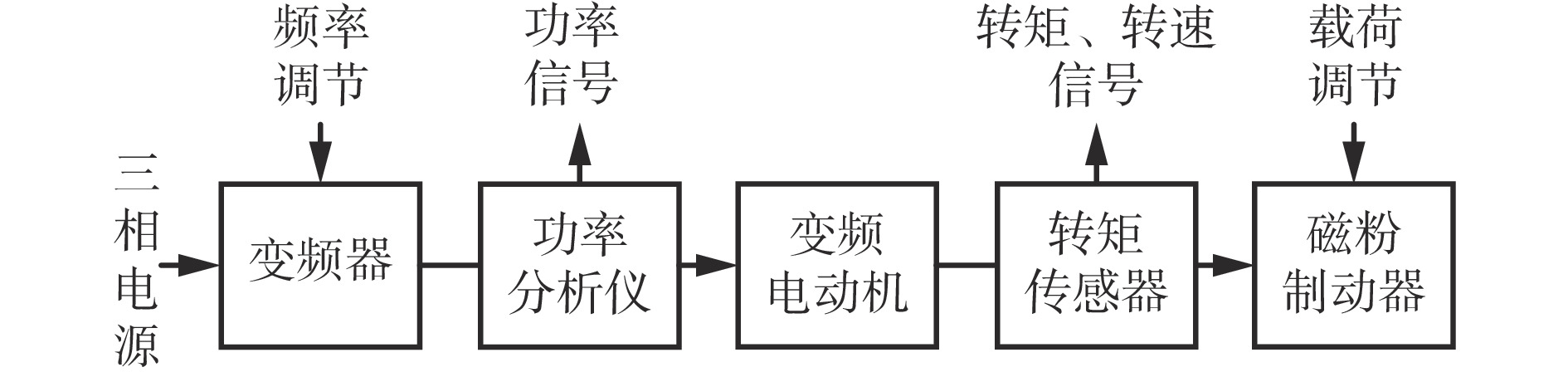
为了检验带式输送机在最优节能运行条件下的最佳节电率,搭建了由变频器、功率分析仪、变频电动机、转矩传感器和磁粉制动器组成的带式输送机模拟节能实验平台,如图7所示。
变频器型号为DCS550−01−12A−4(5.5 kW),功率分析仪型号为PA3000,变频电动机型号为YZP132M2−6(功率为3.7 kW和转速为912 r/min),转矩传感器型号为ZJ−100,磁粉制动器型号为CZ−5(力矩为0~50 N·m,可调)。
根据文献[11-12]的数据,计算出带式输送机空载阻力与额定运行阻力的比值分别为21.9%、20.3%和29.7%,为了模拟实验计算方便,本文设带式输送机空载阻力与额定运行阻力的比值为25%,由式(3)和式(4)可得驱动电动机负载率与填充率的关系:
$$ \rho = \frac{{{P_{{\text{GT}}}}}}{{{P_{{\text{GTN}}}}}} = \frac{{{F_{{\text{UK}}}}}}{{{F_{{\text{UN}}}}}} + \frac{{\alpha \gamma }}{{{F_{{\text{UN}}}}}} = 0.25 + 0.75\gamma ^{ } $$ (16) 式中:
$\;\rho $ 为驱动电动机负载率;${P_{{\text{GTN}}}} $ 为带式输送机额定驱动功率;${F_{{\text{UN}}}} $ 为带式输送机额定运行阻力。设填充率
$ \gamma $ 分别为0,0.2,0.4,0.6,0.8,1.0,由式(16)求出对应的负载率并通过磁粉制动器加载,取转速n的控制系数依次为0.2,0.4,0.6,0.8,1.0,分别记录在不同填充率和不同转速下电动机的驱动功率,见表1。其中$ {n_{\text{N}}} $ 为电动机额定转速,$ {n_{\text{N}}} $ 对应列数据为不同填充率下非节能运行模式下电动机的驱动功率,对角数据(粗体)为最优运行状态下电动机的驱动功率,右下角部分(斜体)为不允许出现的溢煤状态下的电动机驱动功率。由式(6)和表1中的数据可计算出不同填充率下的最佳节电率,见表2。由表2可看出,带式输送机在最优节能运行条件下的最佳节电率为20.9%~76.5%。但是,在实际运输系统中,由于带速不能连续调节,所以不可能达到最优运行工况。
表 1 不同填充率和转速下的电动机驱动功率Table 1. Driving powers of motor at different filling rate and rotate speed$ \gamma $ 驱动功率/W $ {n_{\text{N}}} $ $ 0.8{n_{\text{N}}} $ $ 0.6{n_{\text{N}}} $ $ 0.4{n_{\text{N}}} $ $ 0.2{n_{\text{N}}} $ 0 1541.7 1247.8 957.8 668.9 390.1 0.2 2114.3 1678.1 1284.5 893.4 497.8 0.4 2406.9 1931.8 1481.7 968.6 575.1 0.6 2977.0 2389.1 1806.2 1236.7 698.7 0.8 3520.9 2785.0 2092.5 1461.7 871.6 1.0 4111.1 3321.6 2508.7 1744.6 1132.4 表 2 不同填充率下的最佳节电率Table 2. Optimal power saving rate under different filling rate$ \gamma $ 0 0.2 0.4 0.6 0.8 ${\lambda _{\max } } /{\text{%}}$ 74.7 76.5 59.8 39.3 20.9 4.2 柠条塔煤矿主提升带式输送机节能优化控制
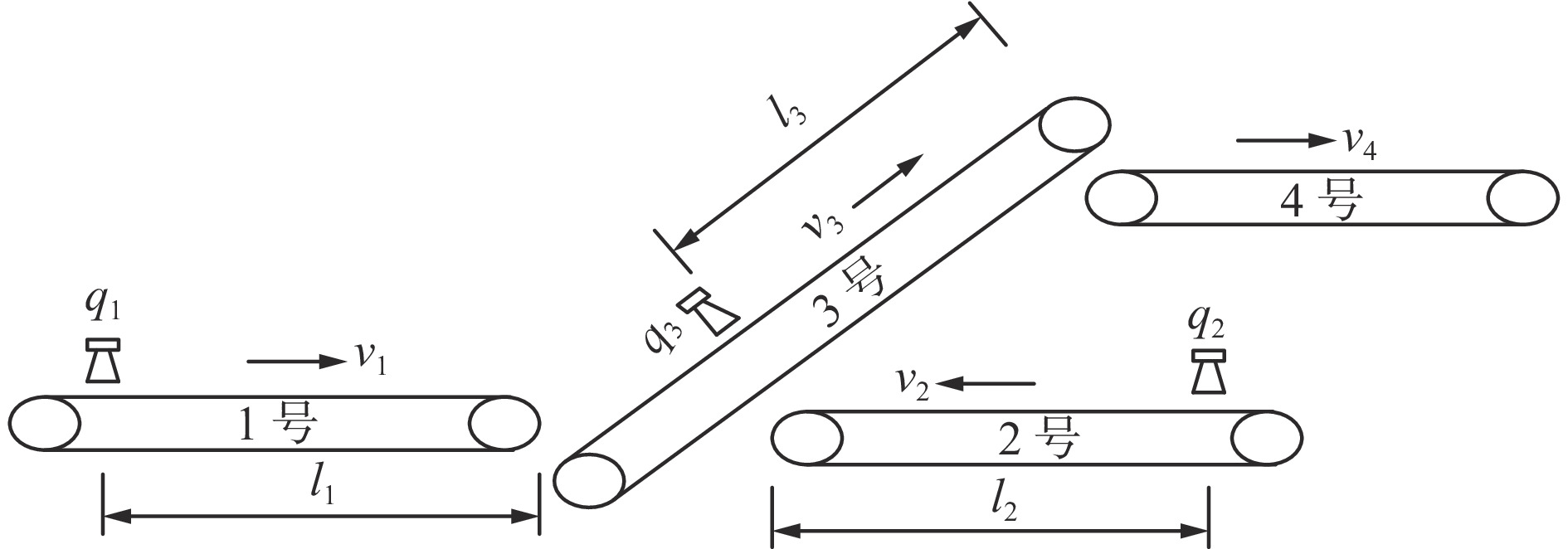
柠条塔煤矿主运输系统结构如图8所示。其中1号—4号带式输送机分别为北翼N3−1、南翼S3−1、主提升101号和栈桥102号带式输送机,基本参数见表3。1号、2号带式输送机以双入串联接续方式将煤炭送入3号带式输送机,3号和4号带式输送机为单入串联接续方式。
表 3 带式输送机基本参数Table 3. Basic parameters of belt conveyors基本参数 带式输送机 1号 2号 3号 4号 长度/m 2500 2000 2000 160 装机功率/kW 1500 1500 3000 132 输送量/(t·h−1) 3000 3000 4000 4000 额定带速/(m·s−1) 4.0 4.0 4.0 4.0 煤流量测距/m l1=300 l2=300 l3=280 — 下面以3号带式输送机为对象对其进行节能优化控制应用。设计了柠条塔煤矿主提升带式输送机优化节能控制系统,其硬件平台利用已有的胶带运输集中控制系统[13],即基于工业以太网的AB Controllogix1756 系列 PLC系统。1号—3号带式输送机的煤流量和带速检测选用ICS−ST型矿用电子胶带秤,煤流量和带速信息通过各自连接的PLC控制分站、以太网交换机和环网上传至数据服务器和控制主机,控制主机通过数据处理,计算出给定带速,将给定带速信息送至3号带式输送机的控制分站,调速控制采用PID控制算法。
设1号和2号带式输送机以额定带速运行,其带速控制系数
$ {k_1} = {k_2} = 1 $ ;由表3参数和式(11)可得3号带式输送机的最优带速控制系数$k{}_{3\mathrm{min}}^{}=0.75\times $ $ ({\gamma }_{1}+{\gamma }_{2})\times 1\times 1=0.75 {\gamma }_{12}$ ,然后判断其落入集合K所对应的区间,并取上限值作为最优带速控制系数$ {k_3} $ ,得到3号带式输送机给定带速$ {v_{{\text{G}}3}} =4 {k_3} $ 。根据文献[13],3号带式输送机的全速启动时长为50 s,设全速停车时长也为50 s,因为离散带速被划分为5级,则每一级时长为10 s,由此可计算出不同加速或减速时段的时长
$ \Delta {t_{13}} $ 和$ \Delta {t_{24}} $ 。由
${l_1} = {l_2} = 300{\text{ m}}$ ,可得$ \Delta t = 75{\kern 1pt} {\kern 1pt} {\text{s}} $ ;设带速控制周期为200 ms,取式(13)中的$ M = 60 $ ,得$ \Delta {\kern 1pt} {t_1} = 12{\kern 1pt} {\kern 1pt} {\text{s}} $ ,可以计算出加速与减速过程各时段的时长,表4分别给出了1个加速和减速过程接续时段的数据。加速和减速过程中原有带速分别为0.8 m/s和3.2 m/s,根据上游1号、2号带式输送机的煤流量信息,需要将3号带式输送机带速分别增大或减小到3.2 m/s或2.4 m/s。表 4 加速与减速过程接续时段Table 4. Connection time interval in acceleration and deceleration process加速过程(0.8~3.2 m/s) 减速过程
(3.2~2.4 m/s)时段 时长/s 时段 时长/s $ \Delta {t_{11}} $ 12 $ \Delta {t_{21}} $ 12 $ \Delta {t_{12}} $ 23 $ \Delta {t_{22}} $ 63 $ \Delta {t_{13}} $ 30 $ \Delta {t_{23}} $ 10 $ \Delta {t_{14}} $ 10 $ \Delta {t_{24}} $ 10 在主提升带式输送机优化节能控制系统硬件平台基础上,根据图6的控制流程和实际参数完成3号带式输送机节能优化控制系统软件的编程与调试,实现了根据上游1号和2号带式输送机的实时煤流量和带速信息对3号带式输送机进行调速节能优化控制与煤流的平稳接续。对3号带式输送机在非节能和节能优化控制2种运行模式及不同填充率下的驱动功率进行统计,结果见表5。表中
${P'_{ {\text{GT} }{\text{.min} } } } $ 为节能优化控制下的驱动功率。表 5 不同工况下驱动功率统计Table 5. Powers statistics under different working conditions${\gamma _3}$ 驱动功率/kW $ {k_3} $ $\lambda / {\text{%}}$ $ {P_{{\text{GT}}.{\text{max}}}} $ ${P'_{ {\text{GT} }{\text{.min} } } }$ 0 981 364 0.2 62.9 (0,0.2] 1335 749 0.2 43.9 (0.2,0.4] 1658 1201 0.4 27.6 (0.4,0.6] 2036 1634 0.6 19.7 (0.6,0.8] 2397 2178 0.8 9.1 (0.8,1.0] 2799 2799 1.0 − 在表5中,当3号带式输送机空载(
$ {\gamma _3} = 0 $ ,${v_{{\text{G3}}}} = $ $ 0.8{\text{ m/}}{\kern 1pt} {\kern 1pt} {\text{s}}$ )时,节电率为62.9%;在不同填充率区间和对应的优化带速控制条件下,节电率为9.1%~43.9%。运行结果表明,本文提出的节能优化控制方法实现了煤流的平稳接续,节能效果明显。5. 结论
(1) 从带式输送机的运行阻力出发,可得其驱动功率与运送物料的填充率和带速有关,最优节能控制目标是调节带速,使带式输送机在满载状态下以最小带速运行,此时驱动功率最小,由此可获得节能优化控制的最佳节电率。利用搭建的带式输送机模拟节能实验平台,实验得出带式输送机的最佳节电率为20.9%~76.5%。
(2) 根据最优节能运行条件、带式输送机上下游接续方式与物料平衡关系、额定运输质量与额定带速,推导得出带式输送机最优节能控制条件下的最小带速与最优带速控制系数;考虑煤流量传感器安装位置、检测误差、信息滞后及带速改变过程中的时序关系等因素,提出了一种带式输送机节能优化控制方法。该方法根据上游带式输送机的煤流量,计算得出最优节能控制条件下下游带式输送机优化节能控制的给定带速变化曲线,由此可实现下游带式输送机带速调节。
(3) 带式输送机节能优化控制方法已应用于柠条塔煤矿101号主提升带式输送机控制中,实现了对带式输送机的优化节能控制,节能效果明显,节电率为9.1%~43.9%。
-
表 1 不同填充率和转速下的电动机驱动功率
Table 1 Driving powers of motor at different filling rate and rotate speed
$ \gamma $ 驱动功率/W $ {n_{\text{N}}} $ $ 0.8{n_{\text{N}}} $ $ 0.6{n_{\text{N}}} $ $ 0.4{n_{\text{N}}} $ $ 0.2{n_{\text{N}}} $ 0 1541.7 1247.8 957.8 668.9 390.1 0.2 2114.3 1678.1 1284.5 893.4 497.8 0.4 2406.9 1931.8 1481.7 968.6 575.1 0.6 2977.0 2389.1 1806.2 1236.7 698.7 0.8 3520.9 2785.0 2092.5 1461.7 871.6 1.0 4111.1 3321.6 2508.7 1744.6 1132.4 表 2 不同填充率下的最佳节电率
Table 2 Optimal power saving rate under different filling rate
$ \gamma $ 0 0.2 0.4 0.6 0.8 ${\lambda _{\max } } /{\text{%}}$ 74.7 76.5 59.8 39.3 20.9 表 3 带式输送机基本参数
Table 3 Basic parameters of belt conveyors
基本参数 带式输送机 1号 2号 3号 4号 长度/m 2500 2000 2000 160 装机功率/kW 1500 1500 3000 132 输送量/(t·h−1) 3000 3000 4000 4000 额定带速/(m·s−1) 4.0 4.0 4.0 4.0 煤流量测距/m l1=300 l2=300 l3=280 — 表 4 加速与减速过程接续时段
Table 4 Connection time interval in acceleration and deceleration process
加速过程(0.8~3.2 m/s) 减速过程
(3.2~2.4 m/s)时段 时长/s 时段 时长/s $ \Delta {t_{11}} $ 12 $ \Delta {t_{21}} $ 12 $ \Delta {t_{12}} $ 23 $ \Delta {t_{22}} $ 63 $ \Delta {t_{13}} $ 30 $ \Delta {t_{23}} $ 10 $ \Delta {t_{14}} $ 10 $ \Delta {t_{24}} $ 10 表 5 不同工况下驱动功率统计
Table 5 Powers statistics under different working conditions
${\gamma _3}$ 驱动功率/kW $ {k_3} $ $\lambda / {\text{%}}$ $ {P_{{\text{GT}}.{\text{max}}}} $ ${P'_{ {\text{GT} }{\text{.min} } } }$ 0 981 364 0.2 62.9 (0,0.2] 1335 749 0.2 43.9 (0.2,0.4] 1658 1201 0.4 27.6 (0.4,0.6] 2036 1634 0.6 19.7 (0.6,0.8] 2397 2178 0.8 9.1 (0.8,1.0] 2799 2799 1.0 − -
[1] 蒋卫良,韩东劲. 我国煤矿带式输送机现状与发展趋势[J]. 煤矿机电,2008,29(1):1-6. DOI: 10.3969/j.issn.1001-0874.2008.01.001 JIANG Weiliang,HAN Dongjin. Development situation and tendency of native mining belt conveyor[J]. Colliery Mechanical & Electrical Technology,2008,29(1):1-6. DOI: 10.3969/j.issn.1001-0874.2008.01.001
[2] 郭伟东,李明,亢俊明,等. 基于机器视觉的矿井输煤系统优化节能控制[J]. 工矿自动化,2020,46(10):69-75. GUO Weidong,LI Ming,KANG Junming,et al. Optimal energy saving control of mine coal transportation system based on machine vision[J]. Industry and Mine Automation,2020,46(10):69-75.
[3] 王瑾. 井下胶带输送机自适应控制系统的设计[J]. 工矿自动化,2011,37(4):94-96. WANG Jin. Design of adaptive control system of belt conveyor of coal mine underground[J]. Industry and Mine Automation,2011,37(4):94-96.
[4] 孙伟,王慧,杨海群. 带式输送机变频调速节能控制系统研究[J]. 工矿自动化,2013,39(4):98-101. DOI: 10.7526/j.issn.1671-251X.2013.04.027 SUN Wei,WANG Hui,YANG Haiqun. Research of energy-saving control system with frequency-conversion speed-regulation for belt conveyor[J]. Industry and Mine Automation,2013,39(4):98-101. DOI: 10.7526/j.issn.1671-251X.2013.04.027
[5] 雷汝海,赵强. 矿井带式输送机节能优化与智能控制系统研究[J]. 煤炭技术,2017,36(12):184-186. LEI Ruhai,ZHAO Qiang. Research of energy saving optimization and intelligent control system of mine belt conveyor[J]. Coal Technology,2017,36(12):184-186.
[6] 郝洪涛,杨庭杰,张超. 基于负载估计的带式输送机系统节能控制方法研究[J]. 煤炭科学技术,2021,49(7):139-146. HAO Hongtao,YANG Tingjie,ZHANG Chao. Research on energy saving control method of belt conveyor system based on load estimation[J]. Coal Science and Technology,2021,49(7):139-146.
[7] 刘鸿利. 基于载荷检测的煤矿带式输送机控制系统[J]. 工矿自动化,2018,44(10):81-84. LIU Hongli. Coal mine belt conveyor control system based on load detection[J]. Industry and Mine Automation,2018,44(10):81-84.
[8] 张振文, 宋伟刚. 带式输送机工程设计与应用[M]. 北京: 冶金工业出版社, 2015. ZHANG Zhenwen, SONG Weigang. Engineering design and application of belt conveyor[M]. Beijing: Metallurgical Industry Press, 2015.
[9] 周广林,韩忠惠,张继通. 基于分形维数的大型带式输送机动态特性研究[J]. 煤炭科学技术,2019,47(2):125-130. ZHOU Guanglin,HAN Zhonghui,ZHANG Jitong. Research on dynamic characteristics of large belt conveyor based on fractal dimension[J]. Coal Science and Technology,2019,47(2):125-130.
[10] 张雅俊,乔铁柱. 基于速度控制的多级带式输送机顺序启动方法[J]. 工矿自动化,2017,43(1):52-55. ZHANG Yajun,QIAO Tiezhu. Method of sequence start of multi-level conveyors based on speed control[J]. Industry and Mine Automation,2017,43(1):52-55.
[11] 张治璞. 王家山煤矿大倾角带式输送机的选型设计及安装[J]. 煤矿机电,2013,34(3):50-54. DOI: 10.3969/j.issn.1001-0874.2013.03.015 ZHANG Zhipu. Type selection design and installation of large angle belt conveyor at Wangjiashan Mine[J]. Colliery Mechanical & Electrical Technology,2013,34(3):50-54. DOI: 10.3969/j.issn.1001-0874.2013.03.015
[12] 张乐,王渊. 煤矿主井带式输送机选型设计[J]. 煤矿 机械,2014,35(7):6-8. ZHANG Le,WANG Yuan. Belt conveyor type selection design of main shaft in coal mine[J]. Coal Mine Machinery,2014,35(7):6-8.
[13] 张科利,高赟,陈洋. 陕煤集团柠条塔煤矿主输送系统顺煤流启动研究及应用[J]. 煤炭技术,2016,35(3):229-231. ZHANG Keli,GAO Yun,CHEN Yang. Research and application of direct coal flow start of main belt conveying system in Ningtiaota Coal Mine[J]. Coal Technology,2016,35(3):229-231.
-
期刊类型引用(24)
1. 景玮烨. 基于IBSA-T-S模糊神经网络的煤矿带式输送机智能控制方法. 机械管理开发. 2025(01): 167-169 .  百度学术
百度学术
2. 刘金华. 变频驱动永磁滚筒的应用价值研究. 能源与节能. 2025(02): 301-303 .  百度学术
百度学术
3. 陈凯. 带式输送机输送系统节能控制优化研究. 凿岩机械气动工具. 2025(03): 40-42 .  百度学术
百度学术
4. 朱奇奇,李敬兆,石晴,刘继超,胡迪. 基于MADDPG的散装物料输送多智能体协同控制. 自动化技术与应用. 2024(03): 10-13+34 .  百度学术
百度学术
5. 甄硕磊. 基于煤流量监测的带式输送机节能控制系统研究. 机械管理开发. 2024(02): 245-247 .  百度学术
百度学术
6. 郝国栋. 矿用带式输送机节能优化智能控制系统的设计应用. 西部探矿工程. 2024(03): 163-165 .  百度学术
百度学术
7. 崔静乐. 带式输送机的节能优化与试运行. 机械管理开发. 2024(03): 199-201 .  百度学术
百度学术
8. 李少楠. 带式输送机用不同材质托辊安全性能对比分析. 机械管理开发. 2024(05): 62-64 .  百度学术
百度学术
9. 王德记,马磊,郭伟东. 基于机器视觉的煤矿井下带式输送机节能调速控制系统设计. 煤炭工程. 2024(06): 28-34 .  百度学术
百度学术
10. 苏丹丹. 带式输送机不同输送带对输送能耗影响分析. 山东煤炭科技. 2024(07): 103-107+126 .  百度学术
百度学术
11. 贾海成,张振国,庄启磊,宋建国,汤浩. 基于智能矿山的煤矿带式输送机负载监测技术研究. 现代制造技术与装备. 2024(09): 1-3 .  百度学术
百度学术
12. 李壮琼. 煤矿带式输送机电气节能改造方法探究. 电气技术与经济. 2024(10): 367-369 .  百度学术
百度学术
13. 宋鑫鑫. 矿用刮板输送机变频调速控制方法研究. 能源与节能. 2024(11): 197-199 .  百度学术
百度学术
14. 卫华军. 基于STM32控制器的带式输送机张紧装置研究. 山西焦煤科技. 2024(10): 5-9 .  百度学术
百度学术
15. 武宁. 基于变频调速的煤矿带式输送机节能控制方法研究. 矿业装备. 2024(12): 100-102 .  百度学术
百度学术
16. 张劲松. 煤矿原煤运输带式输送机节能优化技术研究. 机械管理开发. 2023(03): 241-243 .  百度学术
百度学术
17. 李标,程继明. 矿用带式输送机组节能控制方法研究. 煤矿机械. 2023(05): 27-31 .  百度学术
百度学术
18. 赵越. 煤矿带式输送机自动张紧装置的设计与应用研究. 江西煤炭科技. 2023(02): 248-250 .  百度学术
百度学术
19. 严策. 矿井带式输送机节能优化与智能控制系统研究. 中国新技术新产品. 2023(05): 10-12 .  百度学术
百度学术
20. 于林海. 带式输送机能耗优化控制系统设计与应用. 石化技术. 2023(05): 249-250 .  百度学术
百度学术
21. 王宏伟,刘勰,黄向东. 矿用带式输送机模糊调速控制方法研究. 西安科技大学学报. 2023(04): 816-824 .  百度学术
百度学术
22. 杨杰. 煤矿主运输长距离带式输送机托辊安装工艺研究. 煤矿机械. 2023(09): 101-105 .  百度学术
百度学术
23. 程玮,李申岩. 选煤厂智能输煤系统. 工矿自动化. 2023(S2): 36-39 .  本站查看
本站查看
24. 樊志飞. 煤矿带式输送机节能策略研究及试验. 机械管理开发. 2023(12): 190-191+194 .  百度学术
百度学术
其他类型引用(6)



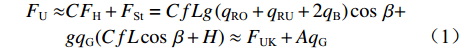
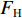
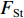
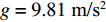
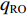
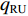
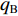
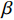
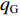
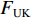
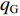
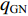
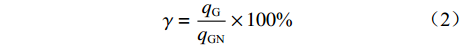
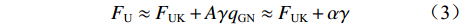
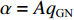
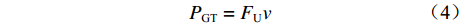
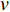
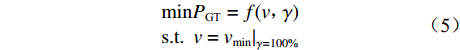
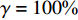
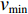
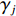
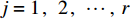
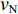
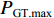
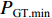
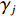
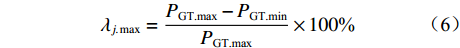
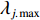
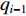
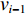
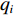
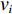
 下载:
下载: