0.   引言

断层结构的复杂性常常导致含断层区域事故频发。因此，对含断层区域进行准确的网格建模，成为分析断层结构的关键。目前四面体自适应网格细化技术多集中于简单层状地质体的三维重构与表达分析，对于结构复杂、数据不连续的含交错断层等复杂地质体进行自适应细化一直是一个难题。因此，如何充分利用四面体自适应网格细化技术对断层处的网格进行更精细化的生成，成为一个亟需解决的问题。

目前，自适应网格细化领域普遍采用基于元素细分（h−细化）方法。该方法通过添加或删除节点来直接构造新的网格，以获得所需的网格分辨率^[1-7]。当该方法所依据的网格模型数据太大时，细化后往往无法提供精确的网格模型，对自适应网格细化的效率和成本产生较大的影响。为提高自适应网格细化效果并降低细化成本，许多学者和工程技术人员在网格划分和细化算法等方面进行了研究。文献[8-9]设计了一种基于最优Delaunay三角剖分的全局细化算法，能根据材质分布控制网格的自适应细化。文献[10]提出一种新的规范求精策略，减少了细化时同一类的数量，提高了细化效率。文献[11]通过二分法求解四维非结构简单网格的局部细化问题，提出了分2个阶段的递归细化过程，保证任意四维非结构网格都能整齐细化。文献[12-13]根据affine变换控制分割顺序对网格进行连续二等分细分，保证了细分的稳定性和一致性。在四面体网格细化方面，文献[14]提出了一种分布式环境下四面体网格的并行适应过程（粗化和细化），使得细化可以更高效执行。文献[15]将网格剖分和动态粒子系统的思想融合在一起，保证质量的同时生成多个体域的、非结构化和自适应四面体网格。文献[16]提出了基于四面体网格的两相流并行自适应网格细化策略，考虑了细分单元的几何特性，以保持细分单元的形状质量。文献[17]提出了一种由网格局部顶点位移驱动的四面体网格变形方法，通过基于RBF的迭代插值对网格进行变形，避免了四面体的反演。文献[18]提出了一种通过对矿体轮廓线进行特征约束，对中间域进行分离或通过距离场对中间域进行拟合的自适应网格剖分方法，生成了无缝、连续的多域网格模型，同时四面体和三角网格质量不受影响。文献[19]提出了基于节点插入与节点移动的网格优化方法，通过细化薄单元提高了整体网格的质量。上述方法虽然通过改进细化策略提高了网格的细化效果，但只适用于简单层状地质体的三维网格细分，用于结构复杂、数据不连续的含交错断层四面体网格细化时，容易出现过度细化，导致断层区域的网格结构受影响。

为了生成更精确的含断层的网格模型，提出一种交错断层四面体自适应网格分级细化方法，通过构建分级细分公式，确定了四面体网格和四面体边的分级；通过对边的升级处理，将细分的8种类型统一为3种类型；使用自适应分级细化生成高质量的网格模型。

1.   交错断层四面体自适应网格分级细化方法

1.1   细化范围自适应确定

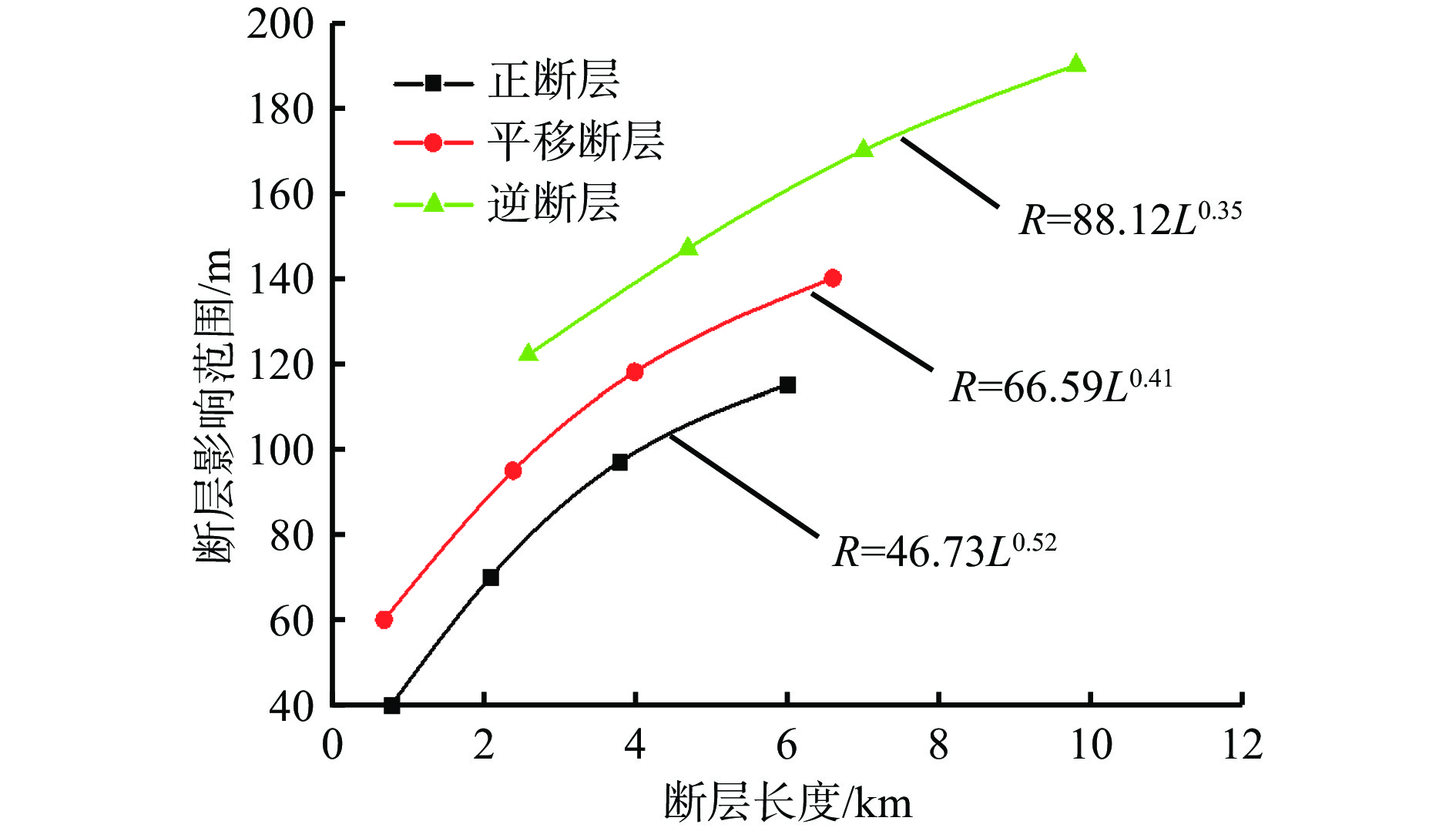
自适应分级细化前，需要先自动确定细化区域的范围，即断层影响范围。在复杂地质体中，断层主要分为正断层、逆断层和平移断层。正断层和逆断层主要呈现上盘宽、下盘窄的不对称发展规律，而平移断层则呈现上下两盘对称分布。在这3种断层类型中，断层影响范围与断层长度的相关性服从幂函数分布。根据断层的类型和长度，断层影响范围计算公式^[20]为

式中：R为断层影响范围；k，b为与区域应力场、断层性质和岩性等有关的拟合常数；L为断层长度。

根据式（1）绘制断层长度与断层影响范围的关系曲线，如图1所示。可看出随着断层长度的增大，断层影响范围增大，但增大幅度逐渐减小。正断层、平移断层、逆断层的影响范围分别在约5，6，7.5 km长度范围内变化明显，之后变化曲线趋于平缓。

图  1  断层长度与断层影响范围关系曲线

Figure  1.  Relationship curves of fault length and fault influence range

下载: 全尺寸图片 幻灯片

1.2   细化范围内的四面体集确定

确定断层的细化范围后，根据四面体中心到断层面网格的最短距离，判断四面体是否在断层的细化范围R内，以确定细化范围内的四面体集。

式中：$ {D_i} $为第i个四面体元素中心点到断层面顶点的最短距离，$ i=1, 2, \cdot\cdot\cdot,N $，N为四面体总数；d为第i个四面体中心点集$ {c_i} $与第g个断层面网格顶点$ {p_g} $的距离，$ g=1,2,\cdot\cdot\cdot,q $，q为断层面网格顶点的总数。

通过式（2），可以得到在细化范围R内的四面体网格集$ T = \{{t_i}\} $，其中$ {t_i} $为第i个四面体网格，四面体中心点集$ C = \{{c_i}\} $，四面体网格顶点集$ V = \{v_i^j\} $，其中$ v_i^j $为第i个四面体网格的第j个顶点，$ j = 1, 2, \cdots , m $，m为四面体网格的顶点总数，四面体边集$ E = \{e_i^r\}$，其中$ e_i^r $为第i个四面体的第r条边，$ r =1 , 2, \cdots , h $，h为四面体边总数。

1.3   四面体网格和边的分级确定

确定细化范围R内的四面体集后，由最短距离$ {D_i} $和细化范围R可计算出四面体网格的分级：

如果$ {D_i} \gt R $，意味着该四面体网格位于断层影响范围之外，不用进一步细化。

由于四面体网格的细化程度由所在边的分级程度决定，而边的分级由所属四面体网格的分级来确定，所以，需确定四面体内边的分级。

式中：$ H_i^r $为第i个四面体的第r条边的分级；$ {G_s} $为第s个含第r条边的四面体网格的分级，$ s = 1, 2, \cdots ,l $，l为含第r条边的四面体网格总数。

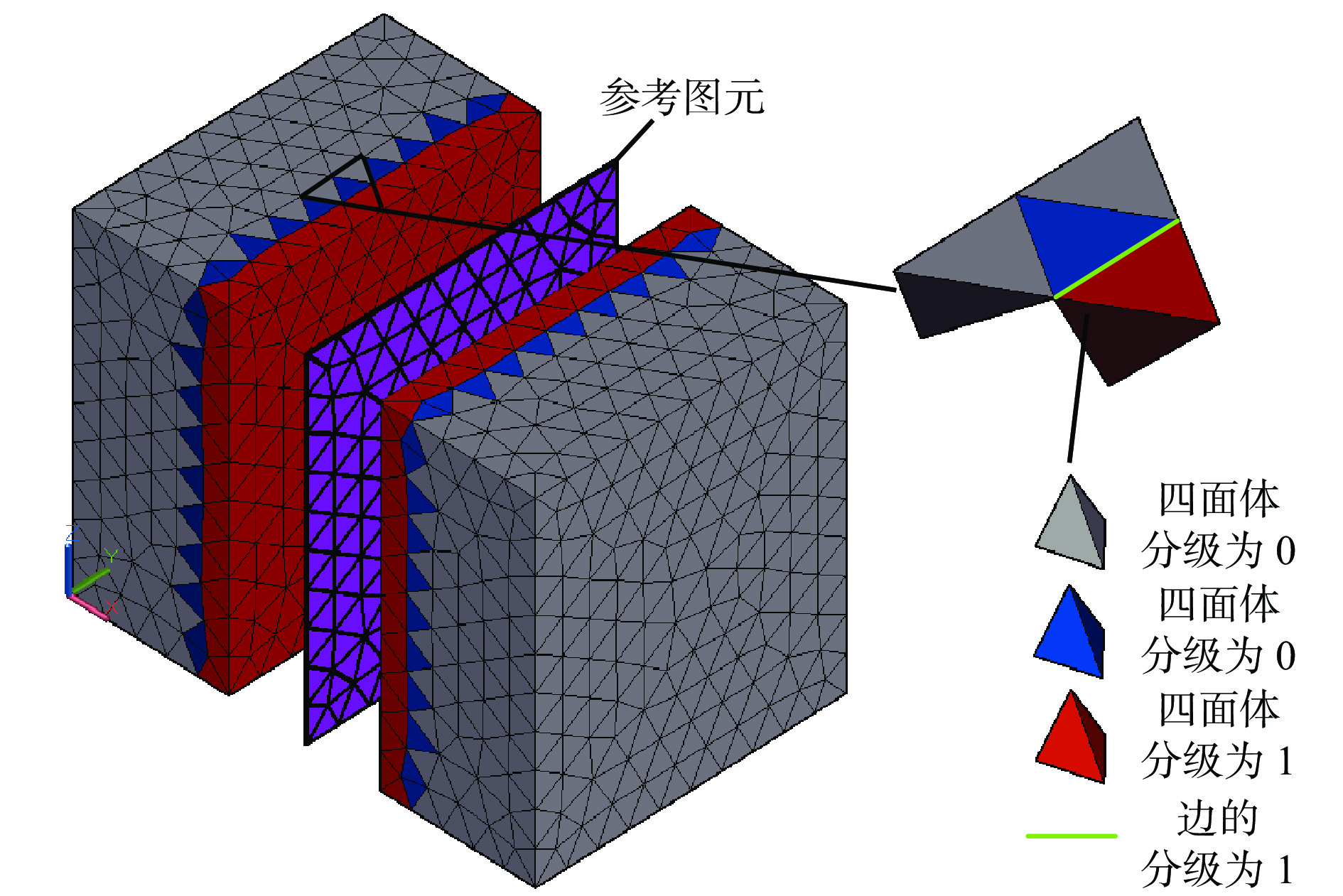
在四面体网格中，蓝色和灰色四面体分级为0，红色四面体分级为1，当蓝色四面体和红色四面体有1条公共边时，则该边的分级等于红色四面体分级，为1，边的分级等于所属四面体中最大的四面体分级，如图2所示。

图  2  确定四面体边的分级

Figure  2.  Grading for determining tetrahedral edges

下载: 全尺寸图片 幻灯片

1.4   四面体自适应网格分级细化

1.4.1   四面体网格分级细化

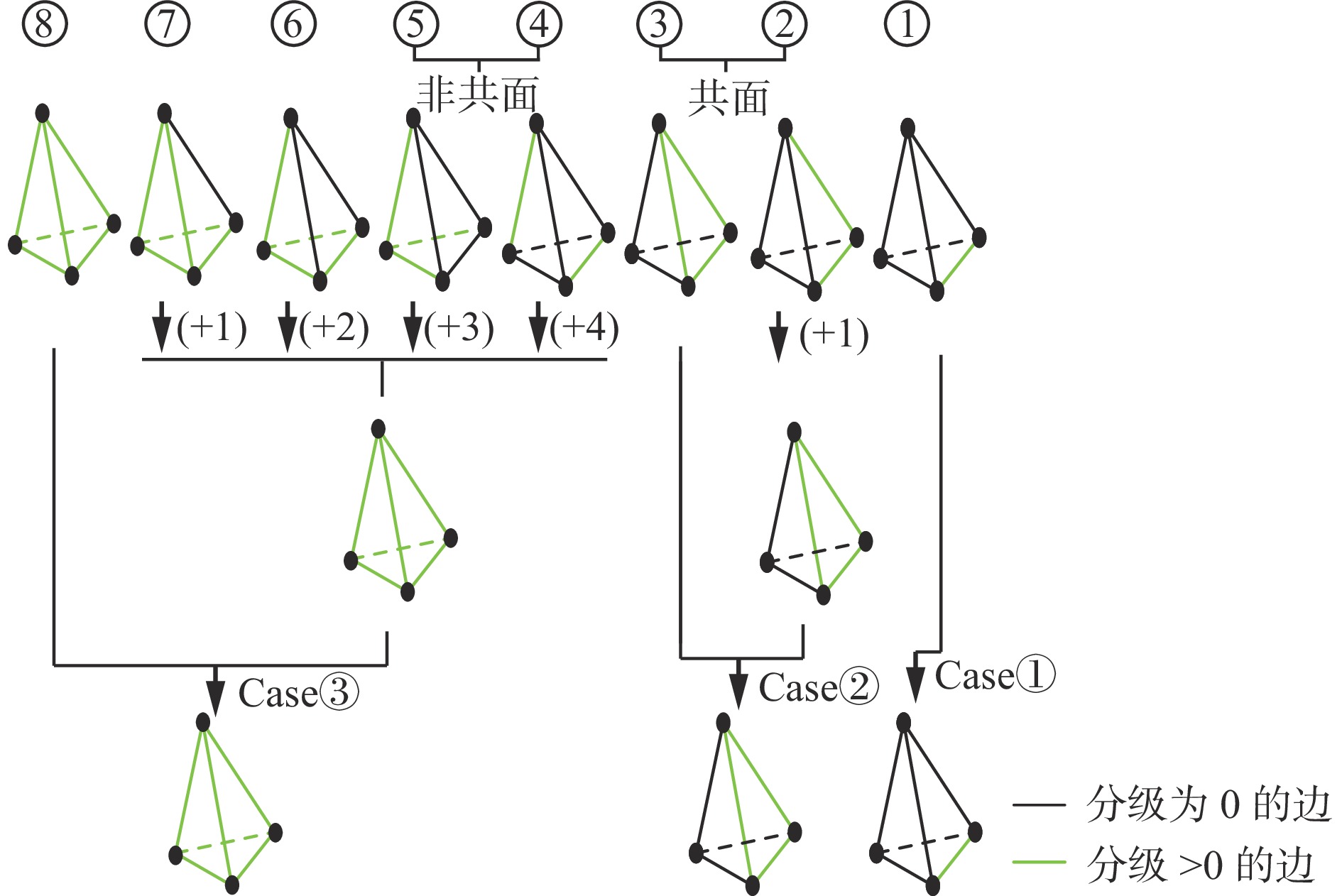
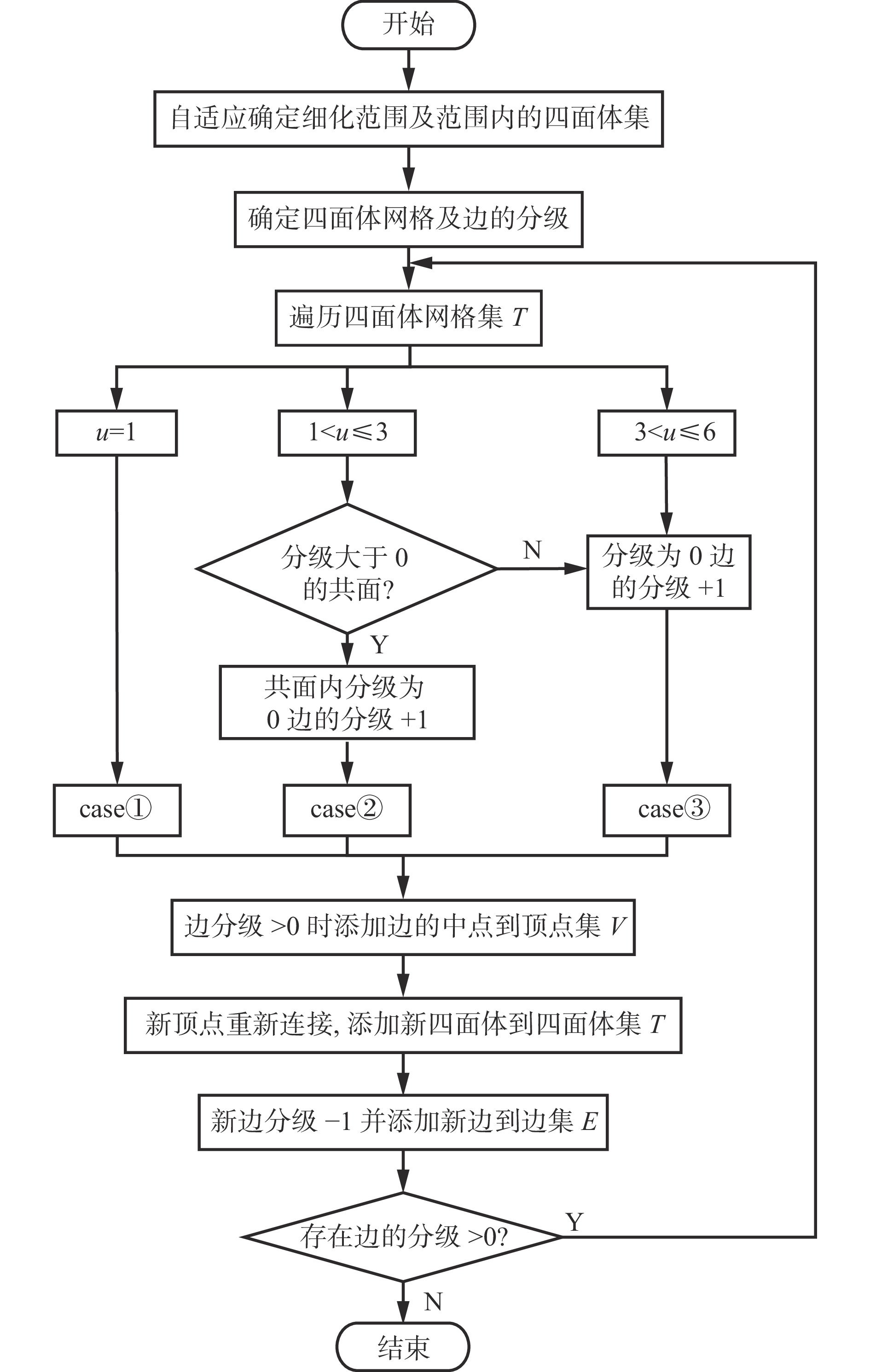
在三维情况下，四面体的网格细分存在2⁶=64种可能的细化类型，虽然可以使用对称性论证来减少类型的数量，但仍然有多种不规则细分类型^[21]。此外，由于在三维情况下四面体网格内边还存在共面问题，所以四面体网格的细化变得更加复杂。在不影响四面体网格细化精度的情况下，为了提高四面体细分算法效率，根据四面体边的分级，对交错断层四面体网格细化分为3种四面体的细分模式，即：1∶2细分（case①）、1∶4细分（case②）和1∶8细分（case③）。

1） 四面体细化分类处理。针对细化范围内的四面体集，用u表示每个四面体边分级大于0的个数。根据u，确定初始四面体网格的8种细分类型^[22]，如图3所示。

图  3  四面体网格边的升级过程

Figure  3.  Upgrade process for tetrahedral mesh edges

下载: 全尺寸图片 幻灯片

当u=1时，该四面体只存在1条边的细分分级大于0，细分类型属于类型①，不需要对边进行升级处理，直接得到case①的网格细分模式。

当$ 1 \lt u \leqslant 3 $时，该四面体分别存在2条和3条边的细分分级大于0，且这些边共处于一个三角形面中，细分类型属于类型②和类型③。对类型②共面内的1条分级为0的边进行升级处理，将该边的分级加1，使类型②升级为3条边的细分分级大于0且3条边共面的情况。对类型③不做升级处理，将这2种类型统一为case②的网格细分模式。

当$ 3 \lt u \leqslant 6 $时，这些四面体存在2条边或2条边以上的细分分级大于0，且这些边存在不共面的情况，细分类型属于类型④−类型⑧。通过对细分分级为0的边进行升级处理，将所有分级为0的边分级都加1，使这些类型统一为case③的网格细分模式。

通过对边的升级处理，四面体网格细化最终统一为3种细分模式，即四面体中有1条边分级大于0（case①）、有3条边分级大于0（case②）和有6条边的分级大于0（case③）。不同四面体类型边的升级情况见表1。

表  1  不同四面体类型边的升级情况

Table  1.  Upgrades for edges of different tetrahedral types

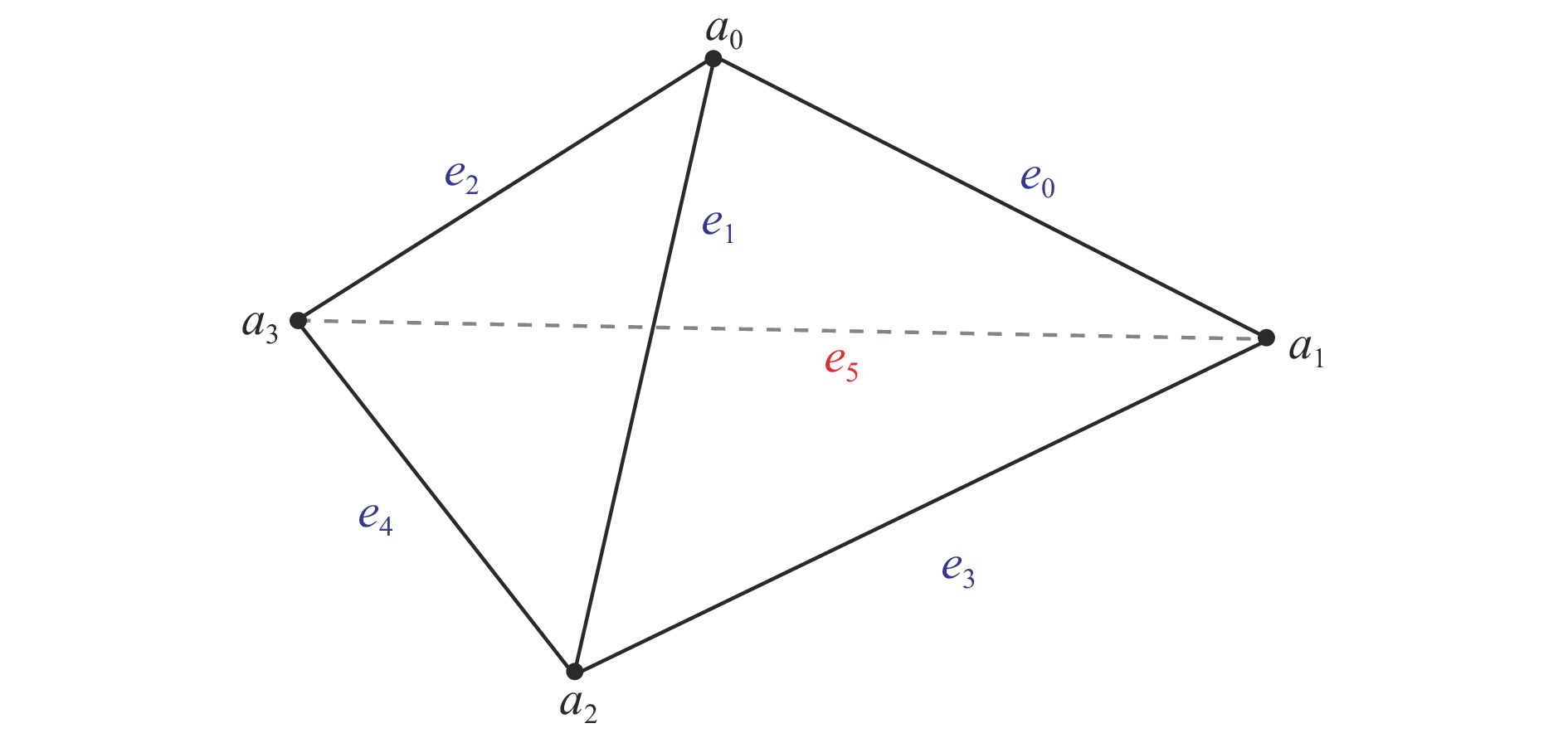
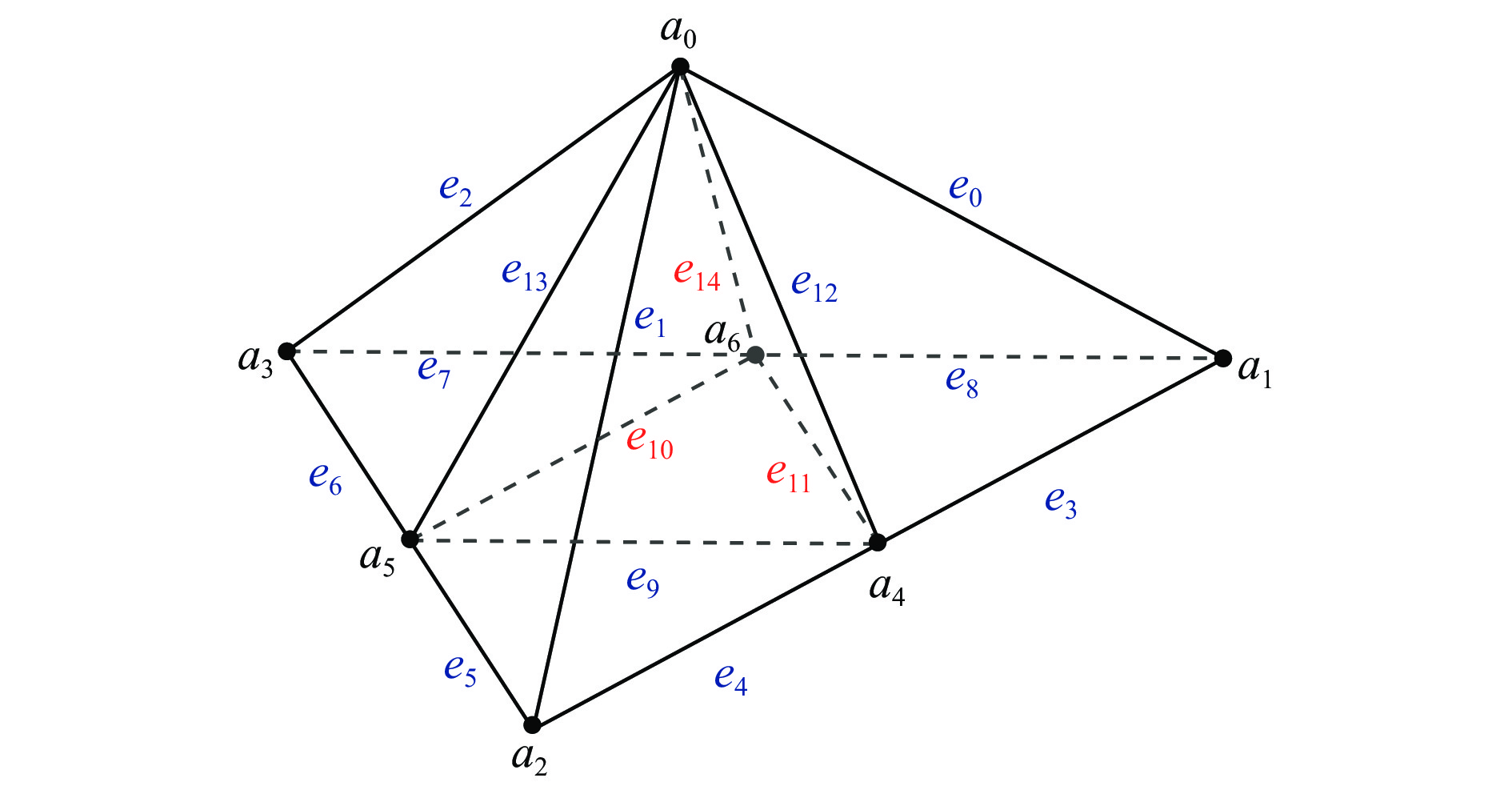
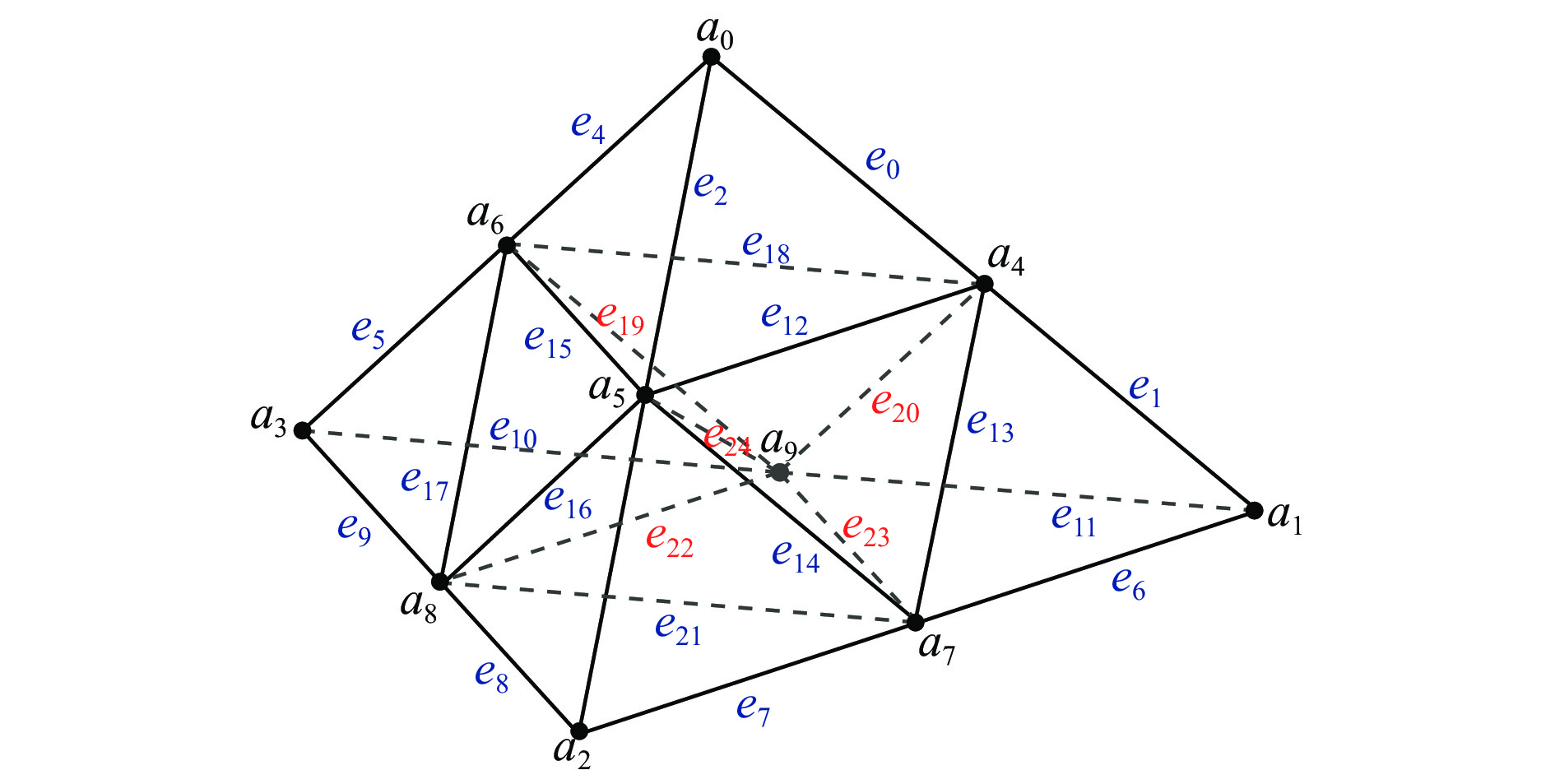
类型	u	分级大于0的 边是否共面	是否改变 边的分级	进行升级的 边个数	分级大于 0的边个数	细分 模式
①	1	是	否	0	1	case①
②	2	是	是	1	3	case②
③	2	否	是	4	6	case③
④	3	是	否	0	3	case②
⑤	3	否	是	3	6	case③
⑥	4	否	是	2	6	case③
⑦	5	否	是	1	6	case③
⑧	6	否	否	0	6	case③

下载: 导出CSV 

| 显示表格

2） 根据细化原则对四面体进行细分。完成四面体集内所有四面体边的升级处理后，根据自适应分级细化的原则，对四面体进行分级细化处理，即将分级大于0的边的中点添加为新的顶点，通过连接新增加的顶点和原顶点，重新组合四面体，原四面体便被划分成多个新的四面体^[23-24]，最终将四面体细分为3种结果，即case①，case②和case③。初始的四面体包含a₀₋a₃ 4个顶点，e₀₋e₅ 6条边，如图4所示。

图  4  初始四面体

Figure  4.  Initial tetrahedron

下载: 全尺寸图片 幻灯片

当有1条边的分级大于0时，四面体的顶点集V中新增1个顶点，顶点变为5个，即a₀₋a₄；通过连接新增加的顶点和原顶点，重新组合四面体，原四面体被细分为2个新四面体，新四面体加入到四面体网格集T中；边被细分为9条，即e₀₋e₈，新生成边的细分分级减1，新边加入到边集E中，细分结果如图5所示。

图  5  case①细分结果

Figure  5.  Subdivision results for case ①

下载: 全尺寸图片 幻灯片

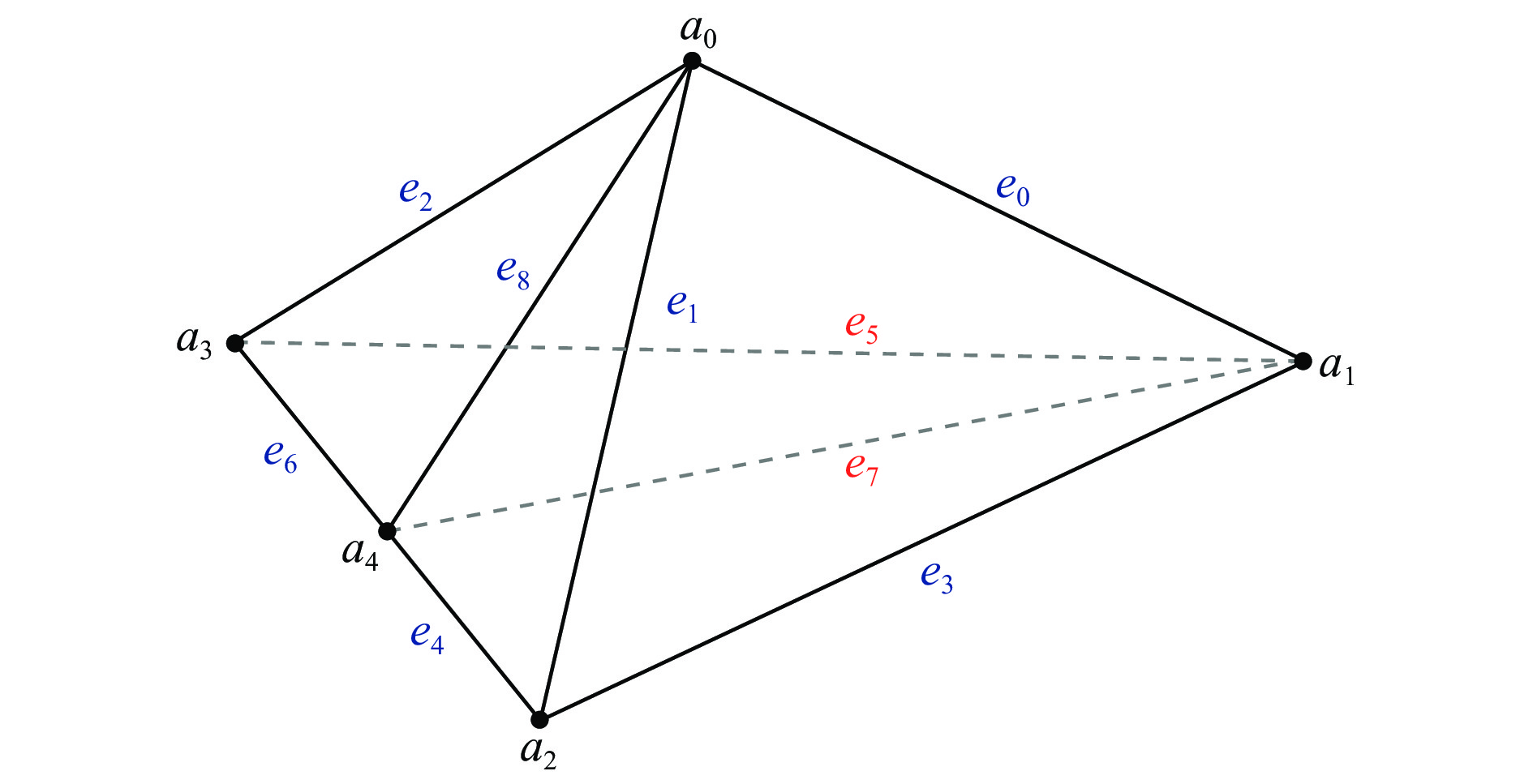
当有3条边的分级大于0时，四面体的顶点集V中新增3个顶点，顶点变为7个，即a₀₋a₆；通过连接新增加的顶点和原顶点，重新组合四面体，原四面体被细分为4个新四面体，新四面体加入到四面体网格集T中；边被细分为15条，即e₀₋e₁₄，新生成边的细分分级减1，新边加入到边集E中，细分结果如图6所示。

图  6  case②细分结果

Figure  6.  Subdivision results forcase ②

下载: 全尺寸图片 幻灯片

当有6条边的分级大于0时，四面体的顶点集V中新增6个点，顶点变为10个，即a₀₋a₉；通过连接新增加的顶点和原顶点，重新组合四面体，原四面体细分为8个新四面体，新四面体加入到四面体网格集T中；边被细分为25条，即e₀₋e₂₄，新生成边的细分分级减1，新边加入到边集E中，细分结果如图7所示。

图  7  case③细分结果

Figure  7.  Subdivision results for case ③

下载: 全尺寸图片 幻灯片

四面体网格自适应分级细化方法流程如图8所示。

图  8  四面体网格自适应分级细化方法流程

Figure  8.  Adaptive grading refinement method for tetrahedral meshes

下载: 全尺寸图片 幻灯片

1.4.2   自适应分级细化示例

以四面体组成的立方体网格模型为例（图9），基于四面体网格自适应分级细化方法，分别以点线面作为细分参考图元，用不同的细化范围对四面体网格进行自适应分级细化，来验证不同细分参考图元和不同细化范围条件下算法的有效性和灵活性^[25-27]。在实验中，模型选取尺寸为200×200×200的四面体网格模型，初始网络模型如图9（a）所示，初始网络模型内部如图9（f）所示。

图  9  自适应分级细化示例

Figure  9.  Example of adaptive grading refinement meshes

下载: 全尺寸图片 幻灯片

1） 以点为细分参考图元。示例以模型顶面3个红色“+”号标记的点作为细分参考图元，细化范围R=50 m。基于四面体网格自适应分级细化方法对点细分，结果如图9（b）所示。模型内部细分结果如图9（g）所示。

2） 以线为细分参考图元。示例以模型侧面红色中线作为细分参考图元，细化范围R=50 m。基于四面体网格自适应分级细化方法对线细分，结果如图9（c）所示。模型内部细分结果如图9（h）所示。

3） 以面为细分参考图元。示例以模型中间红色标记面作为细分参考图元，细化范围R=50 m。基于四面体网格自适应分级细化方法对面细分，结果如图9（d）所示。其为细化后移动两侧网格展示参考图元的结果。模型内部细分结果如图9（i）所示。在以面为细分参考图元的基础上，选取细化范围R=30 m对模型重新进行细化，结果如图9（e）所示。模型内部重新细化结果如图9（j）所示。

在不同细分参考图元和不同细化范围条件下，模型准确细分了细化范围内的四面体网格，证明了四面体自适应分级细化方法可以满足不同的细分参考图元和细化范围，展现出该方法的有效性和灵活性。

2.   自适应分级细化应用

2.1   交错断层四面体网格模型

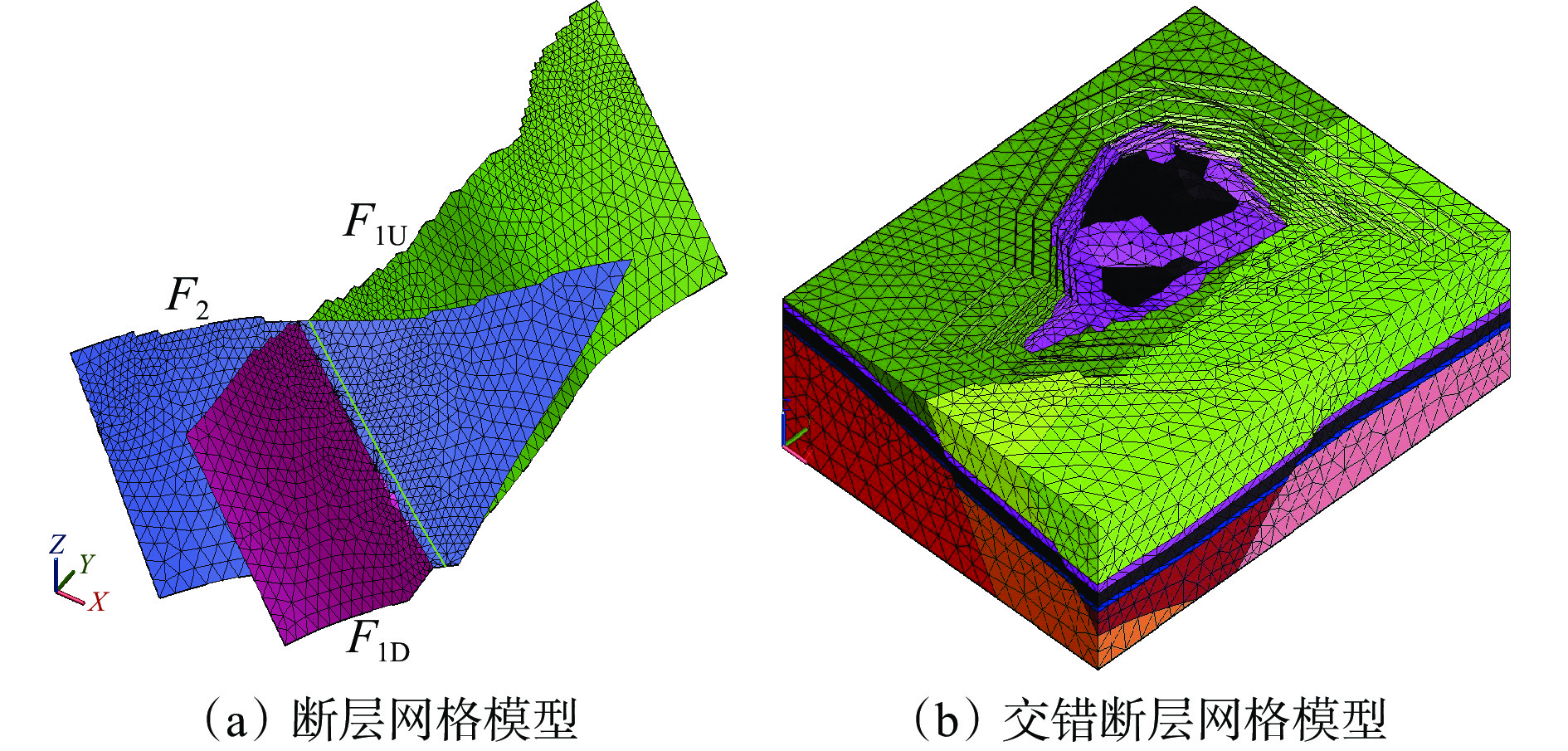
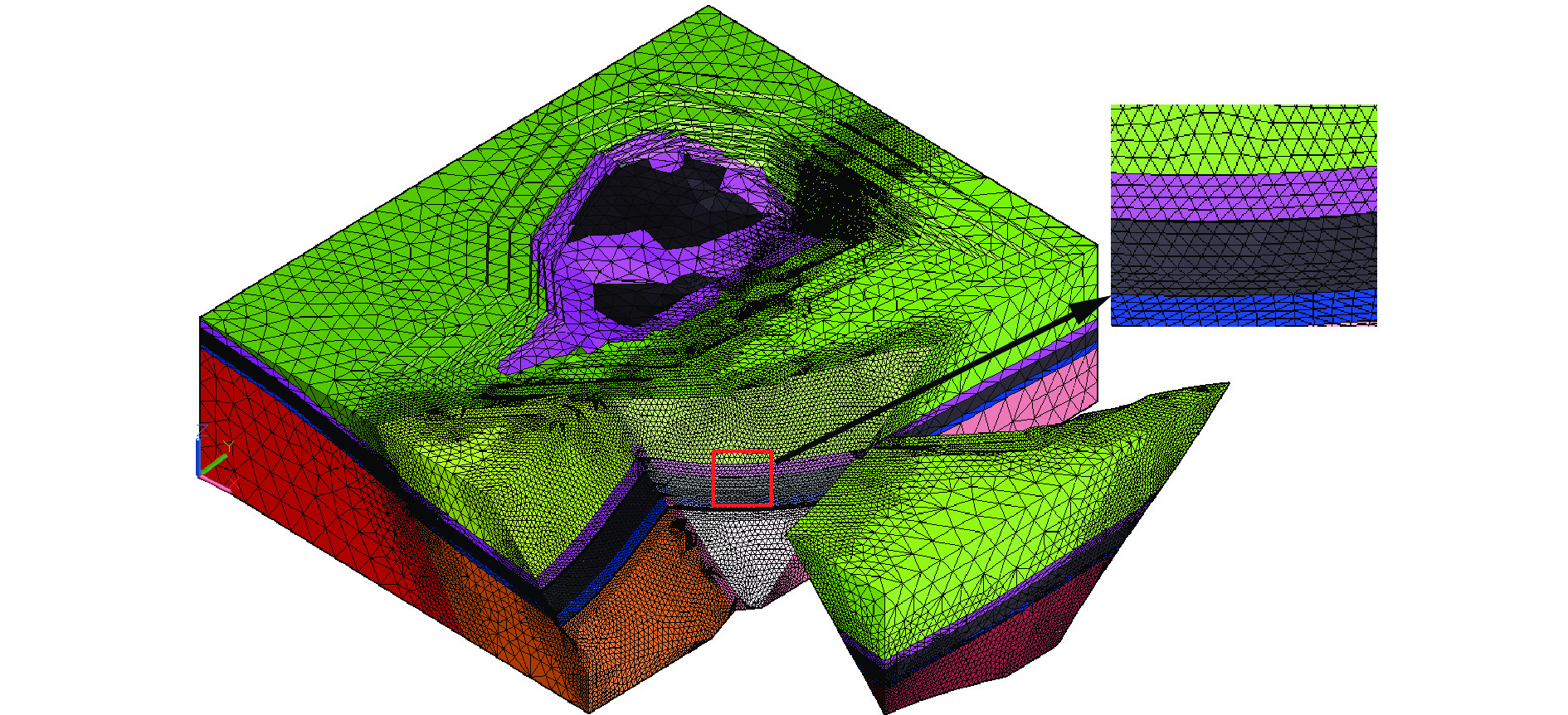
以内蒙古自治区锡林郭勒白音华煤电有限责任公司露天煤矿含交错断层复杂地质体为实例模型，该复杂地质体有F₁和F₂ 2个正断层，长度分别为2.4，1.8 km，矿区断层分布如图10所示。F₁，F₂断层的落差分别为25，30 m。按交错断层生成的时间先后顺序，新生成的断层会将原断层分割成几个部分，F₂晚于F₁生成，F₂将F₁分割成2个部分，分别为F_1U和F_1D，如图11（a）所示。对交错断层封闭的拓扑一致性面域空间模型进行分区域四面体剖分，生成交错断层不规则四面体网格模型^[28-30]。该实体模型共5层，从上到下分别为表土层、第三系、泥岩层、煤层、泥岩层，由于交错断层的影响，将地层分割成20个部分，如图11（b）所示。

图  10  矿区断层分布

Figure  10.  Fault distribution in mining area

下载: 全尺寸图片 幻灯片

图  11  含交错断层四面体网格模型

Figure  11.  Tetrahedral mesh model with intersecting faults

下载: 全尺寸图片 幻灯片

2.2   网格模型细化范围确定

在交错断层网格模型自适应分级细化过程中，通过确定断层影响范围来确定细化区域范围。由图1可知拟合常数k和b分别为46.73和0.52，根据式（1）计算得F₁，F₂断层的细化范围R₁=74 m，R₂=63 m。

2.3   网格模型自适应分级细化

初始的四面体网格模型包含16 570个顶点、69 192个三角面和46 629个四面体，由式（2）得到在细分范围R₁和R₂内的四面体网格集。根据式（3）计算出在R₁和R₂内的四面体网格的分级均为Ⅱ、Ⅰ 2个级别；利用式（4）计算出四面体集内每个四面体网格边的分级；随后在细化范围R₁和R₂内，根据分级，通过新增加顶点和原顶点重新连接四面体，改变网格的单元尺寸，对于含F₂断层的模型，细分用时3.5 s，模型可视化总耗时5.1 s，生成225 620个顶点、935 428个三角面和630 385个四面体，细化结果如图12(a)所示；对于含F₁和F₂断层的模型，细分用时7.3 s，模型可视化总耗时8.9 s，生成457 431个顶点、1 896 517个三角面和1 278 063个四面体，细化结果如图12(b)所示。对于2个断层同时细化的模型，将部分地层移动后，展现出模型内部的细化情况，如图13所示，通过模型内部的细化结果，证明了该方法对模型细化的有效性。

图  12  网格模型自适应分级细化结果

Figure  12.  Adaptive grading refinement results of the mesh model

下载: 全尺寸图片 幻灯片

图  13  网格模型自适应分级细化内部情况

Figure  13.  Internal state of the mesh model's adaptive grading refinement

下载: 全尺寸图片 幻灯片

算法细化时的运行环境为Windows 64位的PC，处理器为Intel（R）Core（TM）i5−10400 CPU，时钟频率为2.90 GHz，具有8 GiB RAM，软件使用AutoCAD 2016。在实例中，不同断层模型算法的计算时间见表2。

表  2  不同断层模型算法的计算时间

Table  2.  Computation time of the different fault model algorithms

断层模型	顶点数	三角面数	四面体数	细分耗时/s	总耗时/s
初始网格模型	16 570	69 192	46 629	0	0
F1断层	225 620	935 428	630 385	3.5	5.1
F1和F 2断层	457 431	1 896 517	1 278 063	7.3	8.9

下载: 导出CSV 

| 显示表格

2.4   网格质量评估及模型数值模拟

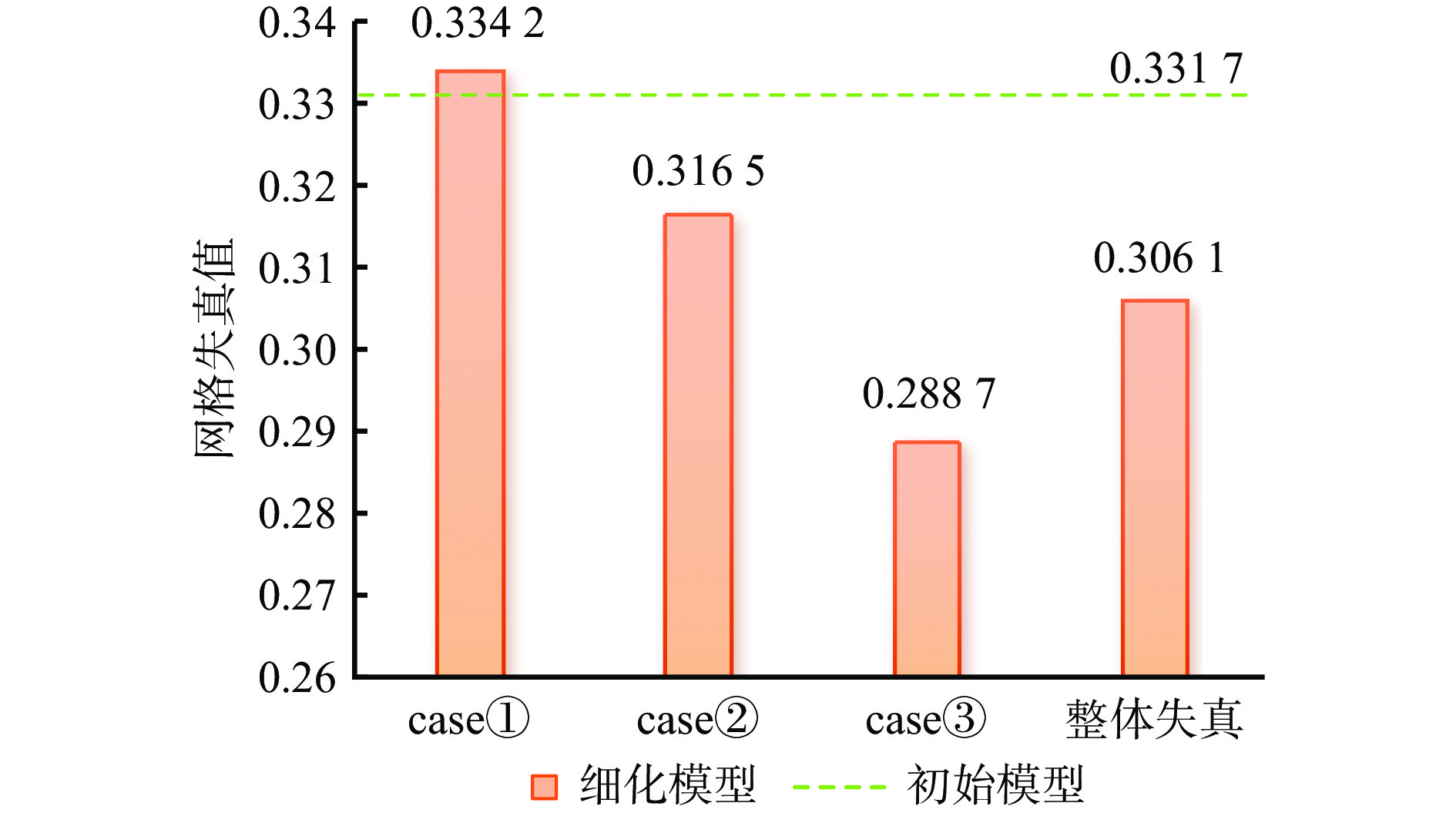
采用基于曲率分析的三维网格质量评估方法对细化前后的网格模型进行质量评估。首先估算各顶点的曲率，然后在每个顶点的邻域内构建一个曲率矩阵，并根据原始网格和失真网格对应曲率矩阵的奇异值差异评估顶点位置的失真，最后通过对这些局部失真进行加权联合，得到网格的整体失真^[31]，结果如图14所示。

图  14  网格整体失真的评估

Figure  14.  Evaluation of overall mesh distortion

下载: 全尺寸图片 幻灯片

从图14可看出，初始网格模型的失真值为0.331 7，虽然case①细分模式细化后的网格失真值略高于初始模型，但该模式细分的网格只占整体细分网格的5.5%，对整体网格模型的失真影响不明显，其他2种细分模型下，网格的失真值都有显著降低，模型的整体失真值从0.331 7降低到0.306 1，证明细化后模型的网格质量得到明显提升。

采用FLAC3D三维数值模拟软件分别对细化前后网格模型进行数值模拟，如图15所示。可看出在相同参数下，未细化模型的最大位移为1.16 m，稳定性系数为1.27，分级细化后模型的最大位移为1.29 m，稳定性系数为1.23。细化后模型的位移云图处于断层处，且能够体现断层分布特征和断层对边坡的影响规律，而未细化模型的位移云图位置偏离断层中心，断层对边坡的影响效果不明显。

图  15  网格模型FLAC3D模拟

Figure  15.  FLAC3D simulations of the mesh model

下载: 全尺寸图片 幻灯片

3.   结论

1） 使用分级细化公式，计算出四面体网格和边的分级；以四面体边的分级为基础，设计了边的升级规则，将细分类型统一为3类，提高了分级细化的效率。

2） 在不同细分参考图元和细化范围上，使用该方法成功优化了四面体网格，展现出该方法的有效性和灵活性。

3） 以内蒙古自治区锡林郭勒白音华煤电有限责任公司露天煤矿含交错断层复杂地质体为实例，采用该方法成功细化了矿区的交错断层网格模型，生成了更精细的网格模型；使用三维网格质量评估算法对细化后的网格模型进行分析，网格的整体失真值从0.331 7降低到0.306 1，表明网格的质量得到提高；通过FLAC3D软件进行模拟实验，结果表明细化后网格模型能更精确地体现断层分布特征和断层对边坡的影响规律。