Research on the application of modulated model predictive control in coal mine power quality management based on STATCOM
-
摘要: 大量电力电子设备及非线性负载接入煤矿电网，使得煤矿电网中存在大量电流谐波及无功功率，严重危害煤矿电网电能质量。传统电能质量治理策略大多采用比例积分（PI）调节器对静止同步补偿器（STATCOM）进行控制，以实现谐波抑制和无功补偿，但其参数难以调节且动态响应慢。针对上述问题，提出了一种基于调制模型预测控制（M2PC）的STATCOM控制策略。首先，采用ip−iq法检测出电网中的谐波电流和无功电流作为M2PC的参考电流；其次，根据参考电流及STATCOM数学模型计算出每个扇区的2个有效矢量和零矢量的占空比及扇区代价函数；然后，通过最小化代价函数得到最佳扇区和该扇区所对应的2个最佳有效矢量和零矢量的占空比；最后，根据空间矢量调制（SVM）方式分配开关脉冲，实现固定的开关频率，从而控制STATCOM发出补偿电流，以抵消电网中的谐波电流与无功电流。仿真和实验结果表明：投入基于M2PC的STATCOM前，电网侧电流畸变严重，电网侧无功功率波动大，电网侧功率因数存在波动且小于1；投入基于M2PC的STATCOM后，由于STATCOM补偿了电网侧谐波电流，使得电网侧电流总谐波畸变率（THD）大幅度降低，且由于STATCOM补偿了负载所需无功功率，电网侧无功功率基本保持为0，电网侧功率因数稳定为1，有效改善了电能质量。Abstract: A large number of power electronic devices and nonlinear loads are connected to the coal mine power grid, causing a large amount of current harmonics and reactive power in the coal mine power grid. It seriously endangers the power quality of the coal mine power grid. The traditional coal mine power quality control strategies mostly use proportional integral (PI) regulators to control static synchronous compensator (STATCOM) to achieve harmonic suppression and reactive power compensation. But their parameters are difficult to adjust and their dynamic response is slow. In order to solve the above problems, a STATCOM control strategy based on modulated model predictive control (M2PC) is proposed. Firstly, the ip-iq method is used to detect the harmonic current and reactive current in the power grid as the reference current for M2PC. Secondly, based on the reference current and STATCOM mathematical model, the duty cycle and sector cost function of the two effective vectors and zero vectors for each sector is calculated. Thirdly, by minimizing the cost function, the optimal sector and the duty cycle of the two optimal effective vectors and zero vectors corresponding to that sector are obtained. Finally, according to the space vector modulation (SVM) method, switching pulses are allocated to achieve a fixed switching frequency. It thereby controls STATCOM to emit compensation current to offset harmonic and reactive currents in the power grid. The simulation and experimental results show that before the adopting of M2PC based STATCOM, the grid side current distortion is severe, the reactive power fluctuation on the grid side is large. The power factor on the grid side fluctuates and is less than 1. After the adopting of M2PC based STATCOM, the total harmonic distortion rate (THD) of the grid side current is significantly reduced due to STATCOM compensating for the harmonic current on the grid side. Moreover, due to STATCOM compensating for the required reactive power of the load, the reactive power on the grid side remains basically 0. The power factor on the grid side remains stable at 1, effectively improving power quality.
-
0. 引言
随着煤矿电网自动化与智能化发展，电力电子设备及各种非线性负载（如大功率晶闸管变流装置、变频调速装置等）在煤矿中的应用越来越多，导致煤矿电网中存在大量电流谐波[1-2]。同时由于各种大功率非线性负载在启动时存在无功冲击，会向电网侧注入大量无功功率，造成煤矿电网中其他设备的安全隐患[3-4]。为尽可能消除电网侧电流谐波和无功功率，需要引入电能质量治理设备，如有源电力滤波器[5]、静止无功补偿器[6]、统一功率/潮流控制器[7]、动态电压恢复器[8]、静止同步补偿器[9-10]（Static Synchronous Compensator，STATCOM）等。其中，STATCOM体积小、动态响应快，能够实时补偿煤矿电网所需要的无功功率，同时可以消除谐波，在煤矿电网中得到广泛应用[11-12]。
目前，关于STATCOM在电能质量治理方面的应用研究已有很多。文献[12]提出了一种单相功率解耦方法，通过单相锁相环（Phase Lock Loop，PLL）实现有功功率和无功功率的解耦，并提出了零序能量转换的有功功率补偿策略，通过零序电流注入的方法，实现在不平衡电网下的功率重新分配，达到三相功率平衡。文献[13]提出了一种无PLL的STATCOM，通过坐标变换，根据坐标系之间的关系，精准计算出电网的频率和相位，提高了STATCOM无功补偿性能。文献[14]分析了电网不平衡对STATCOM的影响，提出了一种新的双闭环控制策略，控制STATCOM发出负序电流，减小了负序电压对STATCOM的影响，抑制了电网电流中3次谐波分量。文献[15]结合储能技术，实现了STATCOM对电压波动、电压越限和三相不平衡的综合治理。然而，以上STATCOM在电能质量治理中的控制方法均采用传统比例积分（Proportional Integral，PI）调节器，但PI调节器参数难以调节且动态响应慢，给STATCOM的实际应用带来困难。
模型预测控制（Model Predictive Control，MPC）具有灵活、简单、动态响应快、可同时控制多个目标等优点[16-17]。其中，有限控制集模型预测控制（Finite Control Set-Model Predictive Control，FCS−MPC）通过在1个采样周期内遍历所有的开关状态以最小化代价函数，最终找到最优开关状态，已在电能质量治理中得到应用[18-20]。然而，由于缺少调制器，导致FCS−MPC控制下的电网电流依然存在较大的纹波，且STATCOM开关频率无法固定。文献[21]提出了一种调制模型预测控制（Modulated Model Predictive Control，M2PC）算法，在MPC的基础上引入调制思想，减小了电流纹波，且具有固定的开关频率。因此，本文将M2PC用于基于STATCOM的煤矿电能质量治理。首先，通过ip−iq法检测出电网侧谐波电流及无功电流并作为M2PC的参考电流；然后，计算STATCOM每个扇区对应的有效矢量和零矢量的占空比，采用最小化代价函数方法选出最佳扇区及其对应的最佳有效矢量和零矢量的占空比；最后，根据空间矢量调制（Space Vector Modulation，SVM）方式分配开关脉冲，控制STATCOM发出补偿电流，以抵消电网中的谐波电流与无功电流。
1. STATCOM基本原理
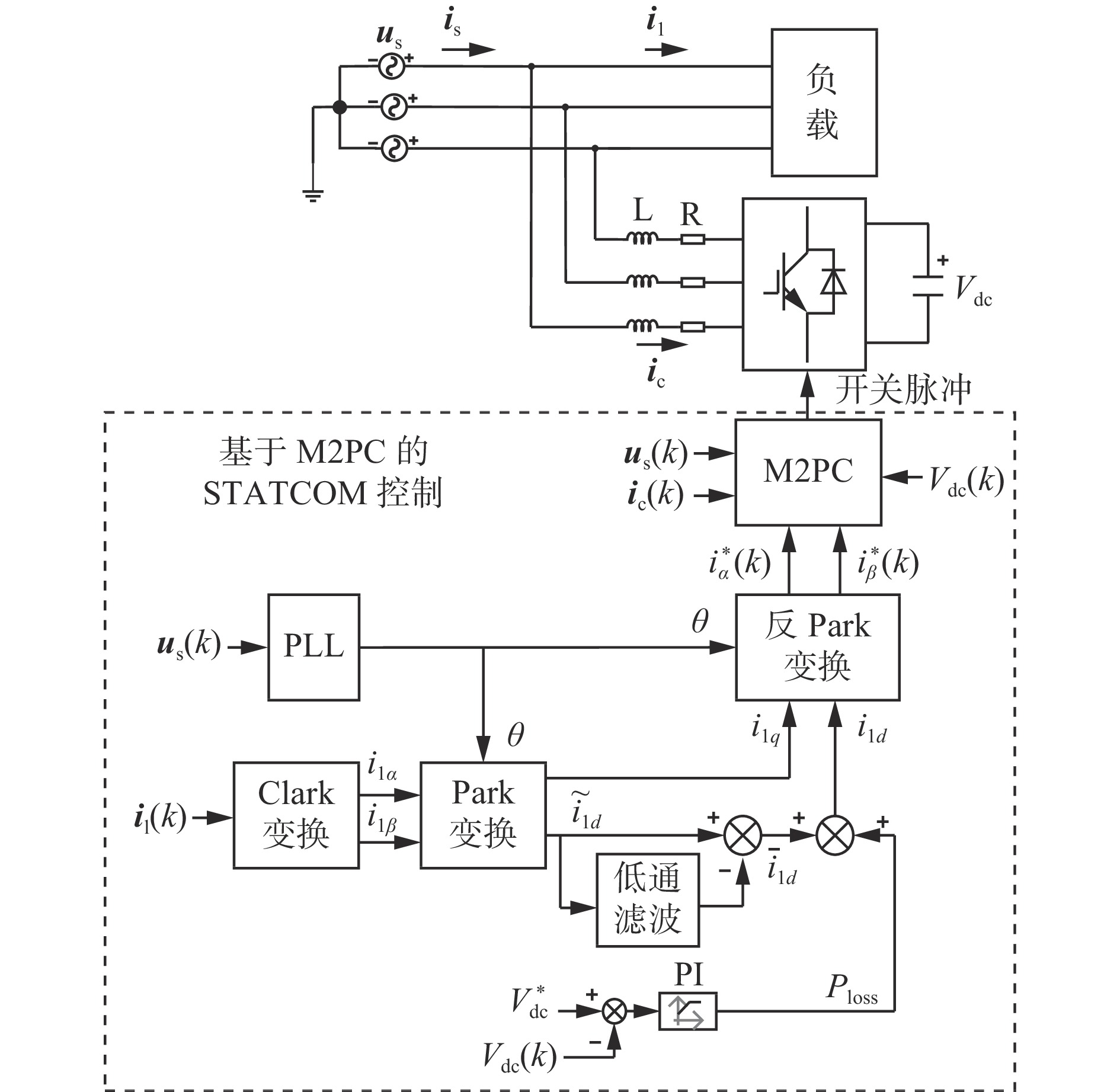
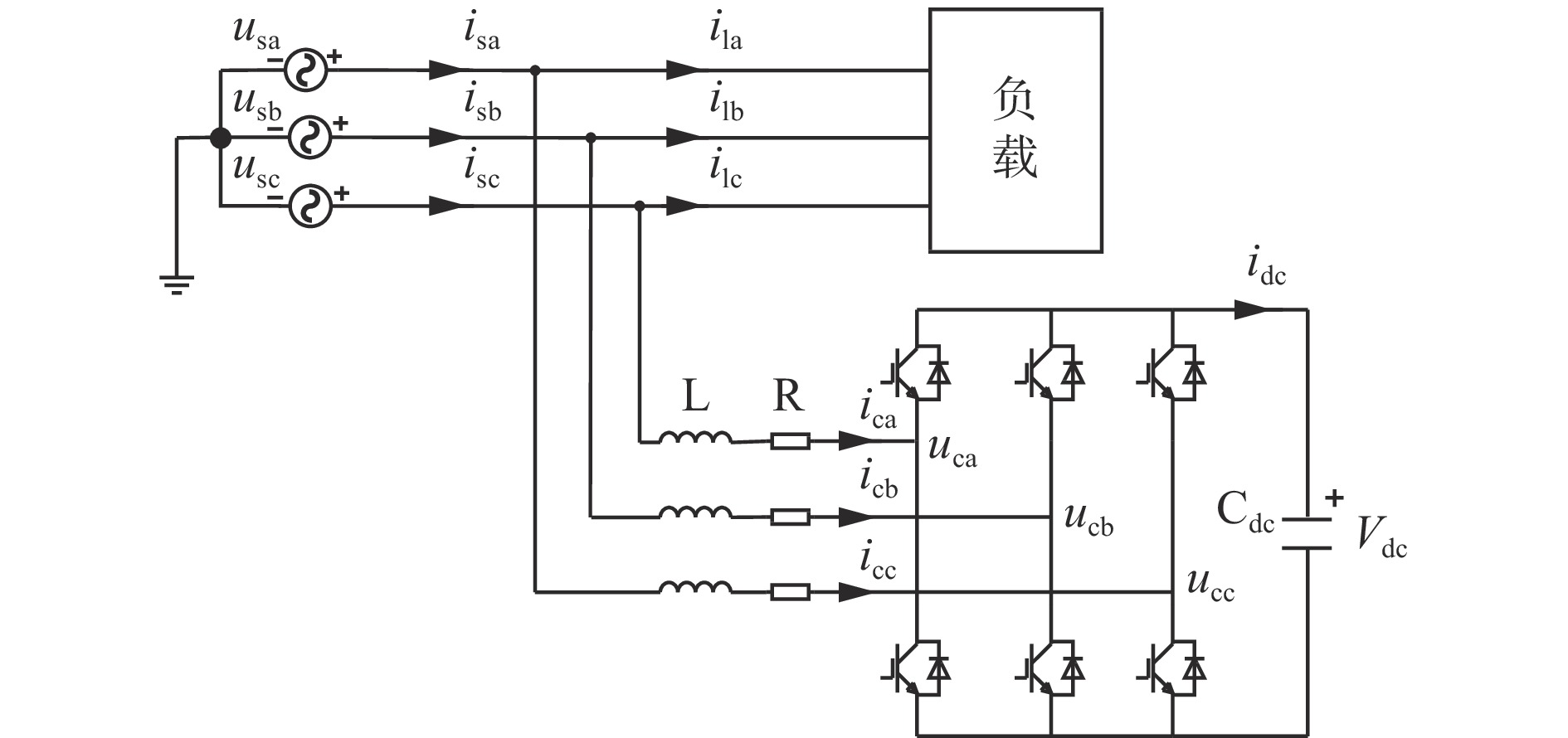
STATCOM通过吸收或发出无功功率来补偿电网中的无功功率，同时能够注入大小相等但方向相反的谐波补偿电流来补偿电流谐波，因此，电网电流变得接近正弦波并与电压相位一致。STATCOM拓扑如图1所示。
由图1可知，电网侧电流由负载电流与STATCOM电流组成：
$$ \left\{ \begin{gathered} {i_{{\text{sa}}}} = {i_{{\text{la}}}} + {i_{{\text{ca}}}} \\ {i_{{\text{sb}}}} = {i_{{\text{lb}}}} + {i_{{\text{cb}}}} \\ {i_{{\text{sc}}}} = {i_{{\text{lc}}}} + {i_{{\text{cc}}}} \\ \end{gathered} \right. $$ (1) 式中：isa，isb，isc为电网侧三相电流；ila，ilb，ilc为负载侧三相电流；ica，icb，icc为STATCOM三相电流。
根据图1和基尔霍夫电压定律，可得STATCOM的连续域数学模型：
$$ \left\{ \begin{gathered} L\frac{{{\text{d}}{i_{{\text{ca}}}}}}{{{\text{d}}t}} = {u_{{\text{ca}}}} - R{i_{{\text{ca}}}} - {u_{{\text{sa}}}} \\ L\frac{{{\text{d}}{i_{{\text{cb}}}}}}{{{\text{d}}t}} = {u_{{\text{cb}}}} - R{i_{{\text{cb}}}} - {u_{{\text{sb}}}} \\ L\frac{{{\text{d}}{i_{{\text{cc}}}}}}{{{\text{d}}t}} = {u_{{\text{cc}}}} - R{i_{{\text{cc}}}} - {u_{{\text{sc}}}} \\ {C_{{\text{dc}}}}\frac{{{\text{d}}{V_{{\text{dc}}}}}}{{{\text{d}}t}} = {i_{{\text{dc}}}} \\ \end{gathered} \right. $$ (2) 式中：L，R分别为STATCOM滤波电感及其阻值；uca，ucb，ucc为输出三相电压；usa，usb，usc为电网侧三相电压；Cdc为直流侧电容；Vdc为直流侧电压；idc为直流侧电流。
$$ \left\{ \begin{gathered} {u_{{\text{ca}}}} = \frac{{{V_{{\text{dc}}}}}}{3}(2{S_{\text{a}}} - {S_{\text{b}}} - {S_{\text{c}}}) \\ {u_{{\text{cb}}}} = \frac{{{V_{{\text{dc}}}}}}{3}(2{S_{\text{b}}} - {S_{\text{a}}} - {S_{\text{c}}}) \\ {u_{{\text{cc}}}} = \frac{{{V_{{\text{dc}}}}}}{3}(2{S_{\text{c}}} - {S_{\text{a}}} - {S_{\text{b}}}) \\ \end{gathered} \right. $$ (3) 式中：Sa，Sb，Sc为三相开关状态，当上桥臂导通、下桥臂关断时为1，当下桥臂导通、上桥臂关断时为0。
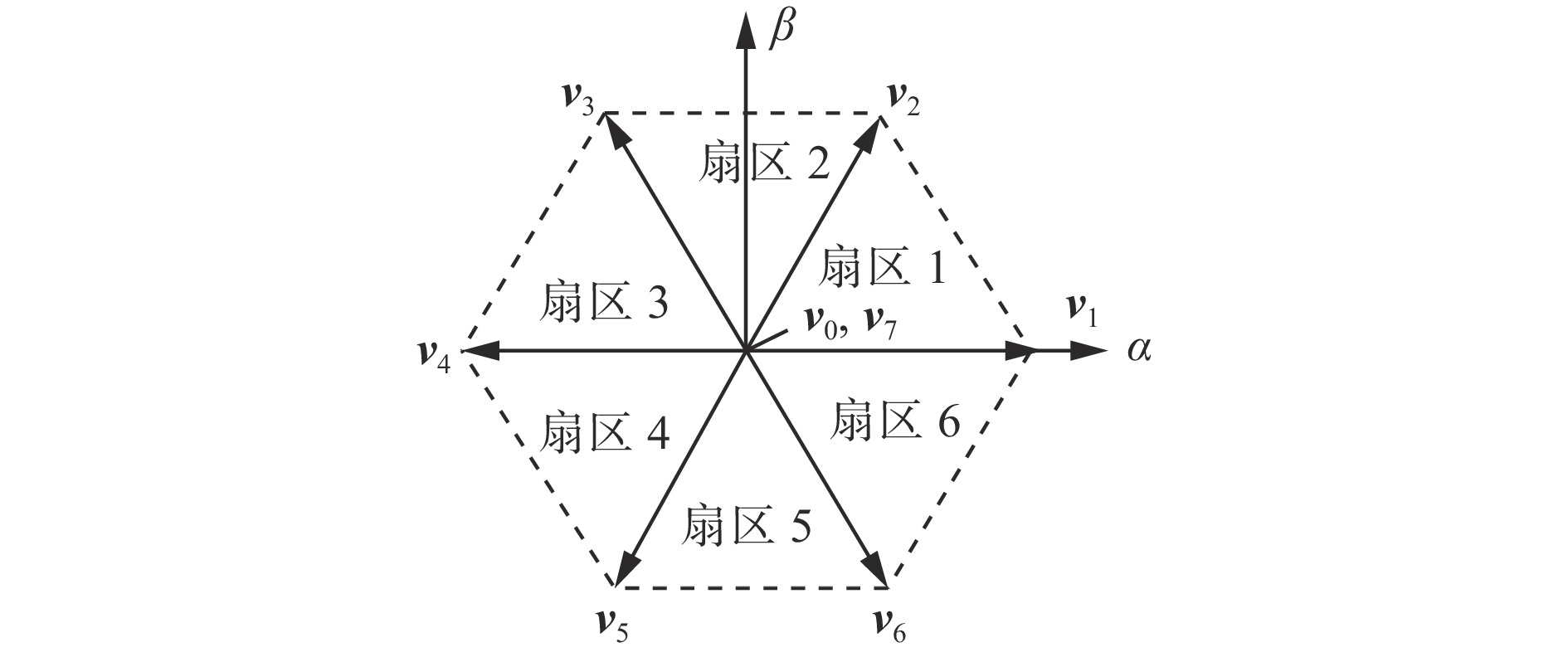
遍历所有开关状态，对于两电平STATCOM，在αβ坐标系下，共有8个开关矢量vy（y $ \in $0，1，…，7）（表1）和6个扇区（图2）。
表 1 STATCOM开关状态及开关矢量Table 1. Switching status and switching vector ofstatic synchronous compensatorSa Sb Sc 开关矢量 0 0 0 v0=0 1 0 0 v1=2Vdc/3 1 1 0 v2=Vdc/3+j$ \sqrt{3} $Vdc/3 0 1 0 v3=−Vdc/3+j$ \sqrt{3} $Vdc/3 0 1 1 v4=−2Vdc/3 0 0 1 v5=−Vdc/3−j$ \sqrt{3} $Vdc/3 1 0 1 v6=Vdc/3−j$ \sqrt{3} $Vdc/3 1 1 1 v7=0 ![]()
图 2 两电平STATCOM扇区及开关矢量分布Figure 2. Sector and switching vector distribution of two-level ofstatic synchronous compensator采用欧拉公式对式（2）进行离散化，并采用Clark变换将离散化数学模型转换到αβ坐标系，可得下一采样时刻（k+1时刻）STATCOM电流预测值的矢量表达式：
$$ {{\boldsymbol{i}}}_{\text{c}}^{\text{p}}(k + 1) = \left(1 - \frac{{R{T_{\text{s}}}}}{L}\right){{{\boldsymbol{i}}}_{\text{c}}}(k) + \frac{{{T_{\text{s}}}}}{L}({{{\boldsymbol{v}}}_y} - {{{\boldsymbol{u}}}_{\text{s}}}(k)) $$ (4) 式中：Ts为采样周期；ic（k）为αβ坐标系下k时刻STATCOM电流矢量；us（k）为αβ坐标系下k时刻电网电压矢量。
2. M2PC基本原理
本文采用M2PC算法控制STATCOM，通过最小化代价函数选取最优矢量，同时加入调制策略。在1个采样周期内，分别选取每一个扇区内相邻2个有效矢量和零矢量以减小输出纹波。根据式（4）可得有效矢量和零矢量作用下k+1时刻的输出电流，从而可得αβ坐标系下3个矢量的代价函数：
$$ \left\{ \begin{gathered} {g_0} = |i_{\alpha }^*(k + 1) - i_{{{ \alpha 0}}}^{\text{p}}| + |i_{\beta }^*(k + 1) - i_{{{\beta 0}}}^{\text{p}}| \\ {g_1} = |i_{\alpha }^*(k + 1) - i_{{{ \alpha 1}}}^{\text{p}}| + |i_{\beta }^*(k + 1) - i_{{{\beta 1}}}^{\text{p}}| \\ {g_2} = |i_{\alpha }^*(k + 1) - i_{{{ \alpha 2}}}^{\text{p}}| + |i_{\beta }^*(k + 1) - i_{{{\beta 2}}}^{\text{p}}| \end{gathered} \right. $$ (5) 式中：g0，g1，g2分别为零矢量、第1个有效矢量、第2个有效矢量对应的代价函数；$ {{i}}_{{ \alpha }}^{\mathrm{*}} $（k+1），$ {{i}}_{ {\beta }}^{\mathrm{*}} $（k+1）为αβ坐标系下k+1时刻STATCOM电流参考值，为了简化，假定电流参考值在1个采样周期内不会发生很大的变化，因此可认为$ {{i}}_{{ \alpha }}^{\mathrm{*}} $（k+1）=$ {{i}}_{{ \alpha }}^{\mathrm{*}} $（k），$ {{i}}_{ {\beta }}^{\mathrm{*}} $（k+1）=$ {{i}}_{ {\beta }}^{\mathrm{*}} $（k）；$i_{{{ \alpha 0}}}^{\text{p}} $，$i_{{ {\beta 0}}}^{\text{p}} $为零矢量作用时αβ坐标系下k+1时刻STATCOM电流；$i_{{{ \alpha 1}}}^{\text{p}} $，$i_{{ {\beta 1}}}^{\text{p}} $为第1个有效矢量作用时αβ坐标系下k+1时刻STATCOM电流；$i_{{{ \alpha 2}}}^{\text{p}} $，$i_{{ {\beta 2}}}^{\text{p}} $为第2个有效矢量作用时αβ坐标系下k+1时刻STATCOM电流。
在每个扇区中都定义1个代价函数：
$$ {g_{{\text{s}}x}} = {d_0}{g_0} + {d_1}{g_1} + {d_2}{g_2}\;\;\; x \in {1,\; 2,\; \cdots,\; 6} $$ (6) 式中d0，d1，d2分别为零矢量、第1个有效矢量、第2个有效矢量的占空比。
矢量的代价函数越小，表示采用该矢量时的控制越精确。为了控制精度的最大化，代价函数越小的矢量所对应的占空比越大。因此规定3个矢量所对应的占空比与其代价函数成反比，且3个矢量之和为1，由此可得
$$ \left\{ \begin{gathered} {d_1}{g_1} = {d_2}{g_2} = {d_0}{g_0} \\ {d_1} + {d_2} + {d_0} = 1 \\ \end{gathered} \right. $$ (7) 求解式（7），得
$$ \left\{ \begin{gathered} {d_1} = {g_0}{g_2}/({g_0}{g_1} + {g_1}{g_2} + {g_0}{g_2}) \\ {d_2} = {g_0}{g_1}/({g_0}{g_1} + {g_1}{g_2} + {g_0}{g_2}) \\ {d_0} = 1 - {d_1} - {d_2} \\ \end{gathered} \right. $$ (8) d0，d1，d2取值范围为[0，1]。若计算出d0，d1，d2大于1，则取值为1；若计算出d0，d1，d2小于0，则取值为0。
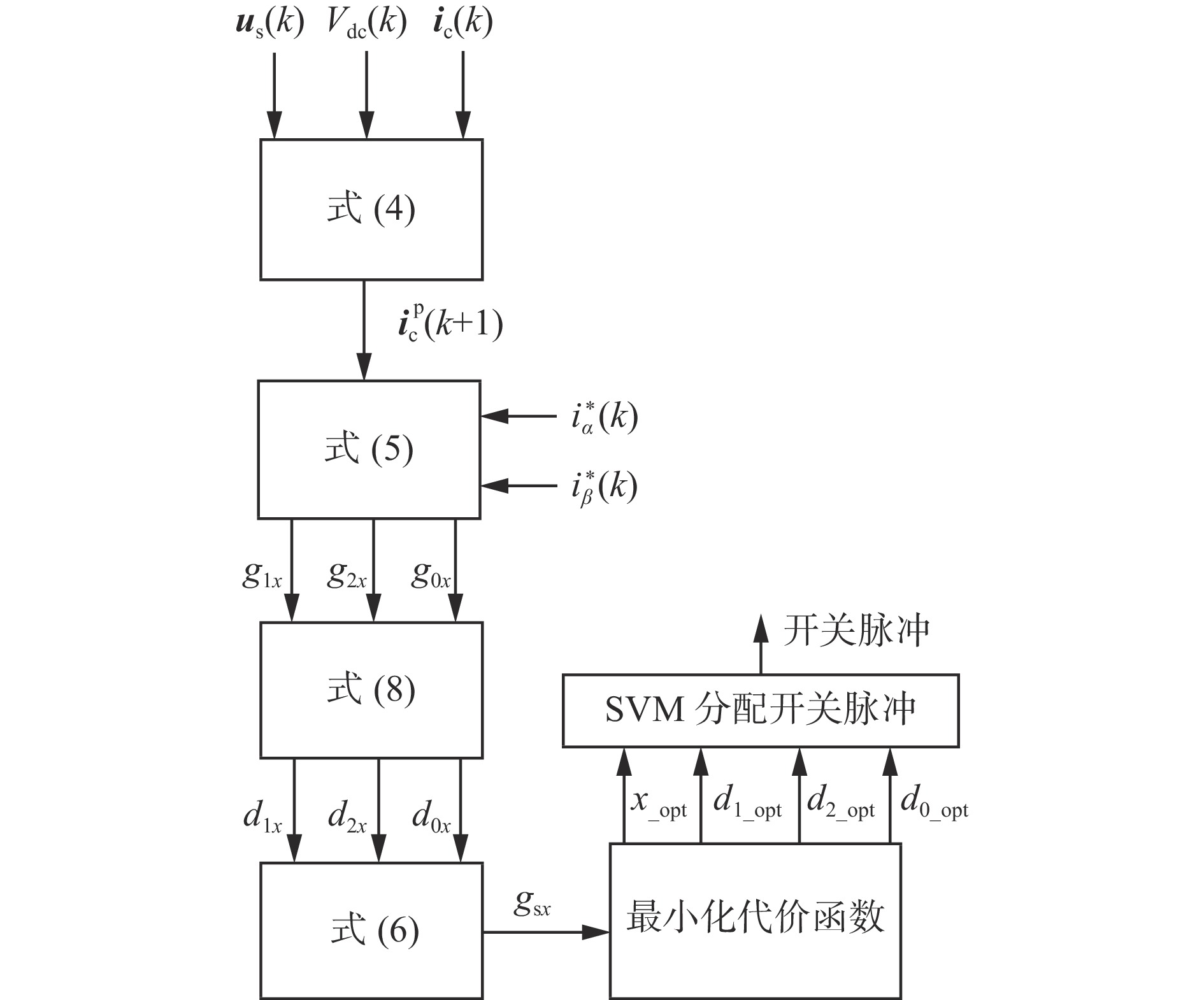
以扇区1为例，第1个有效矢量为v1，第2个有效矢量为v2，零矢量为v0和v7。根据k+1时刻电流参考值$ {{i}}_{\alpha }^{\mathrm{*}} $（k+1）和${{i}}_{\beta }^{\mathrm{*}}$（k+1），通过式（4）和式（5）计算扇区1的2个有效矢量和零矢量的代价函数g11，g21，g01，进而通过式（8）计算3个有效矢量所对应的占空比d11，d21，d01，最后根据式（6）计算出扇区1的代价函数gs1。以此类推，遍历所有的扇区，计算出每个扇区的2个有效矢量和零矢量的代价函数g1x，g2x，g0x，占空比d1x，d2x，d0x和代价函数gsx，找到所有扇区中最小的代价函数，即最小化代价函数，得到最佳扇区x_opt所对应的2个有效矢量和零矢量的占空比d1_opt，d2_opt，d0_opt，再通过SVM方式分配开关脉冲[20]，达到固定开关频率的效果。M2PC控制原理如图3所示。
3. 基于M2PC的STATCOM控制策略
基于M2PC的STATCOM控制原理如图4所示。
![]()
图 4 基于M2PC的STATCOM控制原理Figure 4. Control principle of static synchronous compensator based on modulated model predictive control图4中，is为αβ坐标系下电网侧电流矢量，il为αβ坐标系下负载电流矢量，ic为αβ坐标系下STATCOM电流矢量，us为αβ坐标系下电网电压矢量。通过ip−iq法检测出在dq坐标系下的电网侧谐波电流$ \overline{{i}}_{{{\rm{l}}{{d}}}} $和无功电流ilq：经过PLL对k时刻电网电压矢量us（k）锁相，得到电网角度θ；对k时刻负载电流矢量il（k）采样后进行Clark变换，得到负载电流在αβ坐标系下的分量ilα和ilβ，再进行Park变换，得到负载电流在dq坐标系下的分量$ \tilde{{{i}}}_{{{\rm{l}}d}} $和ilq；用d轴负载电流$ \tilde{{{i}}}_{{{\rm{l}}d}} $减去其低通滤波后的值，得到谐波电流$ \overline{{i}}_{{{\rm{l}}d}} $。为了稳定STATCOM直流侧电压，将电压参考值$V_{{\rm{dc}}}^* $与k时刻直流侧电压实际值Vdc（k）做比较并经过PI调节器得到有功补偿值Ploss，将其加在谐波电流$ \overline{{i}}_{{{\rm{l}}d}} $上，得到有功电流ild。将有功电流ild和无功电流ilq经过反Park变换得到在αβ坐标系下M2PC的电流参考值$ {{i}}_{\alpha }^{\mathrm{*}} $（k）和$ {{i}}_{ \beta }^{\mathrm{*}} $（k）。
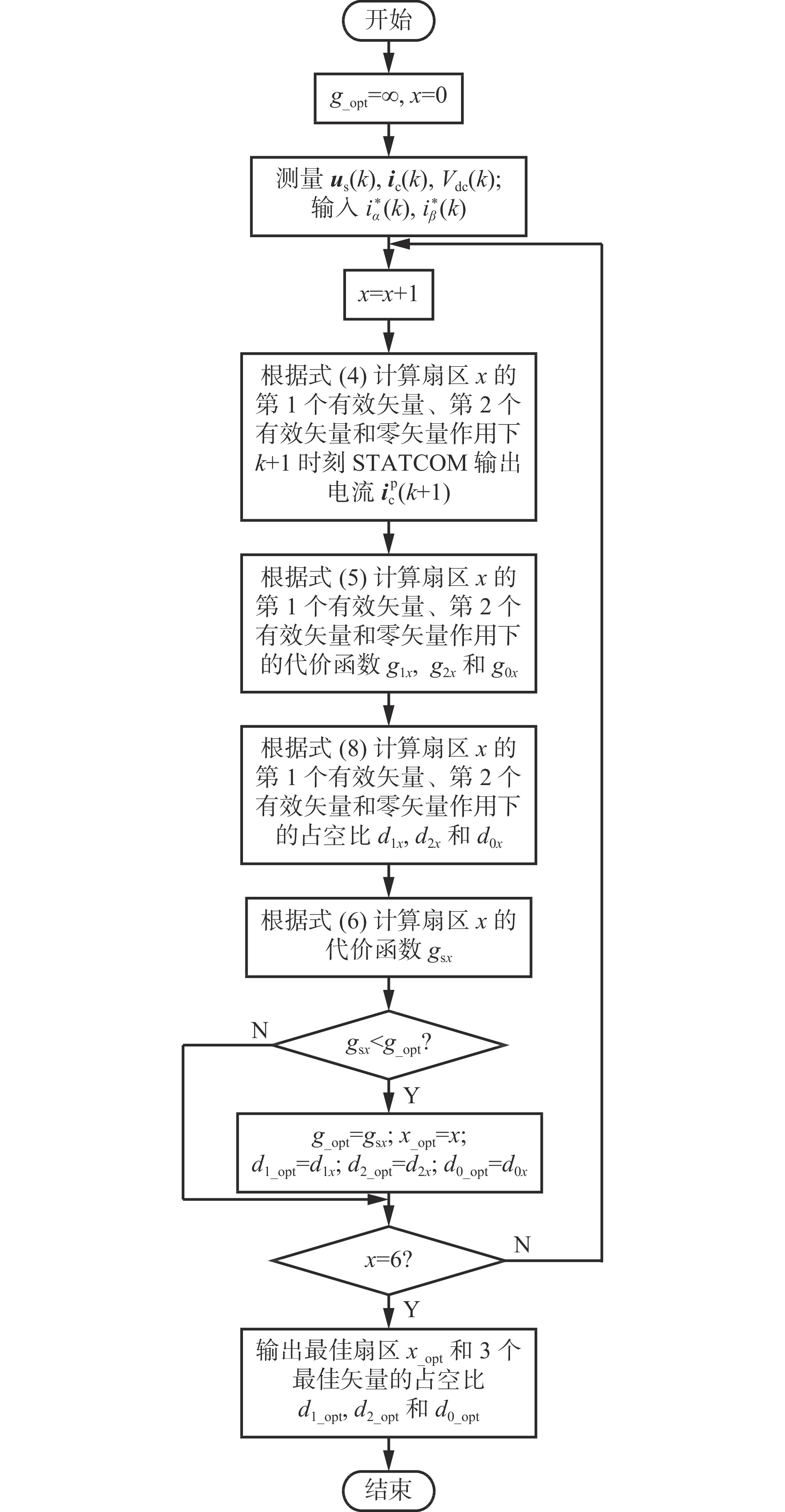
基于M2PC的STATCOM控制流程如图5所示（图中g_opt为遍历6个扇区后代价函数gsx的最小值）。首先，测量k时刻电网三相电压矢量us（k）、STATCOM电流矢量ic（k）和直流侧电压Vdc（k），并输入电流参考值$ {{i}}_{\alpha }^{\mathrm{*}} $（k）和$ {{i}}_{\beta }^{\mathrm{*}} $（k）。然后，根据M2PC基本原理，遍历6个扇区，计算每个扇区的代价函数gsx，以及相邻2个有效矢量及零矢量的占空比d1x，d2x，d0x，通过最小化代价函数得到最佳扇区x_opt和该扇区对应的3个最佳矢量的占空比d1_opt，d2_opt，d0_opt。最后，按照SVM方式分配开关脉冲。
![]()
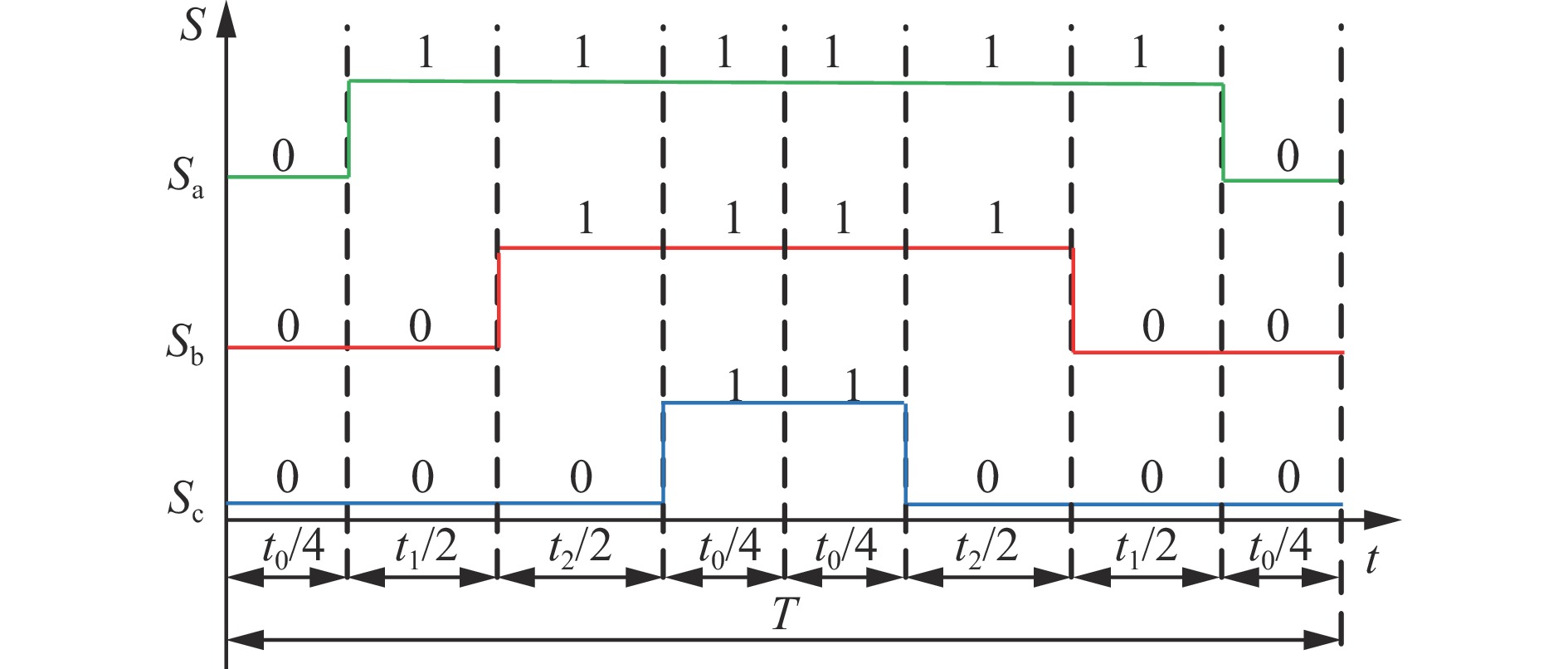
图 5 基于M2PC的STATCOM控制流程Figure 5. Control process of static synchronous compensator based on modulated model predictive control当最优扇区为扇区1（i_opt=1）时，占空比与开关状态S的关系如图6所示。定义在1个开关周期T内，t1为第1个有效矢量作用时间，t2为第2个有效矢量作用时间，t0为零矢量作用时间：
$$ \left\{ \begin{gathered} {t_1} = {d_{1\_{\text{opt}}}}T \\ {t_2} = {d_{2\_{\text{opt}}}}T \\ {t_0} = {d_{0\_{\text{opt}}}}T \\ \end{gathered} \right. $$ (9) ![]()
图 6 M2PC脉冲分配（扇区1）Figure 6. Pulse distribution of modulated model predictive control（sector 1）其他扇区以此类推，按照SVM七段式的脉冲分配方法，即可得到各个扇区的开关状态。在1个开关周期T中，开关器件只会开通或关断1次，因此可以使开关频率固定。
4. 仿真验证
在Matlab/Simulink中搭建两电平STATCOM仿真模型，采用不可控整流二极管作为非线性负载，同时向负载侧注入无功功率。仿真参数见表2。
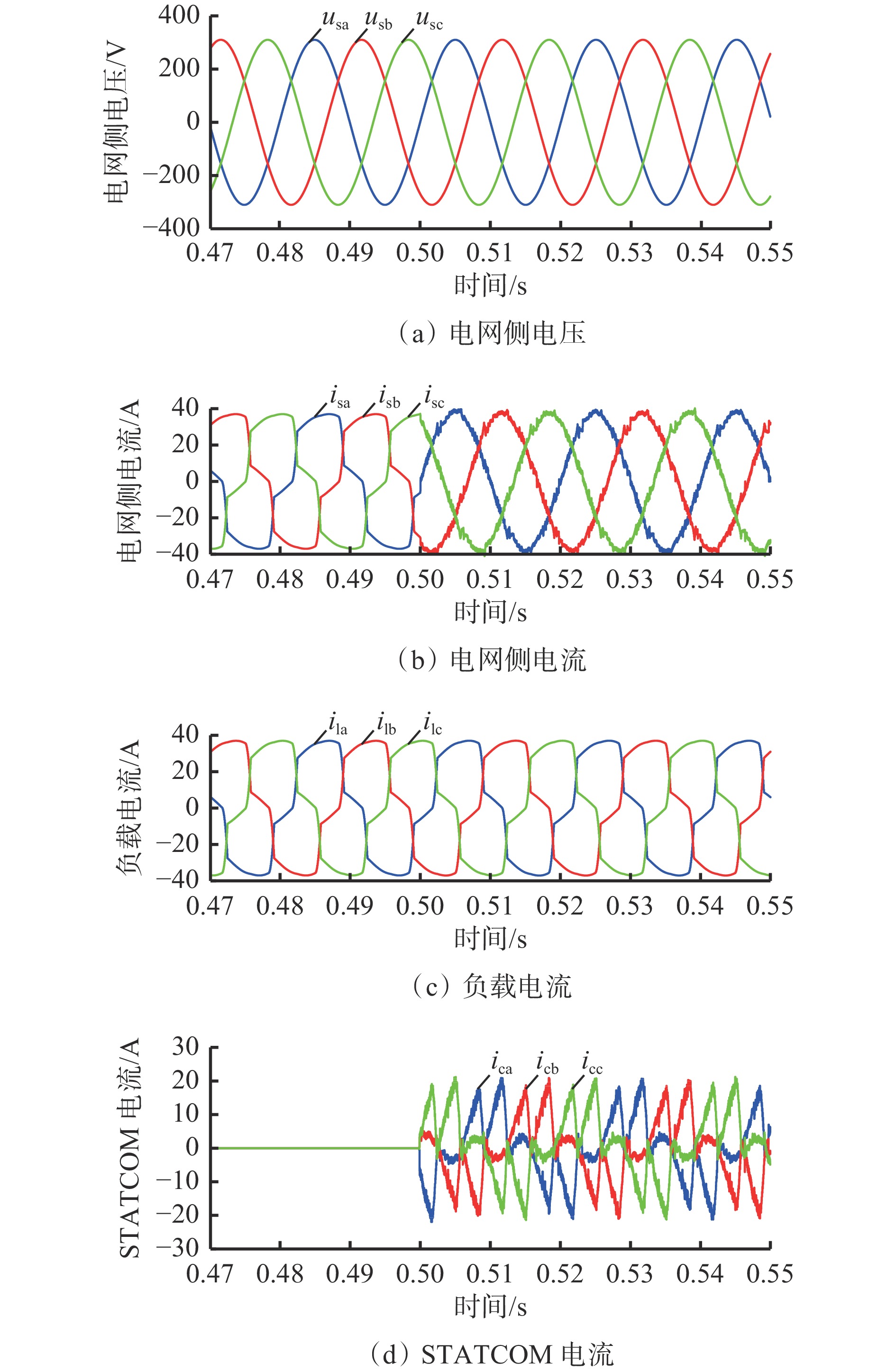
表 2 仿真参数Table 2. Simulation parameters参数 值 电网线电压/V 380 滤波电感/mH 2 滤波电感阻值/Ω 0.1 直流侧电压/V 600 直流侧电容/μF 2 200 采样频率/kHz 20 开关频率/kHz 10 负载侧电阻/Ω 20 在0.5 s投入STATCOM，投入STATCOM前后电压、电流仿真波形如图7所示。可看出在投入STATCOM前，电网侧电流受到负载电流影响，严重畸变，而在投入STATCOM后，由于注入了与谐波电流相反的电流，电网侧电流呈正弦波形；在投入STATCOM前后，电网侧电压和负载电流保持不变。
![]()
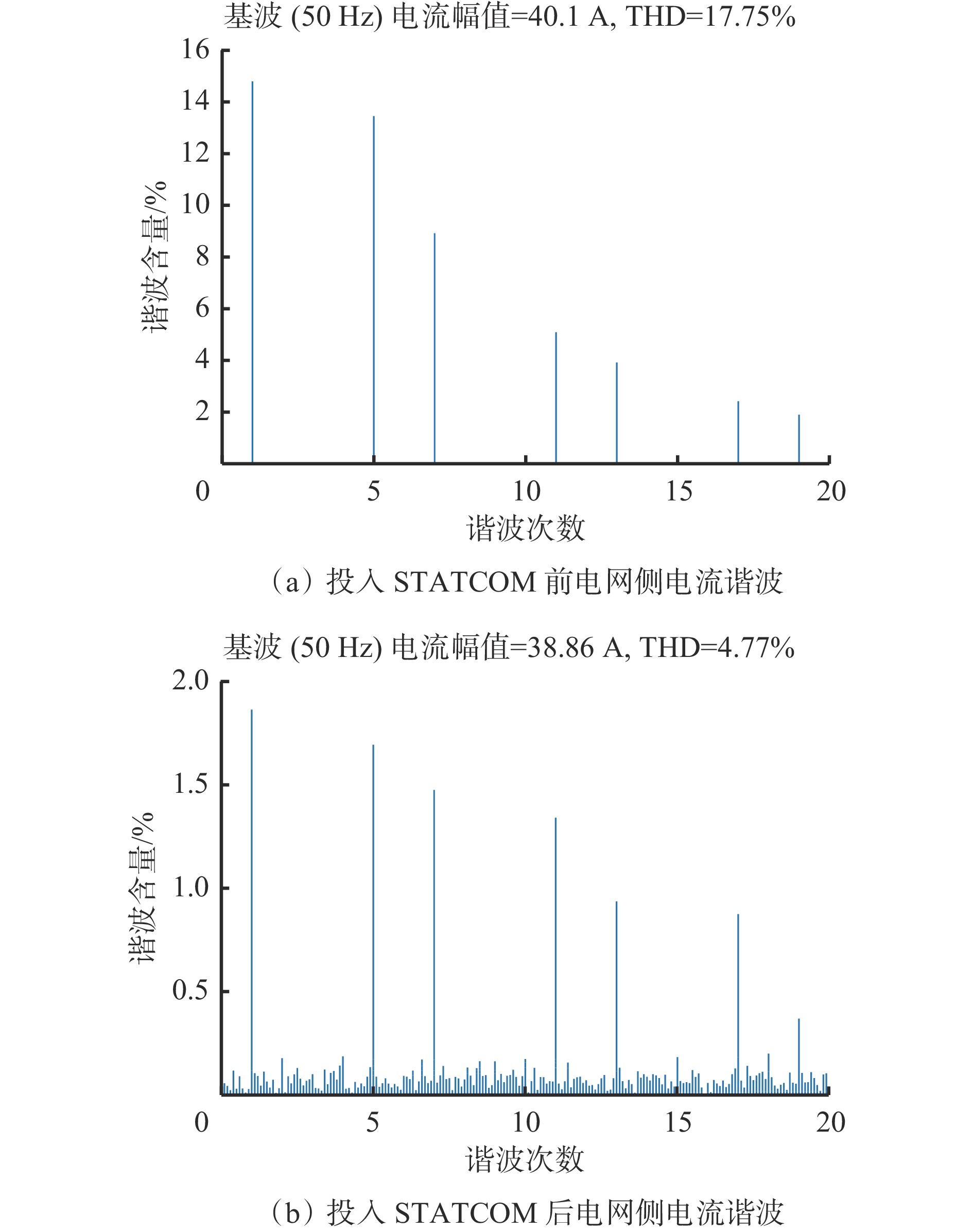
图 7 投入STATCOM前后电压、电流仿真波形Figure 7. Simulation waveforms of voltage and current before and after adopting static synchronous compensator投入STATCOM前后电网侧电流谐波仿真波形如图8所示。可看出在投入STATCOM前，电网侧电流总谐波畸变率（Total Harmonic Distortion，THD）为17.75%，而在投入STATCOM后，电网侧电流THD降至4.77%，极大减小了电网侧电流谐波和THD，改善了电能质量。
![]()
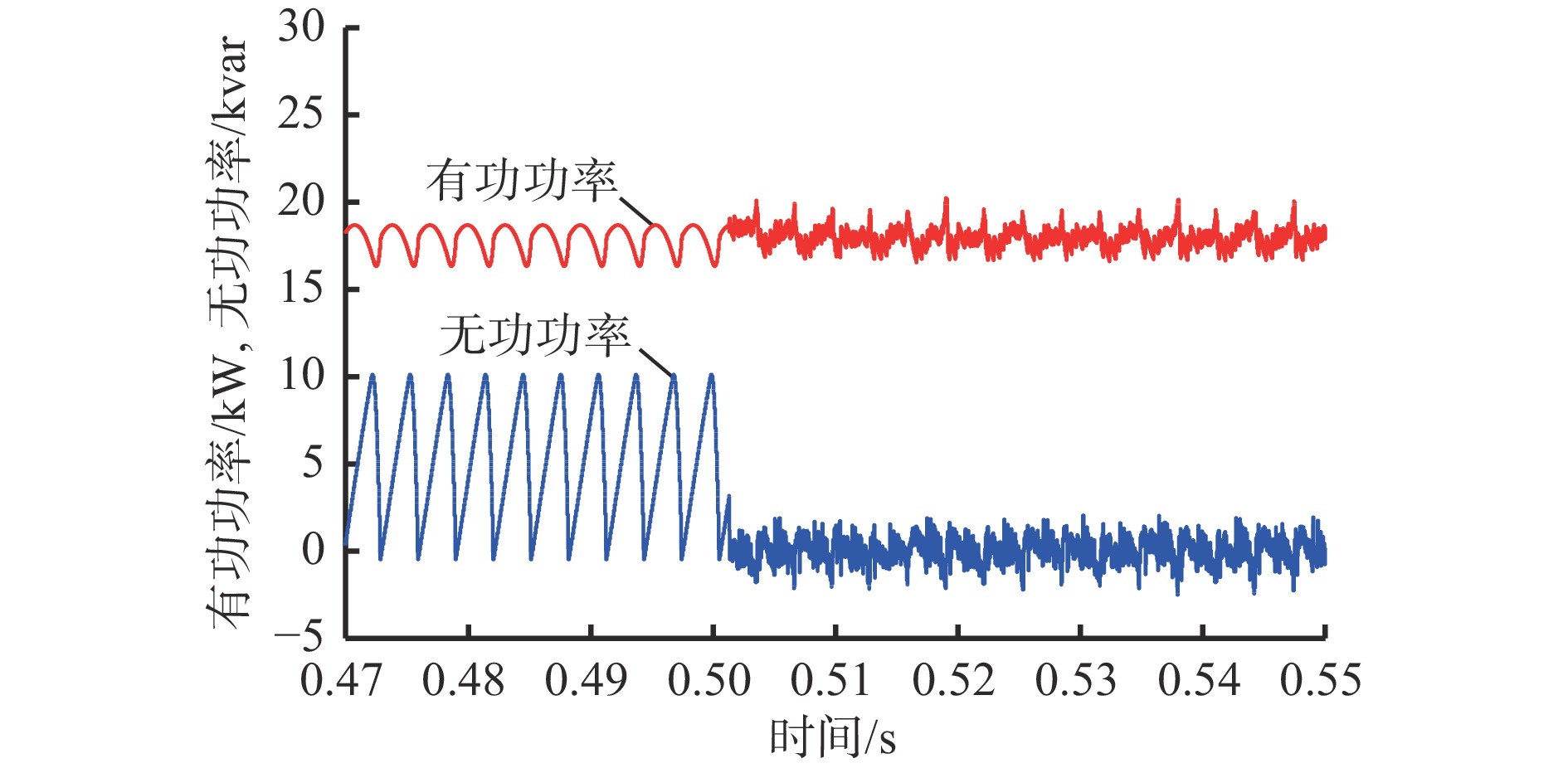
图 8 投入STATCOM前后电网侧电流谐波仿真波形Figure 8. Simulation waveforms of grid side current harmonics before and after adopting static synchronous compensator投入STATCOM前后电网侧有功功率与无功功率仿真波形如图9所示。可看出在投入STATCOM前，电网中存在大量无功功率，在0～10 kvar波动，给电网带来巨大隐患；在投入STATCOM后，电网侧无功功率经过了STATCOM补偿，瞬间维持在0左右，同时有功功率基本保持不变，且从不断波动状态变得更加稳定。
![]()
图 9 投入STATCOM前后电网侧有功功率和无功功率仿真波形Figure 9. Simulation waveforms of grid side active and reactive power before and after adopting static synchronous compensator投入STATCOM后直流侧电压仿真波形如图10所示。可看出直流侧电压在参考值上下轻微波动，基本稳定在参考值附近。
![]()
图 10 投入STATCOM后直流侧电压仿真波形Figure 10. Simulation waveforms of DC-side voltage after adopting static synchronous compensator5. 实验验证
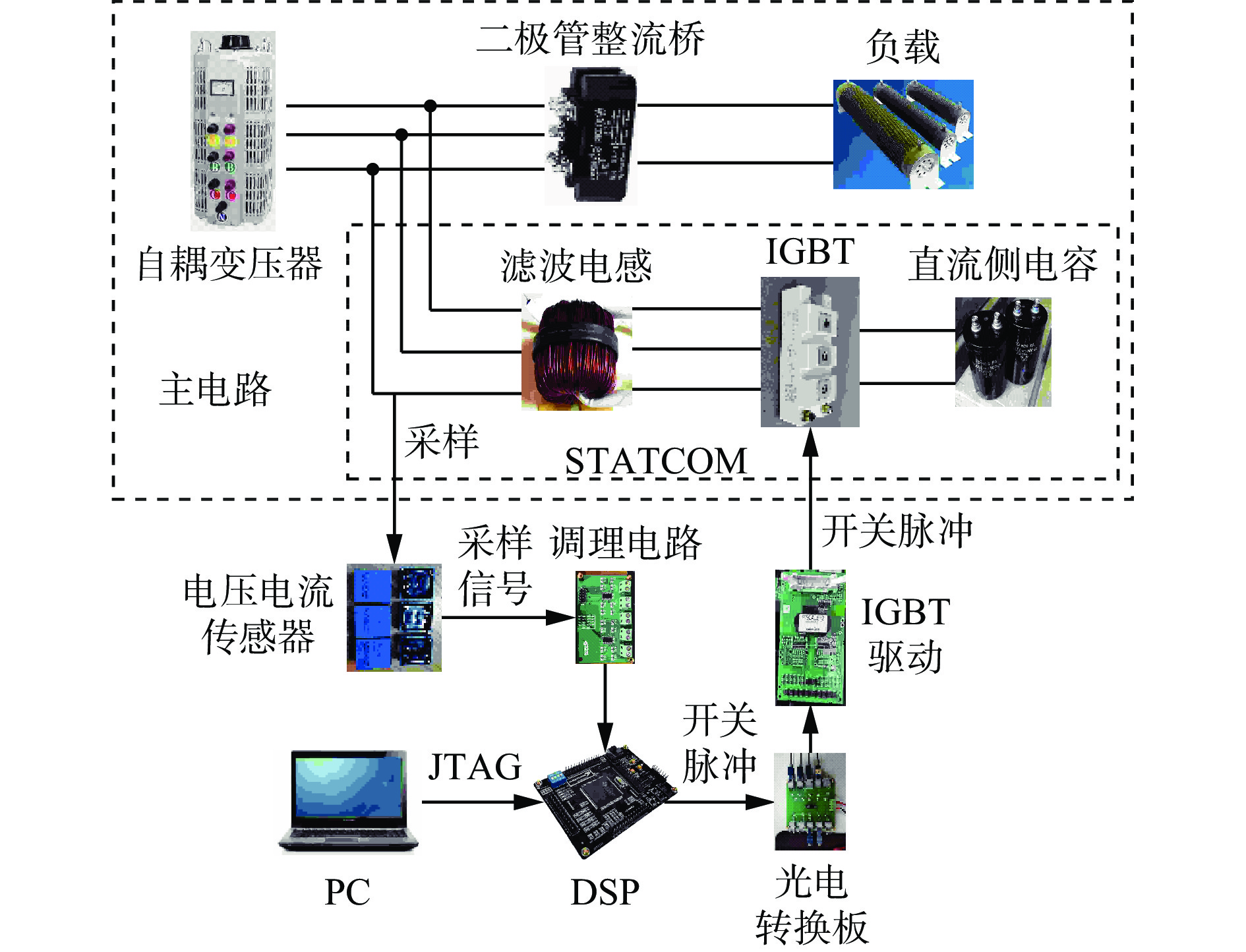
实验平台采用自耦变压器作为三相交流电源，不可控整流二极管作为非线性负载并向电网中注入谐波与无功功率。STATCOM的功率开关器件采用IGBT BSM50GB120DLC，控制器采用DSP TMS320F28335，电压、电流采样模块分别为LV25−P和LA25−NP传感器。实验平台原理如图11所示，电压、电流传感器采集主电路中的电压、电流信号，经过调理电路对信号进行处理后输入DSP中。DSP运行基于M2PC的STATCOM控制策略，生成开关脉冲信号，经过光电转换板将电信号转换为光信号传入IGBT驱动中，最终以开关脉冲的方式驱动IGBT，控制STATCOM正常运行。实验参数见表3。
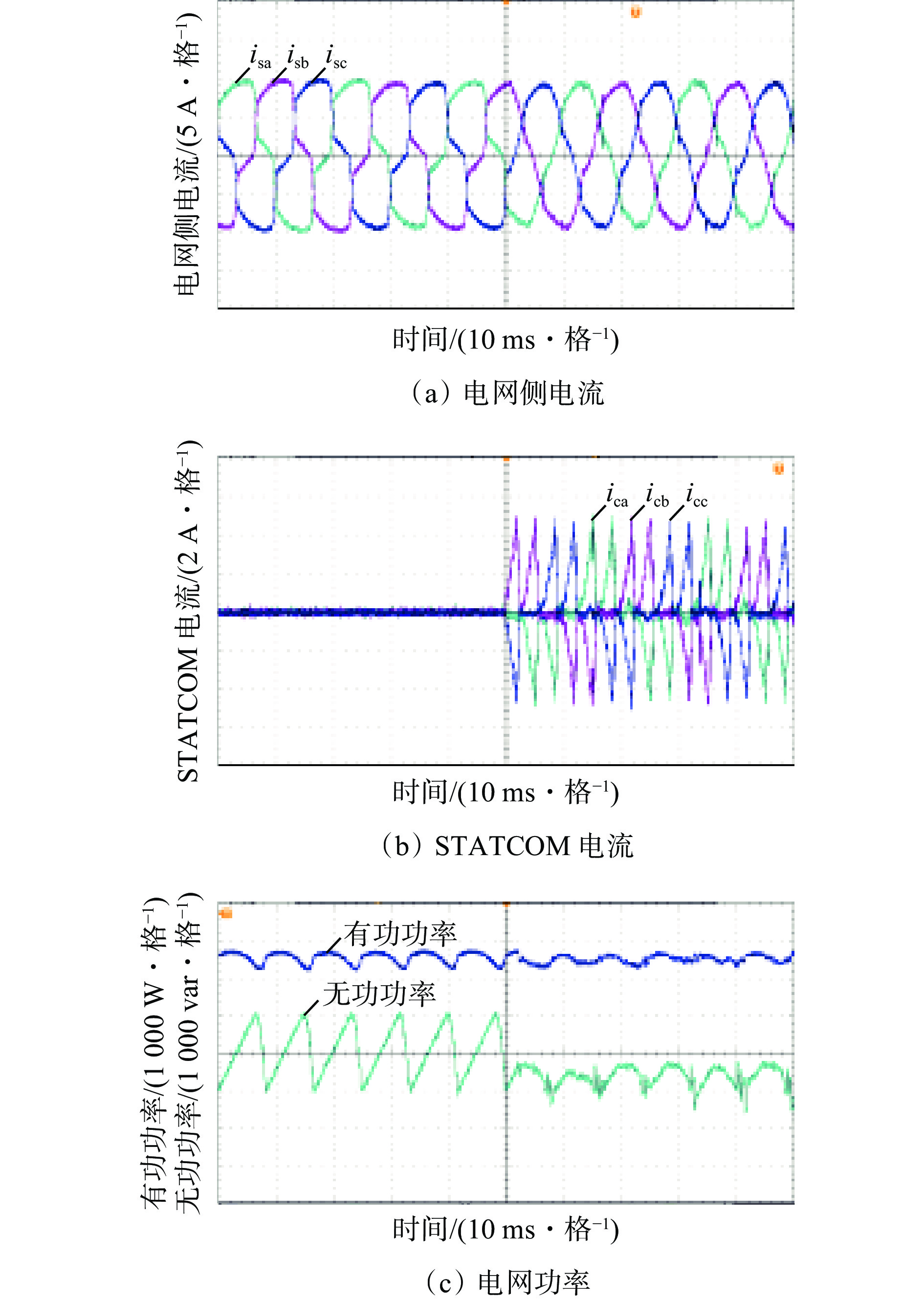
表 3 实验参数Table 3. Experimental parameters参数 值 电网线电压/V 380 滤波电感/mH 5 滤波电阻/Ω 0.1 直流侧电压/V 600 直流侧电容/μF 2 200 采样频率/kHz 20 开关频率/kHz 10 负载侧电阻/Ω 60 投入STATCOM前后电流、功率实验波形如图12所示。可看出在投入STATCOM前，由于非线性负载侧存在大量无功功率，电网侧三相电流严重畸变，在投入STATCOM后，由于向电网侧注入了反向的谐波电流和无功电流，电网侧电流基本呈正弦波形，降低了电网侧电流纹波；在投入STATCOM前，电网侧存在大量无功功率，在0～2 000 var之间波动，而在投入STATCOM后，无功功率基本降为0，同时有功功率基本维持不变。
![]()
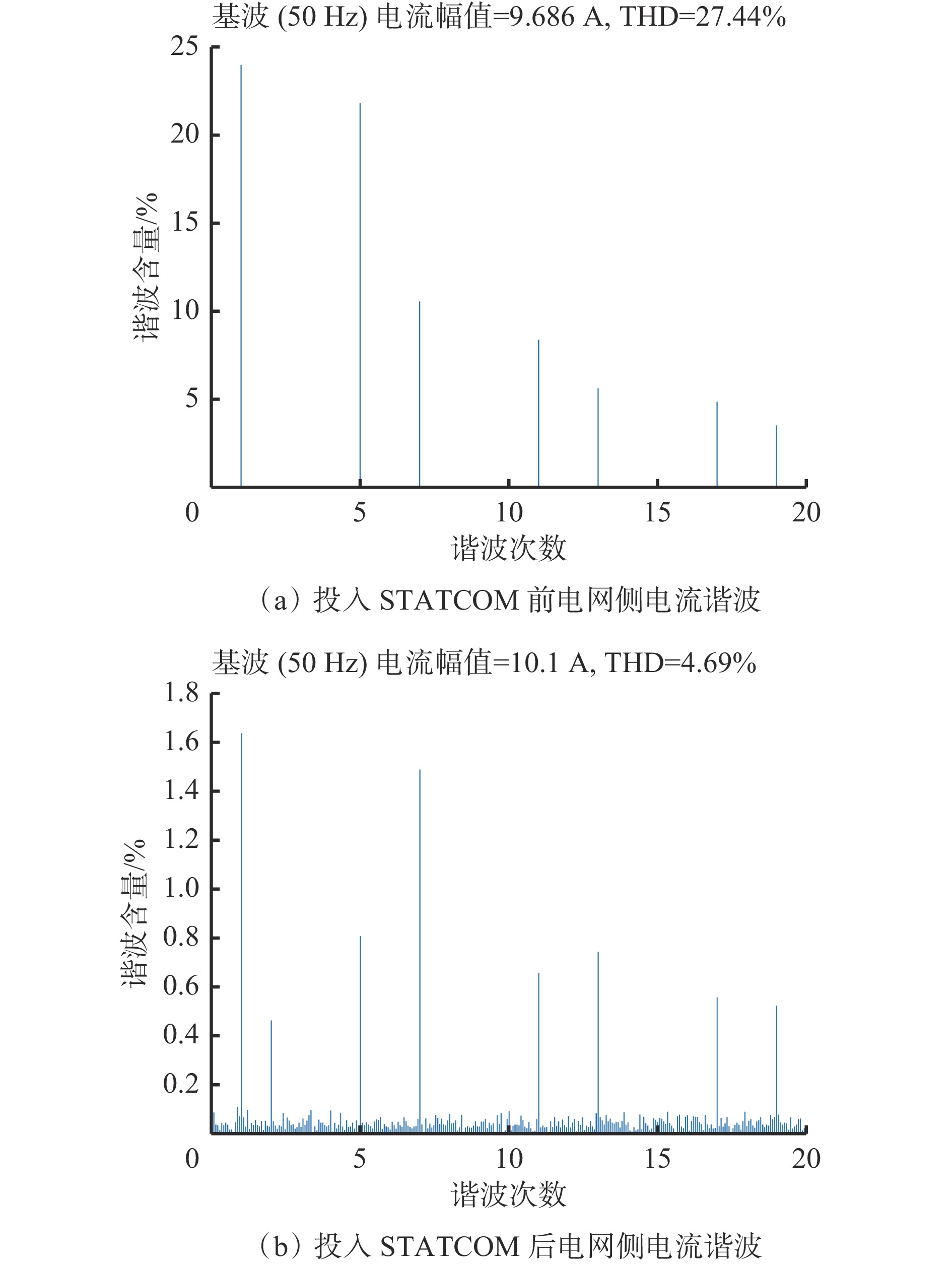
图 12 投入STATCOM前后电流、功率实验波形Figure 12. Experimental waveforms of current and power before and after adopting static synchronous compensator投入STATCOM前后电网侧电流谐波实验波形如图13所示。可看出在投入STATCOM前，电网侧电流存在大量谐波，THD为27.44%，而在投入STATCOM后电流THD降到4.69%，极大降低了电网侧电流谐波含量和THD。
![]()
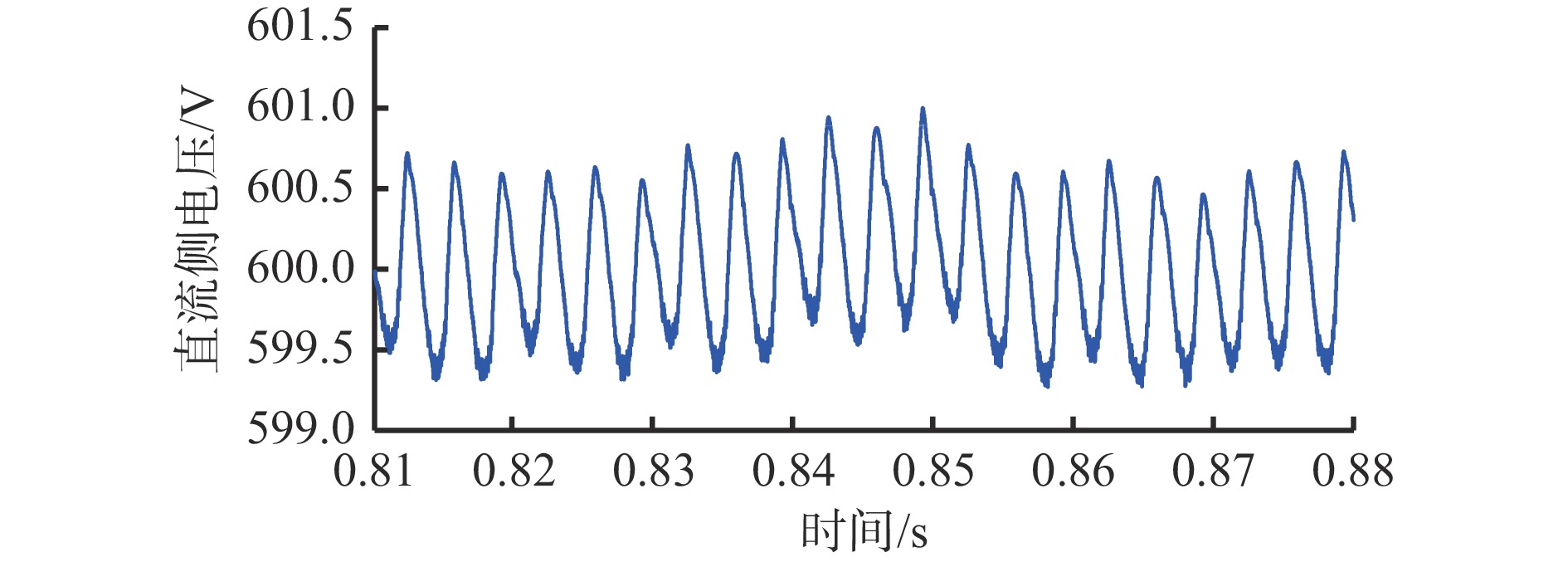
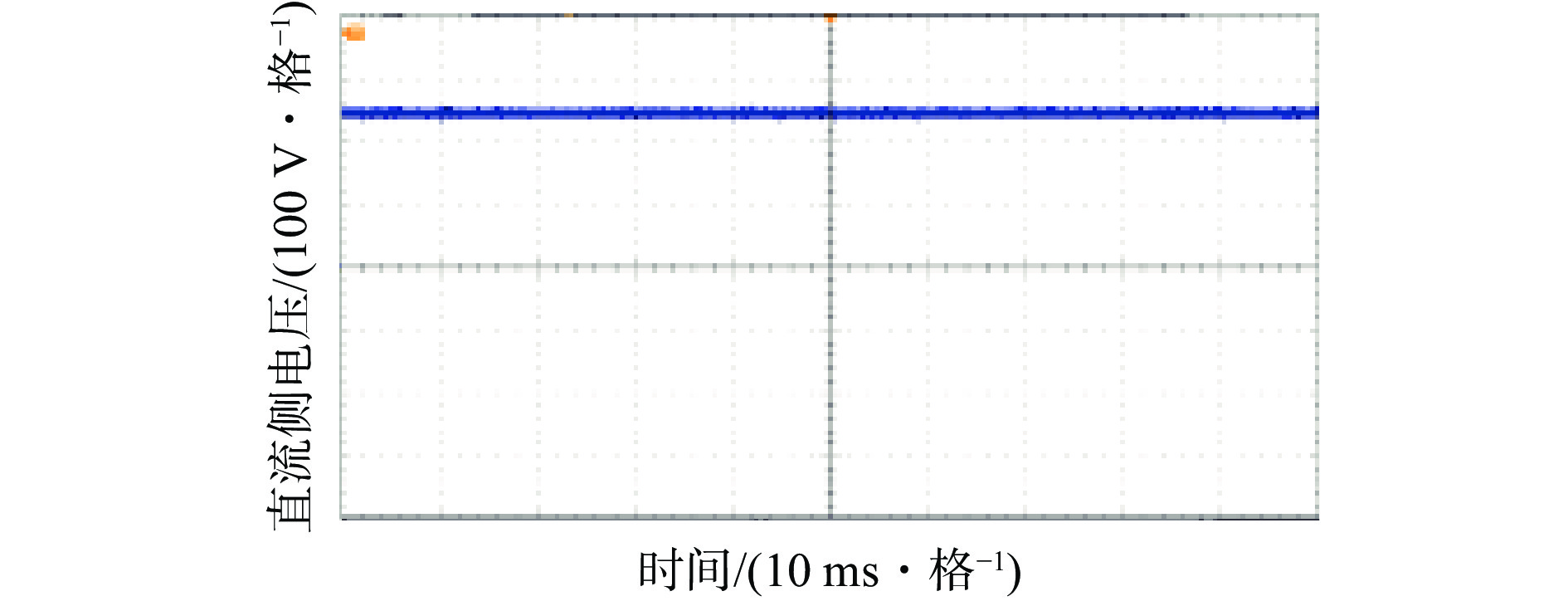
图 13 投入STATCOM前后电网侧电流谐波实验波形Figure 13. Experimental waveforms of grid side current harmonics before and after adopting static synchronous compensator投入STATCOM后直流侧电压实验波形如图14所示，可看出直流侧电压可以很好地稳定在参考值附近。
![]()
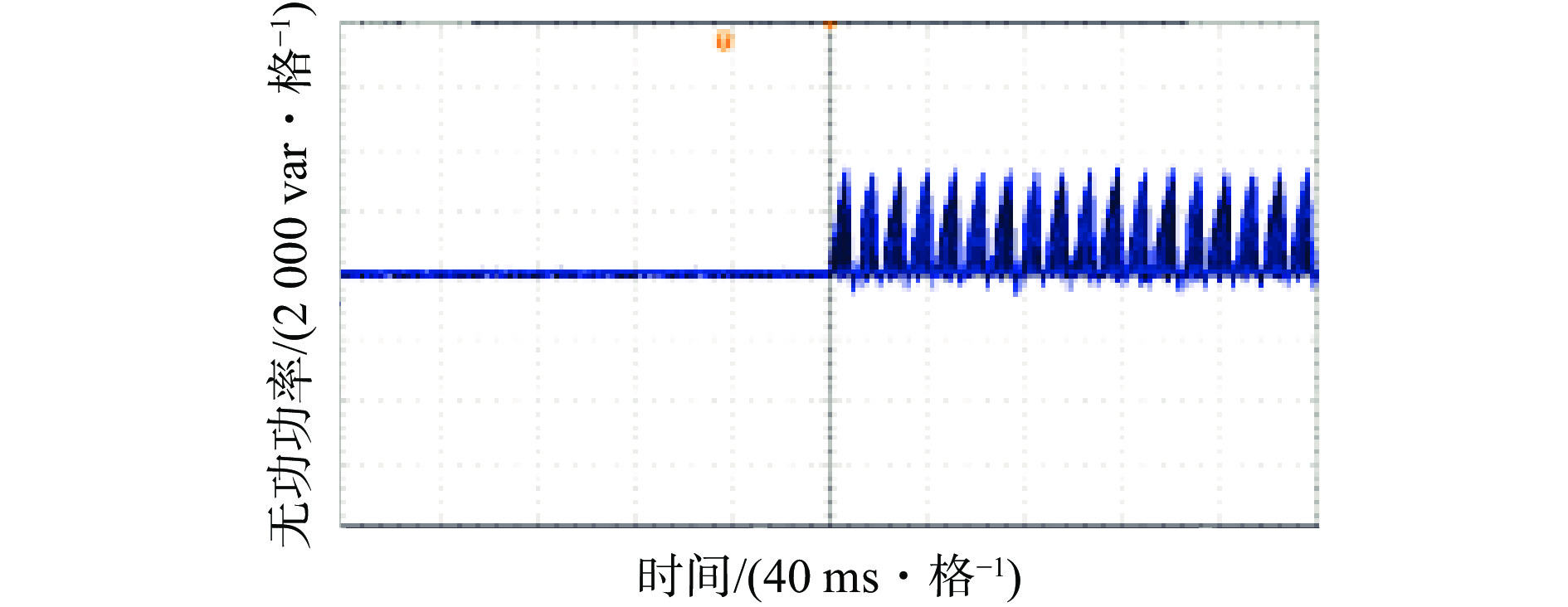
图 14 投入STATCOM后直流侧电压实验波形Figure 14. Experimental waveforms of DC-side voltage after adopting static synchronous compensator投入STATCOM前后STATCOM发出的无功功率实验波形如图15所示。可看出在投入STATCOM前，STATCOM发出的无功功率为0，负载所需要的无功功率由电网提供；在投入STATCOM后，STATCOM发出负载所需要的无功功率。
![]()
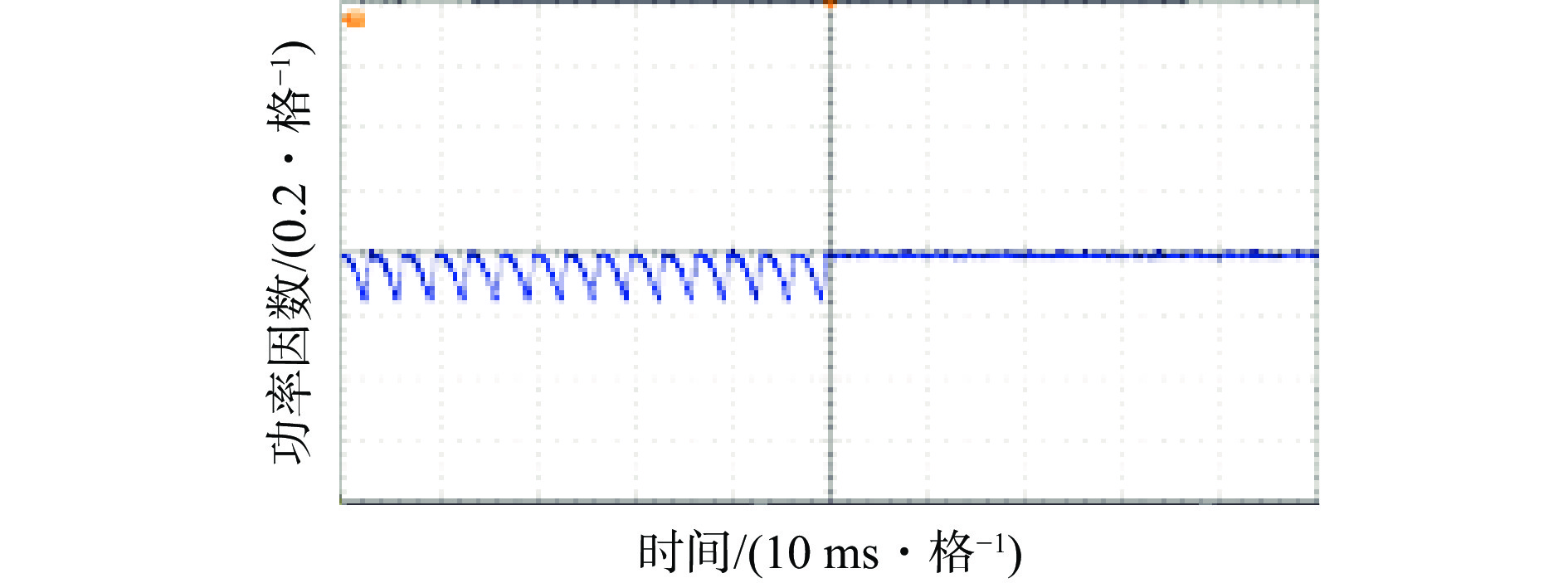
图 15 STATCOM发出的无功功率实验波形Figure 15. Experimental waveforms of reactive power sent by static synchronous compensator电网侧功率因数实验波形如图16所示。可看出在投入STATCOM前，由于电网侧存在大量无功功率，电网侧的功率因数在0.85～1之间不断波动；在投入STATCOM后，电网侧的功率因数基本恒定在1，表明STATCOM较好实现了无功补偿。
6. 结论
1） 采用ip−iq法提取电网侧谐波电流和无功电流，将其作为M2PC的参考电流。
2） M2PC选取每个扇区相邻2个有效矢量和零矢量合成的方式控制STATCOM，通过在每个扇区中计算3个矢量的占空比及最小化代价函数，得出最佳扇区及其对应的2个最佳有效矢量和零矢量的占空比。
3） 根据最佳有效矢量和零矢量的占空比，采用SVM方式分配开关脉冲，则IGBT在1个开关周期内只需开通或关断1次，实现固定的开关频率。
4） 实验结果表明：在投入基于M2PC的STATCOM前，电网侧电流畸变严重，电网侧无功功率波动大，电网侧功率因数存在波动且小于1；在投入基于M2PC的STATCOM后，电网侧电流THD大幅度降低，电网侧无功功率基本保持为0，电网侧功率因数稳定为1。
-
![]()
图 2 两电平STATCOM扇区及开关矢量分布
Figure 2. Sector and switching vector distribution of two-level ofstatic synchronous compensator
![]()
图 4 基于M2PC的STATCOM控制原理
Figure 4. Control principle of static synchronous compensator based on modulated model predictive control
![]()
图 5 基于M2PC的STATCOM控制流程
Figure 5. Control process of static synchronous compensator based on modulated model predictive control
![]()
图 6 M2PC脉冲分配（扇区1）
Figure 6. Pulse distribution of modulated model predictive control（sector 1）
![]()
图 7 投入STATCOM前后电压、电流仿真波形
Figure 7. Simulation waveforms of voltage and current before and after adopting static synchronous compensator
![]()
图 8 投入STATCOM前后电网侧电流谐波仿真波形
Figure 8. Simulation waveforms of grid side current harmonics before and after adopting static synchronous compensator
![]()
图 9 投入STATCOM前后电网侧有功功率和无功功率仿真波形
Figure 9. Simulation waveforms of grid side active and reactive power before and after adopting static synchronous compensator
![]()
图 10 投入STATCOM后直流侧电压仿真波形
Figure 10. Simulation waveforms of DC-side voltage after adopting static synchronous compensator
![]()
图 12 投入STATCOM前后电流、功率实验波形
Figure 12. Experimental waveforms of current and power before and after adopting static synchronous compensator
![]()
图 13 投入STATCOM前后电网侧电流谐波实验波形
Figure 13. Experimental waveforms of grid side current harmonics before and after adopting static synchronous compensator
![]()
图 14 投入STATCOM后直流侧电压实验波形
Figure 14. Experimental waveforms of DC-side voltage after adopting static synchronous compensator
![]()
图 15 STATCOM发出的无功功率实验波形
Figure 15. Experimental waveforms of reactive power sent by static synchronous compensator
表 1 STATCOM开关状态及开关矢量
Table 1 Switching status and switching vector ofstatic synchronous compensator
Sa Sb Sc 开关矢量 0 0 0 v0=0 1 0 0 v1=2Vdc/3 1 1 0 v2=Vdc/3+j$ \sqrt{3} $Vdc/3 0 1 0 v3=−Vdc/3+j$ \sqrt{3} $Vdc/3 0 1 1 v4=−2Vdc/3 0 0 1 v5=−Vdc/3−j$ \sqrt{3} $Vdc/3 1 0 1 v6=Vdc/3−j$ \sqrt{3} $Vdc/3 1 1 1 v7=0 
下载: 导出CSV
表 2 仿真参数
Table 2 Simulation parameters
参数 值 电网线电压/V 380 滤波电感/mH 2 滤波电感阻值/Ω 0.1 直流侧电压/V 600 直流侧电容/μF 2 200 采样频率/kHz 20 开关频率/kHz 10 负载侧电阻/Ω 20
下载: 导出CSV
表 3 实验参数
Table 3 Experimental parameters
参数 值 电网线电压/V 380 滤波电感/mH 5 滤波电阻/Ω 0.1 直流侧电压/V 600 直流侧电容/μF 2 200 采样频率/kHz 20 开关频率/kHz 10 负载侧电阻/Ω 60
下载: 导出CSV
-
[1] 王清亮,姚苗. 煤矿电能质量综合量化评价研究[J]. 工矿自动化,2015,41(2):42-46. WANG Qingliang,YAO Miao. Research of comprehensive quantitative evaluation of power quality of coal mine[J]. Industry and Mine Automation,2015,41(2):42-46.
[2] 王毅颖. 煤矿电网多谐波源分散抑制和APFs接入点优化研究[D]. 北京:中国矿业大学(北京),2017. WANG Yiying. Optimization research on distributed suppressing harmonic sources and placements of APFs in coal mine power grid[D]. Beijing:China University of Mining and Technology-Beijing,2017.
[3] 郭松梅. 煤矿电能质量综合治理研究[J]. 工矿自动化,2016,42(9):60-64. GUO Songmei. Research on power quality comprehensive treatment for coal mine[J]. Industry and Mine Automation,2016,42(9):60-64.
[4] 杨磊. 董家河煤矿电能质量测试分析与治理研究[D]. 西安:西安科技大学,2018. YANG Lei. Research on test analysis and treatment on power quality of Dongjiahe Coal Mine[D]. Xi'an:Xi'an University of Science and Technology,2018.
[5] 张淼,吴事煜,冯春寿,等. 一种新型谐振混合型有源电力滤波器[J]. 电力电子技术,2023,57(4):41-45. DOI: 10.3969/j.issn.1000-100X.2023.04.010 ZHANG Miao,WU Shiyu,FENG Chunshou,et al. A new resonant hybrid active power filter[J]. Power Electronics,2023,57(4):41-45. DOI: 10.3969/j.issn.1000-100X.2023.04.010
[6] 刘伟豪. 电网T型三电平静止无功补偿器的仿真与设计[J]. 电工技术,2018(19):41-44,47. LIU Weihao. Simulation and design of T type three level static var compensator in power grid[J]. Electric Engineering,2018(19):41-44,47.
[7] 韩冰,张宁宇,胡昊明,等. 考虑UPFC实时控制策略的电网功率调节能力研究[J]. 电力工程技术,2018,37(1):1-7. HAN Bing,ZHANG Ningyu,HU Haoming,et al. Control capability analysis of unified power flow controller considering real-time control strategy[J]. Electric Power Engineering Technology,2018,37(1):1-7.
[8] 祁琦,王宇,盛晓东,等. 基于串并联混合结构的动态电压恢复器研究[J]. 电工技术,2022(7):27-30. QI Qi,WANG Yu,SHENG Xiaodong,et al. Study on dynamic voltage restore based on series parallel hybrid structure[J]. Electric Engineering,2022(7):27-30.
[9] 刘威,季振东,孙毅超,等. 基于双频功率回路的星形级联H桥STATCOM不平衡补偿研究[J]. 中国电机工程学报,2023,43(9):3527-3538. LIU Wei,JI Zhendong,SUN Yichao,et al. Research on unbalance current compensation of star-connected cascaded H-bridge STATCOM based on dual-frequency power loop[J]. Proceedings of the CSEE,2023,43(9):3527-3538.
[10] 王明达,梁军,王广柱,等. 基于单星MMC的新型STATCOM及其控制策略[J]. 电力系统自动化,2015,39(18):108-113. WANG Mingda,LIANG Jun,WANG Guangzhu,et al. Control strategy of novel STATCOM based on modular multilevel converter with single-star configuration[J]. Automation of Electric Power Systems,2015,39(18):108-113.
[11] 秦祥栋,罗朋,王占立. 井下 1 140 V级联STATCOM关键技术的研究[J]. 煤炭技术,2014,33(10):212-214. QIN Xiangdong,LUO Peng,WANG Zhanli. Research on underground 1 140 V cascade STATCOM key technologies[J]. Coal Technology,2014,33(10):212-214.
[12] 赵建阳,张福民,龚博,等. 基于D−STATCOM 的煤矿供电系统功率平衡控制方法[J]. 煤炭学报,2017,42(增刊1):288-294. ZHAO Jianyang,ZHANG Fumin,GONG Bo,et al. Power balance control method based on D-STATCOM in coal mine power supply system[J]. Journal of China Coal Society,2017,42(S1):288-294.
[13] 王烨,牟宪民,齐琛. 三相电流源型STATCOM 的无锁相环控制策略[J]. 电力系统保护与控制,2015,43(14):131-136. WANG Ye,MU Xianmin,QI Chen. A control strategy of three-phase current source converter based STATCOM without PLL[J]. Power System Protection and Control,2015,43(14):131-136.
[14] 易桂平,胡仁杰,蒋玮,等. 电网电压不平衡对STATCOM的影响及抑制[J]. 电工技术学报,2014,29(6):238-247. YI Guiping,HU Renjie,JIANG Wei,et al. Influence of grid voltage unbalance on STATCOM and the countermeasure[J]. Transactions of China Electrotechnical Society,2014,29(6):238-247.
[15] 孙朝霞,张明敏,张晖,等. 配电网储能型 DSTATCOM 电能质量综合补偿策略[J]. 电力系统及其自动化学报,2023,35(4):75-84. SUN Zhaoxia,ZHANG Mingmin,ZHANG Hui,et al. Comprehensive power quality compensation strategy for energy-storage-based DSTATCOM[J]. Proceedings of the CSU-EPSA,2023,35(4):75-84.
[16] 於静,莫修权,徐楠. 矿山高压三电平ANPC变频器预测控制研究[J]. 工矿自动化,2016,42(10):85-90. YU Jing,MO Xiuquan,XU Nan. Research on predictive control for mine high-pressure three-level ANPC inverter[J]. Industry and Mine Automation,2016,42(10):85-90.
[17] 刘春喜,田宝奇,刘志乐,等. NPC型三电平并网逆变器自适应模型预测控制[J]. 电力系统及其自动化学报,2023,35(1):143-151. LIU Chunxi,TIAN Baoqi,LIU Zhile,et al. Adaptive model predictive control for NPC-type three-level grid-connected inverter[J]. Proceedings of the CSU-EPSA,2023,35(1):143-151.
[18] 王明金,苗长新,段森,等. 五电平级联H桥STATCOM改进模型预测电流控制[J]. 电力电子技术,2019,53(9):56-59. WANG Mingjin,MIAO Changxin,DUAN Sen,et al. Five-level cascade H-bridge STATCOM improved model predictive current control[J]. Power Electronics,2019,53(9):56-59.
[19] 李帅虎,向振宇,彭寒梅,等. 基于模型预测控制的SVC与STATCOM协调控制器[J]. 电网技术,2019,43(11):4218-4224. LI Shuaihu,XIANG Zhenyu,PENG Hanmei,et al. SVC and STATCOM coordination controller based on model predictive control[J]. Power System Technology,2019,43(11):4218-4224.
[20] 原亚雷,钊翔坤,徐高祥,等. 兼顾电压波动抑制的级联H桥STATCOM相间电压平衡控制策略[J]. 电网技术,2022,46(4):1494-1502. YUAN Yalei,ZHAO Xiangkun,XU Gaoxiang,et al. Clustered voltage balance control strategy of cascaded H-bridge STATCOM with suppressing DC voltage fluctuation[J]. Power System Technology,2022,46(4):1494-1502.
[21] TARISCIOTTI L,ZANCHETTA P,WATSON A,et al. Modulated model predictive control (M2PC) for a 3-phase active front-end[C]. IEEE Energy Conversion Congress and Exposition,Denver,2013:1062-1069.
-
期刊类型引用(1)
1. 王伟，程卫健，张德正. 基于PSO和滑模观测器的永磁同步电机预测控制. 煤矿机械. 2024(05): 192-195 . 
百度学术
其他类型引用(2)
计量
- 文章访问数: 615
- HTML全文浏览量: 64
- PDF下载量: 24
- 被引次数: 3
