0.   引言

随着煤矿开采深度的增加，地应力逐渐增加，动力灾害愈加频繁，严重威胁煤矿安全生产。煤矿深部典型动力灾害主要包括冲击地压、煤与瓦斯突出和煤岩瓦斯复合动力灾害，具有突然、急剧、猛烈等特点^[1]。目前对于其形成过程及演化机制认识不清，灾害前兆信息辨识技术落后，但普遍认为应力是导致动力灾害的主要因素之一。因此，对煤层应力状态进行有效监测，是实现监测预警的基础^[2-3]。

目前煤层应力状态监测预警方法包括电磁辐射法^[4-5]、CT法^[6]、电阻率法^[7]、微震法^[8]等。电阻率作为煤岩重要的物理电性参数，可以很好地反演出生产现场的煤岩裂隙发育程度^[9]。基于电阻率差异探测的电阻率法精度高^[10]、噪声小，可突破由点到面的监测，目前已被广泛应用于煤矿生产现场。

煤岩动力灾害的产生与煤岩应力集中息息相关。对于电阻率监测预警技术而言，电阻率与煤岩受载破坏状态之间的关系是基础^[11]。因此，对煤样电阻率变化规律的研究有助于实现煤样破坏精准探测。Wang Yungang等^[12]研究了不同型煤在单轴压缩下的电阻率变化情况，发现受载煤的电阻率变化能够很好地反映型煤微裂隙的产生、扩展和贯通的情况，并且指出在单轴压缩下煤的压缩、弹性阶段以电子导电性为主，塑性、破坏阶段以离子导电性为主。Sun Qiang等^[13]研究了岩石单轴破坏的电阻率变化规律，发现电阻率随着岩石晶格破坏伸展的过程而发生剧烈变化，且剧变临界点在单轴压缩峰值的75%～85%之间。Chen Peng等^[14]指出煤样导电分为离子导电和电子导电2种，离子导电为主的煤样经历了缓慢上升到加速上升的变化过程，而电子导电为主的煤样则经历先减小后增加的V型变化；煤样电阻率的突变（弹性阶段变为塑性阶段）发生在峰值应力66%～87%之间，归一化电阻率最大可达3.49。李术才等^[15]建立了砂岩加载破坏的声发射−电阻率测试系统，确定了砂岩在单轴破坏过程中的声发射−电阻率变化规律，推导了基于声发射和电阻率的综合损伤模型，提出了砂岩破坏的判别标准和前兆特征。陈耕野等^[16-17]研究了氯化钠溶液石灰岩、砂岩加载破坏过程的电学效应，通过数值拟合方法提出了基于电阻率的砂岩应力−应变过程的状态方程并进行了验证。

上述文献集中于煤岩电阻率变化规律及机制研究，而对于不同加载阶段应力与电阻率的相互作用关系研究相对较少。因此，本文选取煤样进行实验室加载破坏，研究其破坏时电阻率与应力、损伤的变化规律、耦合规律及相关性，为电阻率法监测煤岩动力灾害现象的应用提供理论支持。

1.   实验方案

1.1   煤体电阻率加载测试系统

煤体电阻率加载测试系统主要由加载系统与电阻率信息采集系统组成，如图1所示，其中加载系统包括压力机、加载头及载荷控制系统3个部分。本文采用YAW−600微机控制电液伺服压力试验机进行加载控制。压力机最大载荷达600 kN，压头刚度为5 000 kN/mm，最小分辨力为3 N，最小分辨位移为0.3 μm，采样频率为1 kHz。采用等速应力、等速位移、等速应变、力保持和位移保持等加载方式实时显示应力−应变曲线、载荷−时间曲线。

图  1  煤体电阻率加载测试系统

Figure  1.  Coal resistivity loading test system

下载: 全尺寸图片 幻灯片

电阻率信息采集系统为VICTOR 4080 LCR，最高测试频率为100 kHz，测试电平为0.6 Vrms。LCR测试仪语煤样连接方式采取正负极外接导线分别缠绕煤样两端。导线缠绕在距离煤样上下端10 mm处，避免端头破坏造成导线损坏。LCR测试仪通过USB接线与PC连接，利用串口软件连续采集数据，并导出为Excel文件进行处理。电阻率测试频率为100 kHz。

1.2   煤样品制备

煤样品取自河南省永城市矿区的车集煤矿Ⅱ₂煤层，煤质主要为无烟煤。据现场鉴定结果，煤层瓦斯含量为0.06～14.49 m³/t，瓦斯超限情况较为严重。经过机械加工，将煤样切割为ϕ 50 mm×100 mm的圆柱形标准煤样，参数见表1。

表  1  煤样参数

Table  1.  Sample parameters

编号	长/mm	宽/mm	质量/g	密度/（g·m−3）
1	97.88	49.60	277.31	1.4670
2	98.02	49.08	286.28	1.5445
3	100.10	50.10	319.87	1.6218

下载: 导出CSV 

| 显示表格

1.3   加载方案

将待测型煤样放置在加载系统上，轻轻压紧后测试顶端平整度；煤样两端面涂抹导电膏，在样品两端布置电极板并用绝缘板隔离，通过导线连接电极板至LCR测试仪；打开LCR数字电桥测试仪，热机30 min，观察LCR数字电桥示数，直至稳定；开启压力机，设置加载方案为单轴加载，控制方法为位移加载，加载速率为3 μm/s；启动LCR测试仪，布置测线至主机，随后开启压力机测试整个加载过程中的电阻率变化情况。

1.4   电阻率相关参数

在加载破坏过程中，对单一电阻率的关注度较低，一般更关注电阻率随应力变化情况。为了使电阻率的变化量更加明显，需对不同煤样的电阻率进行归一化处理。

式中：λ为归一化后的电阻率，随着应力加载水平的增加而发生改变；ρ为加载过程的电阻率；ρ₀为初始时刻的电阻率。

为了分析评价煤样应力状态变化快慢，需要进一步对电阻率的时序变化情况进行分析。

式中：$ {{{\mathrm{d}}\lambda } \mathord{\left/ {\vphantom {{{\mathrm{d}}\lambda } {{{{\mathrm{d}}}}t}}} \right. } {{\mathrm{d}}t}} $为煤样电阻率的突变能力，负值表示突减，正值表示突增；t为时间；ρ_i为i时刻的电阻率；ρ_i−1为i−1时刻的电阻率。

2.   实验结果与分析

2.1   不同阶段煤岩电阻率−应力规律

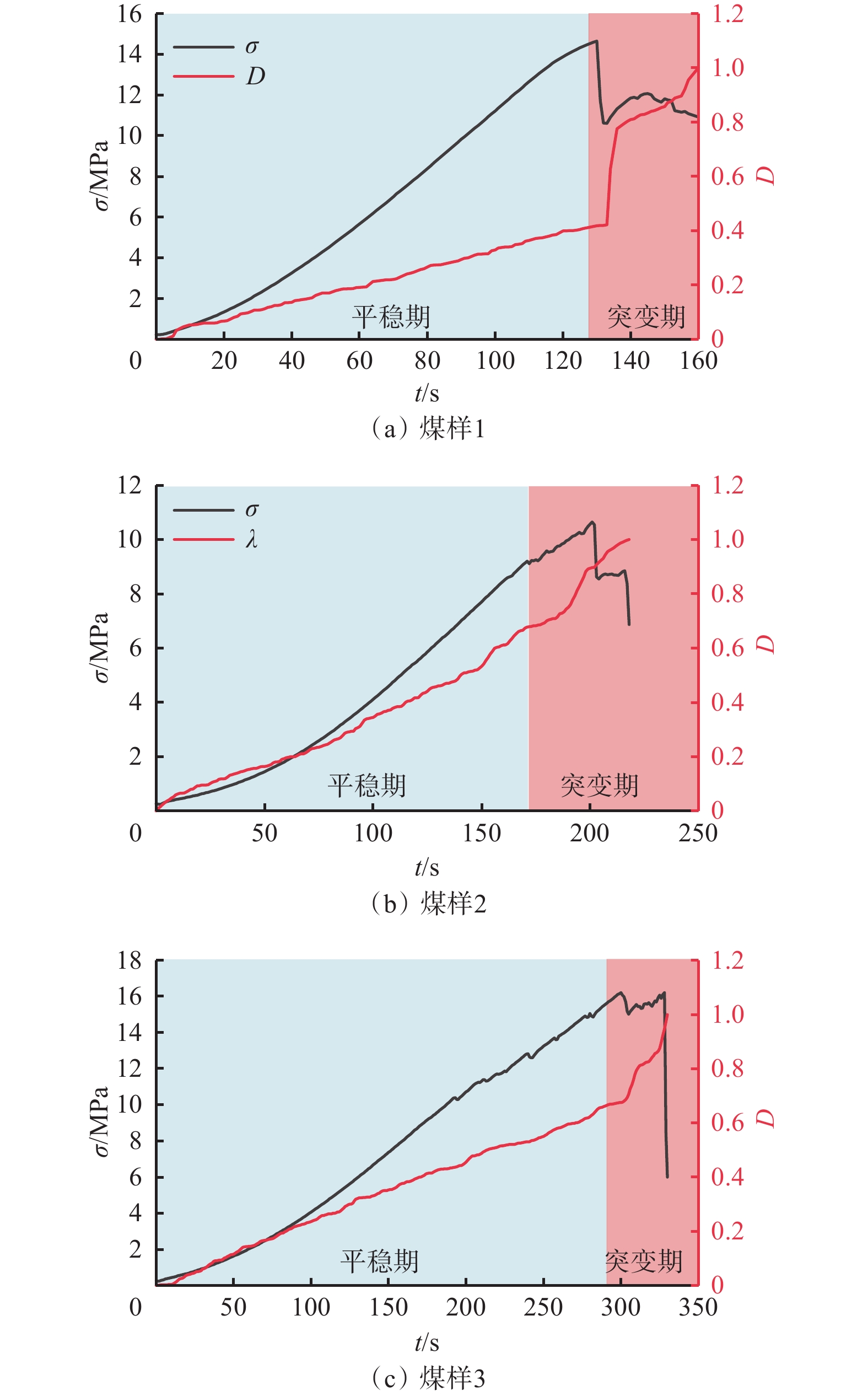
对3个煤样进行单轴压缩破坏实验，其应力$ \sigma $、电阻率$ \lambda $随时间t变化曲线如图2所示。可看出应力与电阻率均有良好的对应关系。电阻率在煤样压缩阶段均呈不断减小的趋势，而在弹性阶段与塑性阶段变化速度降低，各煤样电阻率最低值为0.8左右。在破坏阶段，电阻率随着煤样的破坏均发生突增，增长幅度均大于0.02。值得注意的是，3块煤样在应力峰值均没有立即破坏，而是进入了具有一定支撑能力的峰后阶段，在这一阶段煤样仍存在一定的承载能力，电阻率变化量降低，这说明电阻率受煤样裂隙扩展的影响，伴随着大破坏的产生才出现电阻率的突增。

图  2  应力−电阻率−时间曲线

Figure  2.  Stress-resistivity-time curves

下载: 全尺寸图片 幻灯片

2.2   不同阶段应力−电阻率相关性分析

在岩石物理学的研究过程中，Archie假设岩石基质为绝缘体^[18]，岩体的导电性由岩体中连通孔的孔隙水决定，并忽略了电双性的作用，得到了阿尔奇公式：

式中：F为地层因子；I₁为电阻率指数；ρ_w为孔隙水的电阻率；$\alpha $为岩石的孔隙率；m为胶结指数；S_w为岩体的含水率；n为饱和度指数。

由式（3）可知，煤样电阻率主要受煤样含水率及孔隙率共同作用影响。电阻率随着煤样孔隙率在应力加载过程中的变化而变化^[19]。因此，为进一步分析应力变化对电阻率的影响，采用二次多项式函数对不同阶段应力−电阻率进行数值模拟，结果如图3所示。可看出不同煤样在压缩阶段、弹性阶段、塑性阶段的电阻率与应力相关性较好；而在破坏阶段，电阻率与应力的相关性较差，这是由于破坏后孔隙、裂隙大范围变化，电阻率点较为分散且没有明显的对应关系。

图  3  应力−电阻率耦合曲线

Figure  3.  Stress-resistivity coupling curves

下载: 全尺寸图片 幻灯片

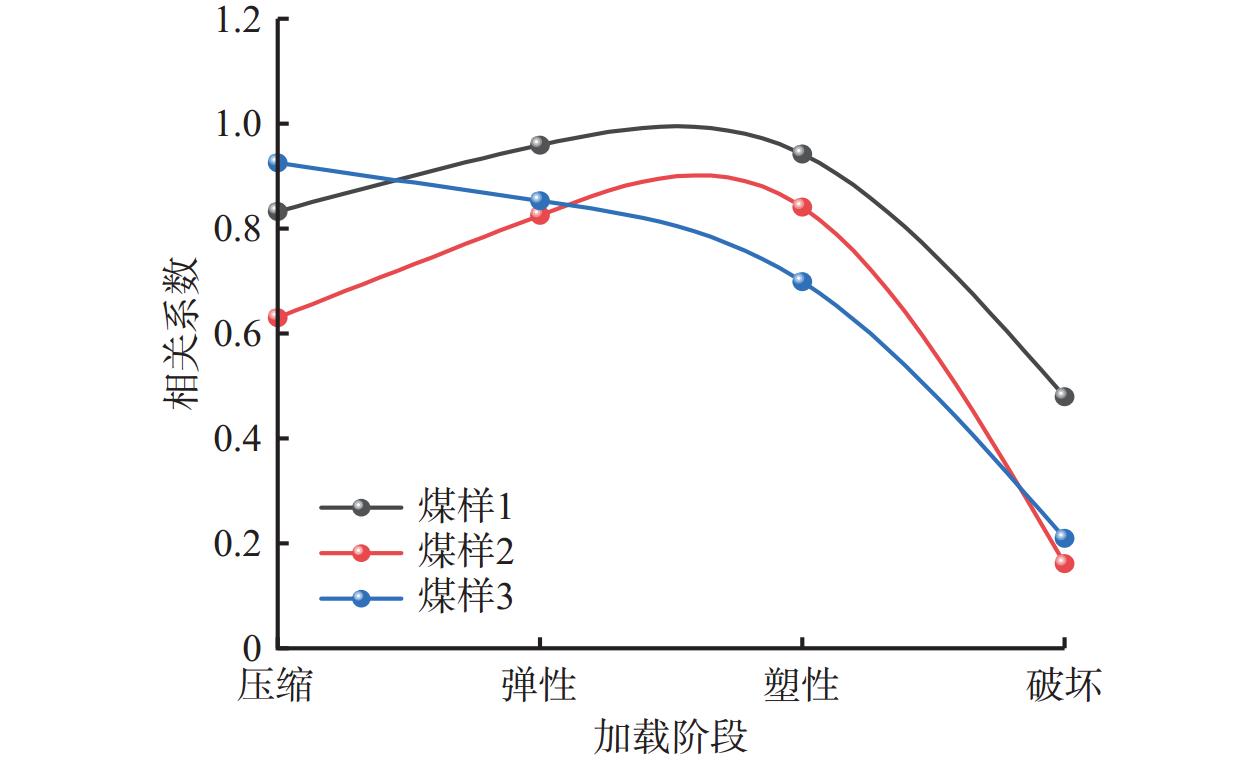
各煤样在不同阶段的应力−电阻率相关系数如图4所示。可看出在压缩、弹性、塑性3个阶段，应力−电阻率相关系数均大于0.6，表现出强相关性；而在破坏阶段，应力−电阻率相关系数小于0.4，为弱相关性。煤样电阻率的变化受到孔隙率的影响。在煤样压缩阶段，孔隙在应力作用下逐渐闭合；在煤样弹性阶段，煤样中发生弹性变形，孔隙率变化较小；在煤样塑性阶段，煤样逐渐出现微破坏，微孔隙得到发育。这3个阶段主要涉及微孔隙的闭合及发育，并没有大孔隙的扩展，因此在这3个阶段电阻率变化相对较小，电阻率与应力有着良好的对应关系。而在破坏阶段，煤样在应力作用下发生了猛烈的破坏并伴随着大裂隙的产生，此时电阻率变化受到大裂隙影响，与应力的相关性降低。

图  4  各煤样在不同阶段的应力−电阻率相关系数

Figure  4.  Stress-resistivity correlation coefficient across samples at different stages

下载: 全尺寸图片 幻灯片

上述分析表明电阻率在应力作用下具有明显的变化趋势，且这种变化趋势具有阶段变化的特性。在煤层开采过程中，煤层受到采动应力影响发生变形，此时煤层应力变化将会导致煤层电阻率发生变化。而不同阶段电阻率的变化趋势是对煤层应力状态进行监测的理论依据。由此可见，高电阻率区域对应煤层较为危险的区域。

2.3   电阻率变化率

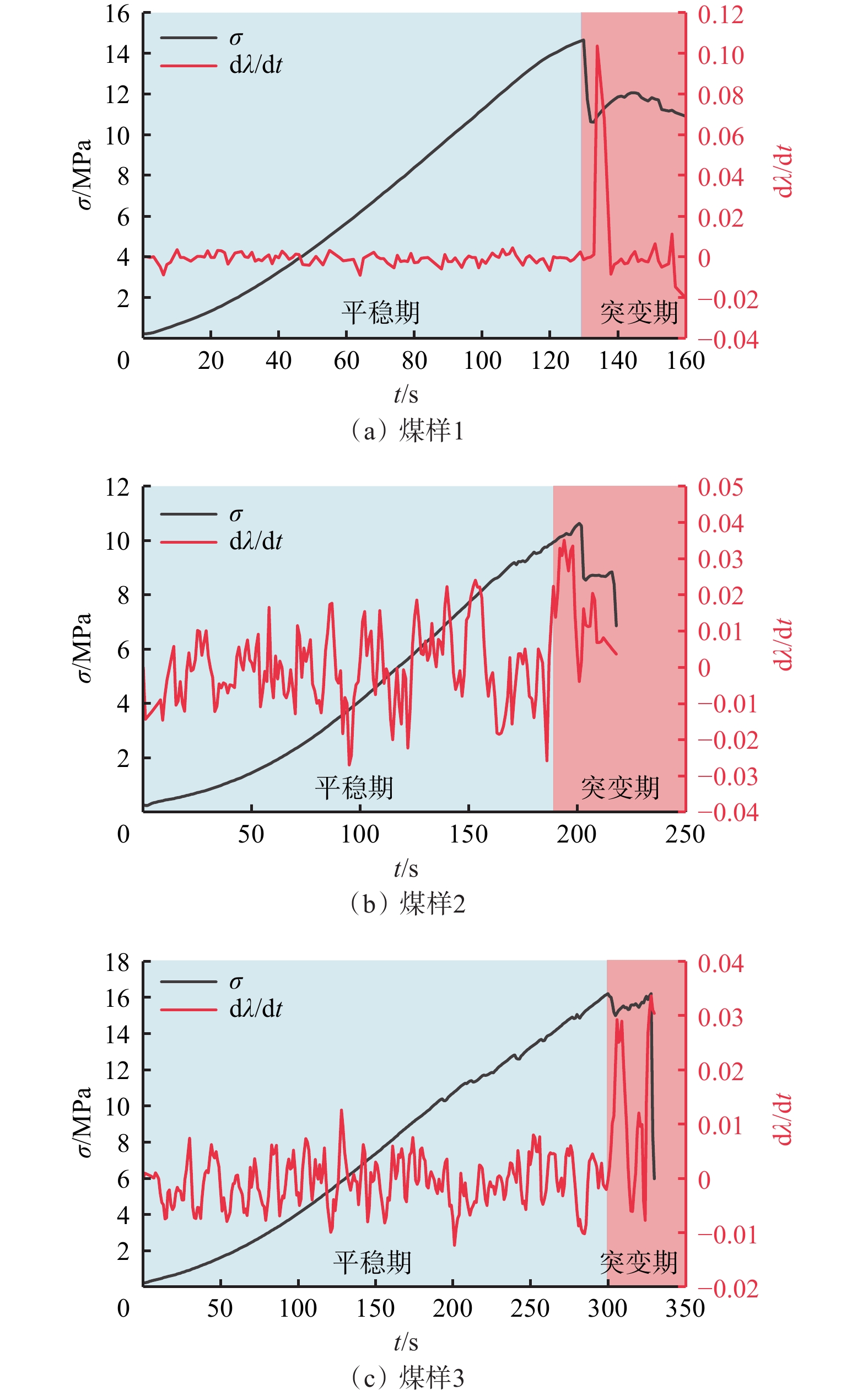
对3个煤样电阻率变化率进行分析，结果如图5所示。

图  5  电阻率变化率随时间变化曲线

Figure  5.  Curve of resistivity change rate with time

下载: 全尺寸图片 幻灯片

由图5可看出，电阻率变化率在整个加载过程中均表现出一定的波动性，且在压缩、弹性、塑性阶段之前波动较小；而在破坏阶段发生突增。因此，将变化率时序变化可以分为平稳期与突变期2个部分。各煤样电阻率变化率在平稳期的变化均小于0.01，而在突变期电阻率变化率均大于0.02。

在外界压力作用下，煤样内部孔隙存在大量的非均匀破坏，这些破坏对煤样导电通道造成影响，进而导致波动性变化。因此，波动性大小表明了煤样微破坏频率高低。电阻率变化率可以作为煤样破坏时刻的判断指标，其值设为0.02。

2.4   基于电阻率的损伤变化

M.Kachanov^[20]认为损伤实际上是材料在外界作用下有效承载面积不断减小的过程，将损伤定义为有效承载面积与初始面积的比值。假设煤的损伤D是连续破坏的，内部微元体随着破坏的产生逐渐增加。

式中：N^*为材料受损后的面积；N_m为材料初始无损的横截面积。

按照损伤理论^[21]，煤样的应力方程满足：

式中：E为材料的弹性模量；$ \varepsilon $为煤样应变。

一般认为煤样力学参数分布满足Weibull分布^[21]，岩石应力−应变曲线的本构方程为

式中：$ {\varepsilon _0} $为初始应变；k为Weibull分布的形状系数。

利用电阻率变化累积量对煤样的细观破坏进行定量描述。则电阻率引起的损伤变化为

式中：R为某应力状态下煤样破坏引起的电阻率变化累积量；R_m为煤样完全破坏后的电阻率总变化量。

将式（7）代入式（5），得到基于电阻率的煤样应力模型：

因此，各煤样损伤变化曲线如图6所示。可看出各煤样在加载的稳定阶段损伤D呈线性增加，此时煤样的损伤处于稳定增加阶段。随后煤样进入突变期发生大变形后，损伤发生较明显的突变。对比损伤的变化曲线可以发现，各煤样在加载前期出现了呈线性的缓慢增加趋势，而在塑性阶段和破坏阶段电阻率迅速增加，最终在完全破坏后损伤变为1。

图  6  基于电阻率的煤样损伤变化曲线

Figure  6.  Coal damage variation curves based on resistivity

下载: 全尺寸图片 幻灯片

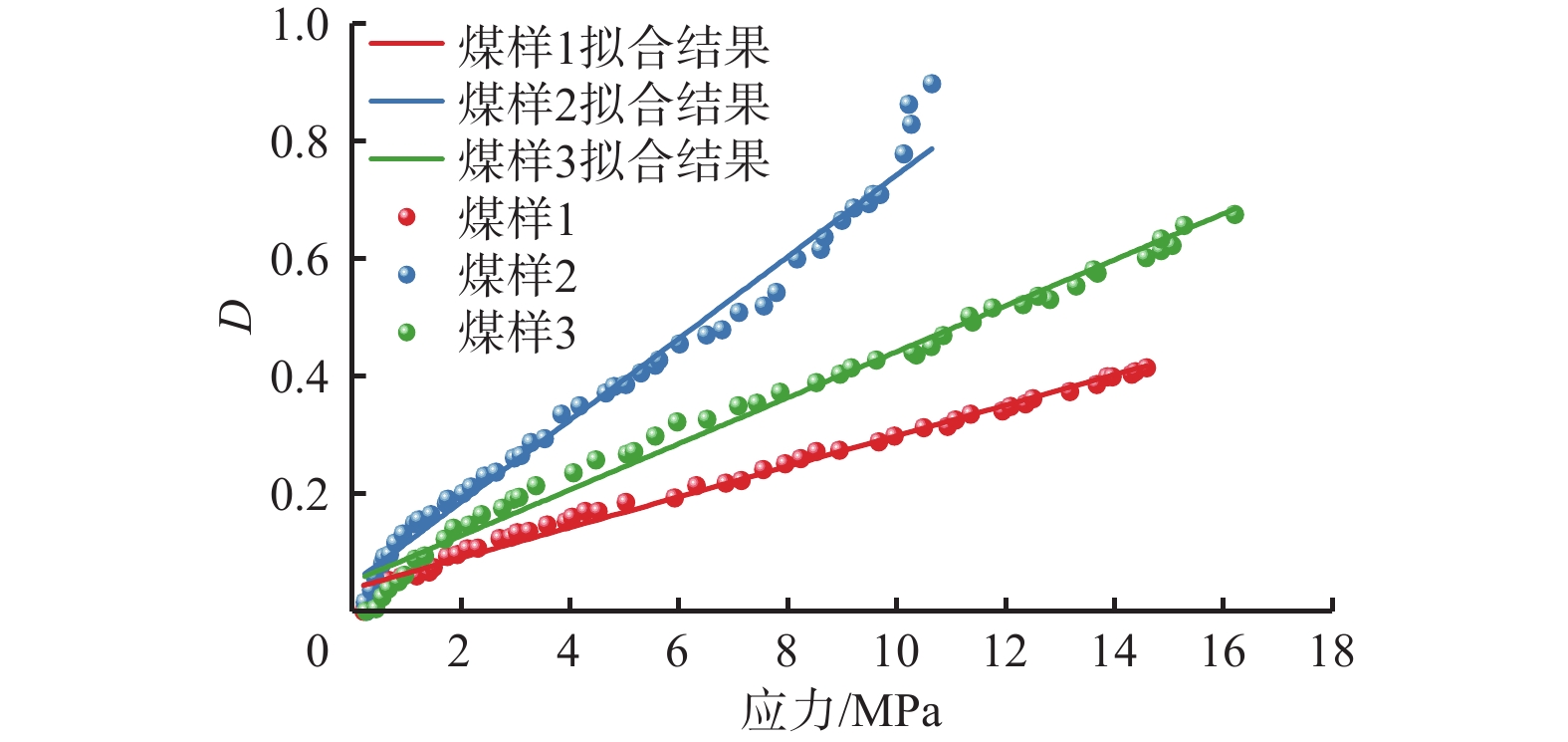
煤样发生破坏阶段前应力与损伤之间的相关性如图7所示。可看出应力与损伤的相关性较好，属于强相关性。煤样破坏前内部损伤为微小变化，此时电阻率主要受到微孔隙变化影响，此时电阻率表征的损伤变化相关性较好。而在破坏时刻伴随着大断裂的产生、贯通，损伤显著增加。煤样的裂纹扩展与滑移破坏是导致煤样破坏的主要因素，而煤样破坏性裂隙出现是电阻率及损伤快速变化的根本原因。

图  7  破坏前应力与损伤相关性

Figure  7.  Correlation between stress and damage before failure

下载: 全尺寸图片 幻灯片

3.   煤样破坏损伤变化机制

3.1   煤岩电阻率导电通道

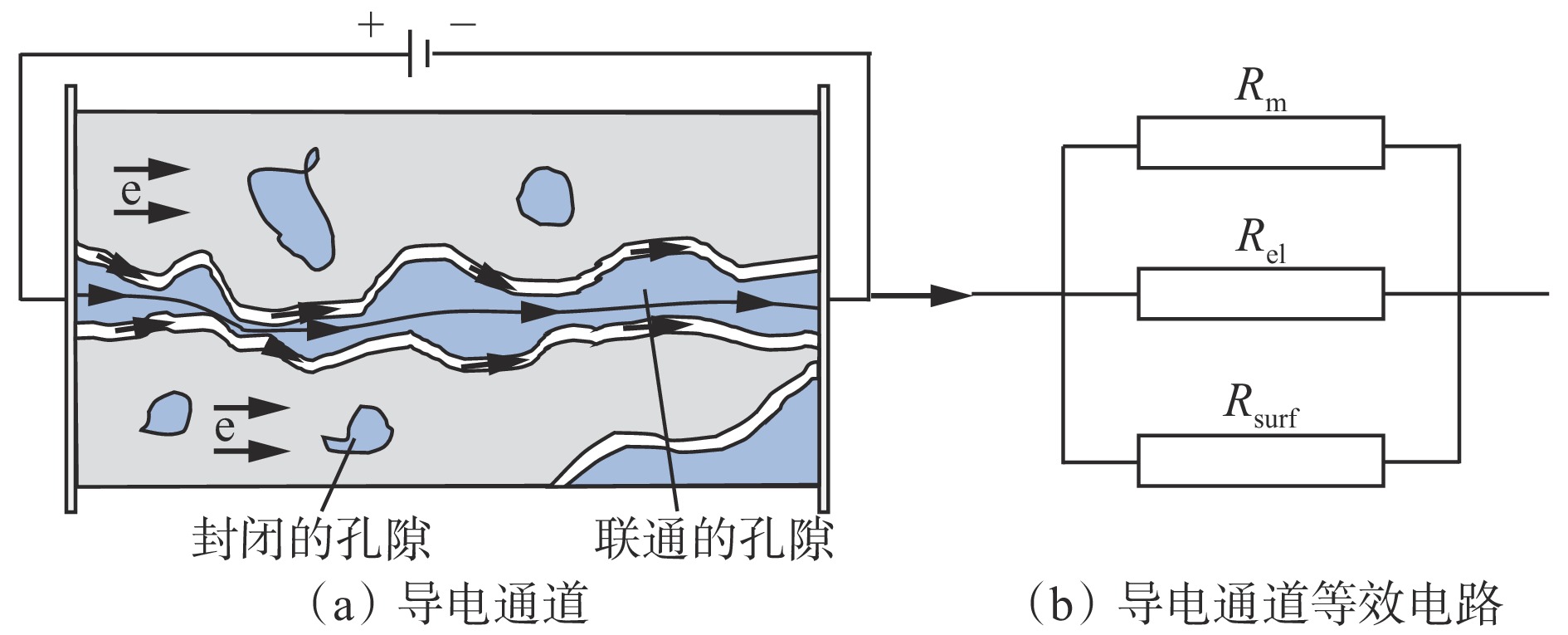
固体介质的导电可以分为电子导电与离子导电，前人发现煤样基质导电主要为电子导电形式^[14]。同时，考虑煤样内部孔隙中含有大量的矿物质、水分，在内部孔隙也存在离子导电。而在孔隙表面，受限于带电粒子浓度梯度的变化，还存在电双层（Electric Double Layer，EDL）作用。因此，煤的导电通道大致可以分为基质电子导电、孔隙水溶液导电及EDL层离子导电3条导电通道，如图8（a）所示，其等效电路如图8（b）所示。

由于电场的作用，煤样及孔隙水中的带电介质通过以上3个导电通道传导。因此，煤样的电阻率为

式中：R'为煤样的电阻率；R'_m为基质的电阻率；R_el为孔隙水的电阻率；R_surf为电双层的电阻率。

孔隙水对整体电导性的影响主要体现在孔隙水的盐度。同时，在实际生产中煤样内部并不是饱和水，大部分孔隙被空气、瓦斯等气体占据，煤样内部的水分主要以束缚水为主。因此，在分析煤样电阻率变化时，上述3个导电通道要综合考虑。

图  8  多孔介质的导电通道

Figure  8.  Schematic diagram of conductive pathways in porous media

下载: 全尺寸图片 幻灯片

3.2   受载破坏电阻率−应力−损伤耦合机制

电阻率在不同阶段的变化趋势有显著变化。在压缩阶段和弹性阶段电阻率保持不变或缓慢增加，在塑性阶段电阻率增加明显，最终达到峰值。煤样在加载过程中电阻率具有一定的波动性，这与文献[22]的实验现象具有一致性。

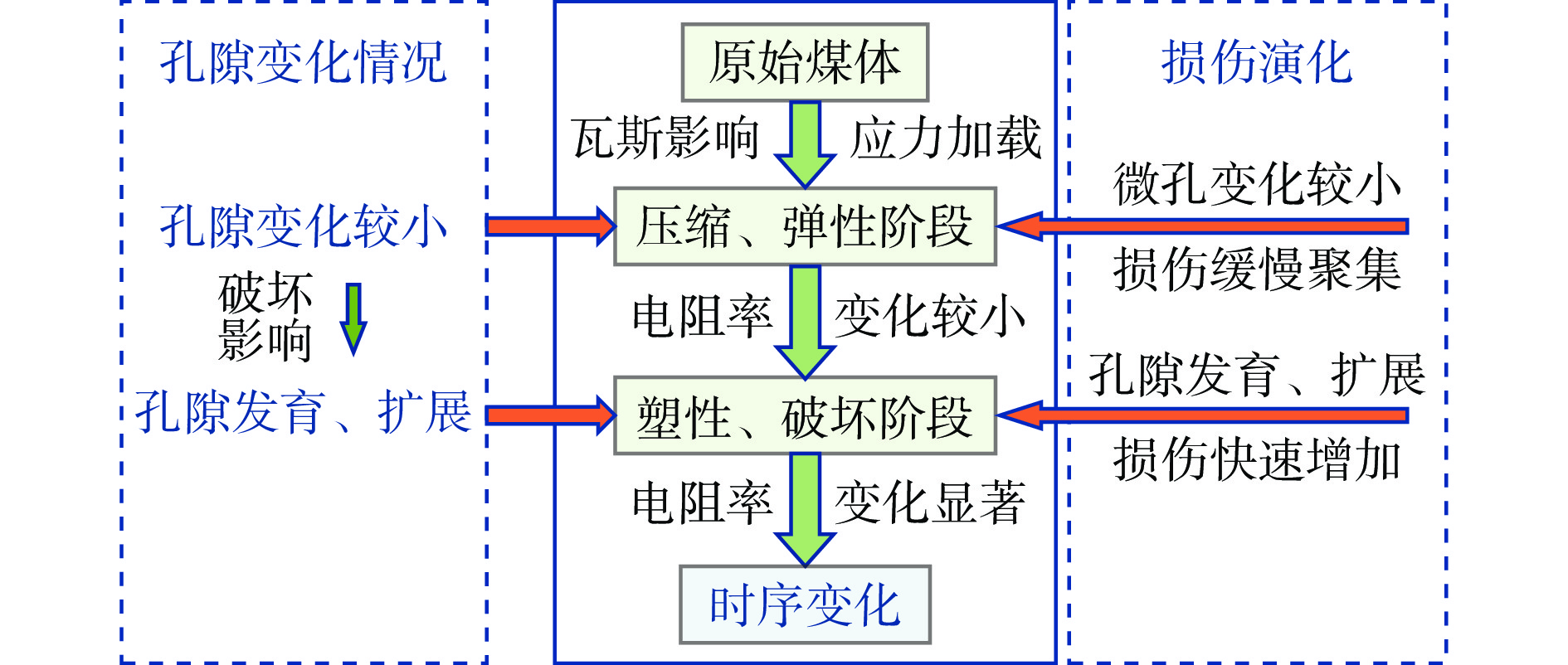
煤样破坏过程的电阻率−应力−损伤耦合机制如图9所示。可看出在不同阶段的主控因素并不相同。在塑性阶段之前，煤样内部主要是微孔隙的闭合，煤样主要发生弹性应变，因此电阻率的波动是由微孔引起的，此时电阻率更多取决于煤样基质本身的导电性质；而在塑性阶段和破坏阶段则是由孔隙扩展、贯通及断裂破坏引起的。同时，煤样内部具有一定的含水性，当裂隙网络贯通发育后，水分迁移通道逐渐形成，随后在大破坏形成后电阻率迅速增加。

图  9  煤样破坏电阻率−应力−损伤耦合机制

Figure  9.  Mechanism of resistivity-stress-damage coupling in coal failure

下载: 全尺寸图片 幻灯片

在这个过程中，损伤反映了煤样破坏程度，其中在压缩、弹性阶段孔隙变化缓慢，此时损伤呈缓慢线性积累。而随着塑性、破坏阶段煤样应力的增加，内部孔隙发育并迅速扩展，煤样内部破坏速度增加，电阻率发生显著变化，对应损伤快速增加。

4.   结论

1） 通过测试煤样加载破坏过程的电阻率变化，确定了不同阶段应力−电阻率相关性、电阻率变化率变化规律，并基于电阻率确定了煤样损伤变化规律。

2） 电阻率在煤样压缩阶段呈不断减小的趋势，而在弹性阶段与塑性阶段这一趋势变化降低，在破坏阶段随着煤样的破坏发生突增。

3） 在压缩阶段、弹性阶段、塑性阶段，电阻率与应力相关性较好，表现出强相关性；在破坏阶段，由于破坏后孔隙、裂隙的大范围变化，电阻率点较为分散且没有明显的对应关系，为弱相关性。

4） 电阻率变化率在整个加载过程中表现出一定的波动性，总体可分为平稳期与突变期，且在压缩、弹性、塑性阶段之前波动较小并基本保持一致；而在破坏阶段电阻率变化率发生突增；平稳期电阻率变化率变化均小于0.01，而突变期电阻率变化率均大于0.02。

5） 在塑性阶段之前，煤样主要发生弹性应变，电阻率波动是由微孔引起的，此时微孔隙引起的损伤决定煤样电阻率变化；而在塑性阶段和破坏阶段则是由孔隙扩展、贯通及断裂破坏引起的。同时，煤样内部具有一定的含水性，在煤样裂隙贯通后水分得以相互连接，随后在大破坏形成后电阻率迅速增加。