A pose recognition method for warehouse cleaning robots based on extended Kalman filtering
-
摘要: 煤矿水仓巷道光照强度不均匀且结构化特征明显，传统基于视觉的机器人位姿识别方法识别不准确，而单一的机器人定位技术如自适应蒙特卡洛（AMCL）方法随着清仓机器人的长时间运行，输出的位姿信息存在较大累计误差，易出现煤泥清理不干净、与两侧巷道发生碰撞的情况。针对上述问题，提出了一种基于扩展卡尔曼滤波的多传感器融合清仓机器人位姿识别方法。首先搭建多传感器融合算法框架，建立里程计、惯性测量装置、激光雷达数据采集模型；其次基于扩展卡尔曼滤波原理，以惯性测量装置角度信息建立观测方程，结合里程计位姿信息，得到第1次融合的清仓机器人位姿矩阵，利用激光雷达的位置信息与之前的位姿矩阵进行迭代，得到第2次融合的清仓机器人位姿矩阵；最后采用互补滤波算法对融合后的清仓机器人位姿矩阵进行处理，输出最终的清仓机器人位姿矩阵。实验结果表明：在直线位姿识别中2次的最大位置误差为0.04 m，最大姿态角误差为0.05 rad；在模拟巷道实验中的最大位置误差为0.1 m，最大姿态角误差为0.085 rad；与AMCL方法相比，基于扩展卡尔曼滤波的清仓机器人位姿识别方法在减少清仓机器人运行过程中的累计误差方面表现出显著的有效性。Abstract: The lighting intensity of coal mine water storage roadways is uneven and the structured features are obvious. Traditional vision based robot pose recognition methods are not accurate. The single robot positioning techniques such as Adaptive Monte Carlo localization (AMCL) method have significant cumulative errors in the output pose information with the long-term operation of the cleaning robot. It is easy to encounter situations where the coal slurry is not cleaned thoroughly and collides with both sides of the roadway. In order to solve the above problem, a multi-sensor fusion clearance robot pose recognition method based on extended Kalman filtering is proposed. Firstly, the method builds a multi-sensor fusion algorithm framework and establishes models for odometer, inertial measurement devices, and LiDAR data acquisition. Secondly, based on the principle of extended Kalman filtering, an observation equation is established using the angle information of the inertial measurement device. Combined with the odometer pose information, the first fusion of the clearance robot pose matrix is obtained. Then, the position information of the lidar is iterated with the previous pose matrix to obtain the second fused clearance robot pose matrix. Finally, the complementary filtering algorithm is used to process the pose matrix of the clearance robot after two fusion and output the final pose matrix of the clearance robot. The experimental results show that the maximum position error in linear pose recognition is 0.04 m, and the maximum attitude angle error is 0.05 rad. The maximum position error in the simulated roadway experiment is 0.1 m, and the maximum attitude angle error is 0.085 rad. Compared with the AMCL method, the pose recognition method of the warehouse cleaning robot based on extended Kalman filtering shows significant effectiveness in reducing the cumulative error during the operation of the warehouse cleaning robot.
-
0. 引言
根据国家统计局2022 年数据显示，煤炭在我国能源结构中占比为56%，是我国能源体系中的主要供应来源[1]。在煤炭开采过程中，水害被列为五大灾害之一[2]。水仓是防止水害事故发生的重要措施，水仓沉积物的累积会降低水仓容积，使水仓失去蓄水作用，提高水害发生风险。《煤矿安全规程》规定：每年雨季前必须清理一次水仓。
目前常见的清仓方式主要有人工清仓、水力清仓、机械清挖等。人工清仓是目前主流的清仓方式[3]，需10～12名清仓工人连续清理2～3个月才能完成，清仓效率低且存在冲仓、漫仓等风险。水力清仓是利用高压水枪不断冲击煤泥淤积层，将煤泥进行稀释后通过排水泵排出，这种清仓方式在一定程度上降低了工人劳动强度，操作简单，但需在煤泥清理过程中注入大量水，进一步增加了水害发生的风险。机械清挖是通过装载机、挖掘机等设备将煤泥装入矿车，或采用压滤工艺将煤泥脱水后通过带式输送机运输，这种清仓方式清理效率高，但在清理过程中使用了大量设备，极大占用巷道工作空间，易对煤矿正常开采造成影响。因此，设计一种体积小、自动化程度高的煤矿水仓清理机器人势在必行。随着国家“机械化换人、自动化减人、安全至上”战略的提出，越来越多学者投入到清仓机器人研发过程中。郭培红等[4]设计了一种煤泥清挖泵送一体的清仓机，实现了水仓煤泥清理机械化，但在使用过程中需不断铺设管道，管道拆装成本高。宋峰等[5]设计了一款集煤泥清理、输送为一体的清仓机器人组，将清仓机定点安置在水仓口，通过装载机对煤泥进行转运，无需在水仓中铺设管道，降低了清仓成本，但整套系统体积庞大，易对煤矿正常开采造成影响。 姚贵英等[6]提出了一种可自行行走的水仓清理机器人，实现了对煤泥水的自主筛分、脱水，但整机自动化程度低。以上研究主要针对清仓机器人机械结构方面，清仓机器人在工作过程中仍需要依靠工人跟机操作，无法实现对煤泥的自主清理。
机器人位姿识别是实现清仓机器人自主清理煤泥的前提。目前位姿识别方法大多基于视觉识别：姚立健等[7]提出了一种基于改进型广义Hough变换的位姿检测方法，通过“形状相似度”法缩小检测范围，提高检测效率，但扩大了小目标物体的垂直视差；陈东旭等[8]针对焊接机器人位姿识别问题，提出了一种基于线结构光的位姿识别方法，结合图像处理工具获得位姿信息，这种方法位姿识别精度高，但适用范围有限，无法对复杂曲面进行有效检测；马斌等[9]采用单目视觉技术实现对钻杆的位姿识别， 提高了钻杆装卸自动化水平，但单目视觉容易出现图形畸变，导致偏差范围增加。由于水仓巷道中光照强度不均匀，视觉环境受光源布置影响较大，所以基于视觉的位姿识别方法在大多数情况下无法满足清仓机器人的使用要求。
机器人定位技术是提高清仓机器人位姿识别精度的关键技术。目前常见的机器人定位方法主要包括GPS定位、地磁定位、无限载波通信定位等。井下处于高岩土覆盖层，无法接收GPS信号 [10-11]。地磁定位对外界磁场要求较高，由于井下电磁设备对磁场干扰较大，无法满足机器人定位精度需求[12]。无线载波通信抗干扰能力强、灵活性高，适用于大多数场景的机器人定位[13]，但在使用过程中需提前布置无线网络，成本较高。
受井下复杂环境的影响，传统定位方法无法使用，通过传感器对井下环境识别并进行同步定位与建图（Simultaneous Localization and Mapping，SLAM）是解决井下定位困难问题的有效手段[14]。D. Fox等[15]首先将粒子滤波应用于机器人定位中，提出自适应蒙特卡罗定位（Adaptive Monte Carlo Localization，AMCL）方法，该方法在机器人定位过程中对采样粒子依赖严重，当采样粒子出现退化时，机器人本体姿态会出现无法弥补的误差，鲁棒性差。王宁等[16]利用重采样与相对熵交替采样对AMCL进行改进，有效降低了粒子退化，但无法消除机器人长期运行过程中产生的累计误差。冯佳萌等[17]通过增加扫描匹配和傅里叶滤波来优化AMCL算法，提高了算法的定位精度和鲁棒性，算法粒子退化现象得到了缓解，但该方法只适用于初始位姿精确的模型，对于初始位姿信息缺失的机器人定位易出现无法收敛的情况。
为了提高清仓机器人位姿识别的准确性和减少累计误差，本文提出了一种基于扩展卡尔曼滤波（Extended Kalman Filter，EKF）的多传感器融合的清仓机器人位姿识别方法。首先选择里程计、惯性测量装置和激光雷达作为数据来源，搭建位姿识别系统框架，设计传感器布置方式并建立传感器观测模型，然后综合考虑不同传感器性质建立观测方程，基于EKF算法对里程计、惯性测量装置、激光雷达数据进行2次融合，最后结合2次融合的位姿信息，通过互补滤波的方式得到清仓机器人高精度位姿。
1. 清仓机器人位姿识别系统结构
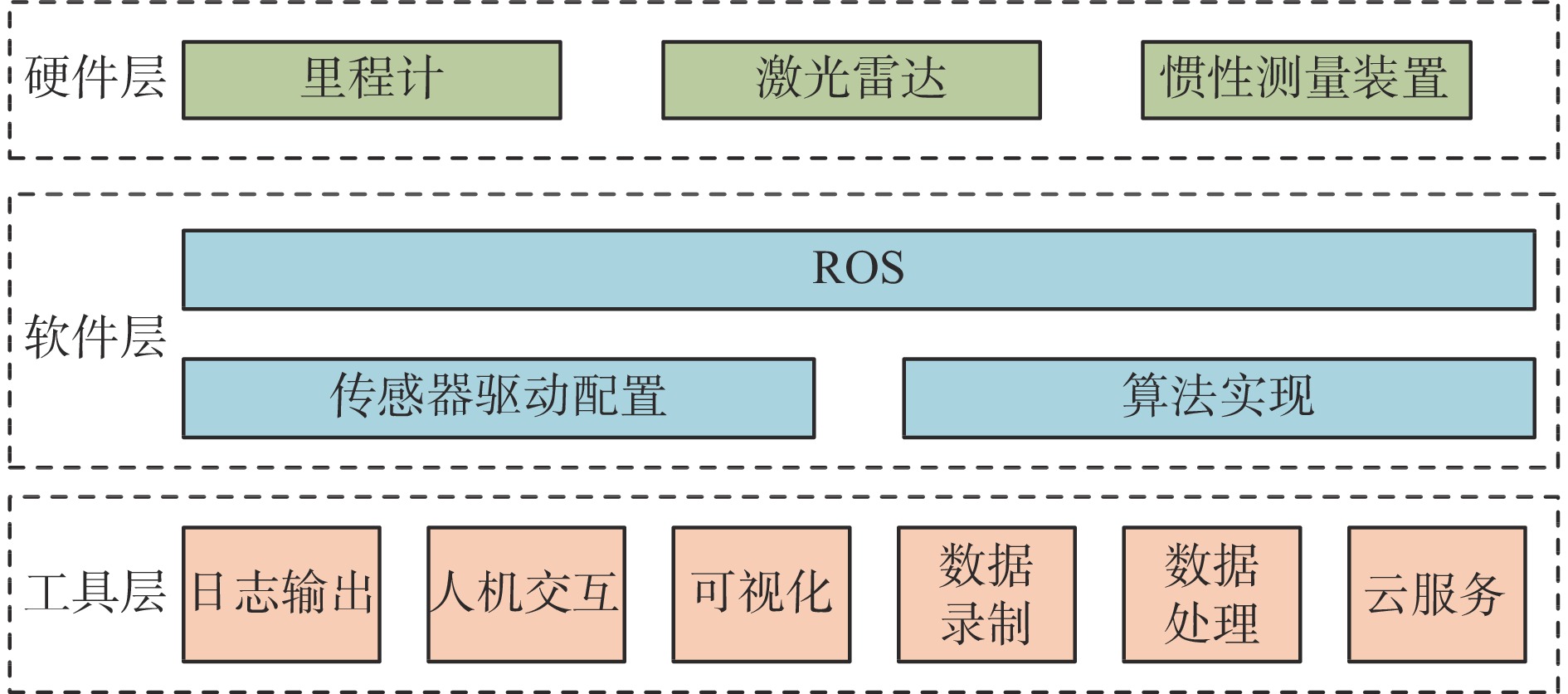
清仓机器人在清理煤泥过程中，需对所处环境及本身位姿进行识别，其位姿识别系统由硬件层、软件层和工具层组成，如图1 所示。硬件层是机器人的眼睛，包括里程计、激光雷达和惯性测量装置3个部分，负责数据采集。软件层是位姿识别系统的核心，基于机器人操作系统（Robot Operating System，ROS）对传感器驱动进行配置并实现位姿识别算法。工具层用于显示定位结果、测算定位精度等，包括日志输出、人机交互、可视化、数据录制、数据处理等工具。
![]()
图 1 清仓机器人位姿识别系统结构Figure 1. Structure of pose recognition system for warehouse clearance robot2. 传感器数据采集
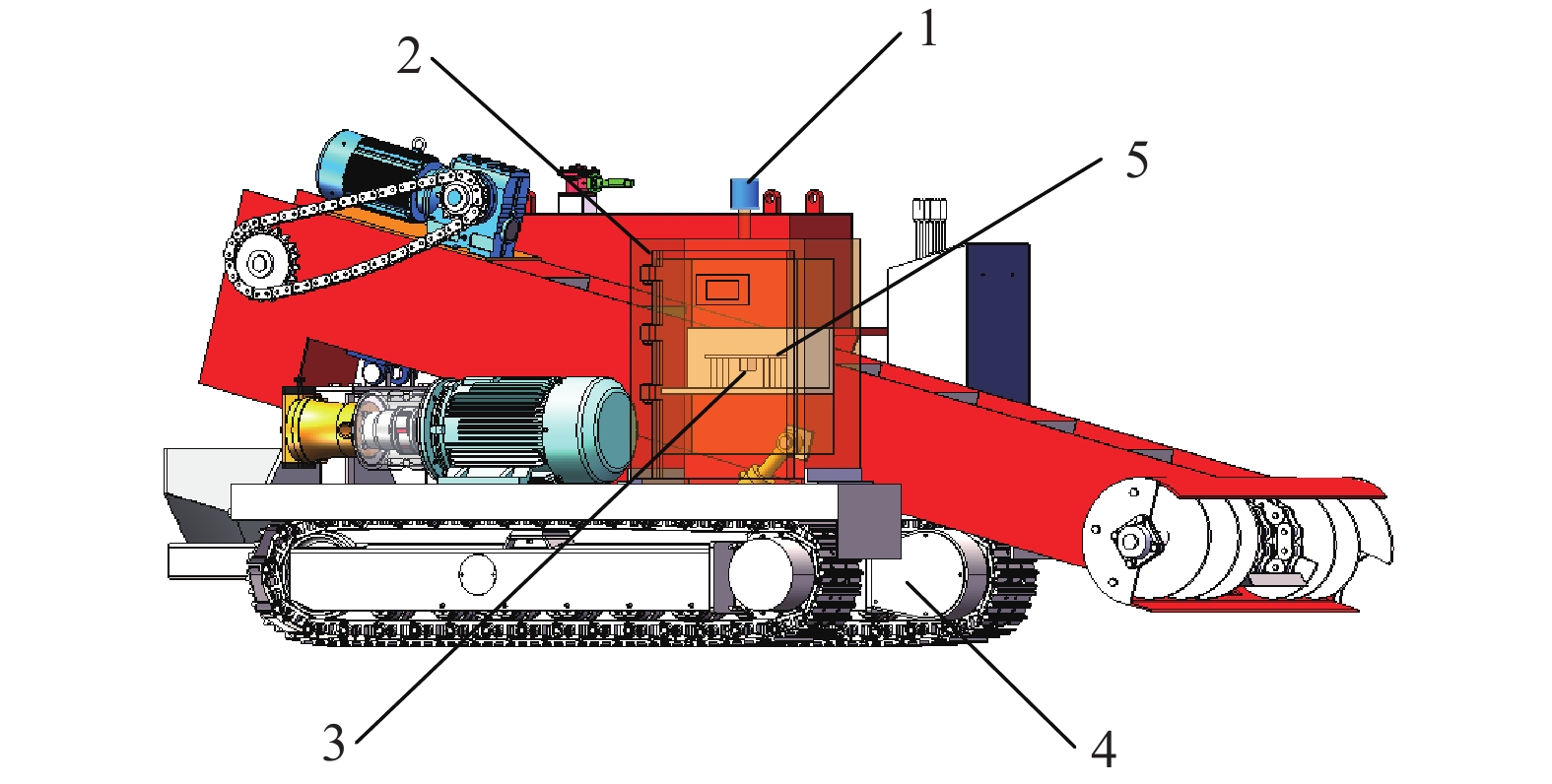
清仓机器人上的传感器布置如图2所示，将激光雷达安装在清仓机器人算法控制箱上方，采集激光点云数据；在履带两侧马达处分别安装2个里程计，收集清仓机器人行走过程中的速度、姿态数据；惯性测量装置安装在算法控制箱中，负责测量清仓机器人运行过程中的加速度、角速度数据；控制主板处理激光点云数据、里程计数据和惯性测量数据，得到清仓机器人位姿信息，控制清仓机器人对水仓进行清理。在清仓机器人位姿识别过程中选择惯性测量装置安装平面中心点作为衡量位姿变化的观测点。
![]()
图 2 清仓机器人上的传感器布置1−激光雷达 ；2−算法控制箱； 3−惯性测量装置；4−里程计； 5−控制主板。Figure 2. Sensor layout of warehouse cleaning robot2.1 里程计数据采集
里程计采样频率较高且在短时间内具有较高的定位精度，是机器人定位常用的传感器之一。里程计通过检测霍尔编码器高低电平的个数计算里程计运动圈数，从而判断机器人的位移，并结合左右两侧履带移动距离差推算机器人位姿变化值[18]。
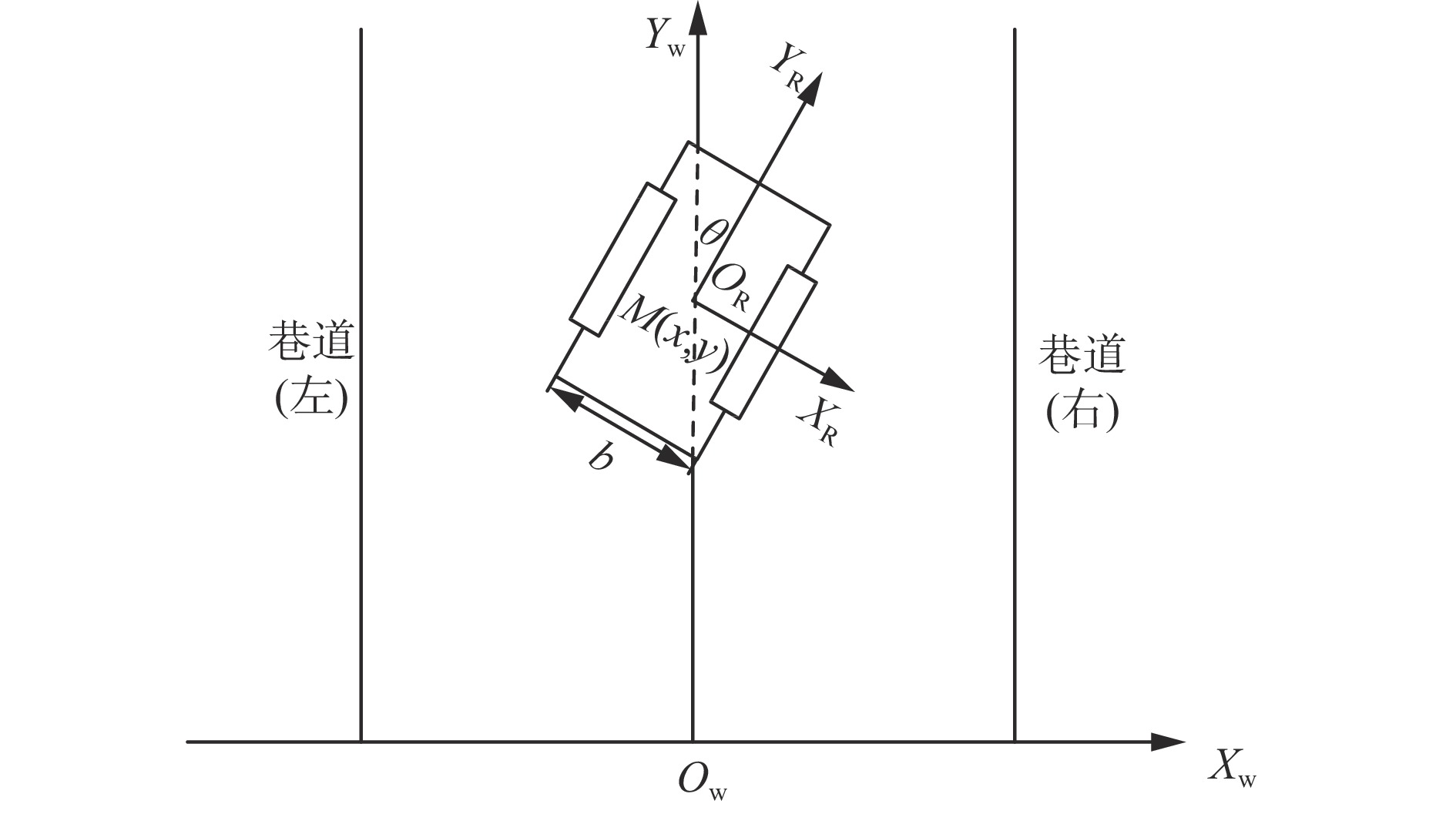
清仓机器人里程计运动模型如图3所示，将机器人看作巷道平面内运动的一个刚体[19]，以巷道一端中心点为原点，建立全局坐标系$ {X}_{{\mathrm{w}}}{Y}_{{\mathrm{w}}}{O}_{{\mathrm{w}}} $；以机器人质心M为原点，建立本体坐标系$ {X}_{{\mathrm{R}}}{Y}_{{\mathrm{R}}}{O}_{{\mathrm{R}}} $，2个坐标系夹角$ \theta $为姿态角，将机器人位姿信息写成$ 1\times 3 $矩阵。
t时刻机器人在M点处的速度为
$$ v\left(t\right)=\frac{{v}_{{\mathrm{L}}}+{v}_{{\mathrm{R}}}}{2} $$ (1) $$ \omega \left(t\right)=\frac{{v}_{{\mathrm{L}}}-{v}_{{\mathrm{R}}}}{b}$$ (2) 式中： $ v\left(t\right) $为机器人在M点的线速度；$ {v}_{{\mathrm{L}}},{v}_{{\mathrm{R}}} $分别为左、右轮线速度，通过霍尔编码器测量； $ \omega \left(t\right) $为机器人在M点的角速度；$ b $为机器人宽度。
里程计输出的机器人位姿为
$${\boldsymbol{q}}^{{\mathrm{od}}}={\int }_{0}^{t}\left[ \begin{array}{ccc}\cos\;\theta & -\sin\;\theta & 0\\ \sin\;\theta & \cos\;\theta & 0\\ 0& 0& 1\end{array} \right]\left[ \begin{array}{c}v\left(t\right)\\ 0\\ \omega \left(t\right)\end{array} \right]{\mathrm{d}}t+{{{\boldsymbol{\varepsilon}} }}_{{\mathrm{od}}}$$ (3) 式中：$ {\boldsymbol{q}}^{{\mathrm{od}}} $为里程计输出的位姿矩阵；$ {\boldsymbol{\varepsilon }}_{{\mathrm{od}}} $为里程计误差。
2.2 惯性测量装置数据采集
惯性测量装置主要通过加速度计和陀螺仪获得清仓机器人的加速度、角速度信息，通过对加速度的2次积分获得清仓机器人的位置信息[20]，采用方向余弦矩阵对姿态角信息进行解算。
对加速度进行第1次积分得到清仓机器人运行速度信息。
$$ \left[ \begin{array}{c}{v}_{x}\\ {v}_{y}\\ {v}_{{\textit{z}}}\end{array} \right]=\int \left[ \begin{array}{c}{{a}}_{{x}}\\ {{a}}_{{y}}\\ {{a}}_{{\textit{z}}}\end{array} \right]\mathrm{d}t $$ (4) 式中：$ {v}_{x},{v}_{y},{v}_{{\textit{z}}} $分别为清仓机器人在x，y，z方向速度；$ {a}_{x},{a}_{y},{a}_{{\textit{z}}} $分别为清仓机器人绕x，y，z轴的加速度，可通过加速度计测量得到。
由于清仓机器人在巷道平面内运动，在z方向上速度为0，只需对x，y方向上的速度进行第2次积分，即可得到机器人位置信息。
$$ \left[ \begin{array}{c}{x}^{{\mathrm{imu}}}\\ {y}^{{\mathrm{imu}}}\end{array} \right]=\int \left[ \begin{array}{c}{v}_{x}\\ {v}_{y}\end{array} \right]\mathrm{d}t$$ (5) 式中$ {x}^{{\mathrm{imu}}},{y}^{{\mathrm{imu}}} $为惯性测量装置输出的位置信息。
采用方向余弦矩阵对姿态角信息进行解算，将清仓机器人看成对坐标轴的旋转，对方向余弦矩阵求导得到姿态角导数的微分方程。
$$ \left\{ \begin{array}{l}\dot{\alpha }=\left({\omega }_{y}\;\sin\;\alpha +{\omega }_{{\textit{z}}}\;\sin\;\alpha \right)\tan\;\beta +{\omega }_{x}\\ \dot{\beta }={\omega }_{y}\;\cos\;\alpha -{\omega }_{{\textit{z}}}\;\sin\;\alpha \\ \dot{\gamma }=\dfrac{{\omega }_{y}\;\sin\;\alpha +{\omega }_{{\textit{z}}}\;\sin\;\alpha }{\cos\;\beta }\end{array}\right. $$ (6) 式中： $ \dot{\alpha },\dot{\beta },\dot{\gamma } $为姿态角的导数；$ {\omega }_{x},{\omega }_{y},{\omega }_{{\textit{z}}} $分别为清仓机器人绕x，y，z轴的角速度，可通过陀螺仪测量得到；$ \alpha ,\beta ,\gamma $分别为清仓机器人绕x，y，z轴旋转的姿态角。
清仓机器人初始姿态角${\alpha }_{0},{\beta }_{0},{\gamma }_{0} $为
$$ \left\{ \begin{array}{l}\alpha_0=\mathrm{arcsin}\dfrac{a_y}{\mathit{\mathrm{\mathit{g}}}} \\ \beta_0=\mathrm{arcsin}\dfrac{a_x}{\mathrm{\mathit{g}}} \\ \gamma_0=0\end{array}\right. $$ (7) 式中$ {g} $为重力加速度。
根据清仓机器人初始姿态角，采用龙格库塔法对微分方程进行求解，得到清仓机器人的姿态角。
选取清仓机器人在x，y方向上的位置数据和绕z轴旋转角$ \gamma $作为姿态数据，建立位姿矩阵，惯性测量装置输出的机器人位姿为
$$ {\boldsymbol{q}}^{{\mathrm{imu}}}=\left[ \begin{array}{c}{x}^{{\mathrm{imu}}}\\ {y}^{{\mathrm{imu}}}\\ \gamma \end{array} \right]+{\boldsymbol{\varepsilon }}_{{\mathrm{imu}}} $$ (8) 式中：$ {\boldsymbol{q}}^{{\mathrm{imu}}} $为惯性测量装置输出的位姿矩阵； $ {\boldsymbol{\varepsilon }}_{{\mathrm{imu}}} $为惯性测量误差。
2.3 激光雷达数据采集
激光雷达通过发射激光束并收集返回数据获取环境中物体的位置信息，实现高精度环境地图的构建，为机器人提供精确、可靠的位置信息，在机器人位姿识别过程中起着重要的作用[21]。激光雷达输出值为极坐标系下激光雷达障碍物距离与角度信息。
$$ {{L}}_{{\mathrm{laser}}}=\left\{\left({l}_{i},{\varphi }_{i}\right),i=\mathrm{1,2},\cdots \right\}$$ (9) 式中：$ {l}_{i} $ 为激光雷达与障碍物距离； $ {\varphi }_{i} $ 为激光雷达与障碍物的偏转角度，即测量姿态角。
将$ {{L}}_{{\mathrm{laser}}} $转换至直角坐标系：
$$\left\{ \begin{array}{l}{x}^{{\mathrm{laser}}}=l_i\;\mathrm{cos}\;\varphi_i \\ {y}^{{\mathrm{laser}}}=l_i\;\mathrm{sin}\;\varphi_i \end{array}\right. $$ (10) 式中$ {x}^{{\mathrm{laser}}},{y}^{{\mathrm{laser}}} $分别为激光雷达输出的直角坐标系下坐标。
激光雷达输出的机器人位姿为
$$ {\boldsymbol{q}}^{{\mathrm{laser}}}=\left[ \begin{array}{c}{x}^{{\mathrm{laser}}}\\ {y}^{{\mathrm{laser}}}\\ \varphi_i \end{array} \right]+{\boldsymbol{\varepsilon }}_{{\mathrm{laser}}} $$ (11) 式中：$ {\boldsymbol{q}}^{{\mathrm{laser}}} $为激光雷达输出的位姿矩阵； $ {\boldsymbol{\varepsilon }}_{{\mathrm{laser}}} $为激光雷达测量误差。
3. 多传感器融合机器人位姿识别方法
3.1 AMCL算法
AMCL算法将机器人位姿看成粒子在地图上的概率分布，利用里程计运动模型和激光雷达数据获取清仓机器人在已知地图环境下的位姿信息[22]。
在实际应用中，首先对AMCL系统进行初始化，设置粒子滤波器的状态及粒子权重，利用里程计得到机器人初始位姿信息，使用里程计数据更新粒子滤波器状态，然后通过激光雷达数据与环境地图信息进行对比，更新粒子滤波器中粒子权重，最后根据粒子权重进行重采样，使用高权重粒子替代低权重粒子，得到机器人位姿信息。
3.2 基于EKF的多传感器融合定位算法
由于AMCL在粒子采集过程中选用正态分布假设，易导致采集粒子出现偏差，这种偏差在短时间内对位姿影响不大，但随着清仓机器人长时间运行，这种偏差会逐渐累加，导致定位精度差，甚至是无法定位。针对上述问题，本文基于EKF[23]提出一种多传感器融合的位姿识别方法，以解决粒子滤波中粒子采集偏差问题，实现清仓机器人在长时间运行中对位姿的高精度识别。
3.2.1 EKF基本原理
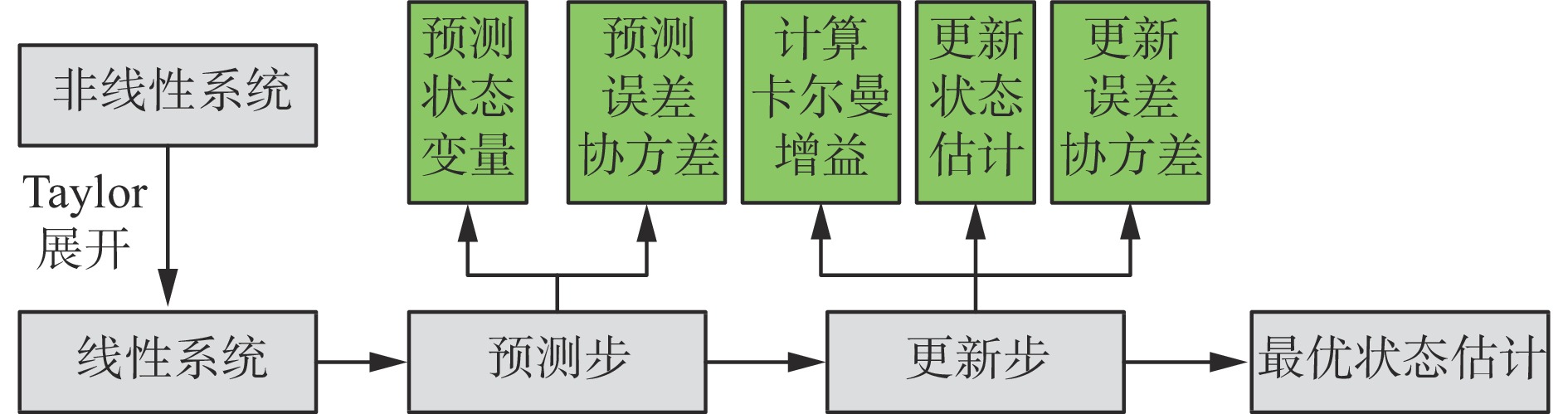
EKF基本原理如图4所示，首先将非线性系统通过Taylor公式得到近似线性化系统，其次通过预测步建立预测状态方程并计算预测误差协方差矩阵，然后通过更新步计算卡尔曼增益，并更新后验状态矩阵和后验误差协方差矩阵，最后得到系统最优状态估计。
3.2.2 多传感器融合算法设计
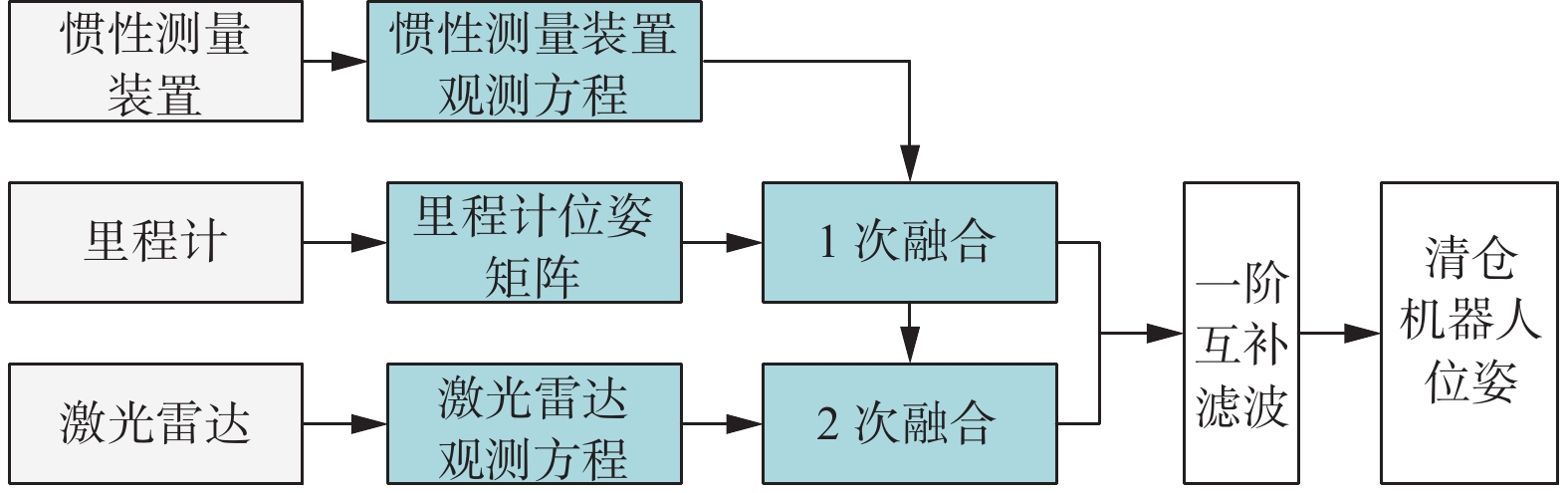
多传感器融合算法原理如图5所示，基于EKF原理，对里程计、惯性测量装置、激光雷达数据进行2次融合，然后通过一阶互补滤波结合融合后的数据得到清仓机器人的位姿矩阵。
具体步骤如下：
1） 对里程计数据和惯性测量数据进行处理，减小里程计打滑引起的误差；根据EKF基本原理，得到里程计系统状态函数。
$$ {\boldsymbol{q}}_{t+1}={\boldsymbol{Aq}}_{t}^{{\mathrm{od}}}+{\boldsymbol{Bu}}_{t} $$ (12) 式中：$ {\boldsymbol{q}}_{t+1} $为$ t+1 $时刻清仓机器人状态矩阵；$ \boldsymbol{A} $为系统状态矩阵，将里程计数据转换成清仓机器人位姿信息；$ {\boldsymbol{q}}_{t}^{{\mathrm{od}}} $为$ t $ 时刻清仓机器人状态矩阵；B为控制变量矩阵，将系统控制向量转换成位姿信息； $ {\boldsymbol{u}}_{t} $为系统控制向量，包括$ t $时刻里程计输出的线速度、角速度等。
采用惯性测量装置采集的数据作为观测数据，建立观测方程：
$$ {\boldsymbol{H}}_{t}^{{\mathrm{imu}}}={\boldsymbol{h}}^{{\mathrm{imu}}}\left[ \begin{array}{c}{x}^{{\mathrm{imu}}}\\ {y}^{{\mathrm{imu}}}\\ \gamma \end{array} \right]+{\boldsymbol{\varepsilon }}_{{\mathrm{imu}}} $$ (13) 式中$ {\boldsymbol{h}}^{{\mathrm{imu}}} $为惯性测量装置观测矩阵。
$$ {\boldsymbol{h}}^{{\mathrm{imu}}}=\left[ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array} \right]$$ (14) 对里程计数据和惯性测量装置数据进行融合：
$$ {\boldsymbol{q}}_{{\mathrm{out1}}}={\boldsymbol{q}}_{t+1}+{\boldsymbol{K}}_{t+1}^{{\mathrm{Io}}}{\boldsymbol{\varepsilon }}_{{\mathrm{imu}}}$$ (15) 式中$ {\boldsymbol{K}}_{t+1}^{{\mathrm{Io}}} $为第1次融合后的卡尔曼增益。
$${\boldsymbol{K}}_{t+1}^{{\mathrm{Io}}}={\boldsymbol{\varepsilon }}_{{\mathrm{od}}}{[{\boldsymbol{h}}^{{\mathrm{imu}}}{\boldsymbol{\varepsilon }}_{{\mathrm{od}}}{({\boldsymbol{h}}^{{\mathrm{imu}}})}^{{\mathrm{T}}}+{\boldsymbol{\varepsilon }}_{{\mathrm{imu}}}]}^{-1} $$ (16) 此时系统误差矩阵为
$$ {\boldsymbol{\varepsilon }}_{{\mathrm{IO}}}=[\boldsymbol{I}-{\boldsymbol{K}}_{t+1}^{{\mathrm{Io}}}{\boldsymbol{h}}^{{\mathrm{imu}}}]{\boldsymbol{\varepsilon }}_{{\mathrm{imu}}} $$ (17) 式中$ \boldsymbol{I} $为单位矩阵。
2） 将里程计与惯性测量装置融合后的数据作为清仓机器人的状态信息，建立激光雷达观测方程：
$$ {\boldsymbol{H}}_{t}^{{\mathrm{laser}}}={\boldsymbol{h}}^{{\mathrm{laser}}}\left[ \begin{array}{c}{x}^{{\mathrm{laser}}}\\ {y}^{{\mathrm{laser}}}\\ \varphi \end{array} \right]+{\boldsymbol{\varepsilon }}_{{\mathrm{laser}}} $$ (18) 式中$ {\boldsymbol{h}}^{{\mathrm{laser}}} $为激光雷达观测矩阵。
$$ {\boldsymbol{h}}^{{\mathrm{laser}}}=\left[ \begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\end{array} \right]$$ (19) 融合激光雷达后的位姿为
$$ {\boldsymbol{q}}_{{\mathrm{out2}}}={\boldsymbol{q}}_{{\mathrm{out1}}}+{\boldsymbol{K}}_{t+1}{\boldsymbol{\varepsilon }}_{{\mathrm{laser}}} $$ (20) 式中$ {\boldsymbol{K}}_{t+1} $为第2次融合后的卡尔曼增益。
$$ {\boldsymbol{K}}_{t+1}={\boldsymbol{\varepsilon }}_{{\mathrm{IO}}}{\left[{\boldsymbol{\varepsilon }}_{{\mathrm{IO}}}+{\boldsymbol{\varepsilon }}_{{\mathrm{laser}}}\right]}^{-1} $$ (21) 3） 对2次融合后输出的位姿信息进行互补滤波，得到清仓机器人位姿。
$${\boldsymbol{q}}={\sigma }_{1}{\boldsymbol{q}}_{{\mathrm{out1}}}+{\sigma }_{2}{\boldsymbol{q}}_{{\mathrm{out2}}}$$ (22) 式中$ {\sigma }_{1},{\sigma }_{2} $分别为第1次融合和第2次融合的权重因子，由于第2次融合得到的位姿信息中包含有第1次融合信息，且激光雷达测距精度高，取$ {\sigma }_{1}=0.2 $，$ {\sigma }_{2}=0.8 $。
4. 实验研究
4.1 实验平台搭建
实验系统选择Ubuntu18.04长期支持版，ROS版本选择Melodic，上位机采用VirtualBox烧录Ubuntu18.04系统安装ROS-Noetic长期支持版，机器人由小车底盘、激光雷达及惯性测量装置等组成。激光雷达频率为5 Hz，惯性测量装置频率为100 Hz，里程计采用霍尔编码器，实验平台如图6所示。
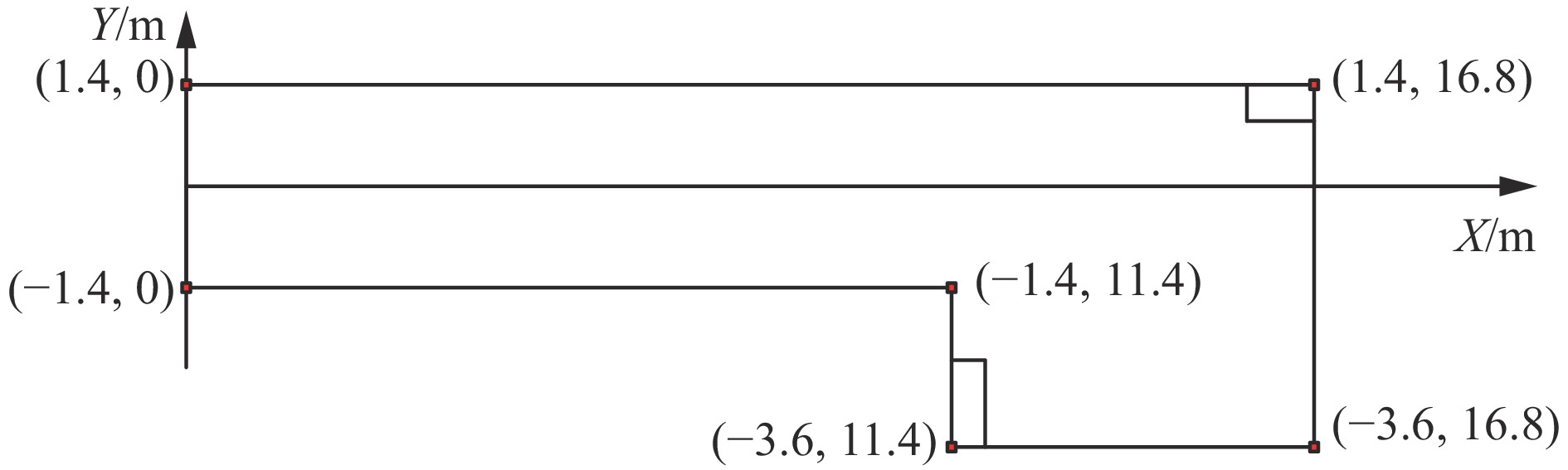
选用长为16.8 m、最大宽度为5 m、最小宽度为2.8 m的实验环境模拟井下巷道环境，在灯光昏暗的条件下进行清仓机器人位姿识别实验，环境平面图如图7所示。
4.2 机器人位姿识别实验
将树莓派与上位机连接在同一局域网，上位机通过远程登录服务连接树莓派并通过本机远程桌面进行登录。在Rviz中分别订阅Map，Pose-array，Path，Odom，Scan等相关节点对机器人上的传感器数据进行可视化显示。实验主要包括沿直线方向位姿识别精度测试和沿模拟巷道位姿识别精度测试。
基于Gmapping算法[24]构建全局一致性地图（图8），红色坐标轴为x轴，绿色坐标轴为y轴；黑色轮廓线为定位前建立的静态地图，青色包裹层区为膨胀层，其目的是防止机器人与两侧巷道发生碰撞。
4.2.1 沿直线位姿识别精度测试
为测试实验小车硬件系统的可靠性和位姿识别算法的稳定性，选择在x方向上进行位姿识别精度测试（图9），控制机器人沿x轴行走10 m并返回。由图9（a）可看出，在机器人运行到10 m位置时，AMCL定位结果为10.132 6 m，本文方法定位结果为10.045 2 m；由图9（b）可看出，AMCL在y方向上的最大定位误差为0.17 m，平均位置误差为0.08 m，本文方法可将位置误差控制在0.04 m之内；由图9（c）可看出，采用AMCL获得的最大姿态角误差为0.15 rad，平均姿态角误差为0. 08 rad，采用本文方法获得最大姿态角误差为 0.05 rad，平均姿态角误差为0.03 rad。
4.2.2 模拟巷道位姿识别精度测试
为模拟清仓机器人实际运行过程中可能遇到的各种情况，提高位姿识别算法的有效性和实用性，在模拟巷道中进行位姿识别精度测试。
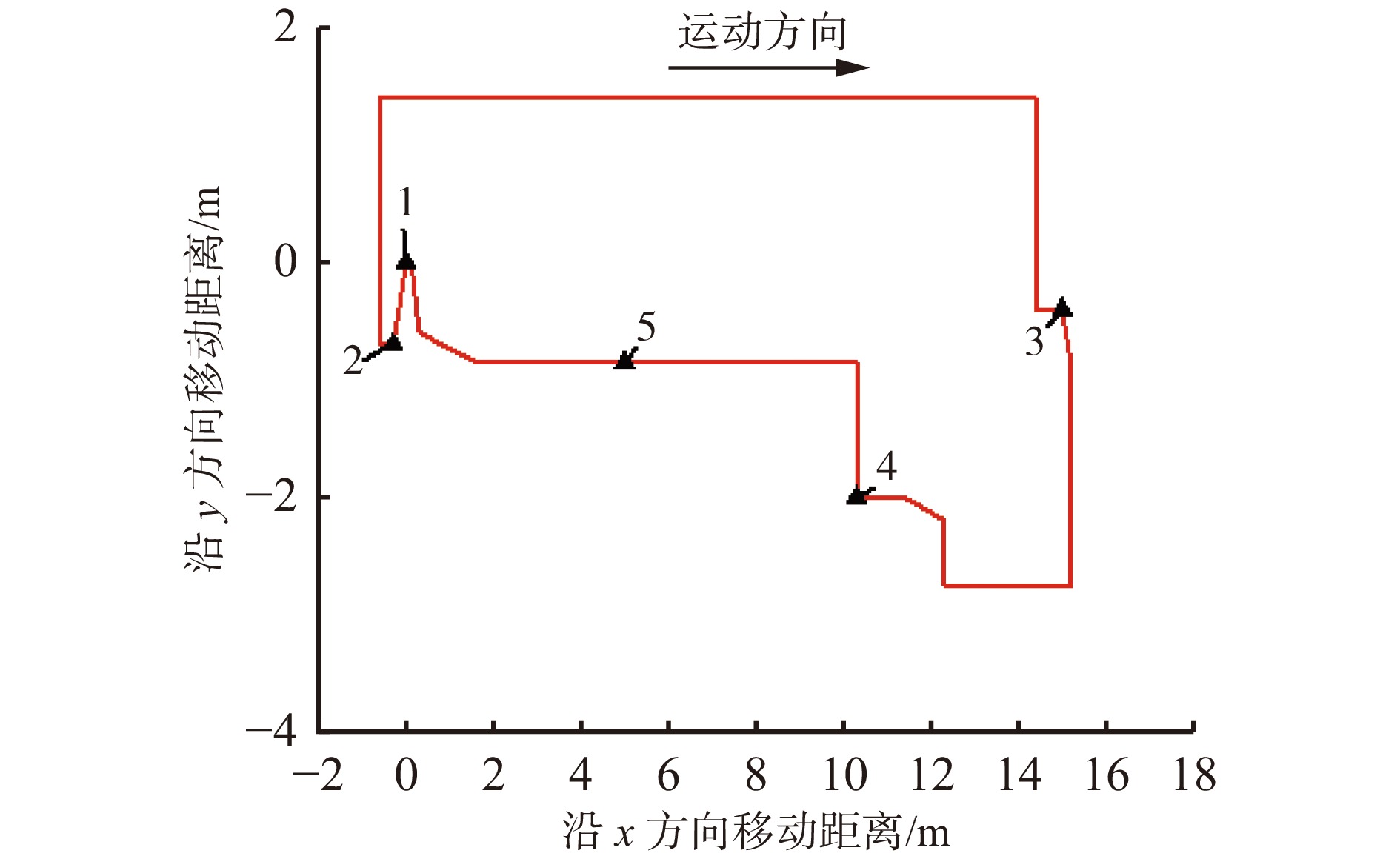
在模拟巷道进行轨迹预设，如图10所示。通过上位机键盘控制节点来控制清仓机器人沿着预设轨迹运动，在模拟巷道中选取5个观测点对位姿识别结果进行定量分析，结果见表1、表2。
位置误差采用欧氏距离公式计算，姿态角误差用真实姿态角与测量姿态角差的绝对值表示。
表 1 坐标点实际值与2种方法处理结果Table 1. Actual values of coordinate points and processing results using two methodsm 观测点编号 真实坐标 测量坐标 AMCL 本文方法 1 （0.0, 0.0） （−0.04, −0.03） （−0.015, −0.003） 2 （−0.3, − 0.7） （−0.326, −0.796） （−0.316, −0.726） 3 （15, −0.4） （15.105, −0.427） （15.034, −0.423） 4 （10.3, −2） （10.435, −1.877） （10.289, −1.893） 5 （5, −0.85） （5.105, −0.691） （5.043, −0.821） 表 2 姿态角实际值与2种方法处理结果Table 2. Actual value of attitude angle and processing results using two methodsrad 观测点编号 真实姿态角 测量姿态角 AMCL 本文方法 1 1.45 1.428 1.463 2 −3.14 −3.054 −3.123 3 0.15 0.052 0.093 4 1.57 1.421 1.485 5 3.14 2.975 3.085 $$ d=\sqrt{{\left({x}_{i}-x\right)}^{2}+{\left({y}_{i}-y\right)}^{2}} $$ (23) $$\varDelta =\left|{\varphi }_{i}-\varphi \right| $$ (24) 式中：d 为位置误差；（$ {x}_{i}，{y}_{i} $）为测量坐标；（x，y）为 真实坐标；$ {\varDelta } $ 为角度误差； $ \varphi $ 为真实姿态角。
位置误差和姿态角误差对比分析见表3，可看出AMCL定位的最大位置误差为0.19 m，最大姿态角误差为0.165 rad，平均位置误差为0.126 m，平均姿态角误差为0.104 rad；本文方法的最大位置误差为0.1 m，最大姿态角误差为0.085 rad，平均位置误差为0.049 m，平均姿态角误差为0.045 rad。说明多传感器融合与位姿优化方法能有效提高清仓机器人位姿识别精度。
表 3 位置误差和姿态角误差对比分析Table 3. Comparative analysis of pose error and attitude angle error编号 位置误差/m 姿态角误差/rad AMCL 本文方法 AMCL 本文方法 1 0.05 0.02 0.022 0.013 2 0.10 0.03 0.086 0.017 3 0.11 0.04 0.098 0.057 4 0.18 0.10 0.149 0.085 5 0.19 0.05 0.165 0.055 5. 结论
1） 搭建位姿识别算法框架，建立里程计、惯性测量装置、激光雷达数据采集模型，基于EKF对传感器数据进行2 次融合，通过一阶互补滤波算法对2 次融合的位姿结果进行处理，得到高精度清仓机器人位姿。
2） 沿直线位姿识别精度的实验结果表明，多传感器融合与位姿优化的方法在清仓机器人直线行走中可将位置误差控制在0.04 m之内，将姿态角误差控制在0.05 rad之内。
3） 模拟巷道位姿识别精度的实验结果表明，多传感器融合与位姿优化的方法在模拟巷道实验中，平均位置误差为0.049 m，平均姿态角误差为0.045 rad。
-
![]()
图 1 清仓机器人位姿识别系统结构
Figure 1. Structure of pose recognition system for warehouse clearance robot
![]()
图 2 清仓机器人上的传感器布置
1−激光雷达 ；2−算法控制箱； 3−惯性测量装置；4−里程计； 5−控制主板。
Figure 2. Sensor layout of warehouse cleaning robot
表 1 坐标点实际值与2种方法处理结果
Table 1 Actual values of coordinate points and processing results using two methods
m 观测点编号 真实坐标 测量坐标 AMCL 本文方法 1 （0.0, 0.0） （−0.04, −0.03） （−0.015, −0.003） 2 （−0.3, − 0.7） （−0.326, −0.796） （−0.316, −0.726） 3 （15, −0.4） （15.105, −0.427） （15.034, −0.423） 4 （10.3, −2） （10.435, −1.877） （10.289, −1.893） 5 （5, −0.85） （5.105, −0.691） （5.043, −0.821） 
下载: 导出CSV
表 2 姿态角实际值与2种方法处理结果
Table 2 Actual value of attitude angle and processing results using two methods
rad 观测点编号 真实姿态角 测量姿态角 AMCL 本文方法 1 1.45 1.428 1.463 2 −3.14 −3.054 −3.123 3 0.15 0.052 0.093 4 1.57 1.421 1.485 5 3.14 2.975 3.085
下载: 导出CSV
表 3 位置误差和姿态角误差对比分析
Table 3 Comparative analysis of pose error and attitude angle error
编号 位置误差/m 姿态角误差/rad AMCL 本文方法 AMCL 本文方法 1 0.05 0.02 0.022 0.013 2 0.10 0.03 0.086 0.017 3 0.11 0.04 0.098 0.057 4 0.18 0.10 0.149 0.085 5 0.19 0.05 0.165 0.055
下载: 导出CSV
-
[1] 贾建称,贾茜,桑向阳,等. 我国煤矿地质保障系统建设30年:回顾与展望[J]. 煤田地质与勘探,2023,51(1):86-106. JIA Jiancheng,JIA Qian,SANG Xiangyang,et al. Review and prospect of coal mine geological guarantee system in China during 30 years of construction[J]. Coal Geology & Exploration,2023,51(1):86-106.
[2] 曾一凡,武强,赵苏启,等. 我国煤矿水害事故特征、致因与防治对策[J]. 煤炭科学技术,2023,51(7):1-14. ZENG Yifan,WU Qiang,ZHAO Suqi,et al. Characteristics,causes,and prevention measures of coal mine water hazard accidents in China[J]. Coal Science and Technology,2023,51(7):1-14.
[3] 石军杰,高贵军,游青山,等. 煤矿井下水仓清理机器人系统设计与应用[J]. 煤炭工程,2022,54(11):205-208. SHI Junjie,GAO Guijun,YOU Qingshan,et al. Water bin cleaning robot system for underground coal mine[J]. Coal Engineering,2022,54(11):205-208.
[4] 郭培红,薛蛟生,朱建安,等. 全液压水仓煤泥清挖泵送一体机研制[J]. 煤矿机械,2015,36(1):148-150. GUO Peihong,XUE Jiaosheng,ZHU Jian'an,et al. Development of cleaning-pumping combined machine with full hydraulic control for coal slime in water sump[J]. Coal Mine Machinery,2015,36(1):148-150.
[5] 宋峰,蒲仁利,钟灵敏,等. 一种矿用水仓清淤系统:CN202210801796.5[P]. 2022-09-02. SONG Feng,PU Renli,ZHONG Lingmin,et al. A mine water bin dredging system:CN202210801796.5[P]. 2022-09-02.
[6] 姚贵英,曹梦媛,马婧. 煤矿水仓清理机器人研究与设计[J]. 煤矿机械,2020,41(2):4-6. YAO Guiying,CAO Mengyuan,MA Jing. Research and design of coal mine sump cleaning robot[J]. Coal Mine Machinery,2020,41(2):4-6.
[7] 姚立健,丁为民,张培培,等. 基于改进型广义Hough变换的茄子果实位姿识别方法[J]. 农业工程学报,2009,25(12):128-132. DOI: 10.3969/j.issn.1002-6819.2009.12.023 YAO Lijian,DING Weimin,ZHANG Peipei,et al. Recognition method of position and attitude of eggplant fruits based on improved generalized Hough transforms[J]. Transactions of the Chinese Society of Agricultural Engineering,2009,25(12):128-132. DOI: 10.3969/j.issn.1002-6819.2009.12.023
[8] 陈东旭,赵铁军,乔赫廷. 基于线结构光的焊缝位姿识别研究[J]. 机械工程与自动化,2021(4):38-40,43. CHEN Dongxu,ZHAO Tiejun,QIAO Heting. Research on weld position-posture recognition based on line structured light[J]. Mechanical Engineering & Automation,2021(4):38-40,43.
[9] 马斌,彭光宇. 基于单目视觉的钻杆位姿识别技术研究[J]. 煤田地质与勘探,2022,50(10):171-178. DOI: 10.12363/issn.1001-1986.22.01.0036 MA Bin,PENG Guangyu. Research on drill pipe pose recognition technology based on monocular vision[J]. Coal Geology & Exploration,2022,50(10):171-178. DOI: 10.12363/issn.1001-1986.22.01.0036
[10] KEDONG W. A new algorithm for fine acquisition of GPS carrier frequency[J]. GPS Solutions,2014,18(4):581-592. DOI: 10.1007/s10291-013-0356-2
[11] 黄西平,杨飞. 综采工作面巡检机器人自主定位方法[J]. 工矿自动化,2023,49(4):86-91. HUANG Xiping,YANG Fei. Autonomous positioning method for inspection robots in fully mechanized working face[J]. Journal of Mine Automation,2023,49(4):86-91.
[12] 陆一,魏东岩,纪新春,等. 地磁定位方法综述[J]. 导航定位与授时,2022,9(2):118-130. LU Yi,WEI Dongyan,JI Xinchun,et al. Review of geomagnetic positioning method[J]. Navigation Positioning and Timing,2022,9(2):118-130.
[13] 崔苗,喻鑫,李学易,等. 多载波无线携能通信的上下行链路联合资源分配[J]. 通信学报,2019,40(3):206-214. DOI: 10.11959/j.issn.1000-436x.2019052 CUI Miao,YU Xin,LI Xueyi,et al. Joint downlink and uplink resource allocation for multi-carrier SWIPT system[J]. Journal on Communications,2019,40(3):206-214. DOI: 10.11959/j.issn.1000-436x.2019052
[14] SMITH R,SELF M,CHEESEMAN P. Estimating uncertain spatial relationships in robotics[J]. Machine Intelligence & Pattern Recognition,1988,5(5):435-461.
[15] FOX D,BURGARD W,DELLAERT F,et al. Monte carlo localization:efficient position estimation for mobile robots[C]. Sixteenth National Conference on Artificial Intelligence,Orland,1999.
[16] 王宁,王坚,李丽华. 一种改进的AMCL机器人定位方法[J]. 导航定位学报,2019,7(3):31-37. WANG Ning,WANG Jian,LI Lihua. An improved adaptive monte carlo localization method for robot[J]. Journal of Navigation and Positioning,2019,7(3):31-37.
[17] 冯佳萌,裴东,邹勇,等. 基于机器人激光定位的一种改进AMCL算法[J]. 激光与光电子学进展,2021,58(20):479-487. FENG Jiameng,PEI Dong,ZOU Yong,et al. An improved AMCL algorithm based on robot laser localization[J]. Laser & Optoelectronics Progress,2021,58(20):479-487.
[18] 马先重. 基于多传感器融合的室内移动机器人定位及障碍物检测与测量研究[D]. 武汉:武汉科技大学,2021. MA Xianchong. Research on localization and obstacle detection and measurement of indoor mobile robot based on multi sensor fusion[D]. Wuhan:Wuhan University of Science and Technology,2021.
[19] 金书奎,寇子明,吴娟. 煤矿水泵房巡检机器人路径规划与跟踪算法的研究[J]. 煤炭科学技术,2022,50(5):253-262. JIN Shukui,KOU Ziming,WU Juan. Research on path planning and tracking algorithm of inspection robot in coal mine water[J]. Coal Science and Technology,2022,50(5):253-262.
[20] 宗意凯,苏淑靖,高瑜宏. 基于多源IMU和粒子滤波优化的姿态融合算法[J]. 仪表技术与传感器,2023(8):88-95. DOI: 10.3969/j.issn.1002-1841.2023.08.015 ZONG Yikai,SU Shujing,GAO Yuhong. Attitude fusion algorithm based on multi-source IMU and particle filter optimization[J]. Instrument Technique and Sensor,2023(8):88-95. DOI: 10.3969/j.issn.1002-1841.2023.08.015
[21] 沈斯杰,田昕,魏国亮,等. 基于2D激光雷达的SLAM算法研究综述[J]. 计算机技术与发展,2022,32(1):13-18,46. DOI: 10.3969/j.issn.1673-629X.2022.01.003 SHEN Sijie,TIAN Xin,WEI Guoliang,et al. Review of SLAM algorithm based on 2D lidar[J]. Computer Technology and Development,2022,32(1):13-18,46. DOI: 10.3969/j.issn.1673-629X.2022.01.003
[22] PENG Gang,ZHENG Wei,LU Zezao,et al. An improved AMCL algorithm based on laser scanning match in a complex and unstructured environment[J]. Complexity,2018(5):1-11.
[23] ARASARATNAM I,HAYKIN S,ELLIOTT R J. Discrete-time nonlinear filtering algorithms using gauss-hermite quadrature[J]. Proceedings of the IEEE,2007,95(5):953-977.
[24] SU Zhifeng,ZHOU Jiehua,DAI Jiyang,et al. Optimization design and experimental study of gmapping algorithm[C]. Chinese Control and Decision Conference,Hefei,2020. DOI: 10.1109/CCDC49329.2020.9164603.
-
期刊类型引用(1)
1. 问永忠，贾澎涛，夏敏高，张龙刚，王伟峰. 基于改进YOLOv8n的井下人员多目标检测. 工矿自动化. 2025(01): 31-37+77 . 
本站查看
其他类型引用(1)
计量
- 文章访问数: 102
- HTML全文浏览量: 31
- PDF下载量: 21
- 被引次数: 2
