0.   引言

煤矿救援机器人可在危险区域对环境进行探测，对矿工实施救援，对于提高煤矿灾后救援效率、减少二次伤亡具有重要意义^[1]。路径规划是煤矿救援机器人研究的重要内容之一。从起点到终点规划一条连续且与路径上的障碍物不发生任何碰撞的路径，可使煤矿救援机器人在顶板坍塌及爆炸后散落物遍布的非结构化环境中快速到达事故现场并实施救援。

传统的全局路径规划算法有Dijkstra算法^[2]、快速扩展随机树算法^[3]、A^*算法^[4]等，局部路径规划算法有动态窗口法^[5]、人工势场法^[6]等。其中具有启发式思想的A^*算法被认为是进行静态全局路径规划最有效的方法，但其规划出的路径存在拐角过大、扩展节点较多等缺点^[7]。文献[8]将传统A^*算法的8邻域搜索扩展为24邻域搜索，改进后的A^*算法增加了搜索方向，规划的路径长度有所减小，但以牺牲时间为代价，扩展后的24邻域搜索方向不具有目的性。文献[9]通过基于象限判别的改进A^*算法寻找从起始点到目标点的最佳路径。文献[10]将传统的A^*算法改进为7×7的A^*算法，在扩展搜索邻域的基础上去除与搜索邻域同方向的子节点，并将改进A^*算法与动态窗口法相结合，实现了机器人实时避障。文献[11]优化了A^*算法的启发搜索函数，在保留关键点的基础上剔除所规划路径上的冗余节点和多余转折点。文献[12]采用Douglas-Peucker(D−P)算法提取传统A^*算法所规划路径的关键节点，通过三次样条插值函数对规划的路径进行平滑，改善了传统A^*算法所规划的路径节点多、拐弯次数多的问题，但因为传统8邻域搜索单次搜索的邻域范围小，所以需要搜索的次数多，计算量也会相应增大，不适用于规模较大的地图。

针对上述问题，本文提出一种基于改进A^*算法搜索邻域的煤矿救援机器人路径规划方法，在传统A^*算法的基础上，从原来的8邻域搜索扩展为有目的性的13邻域搜索，并采用D−P算法提取路径中的关键节点，再用三次样条插值函数对基于关键节点的整段路径进行拟合处理，得到一条相对平滑的路径。

1.   煤矿救援机器人路径规划方法

1.1   改进A^*算法

A^*算法在Dijkstra算法的基础上引入评估函数，是一种启发式搜索算法^[13-14]，评估函数的引入提高了搜索效率。A^*算法的表达式为

式中：$ F(n) $为节点$ n $的代价评估函数；$ G(n) $为煤矿救援机器人从起始点行驶到当前点$ n $所花费的实际代价；$ H(n) $为煤矿救援机器人从当前点$ n $行驶到目标点将要花费的预估代价。

$ H(n) $可采用欧几里得距离、曼哈顿距离、对角线距离表示，本文采用欧几里得距离表示，其公式为

式中：（$ {x_g} $，$ {y_g} $）为目标点g的坐标；（$ {x_n} $，$ {y_n} $）为当前点$ n $的坐标。

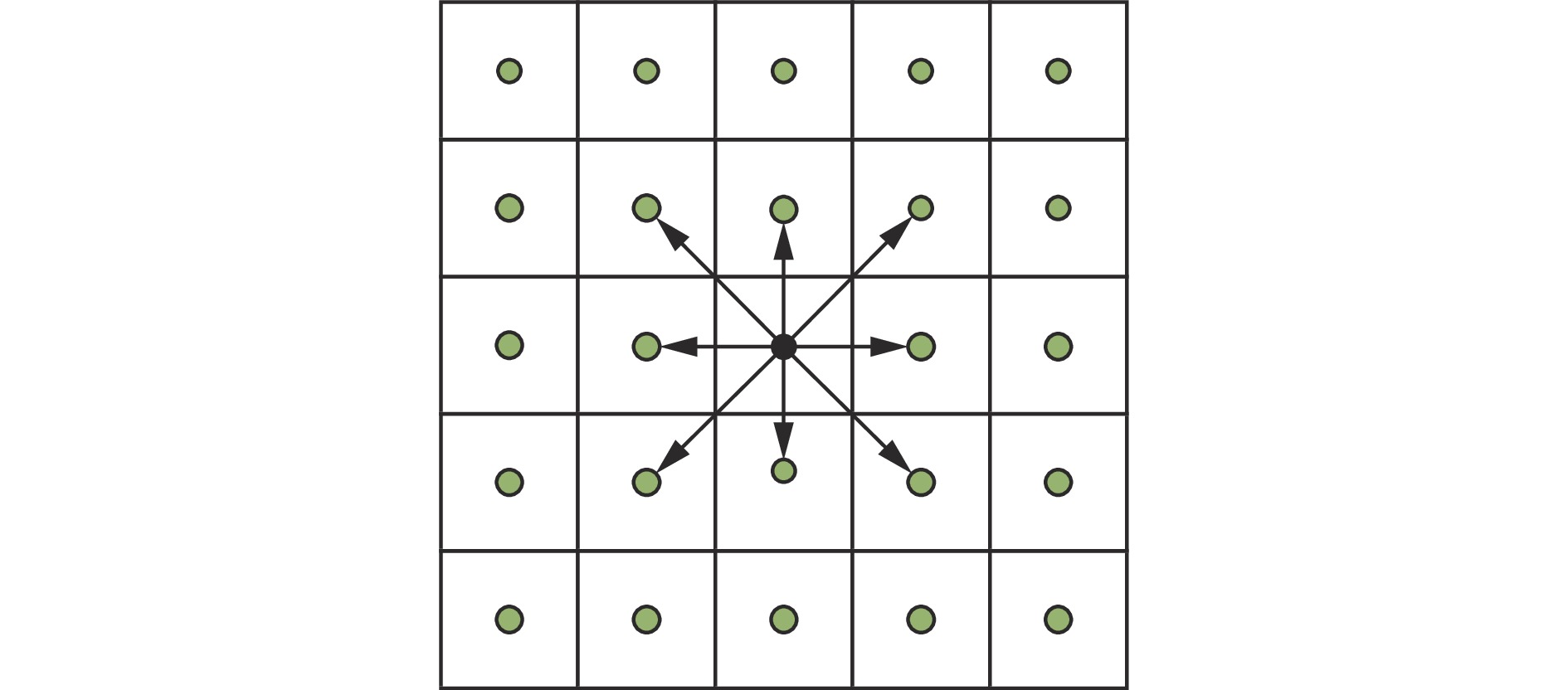
传统的A^*算法一般采用8邻域搜索方式搜索下一个要扩展的节点，其邻域搜索的角度被限定为45^o的整数倍，传统A^*算法搜索方式如图1所示。

图  1  8邻域A^*算法

Figure  1.  8 neighborhood A^* algorithm

下载: 全尺寸图片 幻灯片

为解决传统A^*算法8邻域搜索存在的问题，本文将传统A^*算法的8邻域搜索扩展为有目的性的13邻域搜索，在进行路径搜索时，先对当前点和目标点的位置关系进行判断。首先定义一个向量$ {\boldsymbol{P}} $：

当$ P_1 $≥0且$ P_2 $≤0时，目标点位于当前点的第一象限；当$ P_1 $≤0且$ P_2 $≤0时，目标点位于当前点的第二象限；$ P_1 $≤0且$ P_2 $≥0时，目标点位于当前点的第三象限；$ P_1 $≥0且$ P_2 $≥0时，目标点位于当前点的第四象限。以目标点位于当前点的第四象限为例，位置关系如图2所示，xoy为节点所在坐标系。

图  2  当前点与目标点的位置关系

Figure  2.  The positional relationship between the current point and the target point

下载: 全尺寸图片 幻灯片

当目标点位于当前点的不同象限时，改进A^*算法的搜索邻域如图3所示。改进A^*算法可以有目的性地向目标点进行扩展搜索，相比于传统的8邻域A^*算法，虽然搜索时间略有增加，但是路径节点减少，路径长度减小，平滑度有所提升，更适用于煤矿救援机器人在复杂非结构化环境中的救援工作。

图  3  改进A^*算法的搜索邻域

Figure  3.  Search neighborhood of improved A^* algorithm

下载: 全尺寸图片 幻灯片

1.2   路径平滑算法

D−P算法是一种经典的直线简化算法。该算法通过设置合适的距离阈值ɛ，有效地识别曲线特征点^[15-16]。为了优化路径，本文采用D−P算法提取改进A^*算法搜索路径中的关键节点，再采用三次样条插值函数对D−P算法提取的关键节点进行拟合，从而完成对路径的平滑处理。

D−P算法提取关键节点的步骤如下^[17]：

1) 将路径上的起点A和终点B连接，形成一条线段AB。

2) 找出路径上与线段AB距离最远的点并记为Ｃ，计算点Ｃ到线段AB的距离，记为L。

3) 将预先设置的距离阈值ε与距离L进行比较，如果ε大于L，则将线段AB作为该段路径的近似。

4) 如果ε小于L，则连接点A和点C，连接点B和点C，点Ｃ即为要提取的关键节点，分别对线段AC和BC重复步骤1)−步骤3)的处理。

5) 处理完每段路径后，依次连接所提取的关键节点，形成一条拐弯次数较少的新路径。

样条插值常用于工业设计，三次样条插值是其中应用较广泛的一种，其在保留分段低次插值多项式优点的基础上，提高了插值函数的光滑性。三次样条插值函数的定义如下：给定区间$ [a，b] $上的m个节点X（${X_1} ， {X_2}，{\boldsymbol{ \cdots}} ， {X_m} $）和这些点上的函数值$f({X_i}) = {Y_i}(i = 1，2， \cdots ，m)$，若$ S(X) $满足以下条件，则称$ S(X) $为函数$ f(X) $关于节点$ {X_1} $，${X_2} $，…，$ {X_m} $的三次样条插值函数^[18-19]：① $ S({X_i}) = {Y_i}$；② 在每个小区间$ \left[ {{X_i}，{X_{i + 1}}} \right] $上都是三次多项式；③ $ S(X) $，$ S'(X) $，$ S''(X) $在$ [a，b] $内连续。

若$ S''(X) $在$ [a，b] $内连续，则还需满足以下条件：

1.3   路径规划方法流程

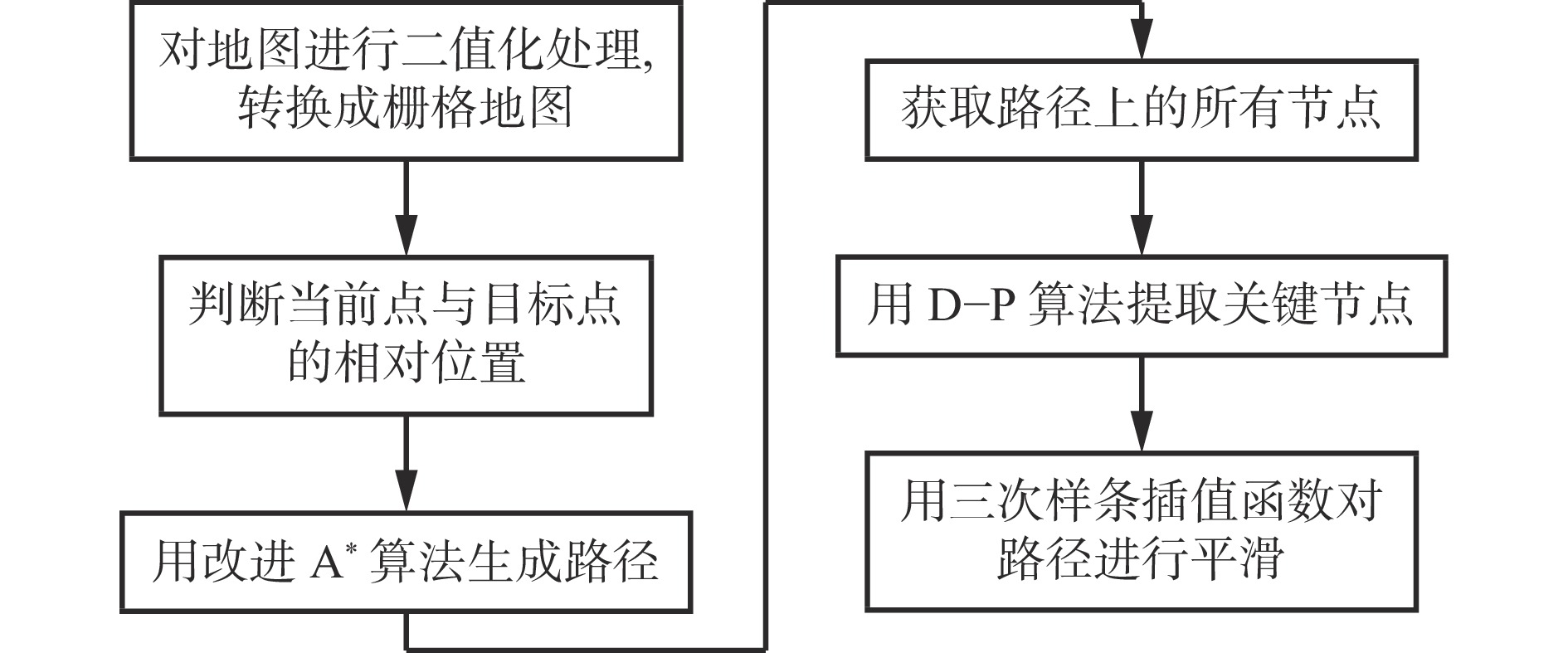
在进行路径规划前，首先，对真实环境中的地图信息进行二值化处理^[20-21]，构建栅格地图；其次，判断当前点与目标点的相对位置，利用改进A^*算法进行路径规划，得到一条从当前点到目标点的路径；再次，利用D−P算法提取路径上的关键节点；最后，利用三次样条插值函数对路径进行平滑处理。具体流程如图4所示。

图  4  煤矿救援机器人路径规划方法流程

Figure  4.  Path planning process for coal mine rescue robots

下载: 全尺寸图片 幻灯片

2.   仿真结果与分析

当矿井发生瓦斯爆炸、粉尘爆炸等灾害事故后，煤矿环境会被爆炸所产生的冲击波破坏，导致巷道内散落很多大小不一、形状各异的煤块和施工器材。为了验证改进A^*算法及路径平滑算法在该环境下的有效性，利用Matlab R2022a进行了2组仿真实验。在简单环境下将改进A^*算法与8邻域A^*算法、24邻域A^*算法、48邻域A^*算法进行对比，用不同形状的黑色图形代表灾后煤矿环境中形状各异的障碍物。由于矿井内存在一些不规则的复杂障碍物，再次在复杂环境下进行仿真实验。环境地图大小均为500 m×500 m。

简单环境下起点为(70 m，40 m)，终点为(450 m，480 m)，改进A^*算法和不同邻域A^*算法所生成的路径及平滑后的路径如图5所示，各算法性能对比见表1。由表1可知，在起点和终点相同的情况下，改进A^*算法较传统的8邻域A^*算法搜索所用的时间略长，但路径长度减小了2.45%，拐弯次数减少了41.18%，平滑后路径长度减小了1.27%，路径节点数减少了22.92%。24邻域A^*算法搜索的路径与本文算法搜索的路径长度、路径节点数相同，路径平滑前后的拐弯次数也相同，但搜索时间有所增加。与本文算法相比，48邻域A^*算法搜索所用的时间略长，但搜索的路径长度略减小，拐弯次数略减少，平滑后的路径比本文算法长。

图  5  简单环境下不同邻域A^*算法规划的路径

Figure  5.  Paths planned by different neighborhoods A^* algorithm in simple environment

下载: 全尺寸图片 幻灯片

表  1  简单环境下不同邻域A^*算法的性能对比

Table  1.  Performance comparison of different neighborhoods A^* algorithm in simple environment

算法	时间/s	路径平滑 前长度/m	路径平滑 后长度/m	路径节点数	路径平滑前拐弯次数	路径平滑后拐弯次数
8邻域A*算法	0.464	617.904	605.288	96	17	2
24邻域A*算法	0.748	602.761	597.613	74	10	2
48邻域A*算法	0.823	602.023	598.903	72	8	2
本文算法	0.619	602.761	597.613	74	10	2

下载: 导出CSV 

| 显示表格

复杂环境下起点为(30 m，40 m)，终点为(450 m，480 m)，改进A^*算法和不同邻域A^*算法所生成的路径及平滑后的路径如图6所示，各算法性能对比见表2。由表2可知，在起点和终点相同的情况下，改进A^*算法较传统的8邻域A^*算法搜索所用的时间略长，但路径长度减小了4.28%，拐弯次数减少了26.67%，平滑后路径长度减小了3.82%，路径节点数减少了28.1%。24邻域A^*算法搜索的路径与本文算法搜索的路径长度、路径节点数相同，路径平滑前后的拐弯次数也相同，但搜索时间有所增加。与本文算法相比，48邻域A^*算法搜索所用的时间略长，拐弯次数相同，但路径长度略有减小，而平滑后的路径长度、拐弯次数与本文算法一致。综合表1、表2可知，本文算法更适用于煤矿救援机器人路径规划。

图  6  复杂环境下不同邻域A^*算法规划的路径

Figure  6.  Paths planned by different neighborhoods A^* algorithm in complex environment

下载: 全尺寸图片 幻灯片

表  2  复杂环境下不同邻域A^*算法的性能对比

Table  2.  Comparison of the performance of different neighborhoods A^* algorithm in complex environment

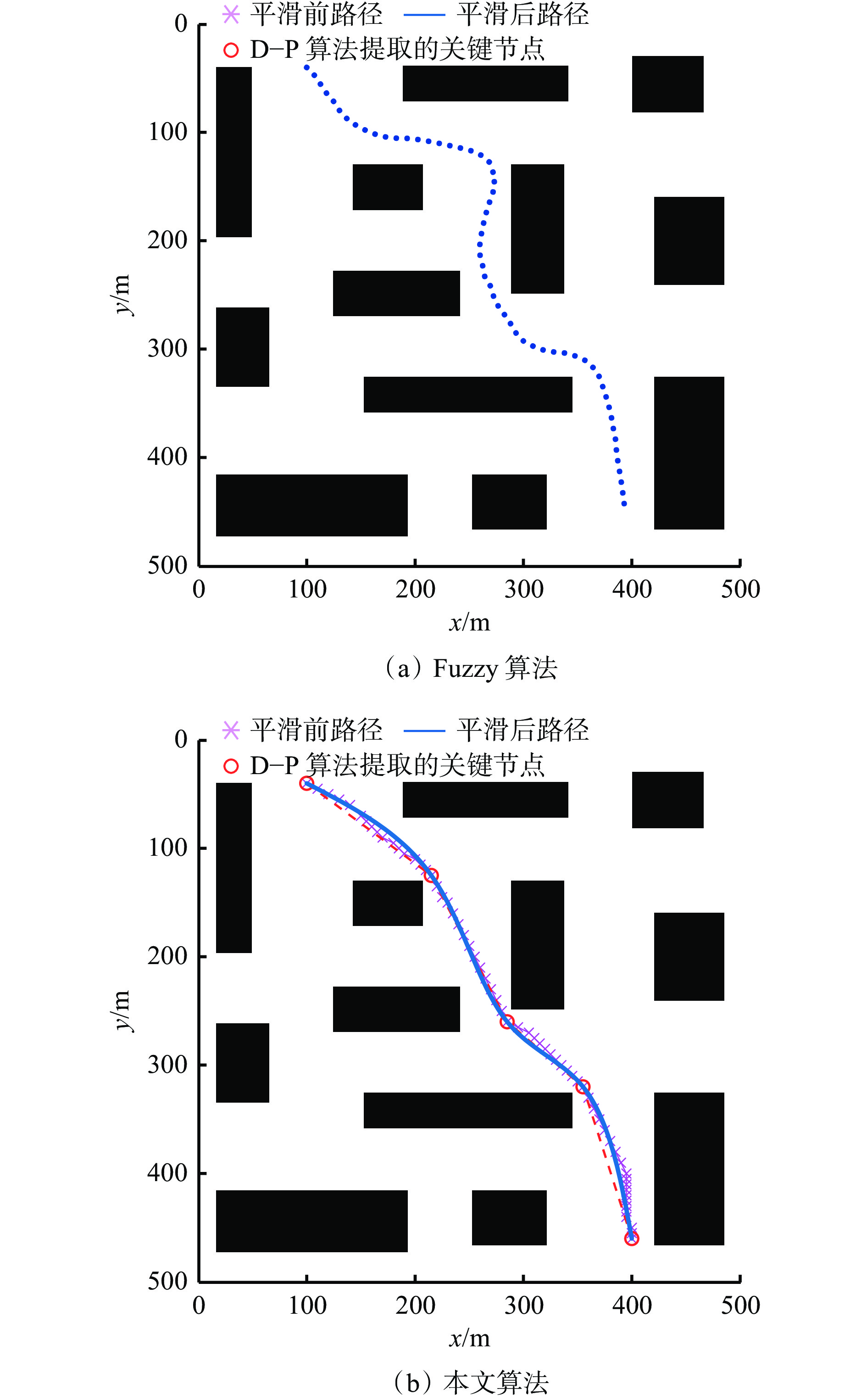
算法	时间/s	路径平滑 前长度/m	路径平滑 后长度/m	路径节点数	路径平滑前 拐弯次数	路径平滑后 拐弯次数
8邻域A*算法	0.807	707.696	699.431	121	15	8
24邻域A*算法	1.212	677.411	672.739	87	11	6
48邻域A*算法	1.361	676.673	672.739	85	11	6
本文算法	1.009	677.411	672.739	87	11	6

下载: 导出CSV 

| 显示表格

在同一环境下将本文算法和Fuzzy算法进行对比，设煤矿救援机器人的起始点为(100 m，40 m)，目标点为(400 m，460 m)，对比结果如图7所示，算法性能测试对比见表3。由图7可知，本文算法所规划的路径拐弯次数只有3，路径较为平滑。Fuzzy算法所规划的路径虽然也相对平滑，但拐弯角度过大，不利于煤矿救援机器人实施灾后救援工作。由表3可知，本文算法所规划的路径长度明显小于Fuzzy算法所规划的路径，所用时间更短，路径拐弯次数更少。减少拐弯次数可降低煤矿救援机器人工作时进行加减速以调整运动方向的频率，而路径长度的减小则可节省救援所用时间，提高救援效率。

图  7  同一环境下不同算法规划的路径对比

Figure  7.  Comparison of paths planned by different algorithms in the same environment

下载: 全尺寸图片 幻灯片

表  3  本文算法与Fuzzy算法的性能对比

Table  3.  Performance comparison between the algorithm in this article and Fuzzy algorithm

算法	路径长度/m	时间/s	拐弯次数
Fuzzy算法	695.297	1.067	5
本文算法	534.322	0.826	3

下载: 导出CSV 

| 显示表格

3.   结论

1） 改进A^*算法在传统A^*算法的基础上，将可搜索邻域个数从8个增加到13个，减少了无用搜索，能够有效解决传统A^*算法规划的路径节点数多、长度非最短的问题。

2） 采用D−P算法提取改进A^*算法搜索路径中的关键节点，再采用三次样条插值函数对D−P算法提取的关键节点进行拟合，从而完成对路径的平滑处理，解决了传统A^*算法规划的路径平滑度较差、拐弯次数较多的问题。

3） Matlab仿真结果表明：与8邻域A^*算法、24邻域A^*算法、48邻域A^*算法相比，改进A^*算法在路径长度、拐弯次数、平滑度等方面有一定优化，更适用于煤矿救援机器人路径规划；与Fuzzy算法相比，改进A^*算法路径规划所用时间更短，规划的路径长度更短，拐弯次数更少。