0.   引言

带式输送机具有结构简单、传输能力强、运输成本低、可靠性高等优点，广泛应用于煤矿井下物料、煤料的运输^[1-4]。煤矿生产过程中，若多电动机驱动的带式输送机控制方法不当，系统中个别电动机转速不同步，可能会造成输送带断裂及机电设备损坏，直接影响煤矿安全、稳定、高效运行，因此，需要对带式输送机多电动机驱动系统进行转速协同控制^[5-6]。

多电动机驱动系统转速不同步问题一般发生在带式输送机启动过程及稳定运行过程中的负载突变阶段。当输送带受到煤量连续扰动变化时，系统需要按照煤量的扰动变化情况实时给出相应的输出信号，使驱动系统中电动机的转速、转矩分配相同。多电动机驱动控制的方法主要有并行控制、主从控制、交叉耦合控制、相邻耦合控制和偏差耦合控制^[7-11]。并行控制方法通过1个控制信号同时控制多台电动机，电动机之间的相互作用会产生较高的噪声，难以保证各个电动机的控制精度一致，一般只作为步进电动机的同步控制手段^[12]。主从控制方法需对系统驱动参数进行调整，且易受负载扰动影响，系统稳定性差^[13]。交叉耦合控制方法^[14]以电动机转速差为基础，通过不同电动机对应的权重系数形成联动反馈信号，用于控制2台电动机时具有较好的应用效果。相邻耦合控制方法在对每台电动机进行控制时，需考虑被控制电动机及其相邻2台电动机的状态，当系统中电动机数目较多时，相邻耦合控制系统结构复杂^[15]。偏差耦合控制方法具备较好的综合性能，但同样存在控制系统复杂等问题。文献[16-17]分别采用转速权重系数和线性系统的矫正原理构建了新型偏差耦合控制结构，解耦了多电动机驱动系统的同步偏差与跟踪偏差，但影响了系统的可扩展能力。文献[18]利用快速非奇异终端滑模控制算法对偏差耦合控制进行了改进，提高了系统中某台电动机的同步性能，但该方法降低了系统的综合性能。文献[19-20]应用模糊控制方法对偏差耦合结构进行改进，使偏差耦合结构同步稳定性提高。文献[21]采用Super-twisting滑模控制器替换传统的转速PI控制器，使转速环具有更小的转矩脉动、更快的响应速度及更小的超调量。文献[19-21]针对系统的转速环控制器进行改进，但没有降低偏差耦合控制系统的复杂度。

针对多电动机系统传统偏差耦合控制结构复杂、系统扩展能力差且在启动及稳态运行过程中易受到负载扰动导致转速偏差的问题，提出一种带式输送机多电动机驱动系统转速同步控制方法。采用虚拟电动机，将传统偏差耦合结构中电动机之间的相互耦合关系转换为各电动机与虚拟电动机之间的耦合关系，简化了偏差耦合结构的数学模型与控制结构，提升了系统的转速同步性能和跟踪性能，简化了系统跟踪性能控制流程，增强了系统的可扩展能力。

1.   矿井带式输送机多电动机驱动系统

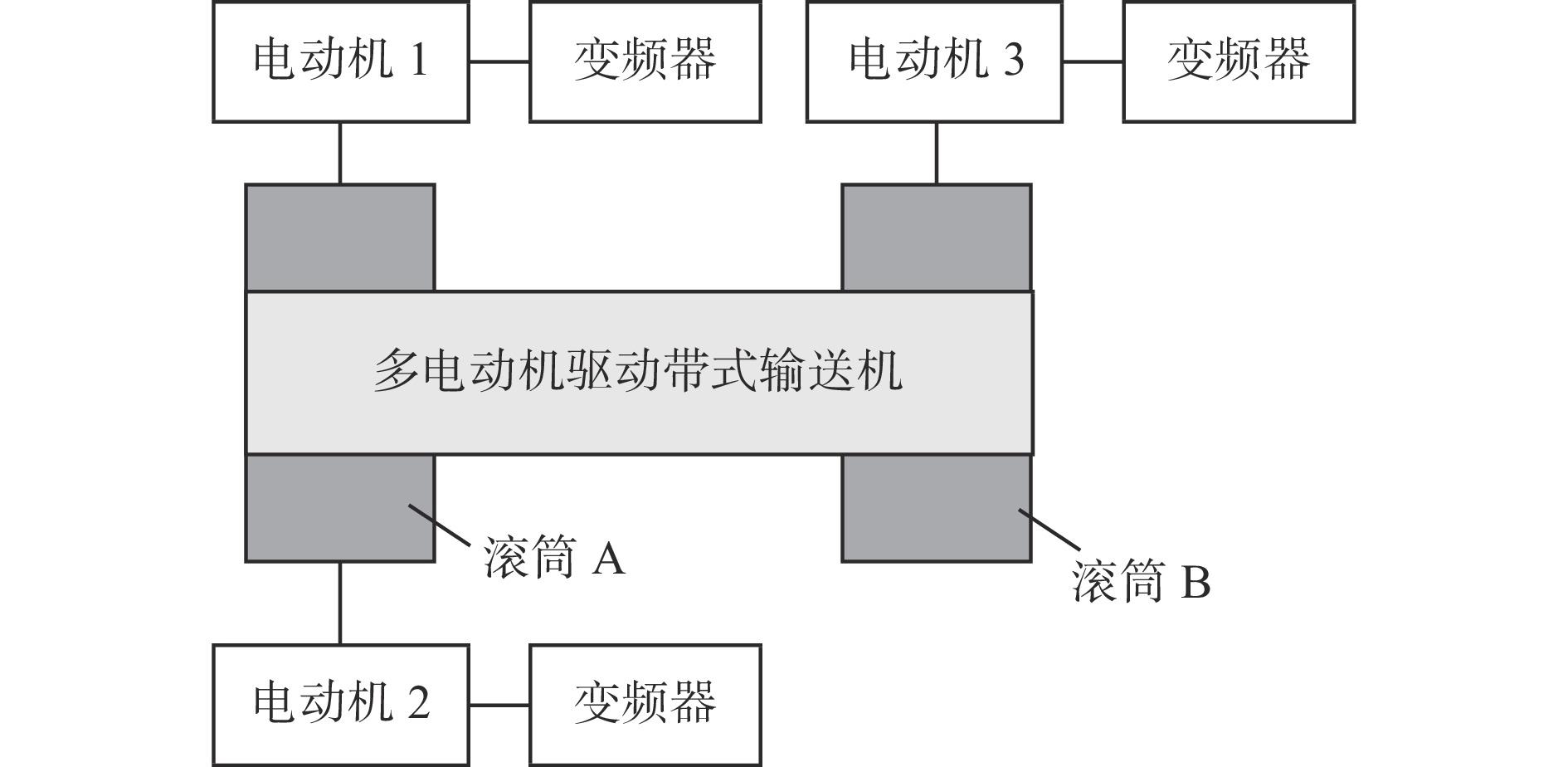
矿井带式输送机运载距离较长且具有一定的倾角，单台电动机驱动能力较弱，无法满足驱动要求，且单台电动机长时间运行会增加电动机的故障率，易导致安全事故发生。因此，矿井带式输送机常采用多电动机驱动结构，如图1所示，其中，电动机1、2与滚筒A刚性连接，电动机3单独驱动滚筒B，滚筒B与滚筒A之间柔性互联。理想状态下，通过电动机之间的控制与反馈，可实现各电动机转速同步运行。然而，由于煤炭的散料特性且实时产量的不确定性，矿井带式输送机会受到随机的负载扰动，导致各电动机间的转速不同步，对带式输送机的机械结构及输送带造成损伤，因此，需对带式输送机电动机的控制策略进行改进，以提高带式输送机启动过程与负载突变情况下的转速同步效果。

图  1  带式输送机多电动机驱动结构

Figure  1.  Multi motor drive structure of the belt conveyor

下载: 全尺寸图片 幻灯片

2.   传统偏差耦合控制分析

2.1   传统偏差耦合结构

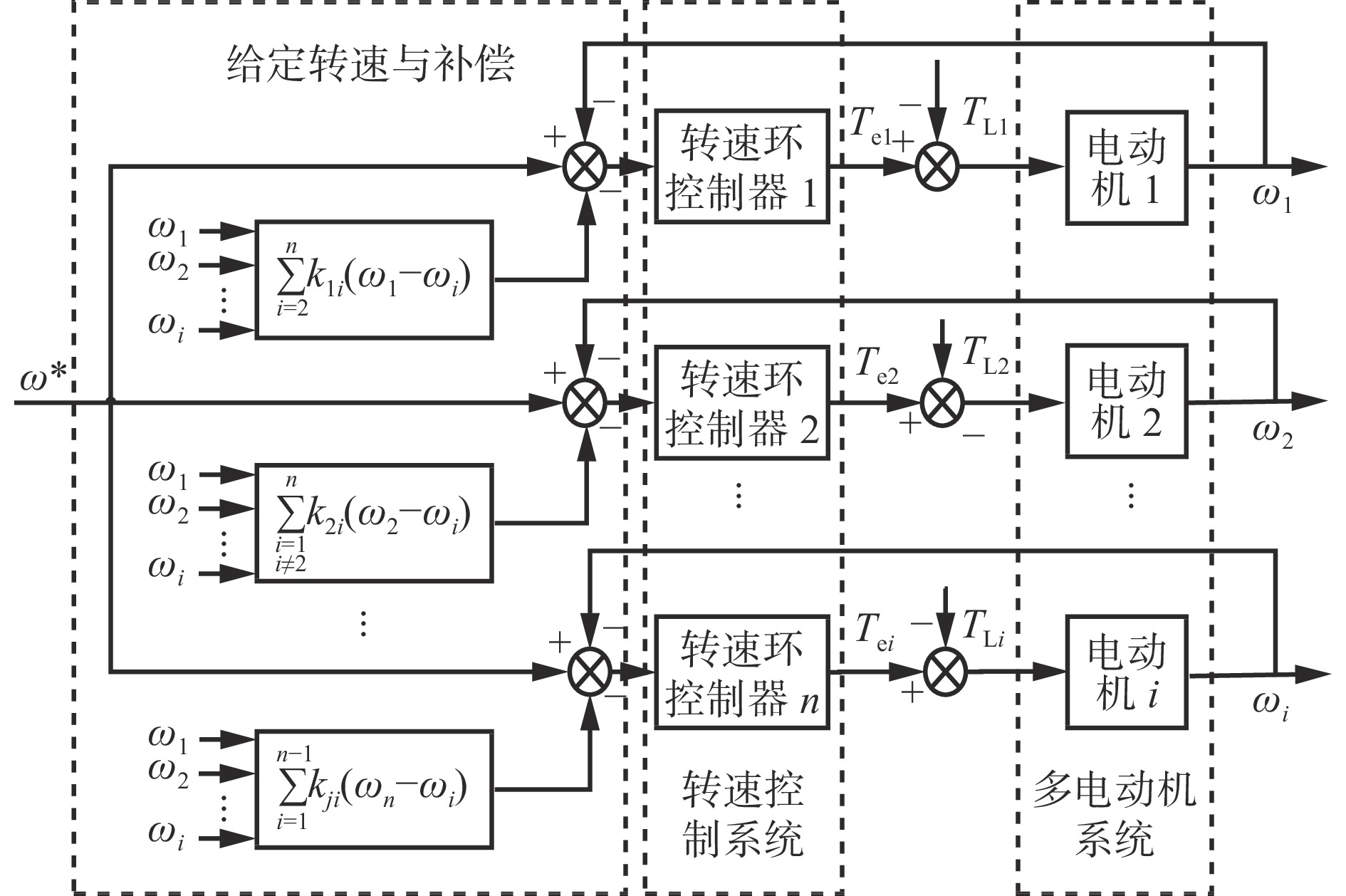
传统偏差耦合结构如图2所示，其中，$ \omega $^*为电动机的给定转速，ω_i（i=1,2,…,n，n为电动机数量）为电动机i的实际转速，k_ji（j=1,2,…,n，j≠i）为电动机j与电动机i之间的转速补偿系数，$ {T}_{{\rm{e}}i} $为电动机i的输出转矩，T_Li为电动机i的负载转矩。系统转速同步补偿器共包含$ n(n-1) $个转速差，在电动机数量较多时数学模型较复杂。当新增电动机或更换电动机时，系统中已运行的同步补偿器需要进行重新整定，工作量较大，不利于煤矿的稳定生产。

图  2  传统偏差耦合结构

Figure  2.  Traditional deviation coupling structure

下载: 全尺寸图片 幻灯片

为了减少多电动机驱动系统的同步偏差，在每台电动机转速环控制器的输入环节加入同步补偿器，改善整个多电动机系统的转速同步性能，该补偿器由自身电动机与系统其他电动机之间的转速差构成。

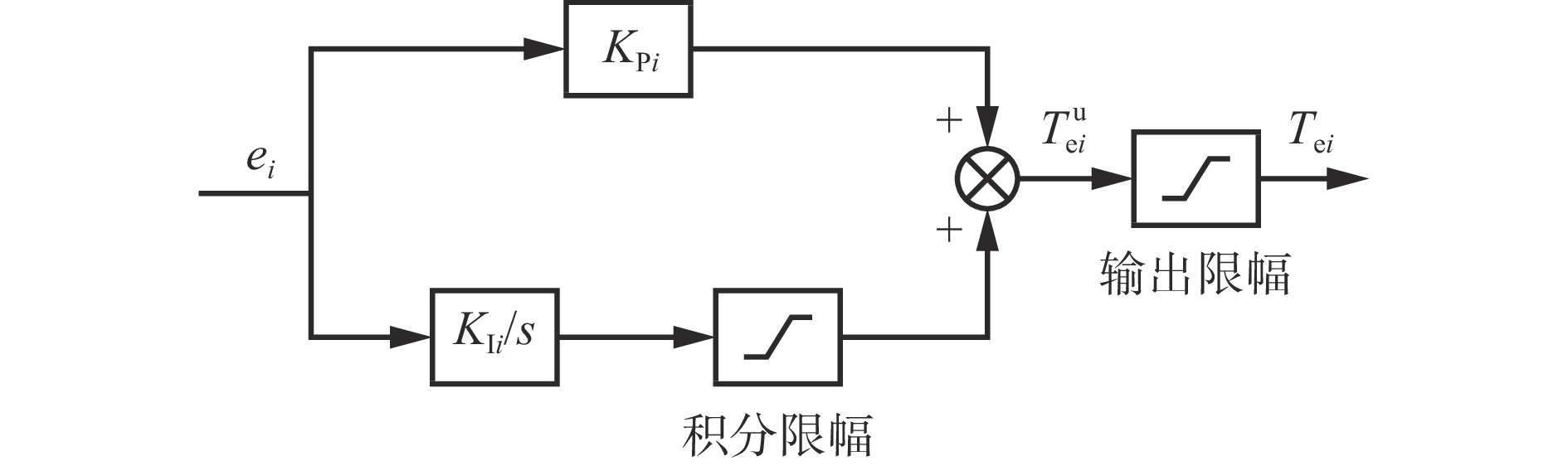
式中$ {\omega }_{\mathrm{b}j} $为电动机j的补偿转速。

为了保证系统的稳定性，在传统PI控制器结构中引入积分限幅和输出限幅2个环节，如图3所示，其中，e_i为电动机i的转速偏差，$ {K}_{{\rm{P}}i} $为电动机i转速环控制器的比例系数，$ {K}_{{\rm{I}}i} $为电动机i转速环控制器的积分系数，s为复参数，$ {T}_{{\rm{e}}i}^{{\rm{u}}} $为电动机$ i $未经输出限幅的输出转矩。

图  3  PI控制器结构

Figure  3.  PI controller structure

下载: 全尺寸图片 幻灯片

整定方法为

式中：$ \alpha $为PI控制器的转速环带宽；$ {J}_{i} $为电动机i的转动惯量；$ \zeta $为电动机的阻尼系数。

电动机$ i $的等效传递函数为

2.2   传统偏差耦合机构启动性能分析

在系统启动阶段，仅对电动机$ j $施加负载转矩$ {T}_{{\rm{L}}j} $，其他电动机空载启动，启动过程满足以下条件：

其他电动机具有相同的转动惯量$ {J}_{i} $和转速$ {\omega }_{i} $，且额定转矩和负载转矩都相等。

电动机$ i $的输出转矩为

式中：${T}_{{\rm{e}}i}^{{\rm{u}}1}$为电动机$ i $的跟踪偏差转矩，表示电动机$ i $的转速跟踪偏差对应的输出转矩；${T}_{{\rm{e}}i}^{{\rm{u}}2}$为电动机$ i $补偿转速${\omega }_{{\rm{b}}i}$对应的输出转矩，即电动机$ i $的补偿转矩。

系统启动阶段，各电动机的跟踪偏差转矩均大于$1.2{T}_{{\rm{N}}}$（T_N为电动机额定转矩）。由式（5）可知，电动机$ j $与其他电动机的转速差$\mathrm{\Delta }\omega =({\omega }_{j}-{\omega }_{i}) ＜ 0$。因此，电动机$ j $的补偿转矩为

将式（7）代入式（6）可得电机动j的输出转矩${T}_{{\rm{e}}j}^{{\rm{u}}}={T}_{{\rm{e}}j}^{{\rm{u}}1}+{T}_{{\rm{e}}j}^{{\rm{u}}2} ＞ {T}_{{\rm{e}}j}^{{\rm{u}}1} ＞ 1.2{T}_{{\rm{N}}}$。

其他电动机的补偿转矩为

式中k为传统偏差耦合结构中转速环补偿系数。

电动机i的输出转矩${T}_{{\rm{e}}i}^{{\rm{u}}}={T}_{{\rm{e}}i}^{{\rm{u}}1}+{T}_{{\rm{e}}i}^{{\rm{u}}2} ＜ {T}_{{\rm{e}}i}^{{\rm{u}}1}$。

通过以上分析可知，传统偏差耦合结构的电动机启动过程中，负载电动机j的输出转矩较补偿前没有减少反而增加了，除电动机$ j $以外的其他电动机，只有当转速差$ \Delta \omega $增加到一定值时，补偿器的补偿转速才能将输出转矩缩小到控制器的额定值以下，起到减小跟踪偏差的作用。

2.3   传统偏差耦合机构负载突变性能分析

带式输送机在稳定运行期间，系统中控制器工作在线性区，所有电动机的转速输出都可以用传递函数进行表达。以电动机$ i $为例，影响其输出转速的输入量有转速给定、负载扰动与其他电动机转速，电动机i转速的传递函数为^[17]

式中：F为转速控制环传递函数；G为系统传递函数；G_i和G_j分别为电动机i和电动机j控制系统的传递函数。

3.   改进的偏差耦合结构分析

3.1   改进的偏差耦合结构

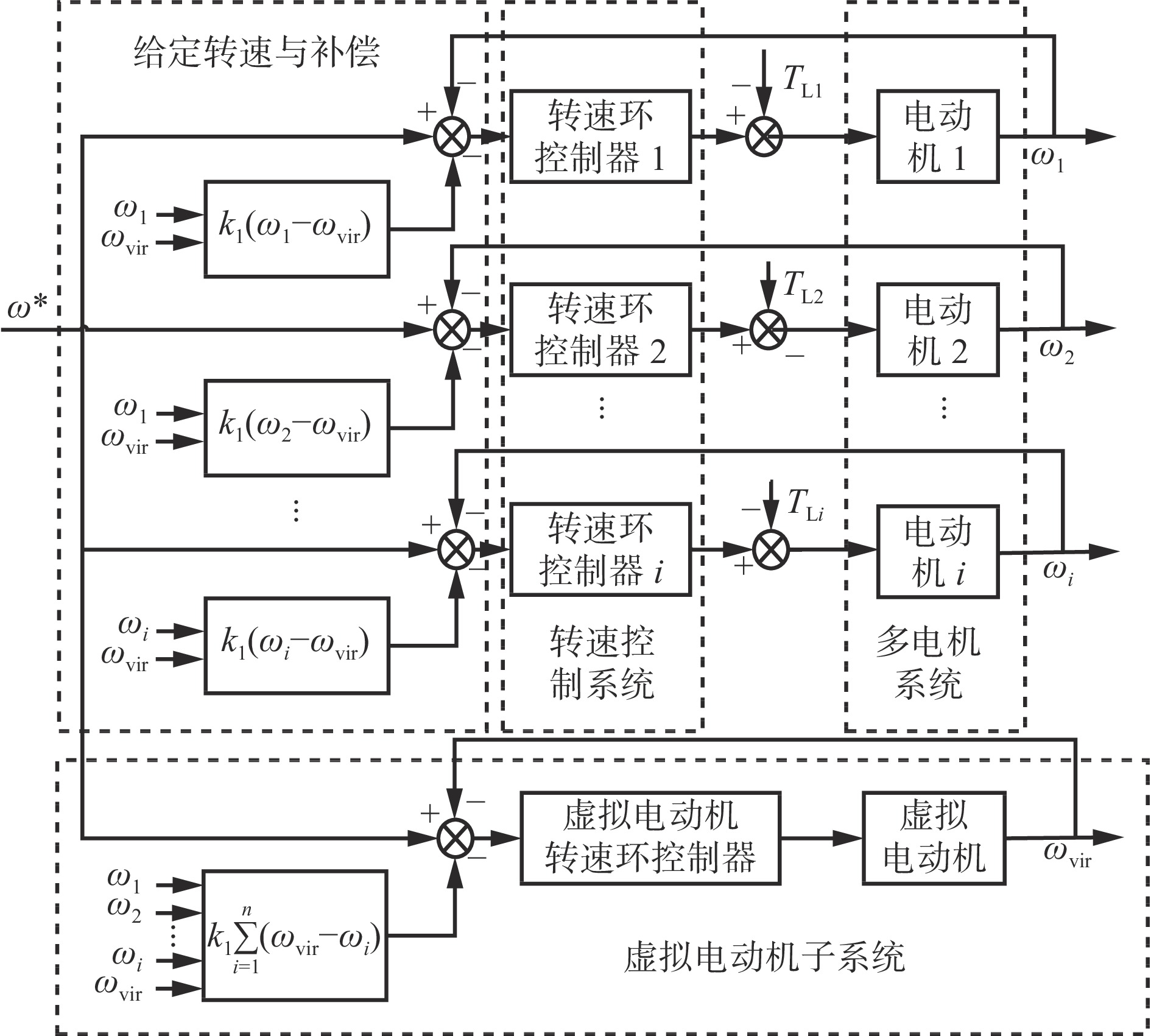
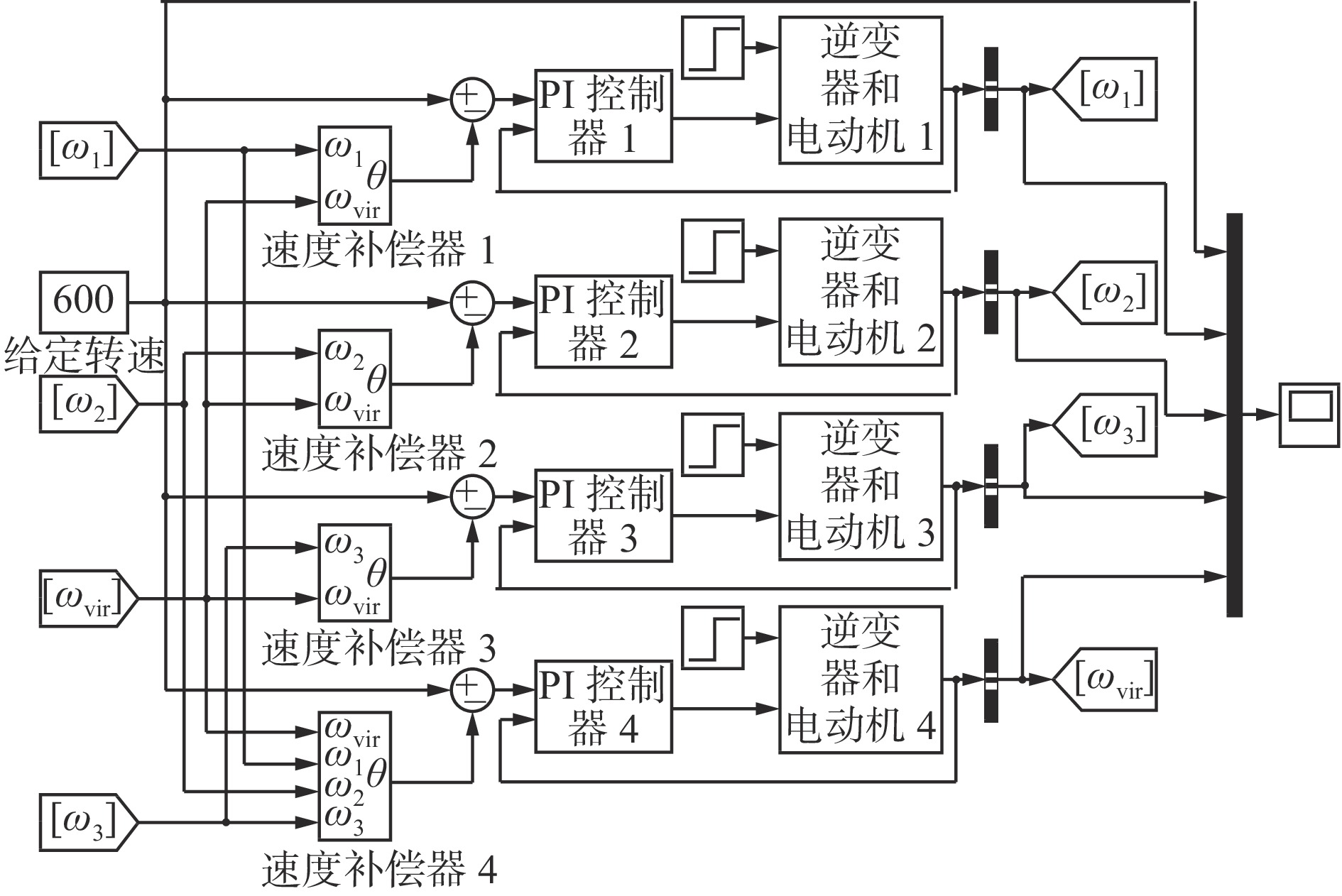
为了降低传统偏差耦合系统的复杂程度，引入虚拟电动机对传统偏差耦合结构进行改进，具体结构如图4所示，其中，$ {k}_{1} $为所有补偿器统一的补偿系数，$ {\omega }_{{\rm{vir}}} $为虚拟电动机的转速。当系统电动机为$ n $台时，系统转速同步补偿器共包含的转速差数为$ 2n $。在系统需要对电动机数量进行改变时，仅需在虚拟电动机转速同步补偿器中加入新的转速变量，原系统的转速同步补偿器则无需改变，增强了系统可扩展性能。

图  4  改进偏差耦合结构

Figure  4.  The improved deviation coupling structure

下载: 全尺寸图片 幻灯片

改进偏差耦合结构的转速补偿器数学表达式简化为自身电动机与虚拟电动机的转速差。

此时的虚拟电动机等效传递函数$ \mathrm{为} $

式中$ {J}_{{\rm{vir}}} $为虚拟电动机的转动惯量。

3.2   改进偏差耦合结构启动性能分析

在与传统偏差耦合结构相同的启动前提条件下，改进偏差耦合控制结构中虚拟电动机对应的转动惯量分别取$ {J}_{{\rm{vir}}1}，{J}_{{\rm{vir}}2}，{J}_{{\rm{vir}}3} $，并令${J}_{{\rm{vir}}1} ＜ {J}_{{\rm{vir}}2} ＜ {J}_{{\rm{vir}}3}$。

电动机$ j $的补偿转速$ {\omega }_{{\rm{b}}j} $对应的转矩输出值为

为了减小跟踪偏差，需要使输出转矩满足${T}_{{\rm{e}}j}^{{\rm{u}}}= {T}_{{\rm{e}}j}^{{\rm{u}}1}+{T}_{{\rm{e}}j}^{{\rm{u}}2} ＜ {T}_{{\rm{e}}j}^{{\rm{u}}1}$，即${\omega }_{{\rm{vir}}} ＜ {\omega }_{j}$。同理，电动机$ i $转矩输出值为

同样，需满足${\omega }_{{\rm{vir}}} ＜ {\omega }_{i}$要求，进而减小跟踪偏差。

当${\omega }_{{\rm{vir}}}＜{\omega }_{j}＜{\omega }_{i}$时，在改进偏差耦合控制结构的系统启动时期，补偿器输出的补偿转速可将输出转矩$ {T}_{{\rm{e}}i}^{{\rm{u}}} $减小到一定值，使得跟踪偏差也一起减小。又因$ {J}_{{\rm{vir}}} $与$ {\omega }_{{\rm{vir}}} $成反比关系，所以当$ {J}_{{\rm{vir}}} $增大时，$ {\omega }_{{\rm{vir}}} $，$ {T}_{{\rm{e}}i}^{{\rm{u}}2} $，$ {T}_{{\rm{e}}j}^{{\rm{u}}2} $同时减小，从而达到减小各电动机跟踪偏差的目的。

在系统启动过程中，电动机之间转动惯量的偏差也将导致同步偏差。电动机$ j $与电动机$ i $之间的同步偏差转矩为

式中$ {T}_{{\rm{e}}i}^{{\rm{u}}}\left({J}_{{\rm{vir}}1}\right) $为在转动惯量为$ {J}_{{\rm{vir}}1} $时对应的转矩。

当$ {J}_{j}＞ {J}_{i} $时，因为$ {J}_{{\rm{vir}}} $与$ {\omega }_{{\rm{vir}}} $成反比关系，增加$ {J}_{{\rm{vir}}} $会使电动机$ j $与电动机$ i $之间的同步偏差转矩减小，电动机$ j $与电动机$ i $之间的同步偏差将减小，进而提升系统在启动过程中的同步性。

3.3   改进偏差耦合结构负载突变性能分析

带式输送机在稳定运行期间，系统中控制器工作在线性区，所有电动机的转速输出都可以用传递函数进行表达。改进偏差耦合结构中电动机$ i $转速的传递函数为

对比式(15)和式(9)可知，式(9)中本身负载扰动及其他电动机跟踪偏差均大于式(15)中的对应部分，因此，在负载扰动时，改进偏差耦合结构产生的总跟踪偏差小于传统偏差耦合结构，性能有所提高。

3.4   虚拟电动机转动惯量

对于改进偏差耦合结构，增大虚拟电动机转动惯量${J}_{{\rm{vir}}}$可以提高系统的同步性能，但也增加了电动机的启动时间，需要合理选择。

在多电动机驱动系统的启动阶段，系统中各电动机需具备一定的启动加速度，加速度最小值为

式中${T}_{{\rm{N}}i} $为电动机i的额定转矩。

虚拟电动机的加速度为

式中${T}_{{\rm{Nvir}}}$为虚拟电动机的额定转矩。

当要求系统各电动机启动时间为最大加速度启动时间的λ倍时，可得

式中$ \mathrm{\lambda } $为可调参数。

当${T}_{{\rm{N}}i}={T}_{{\rm{L}}i}$时，电动机加速度最小；当虚拟电动机额定转矩${T}_{{\rm{Nvir}}}\mathrm{与}\mathrm{最}\mathrm{大}\mathrm{额}\mathrm{定}\mathrm{转}\mathrm{矩}{T}_{{\rm{NM}}}$相等时，有

当所有电动机的额定转矩、转动惯量相同时，虚拟电动机的转动惯量取值范围为$\left[6{J}_{i},6\mathrm{\lambda }{J}_{i}\right] $。

4.   仿真分析对比

在Matlab/Simulink平台，分别对采用传统和改进的偏差耦合结构的三驱永磁同步电动机（Permanent-Magnet Synchronous Motor，PMSM）系统的启动过程、突加负载进行仿真分析，主要仿真参数见表1，其中，R_s为定子电阻，L_d和L_q分别为电动机d轴和q轴同步电感，Ψ_f为转子磁链，P_n为电动机的磁极对数。

表  1  PMSM主要仿真设计参数

Table  1.  Main simulation design parameters of PMSM

参数	取值
Rs/Ω	2.875
Ld/mH	0.85
Lq/mH	0.85
Ψf/Wb	0.175
J/(kg·m2)	0.825×10−3
Jvir/(kg·m2)	7.425×10−3
Pn	2
TN/(r·min−1)	600

下载: 导出CSV 

| 显示表格

4.1   传统偏差耦合结构仿真分析

传统偏差耦结构仿真模型如图5所示。设置仿真时间t=5 s，给定转速$ {\omega }^{*}=600\;\mathrm{r}/\mathrm{m}\mathrm{i}\mathrm{n} $，在$ t=2.5\;\mathrm{s} $时，对系统突然施加$ {T}_{{\rm{L}}}=10\;\mathrm{N}\cdot \mathrm{m} $的负载。

图  5  传统结构仿真模型

Figure  5.  Traditional structure simulation model

下载: 全尺寸图片 幻灯片

采用传统偏差耦合结构的3台电动机的速度跟踪曲线如图6所示。

图  6  传统结构速度跟踪曲线

Figure  6.  Speed tracking curve of the traditional structure

下载: 全尺寸图片 幻灯片

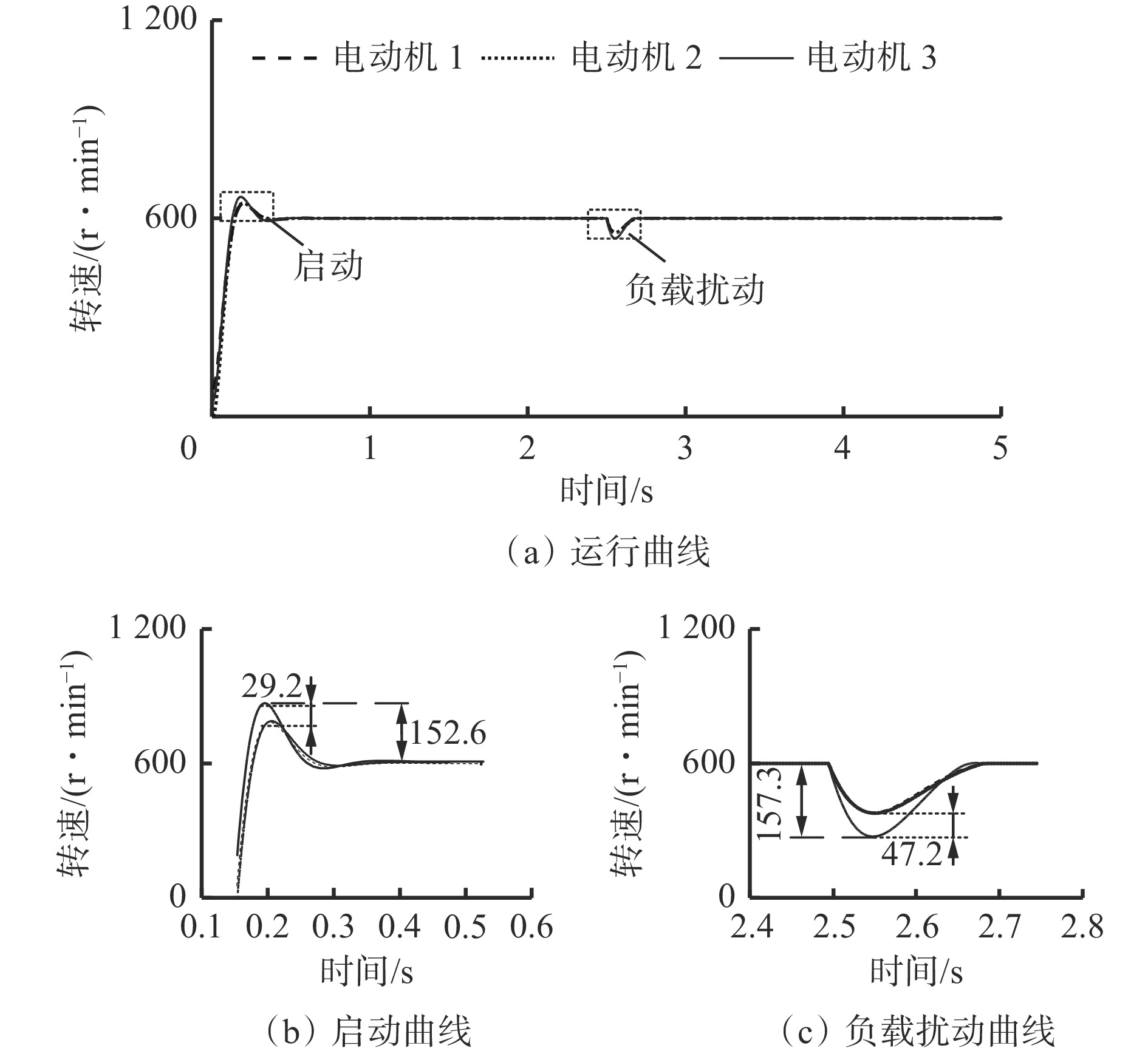
由图6可看出，传统的偏差耦合结构在启动过程及突加负载情况下，电动机1和电动机2的跟踪曲线吻合度较高，但是与电动机3的跟踪效果存在较大差异，其中电动机3突加负载时的转速偏差最明显。具体偏差见表2，其中τ₁，τ₂，τ₃分别为电动机1，2，3对应的最大转速偏差，τ₁₂，τ₁₃，τ₂₃分别为电动机1和电动机2、电动机1和电动机3、电动机2和电动机3之间的最大跟踪偏差。

表  2  传统偏差耦合结构启动过程跟踪偏差

Table  2.  Process tracing error of traditional deviation coupling structure initiation

偏差类型	τ1	τ2	τ3	τ12	τ13	τ23
转速/（r·min−1）	117.9	118.3	152.6	5.2	28.6	29.2

下载: 导出CSV 

| 显示表格

由表2可知，单电动机与给定转速偏差的最大值为152.6 r/min，τ₁，τ₂，τ₃的平均值为129.6 r/min，各电动机间的同步偏差最大达29.2 r/min，非刚性连接的电动机转速同步效果较差。

突加负载时的跟踪偏差见表3。可看出在突加负载情况下，多驱动系统电动机作出调整时，负载电动机与非负载电动机的同步性较差，跟踪偏差最大值达45.4 r/min。相比之下，因为刚性连接结构的存在，电动机1和电动机2之间的同步偏差相对较小，最大同步偏差为6.9 r/min。

表  3  传统偏差耦合结构负载突变过程跟踪偏差

Table  3.  Traditional deviation coupling structure load mutation process trace error

偏差类型	τ1	τ2	τ3	τ12	τ13	τ23
转速（r·min−1）	109.6	110.2	157.3	6.9	45.4	47.2

下载: 导出CSV 

| 显示表格

4.2   改进偏差耦合结构的仿真分析

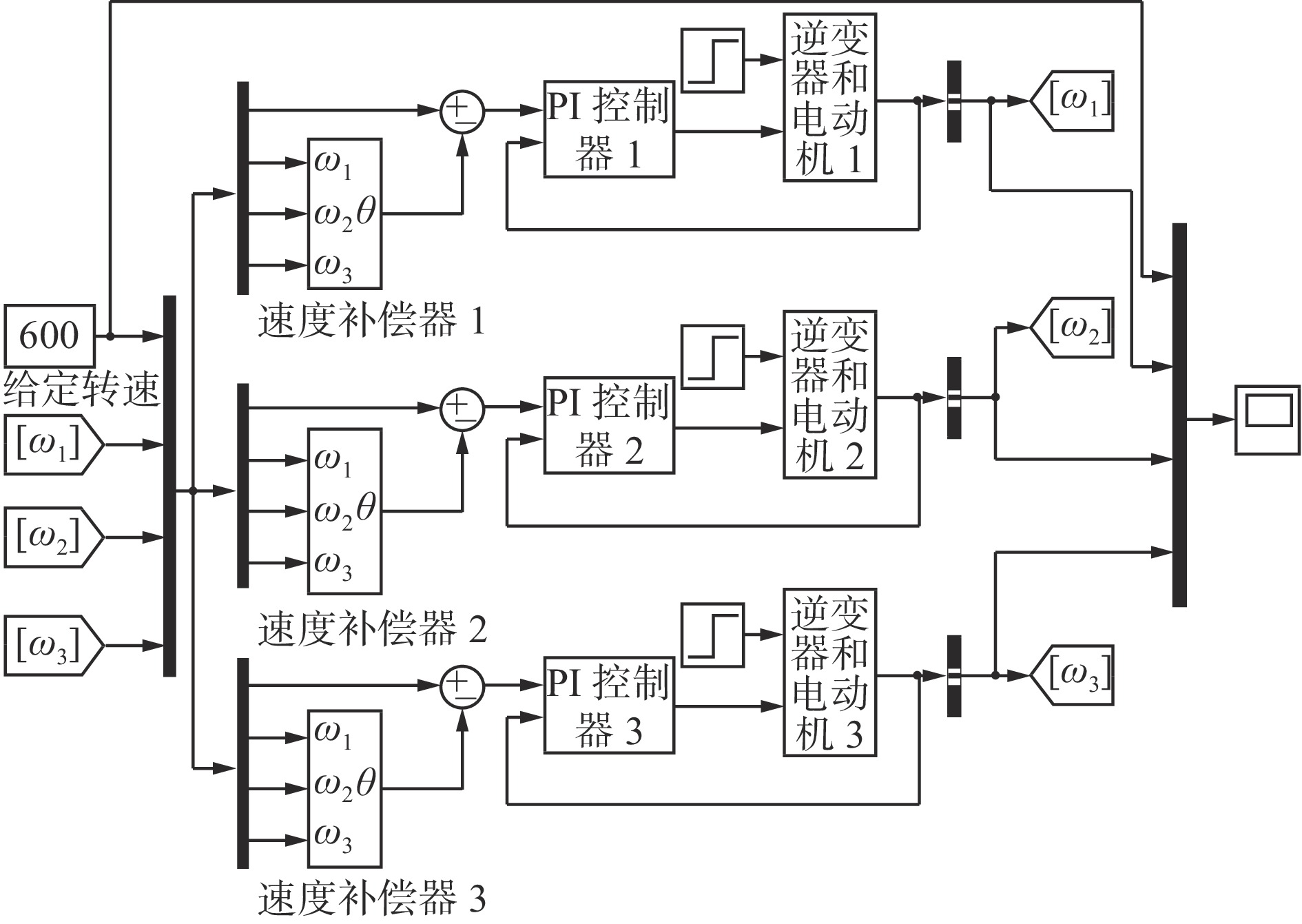
改进偏差耦合结构仿真模型如图7所示，基本仿真参数与传统偏差耦合结构参数相同。

图  7  改进结构仿真模型

Figure  7.  Improved structure simulation model

下载: 全尺寸图片 幻灯片

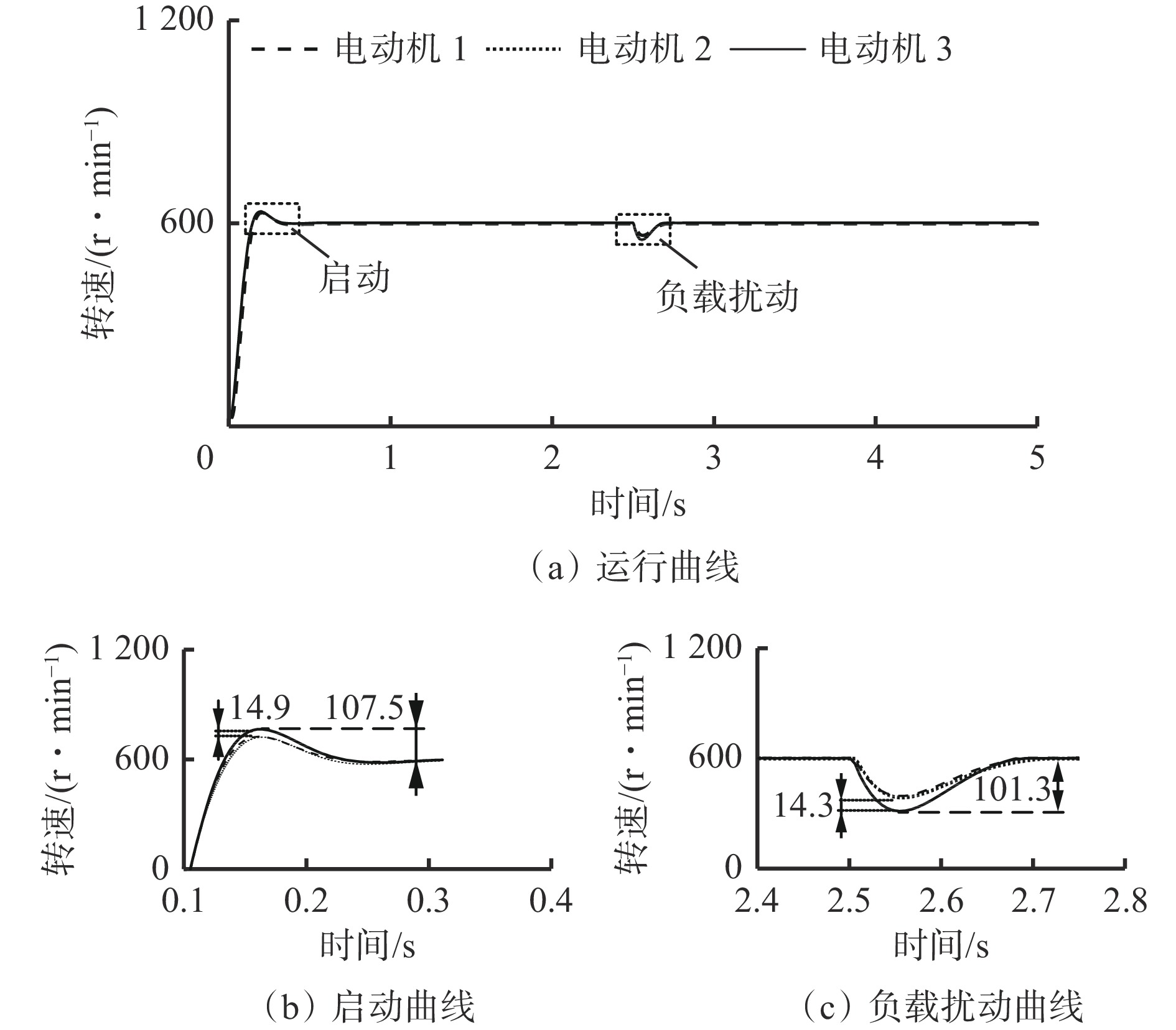
改进偏差耦合结构的转速跟踪曲线如图8所示。可看出在系统启动初期，各电动机之间的整体同步性能得到了很好的改善，刚性连接的电动机1与电动机2的同步性能较好，可以有效避免启动过程中高负载情况下对电动机组机械结构的损伤。对于突加负载情况，电动机1与电动机2同样具备较好的跟踪效果，能够在负载突变情况下，保证系统中电动机的转速同步。改进偏差耦合结构启动过程跟踪偏差见表4。

图  8  改进偏差耦合结构的跟踪偏差

Figure  8.  Tracking error of the improved deviation coupling structure

下载: 全尺寸图片 幻灯片

表  4  改进偏差耦合结构启动过程跟踪偏差

Table  4.  Process trace error of improved deviation coupling structure initiation

偏差类型	τ1	τ2	τ3	τ12	τ13	τ23
转速/（r·min−1）	90.4	89.2	107.5	1.2	14.1	14.9

下载: 导出CSV 

| 显示表格

由表4可知，改进偏差耦合结构中，将简化后的转速同步补偿器输出结果和跟踪偏差作为电动机的转速环控制器输入。在系统的启动阶段，给定转速保障了电动机的启动速度并降低了跟踪偏差，使τ₁，τ₂，τ₃的平均值降低至95.7 r/min，与传统结构相比下降了33.9 r/min。同时，刚性连接的2台电动机之间的同步偏差τ₁₂降低了4.0 r/min。

对改进偏差耦合结构系统进行突加负载仿真，得到跟踪偏差结果，见表5。可看出改进的偏差耦合结构根据各电动机实时转速的不同，使其对应的同步补偿器输出各不相同，从而可以改善系统的同步性能，使单电动机的最大速度偏差和系统中双电动机之间的跟踪偏差均明显降低。与表3中数据对比可知，单电动机的最大速度偏差降低了56.0 r/min，电动机1和电动机2之间的同步偏差与传统结构保持同一水平，τ₁₃和τ₂₃分别减少了30.5，32.9 r/min。刚性与柔性连接电动机之间的同步偏差τ₁₃，τ₂₃平均值为14.6 r/min，比传统结构降低了31.7 r/min。

表  5  改进偏差耦合结构负载突变过程跟踪偏差

Table  5.  Improved deviation coupling structure load mutation process trace error

偏差类型	τ1	τ2	τ3	τ12	τ13	τ23
转速/（r·min−1）	85.8	84.7	101.3	1.7	14.9	14.3

下载: 导出CSV 

| 显示表格

由表2—表5的偏差结果可知，改进偏差耦合结构系统电动机启动时，柔性连接的电动机同步偏差的最大值及平均值均小于传统的偏差耦合结构，保证了启动过程中滚筒的同步性能。当多电动机系统发生负载突变时，改进偏差耦合结构各电动机的跟踪偏差较小，同步偏差也有所降低。因此，在运行条件一定时，相比于传统的偏差耦合结构，改进的偏差耦合结构在多电动机系统启动及负载突变的情况下，表现出了较好的跟踪和同步性能。

5.   结论

1） 通过引入虚拟电动机，对多电动机驱动系统的偏差耦合结构进行优化改进，减少了系统参数，降低了系统整体的转速跟踪偏差，增强了系统的可扩展性；推导出了虚拟电动机转动惯量的取值范围，保证了系统的启动转矩要求。

2） 系统启动阶段，改进偏差耦合结构中刚性连接与柔性连接电动机之间具备较好的同步性能。与传统偏差耦合结构相比，采用改进结构后，刚性连接电动机之间的同步偏差减少了4.0 r/min，使启动过程中主驱动滚筒具备良好的初始动力。

3） 采用改进结构后，在负载突变时，刚性连接电动机的同步偏差为1.7 r/min，刚性与柔性连接电动机之间的同步偏差平均值为14.6 r/min，比传统耦合偏差结构分别降低了5.2，31.7 r/min，可有效降低负载突变对电动机机械结构的损伤。