0.   引言

供液系统作为综采工作面的关键，为液压支架和采煤机喷雾降尘提供液压动力。《中国制造2025−能源装备实施方案》中明确提出：要朝着向“智能化清洁高效集成供液系统”方向快速发展^[1]，重点提升我国综采工作面自动化开采和供液技术水平。近年来，7 m以上的大采高、超大采高^[2-3]液压支架的快速移架、安全防护、高工作阻力和高初撑力对供液系统的供液流量有了更高的需求，乳化液泵作为供液系统动力源，其供液能力不足是制约大流量供液技术发展的重要瓶颈。综采工作面供液系统存在供液压力波动大、压力控制不精准等问题，无法达到精准供液的要求，因此供液系统稳压控制技术是供液系统智能化控制技术的主要研究热点^[4]。

在倡导“矿井绿色生态、安全高产高效”理念^[5-7]的背景下，许多学者对供液系统供液能力不足和稳压供液的问题进行了研究。张占东等^[8]、杨国来等^[9]提出了一种乳化液泵站多泵并联的流量调节方法，该方法根据液压支架压力变化，按需启动乳化液泵进行供液，以达到稳压供液目标。石建华等^[10]将变频器加入到乳化液泵站，通过变频器控制电动机转速，从而实现乳化液泵的流量与压力调节。陈伟等^[11]提出将电磁卸荷阀与变频控制相结合的压力调节方式，把6台低流量乳化液泵改为2 台大流量乳化液泵。上述基于多泵协同的控制方法虽在流量调节速度方面响应快，但存在流量控制精度低且不能实现无级调节的问题，加入变频器对乳化液泵进行改进后，在应对压力突变特征时，变频调速执行时间会导致控制动作严重滞后。李文华等^[12]、王建国等^[13]提出了基于模糊PID（Proportion Integral Differential）的供液控制方法，通过模糊PID控制器输出信号给伺服电动机驱动器，从而调节电动机转速，改变泵流量。胡相捧等^[14]提出了基于神经网络的供液控制方法，采用梯度下降法和有监督的Hebb学习规则对输出层和隐含层的权值系数进行调整，从而得到PID控制参数。基于智能算法的控制方法相较于多泵协同控制策略可更精确地调节供液流量，但当乳化液泵为单台大流量泵时，乳化液泵负载变大，增加了变频调节时间。

模糊神经网络（Fuzzy Neural Network，FNN）算法将模糊逻辑与神经网络相结合，动态响应快，控制精度高，具有较强的鲁棒性和适应能力^[15]，但易陷入局部极小值。免疫算法（Immune Algorithm，IA）克服了一般寻优过程中不可避免的“早熟”问题，可求得全局最优解。粒子群（Particle Swarm Optimization，PSO）算法是一种基于迭代的优化算法，通过迭代搜寻最优值。因此，本文将IA和PSO算法相结合，得到免疫粒子群（Immune PSO，IPSO）算法，并提出一种免疫粒子群优化模糊神经网络PID（IPSO−FNN−PID）算法，设计了IPSO−FNN−PID控制器，将该控制器应用于供液系统稳压控制，可有效减少变频调节时间，大幅提高流量控制精度，达到供液系统稳压控制目的。

1.   供液系统结构

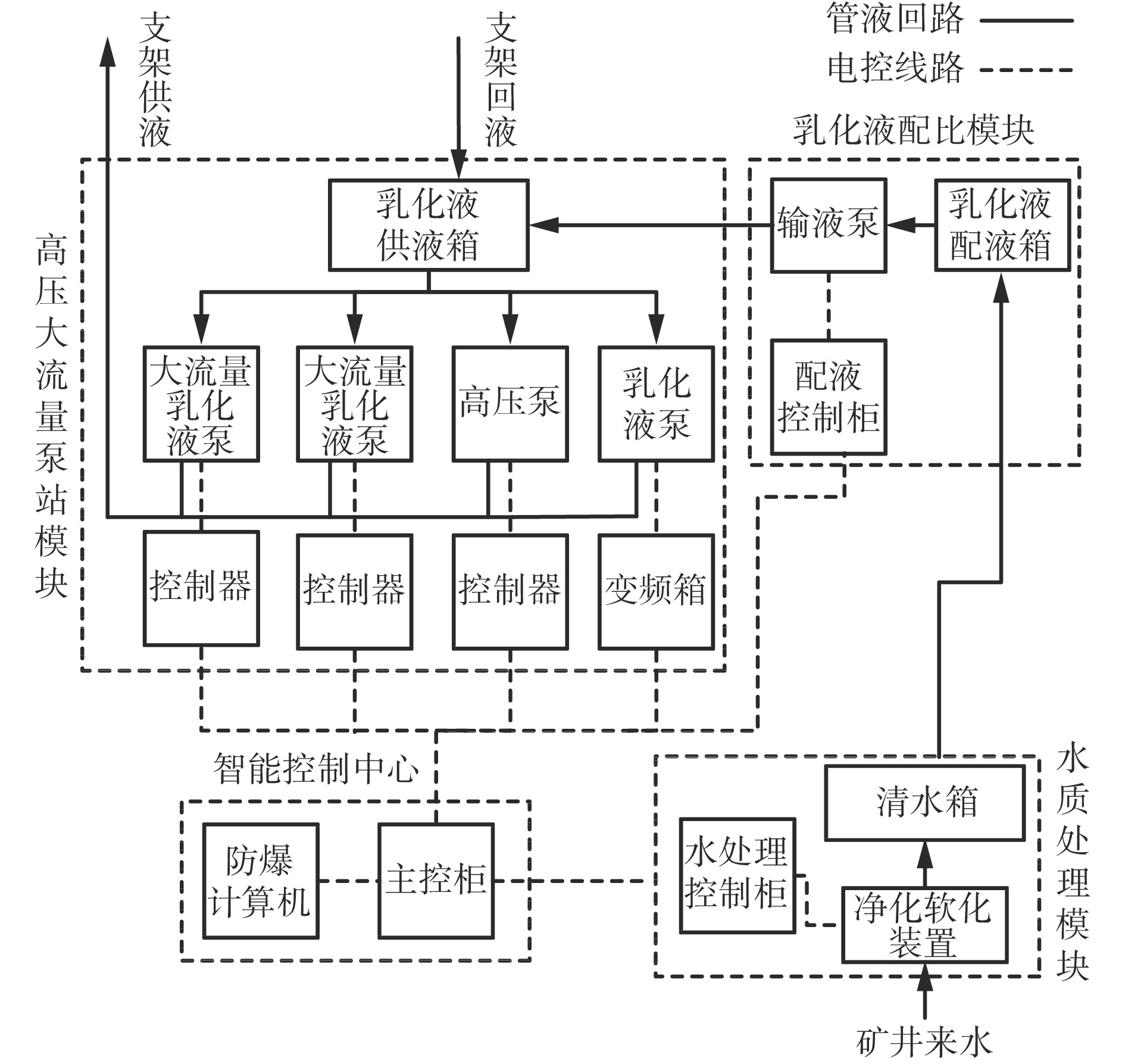
供液系统主要由智能控制中心、高压大流量泵站模块、乳化液配比模块、水质处理模块等组成，并通过电控线路和管液回路相互连接，如图1所示。智能控制中心通过输出智能策略控制高压大流量泵站模块执行乳化液输出决策，乳化液配比模块执行配比决策，水质处理模块执行净化软化水的决策。

图  1  供液系统结构

Figure  1.  Liquid supply system structure

下载: 全尺寸图片 幻灯片

高压大流量泵站由控制器、变频箱、乳化液供液箱、大流量乳化液泵、高压泵、乳化液泵等组成。当综采工作面用液时，先变频驱动乳化液泵进入工作状态，若不满足当前用液量，立即启动工频驱动大流量乳化液泵组进行供液。乳化液通过乳化液供液箱吸液口进入乳化液泵进行加压，随后由出液口向液压支架供液。高压泵用于提供大采高工作面高压初撑压力，智能控制中心向液压支架系统发送指令，使乳化液进入液压支架立柱下腔，从而将顶梁升起，当立柱下腔压力达到高压泵工作压力且顶梁上部接触到顶板后，高压泵自动卸载，液控单向阀关闭，使立柱下腔乳化液被封闭，完成液压支架的初撑阶段。

2.   乳化液泵近似模型

供液系统供液过程是个非常复杂的动态过程，支架动作时压力和流量的波动与系统总管压力、回液腔压力、支架负载阻力和液压流经管路、阀件等部件的压力损失等有关。智能控制中心输出控制信号到乳化液泵控制器，再由乳化液泵控制器控制乳化液泵输出流量，因此重点研究乳化液泵近似模型。

在乳化液泵给液压支架供液时，系统压力变换分为恒压和升压2个阶段，将变频器和异步电动机近似为时间常数为$ {T}_{1} $的一阶惯性环节，乳化液泵供液时恒压阶段压力保持不变，升压阶段为时间常数为$ {T}_{2} $的一阶惯性环节。系统其他环节（如变频器调节、压力检测等）的时间常数和滞后时间均可等效为比例环节。

乳化液泵的近似模型为

式中：G为传递函数；s为压力调节时间；$ {D}_{1} $为电动机速度增益；$ {D}_{2} $为供液系统增益；$ {D}_{3} $为压力传感器增益；$ \tau $为供液阶段滞后常数。

3.   IPSO−FNN−PID算法

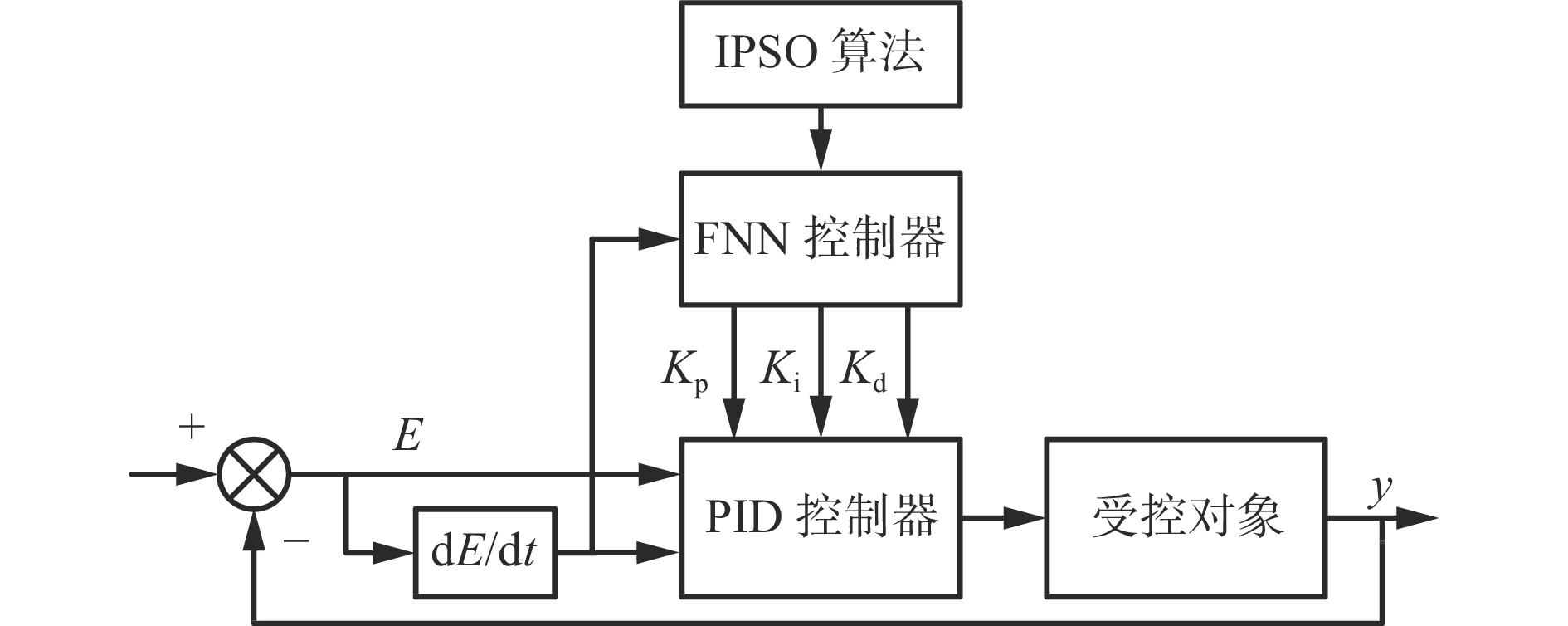
IPSO−FNN−PID控制器（图2）通过IPSO算法优化FNN参数，再利用BP神经网络算法的自适应特性对输入参数进行训练，调整输出最佳比例系数${K}_{{\rm{p}}}$、积分系数${K}_{{\rm{i}}}$、微分系数${K}_{{\rm{d}}}$，实现稳压供液。图2中E为压力偏差，t为时间，y为流量输出。

图  2  IPSO−FNN−PID控制器

Figure  2.  IPSO-FNN-PID controller

下载: 全尺寸图片 幻灯片

3.1   FNN

3.1.1   FNN结构

FNN结构采用节点数为3−7−7−3的4层神经网络结构。第1层为输入层，${K}_{{\rm{p}}0}$，${K}_{{\rm{i}}0}$，${K}_{{\rm{d}}0}$为FNN的3个输入量；第2层为模糊层，模糊层将输入变量进行模糊化处理，通过高斯函数表达输入变量的隶属度，调整该层的阈值和权值，更改高斯函数的中心向量和宽度向量，进一步获取不同位置、形状的隶属函数；第3层为模糊推理层，将第2层得到的隶属度两两相乘，得到模糊规则的规则强度，再根据划分的模糊子集确定模糊规则；第4层为输出层，将优化后的参数${K}_{{\rm{p}}}$，${K}_{{\rm{i}}}$，${K}_{{\rm{d}}}$输出。

3.1.2   隶属度函数

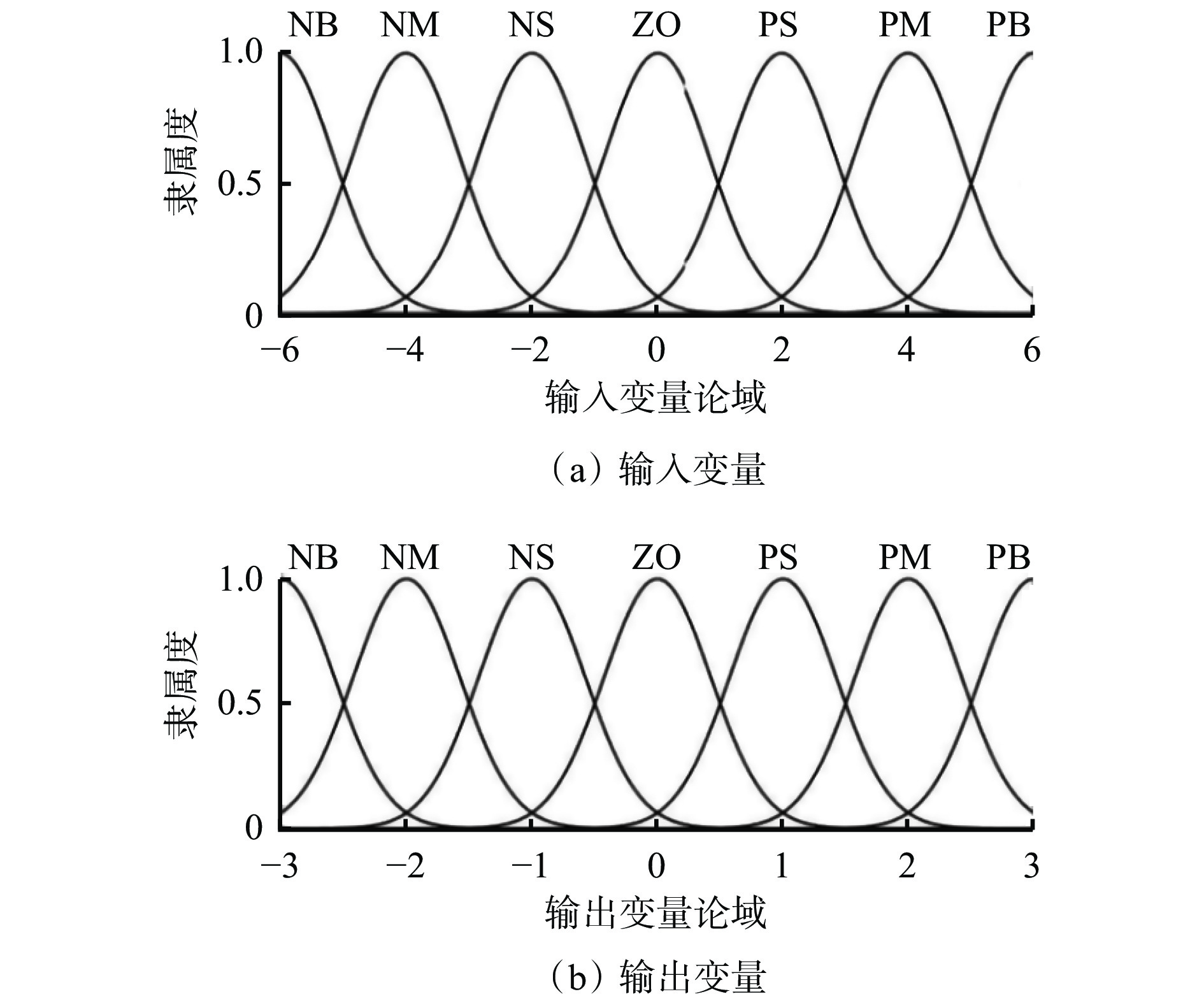
以当前压力偏差E、偏差的变化率E_C作为输入变量，设定E、E_C及输出变量U的7个模糊子集为{负大，负中，负小，零，正小，正中，正大}，简记为{NB，NM，NS，ZO，PS，PM，PB}。使用高斯函数作为隶属度函数，量化级分别为[−6, 6]，[−3, 3]，E_C和U的隶属度函数曲线如图3所示。可看出当输入/输出变量在论域中变动时，输入/输出变量的隶属度越接近于1，表示输入/输出变量属于对应模糊集的程度越高。

图  3  输入变量和输出变量的隶属度函数曲线

Figure  3.  Membership function curves of input and output variable

下载: 全尺寸图片 幻灯片

3.1.3   模糊规则

根据系统输入特性，以消除压力偏差为目的，根据管理人员的日常经验及相应准则，归纳整理成模糊规则库，见表1。

表  1  模糊控制规则

Table  1.  Fuzzy control rules

EC	E
	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PB	PM	PM	PS	PS	ZO
NM	PB	PM	PM	PS	PS	ZO	NS
NS	PM	PM	PS	PS	ZO	NS	NS
ZO	PM	PS	PS	ZO	NS	NS	NM
PS	PS	PS	ZO	NS	NS	NM	NM
PM	PS	ZO	NS	NS	NM	NM	NB
PB	ZO	NS	NS	NM	NM	NB	NB

下载: 导出CSV 

| 显示表格

3.1.4   激活函数

输入层及模糊推理层激活函数分别为

式中：$ {x}_{o} $为第o个输入变量，$ o=1，2，3 $；$ {w}_{oj} $为高斯函数中的第o个输入变量的第j个模糊集隶属度函数的均差，j=1，2，…，7；$ {\eta }_{oj} $为标准差。

将模糊化的输入变量进行两两相乘，得到模糊推理层的输出结果，激活函数为

式中N为模糊集个数。

${K}_{{\rm{p}}}$，${K}_{{\rm{i}}}$，${K}_{{\rm{d}}}$的输出为

式中$ \omega $为模糊推理层与输出层之间的连接权值。

3.2   IPSO算法

将PSO算法与IA相结合可保证粒子群的多元化，加入疫苗接种和良种选择2种算子，导入待求解问题的先验知识，可提升算法的全局收敛速度，有效避免陷入局部最优解。用算子优化粒子抗体种群H(n)（n为迭代次数）的流程如下：首先，呈递抗原，即输入目标函数和约束条件；其次，通过随机方法生成初始抗体种群，每个抗体为一个可行解，抗体种群$ H\left( 0 \right) = [ {h_1}\left( 0 \right),{h_2}\left( 0 \right), $…,${h_l}\left( 0 \right) ] $，l为粒子编号，l=1，2，…，m，m为粒子总个数；然后，进行疫苗抽取，通过处理问题经验，抽取抗体内分量的经验特征；最后，通过适配值衡量抗原与抗体的适应度，判断是否达到粒子群收敛目标，如未达到粒子群收敛目标，则进行疫苗接种，生成种群Y(n)，进一步通过良种选择生成种群Z(n+1)，再进行适配值计算，判断是否达到收敛目标，依此往复循环，直到粒子群达到收敛目标，算法结束。

为验证IPSO算法的有效性，在供液过程中选取800组数据作为训练集，IPSO−FNN算法的初始参数：单个粒子群规模为60，粒子群维数为6，最大迭代次数为400。

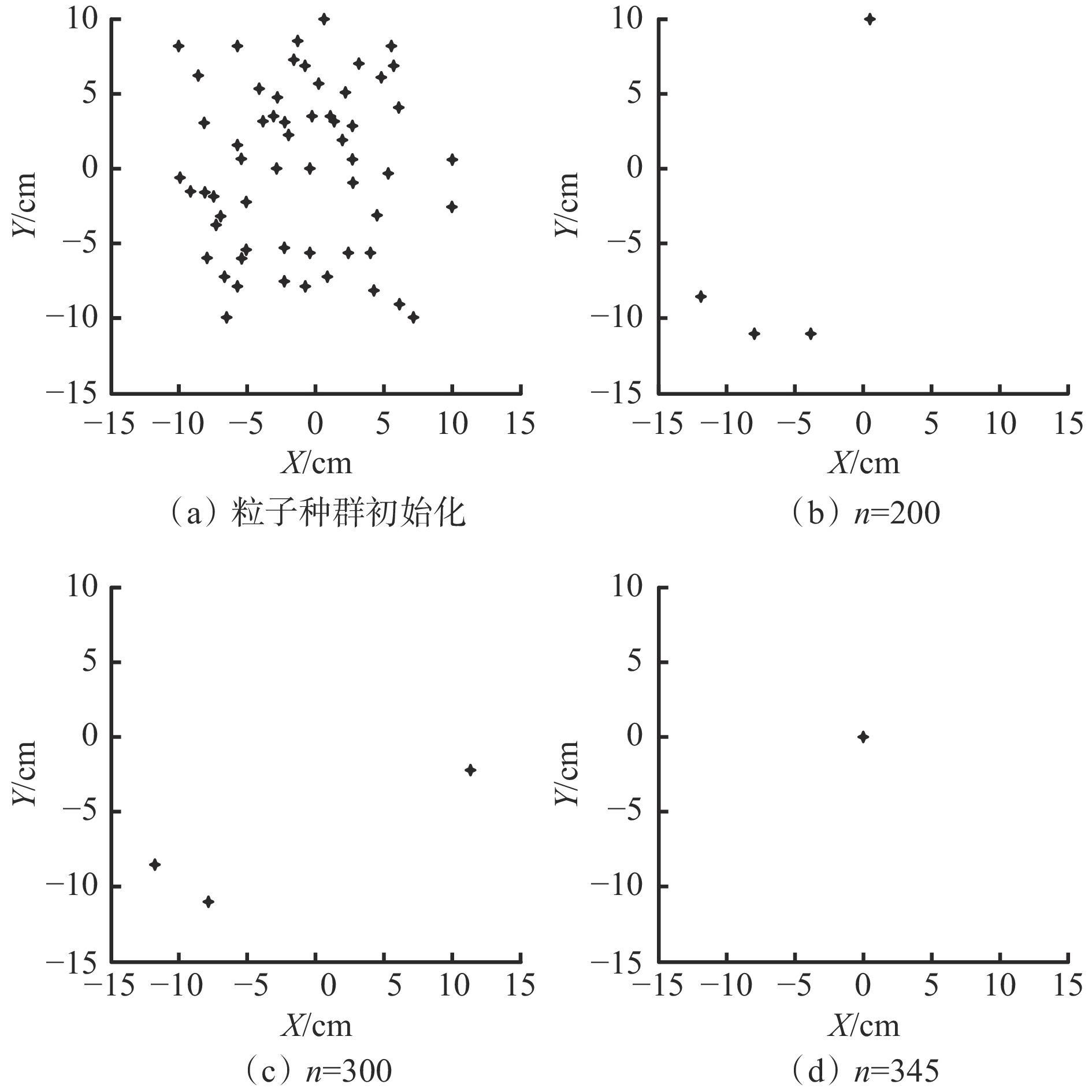
IPSO算法寻优粒子位置如图4所示，(X, Y)为粒子位置坐标。可看出 IPSO算法并无早熟现象，且当迭代次数n为345时，IPSO算法将所有粒子推向全局最优点。

图  4  IPSO算法粒子寻优位置

Figure  4.  IPSO algorithm particle optimization position

下载: 全尺寸图片 幻灯片

3.3   IPSO−FNN算法

通过IPSO算法对标准差$ {\eta }_{oj} $、均差$ {w}_{oj} $和连接权值$ \omega $进行优化。

设粒子群的粒子数量为Q，将待优化参数看作每个粒子的位置$ {a}_{k}^{l} $，按行展开可得$ {a}_{k}^{l} $=（$ {\eta }_{11} $，$ {\eta }_{12} $，…，$ {\eta }_{lk} $，$ {w}_{11} $，$ {w}_{12} $，…，$ {w}_{lk} $，$ {\omega }_{11} $，$ {\omega }_{12} $，…，$ {\omega }_{lk} $），k为r维向量第k个分量，$ k=\mathrm{1,2}, $… ,7， IPSO−FNN算法步骤如下。

（1） 对模糊神经网络进行初始化操作。确定模糊神经网络连接权值$ \omega $、输入输出训练样本集、标准差${\eta }_{{o}{j}}$和均差$ {w}_{oj} $。

（2） 对粒子群算法进行初始化操作并开始寻优。

（3） 通过适应度函数对当前进化代中每个粒子的最优位置$ {q}_{k}\left(n\right) $和迭代过程中每个粒子的最优位置$ {q}_{k}^{l}\left(n\right) $进行评价。

式中：J为粒子适应度值；$ {y}_{zl} $为第l个粒子第z个输出节点的期望输出值；$ {\hat{y}}_{zl} $为第l个粒子第z个输出节点的实际输出值。

（4） 衡量粒子多样性。若第n代粒子的多样性程度div(n)小于设定值δ，说明粒子需要免疫算法来增强多样性，此时进入免疫算法部分；若div(n)大于设定值δ，则转入下一步。

式中$ {p}_{b}\left(n\right) $为第n代第b个粒子良种选择概率。

（5） 更新粒子群参数，判断最大迭代数，若达到最大迭代数，则输出$ {q}_{k}^{l}\left(n\right) $，否则转入步骤（3），直到找到全局最优解。

4.   仿真与结果分析

4.1   控制器阶跃响应性能验证

为验证IPSO−FNN−PID控制器在控制效果上的优势，选取传统PID控制器、Fuzzy−PID控制器、FNN−PID控制器作为对照组，在Matlab-Simulink软件中进行仿真。通过对数据的拟合整理，确定电动机速度增益D_1、供液系统增益$ {D}_{2} $及压力传感器增益$ {D}_{3} $三者乘积为$ D=10 $，电动机的时间常数$ {T}_{1} $与升压阶段时间常数$ {T}_{2} $的乘积为11，$ {T}_{1} $与$ {T}_{2} $之和为60，供液阶段滞后常数$ \tau $=2$ ， $将上述值代入式（1），可得

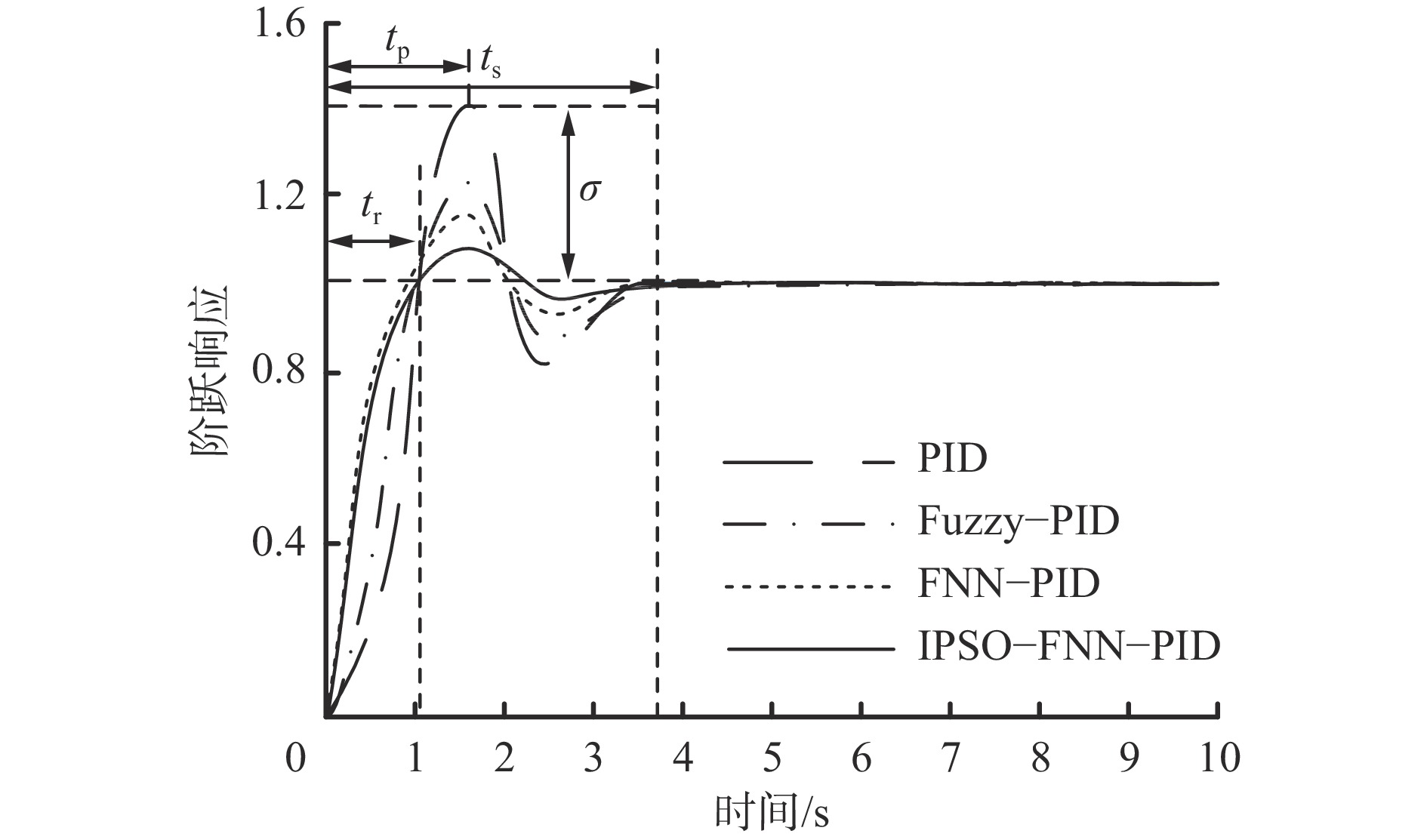
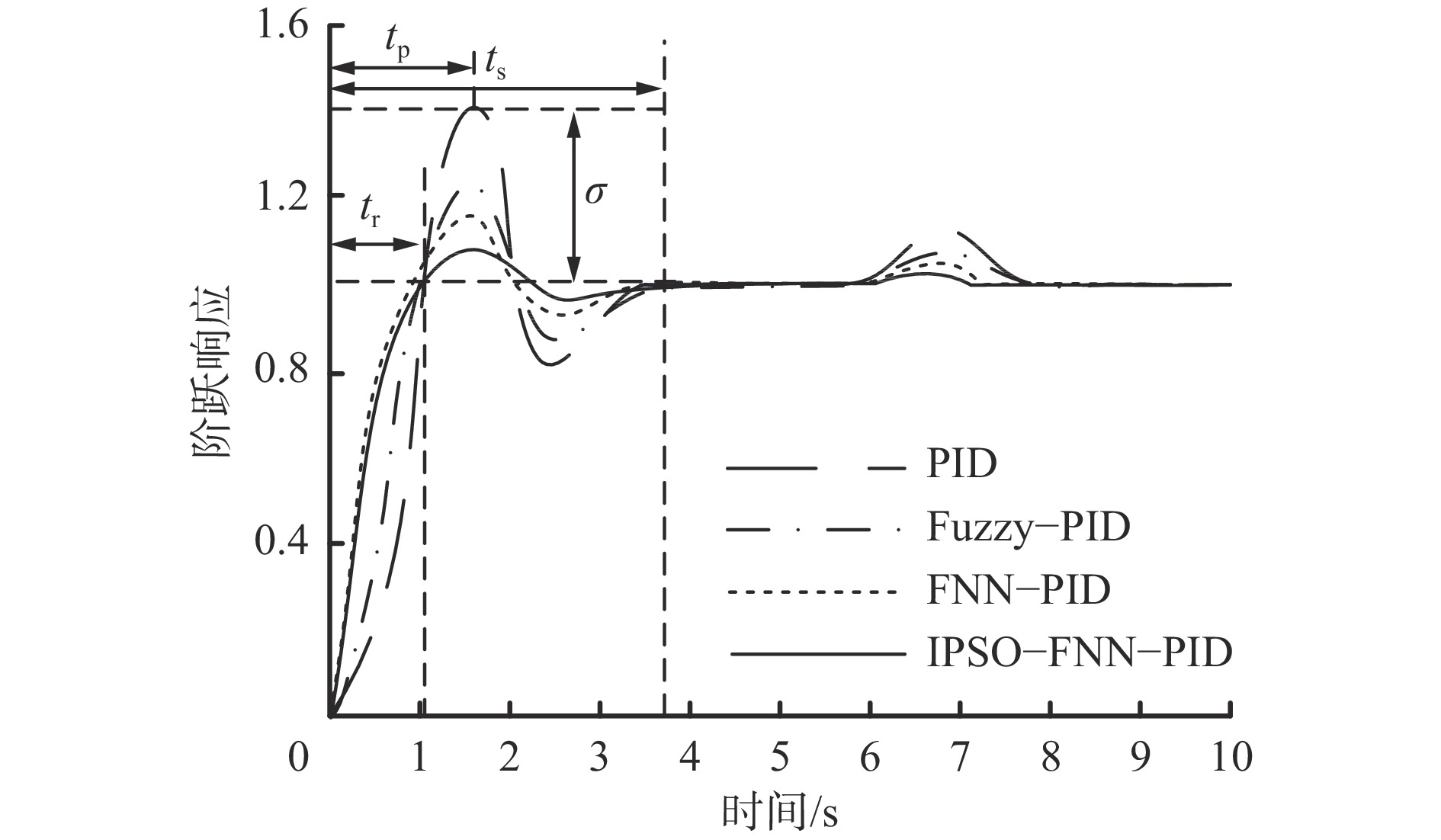
PID的3个输出参数${K}_{{\rm{p}}}$=3.215，${K}_{{\rm{i}}}$=4.583，${K}_{{\rm{d}}}$=4.112，模糊PID的3个输出参数通过模糊规则进行修正，FNN算法、IPSO−FNN算法均采用反向传播标准梯度下降法进行训练，各控制器的阶跃响应曲线如图5所示。可看出IPSO−FNN−PID控制器对乳化液泵的控制效果最佳，其他3种控制器的上升时间${t}_{{\rm{r}}}$、峰值时间${t}_{{\rm{p}}}$及调节时间${t}_{{\rm{s}}}$比IPSO−FNN−PID控制器长，最大超调量$ \mathrm{\sigma } $均大于IPSO−FNN−PID控制器。

图  5  各控制器阶跃响应曲线

Figure  5.  Step response curve of each controller

下载: 全尺寸图片 幻灯片

在实际工作环境中，供液流量会受到未知条件干扰和影响，为了验证IPSO−FNN−PID控制器的鲁棒性，在系统运行6 s时给4种控制器加入扰动，4种控制器的扰动仿真结果如图6所示。可看出在加入扰动信号后，IPSO−FNN−PID控制器具有较好的自适应性和鲁棒性，恢复到平稳状态仅用了1.2 s，能及时地起到控制作用。

图  6  各控制器扰动仿真结果

Figure  6.  Disturbance simulation results of each controller

下载: 全尺寸图片 幻灯片

4.2   控制器动态性能验证

各算法PID控制参数包括：${K}_{{\rm{p}}}$，${K}_{{\rm{i}}}$，${K}_{{\rm{d}}}$，动态性能指标包括最大超调量$ \mathrm{\sigma } $、上升时间${t}_{{\rm{r}}}$、峰值时间${t}_{{\rm{p}}}$及调节时间${t}_{{\rm{s}}}$，见表2。

表  2  各控制器PID控制参数及动态特性比较

Table  2.  Comparison of PID control parameters and dynamic characteristics of each controller

控制器	${K}_{{\rm{p}}}$	${K}_{{\rm{i}}}$	${K}_{{\rm{d}}}$	$ \mathrm{\sigma } $/%	${t}_{{\rm{r}}}$/s	${t}_{{\rm{p}}}$/s	${t}_{{\rm{s}}}$/s
PID	3.215	4.583	4.112	41.2	1.01	1.71	3.72
Fuzzy−PID	0.691	2.892	3.672	22.3	1.34	1.63	3.56
FNN−PID	0.882	3.000	3.127	17.6	0.98	1.55	2.68
IPSO−FNN−PID	1.218	2.614	3.745	5.22	0.89	1.31	2.61

下载: 导出CSV 

| 显示表格

由表2可得：

(1) 采用传统PID控制器对乳化液泵进行控制时，振荡幅度明显，调节时间过长且最大超调量达41.2%，在受到外界干扰情况下，振荡幅度较大且收敛较慢。

(2) 采用Fuzzy−PID控制器对乳化液泵进行控制时，最大超调量为22.3%，在受到扰动信号干扰时，振荡虽略有减弱，但趋于平缓时间与传统PID控制器趋于平缓时间基本相同，所以采用模糊PID控制器依旧存在很大问题。

(3) 采用FNN−PID控制器对乳化液泵进行控制时，调节时间缩短至2.68 s，这是因为在FNN−PID控制器中加入了模糊控制的过程，导致控制精度增加，但同时增加了计算量和网络的复杂度，在接收到扰动信号时，振荡明显减弱，收敛速度也略有提升。

(4) 采用IPSO−FNN−PID控制器对乳化液泵进行控制时，系统的最大超调量为5.22%，曲线接近理想状态，几乎无振荡，调节时间为2.61 s，系统很快进入稳定状态。这是因为在IPSO−FNN−PID控制器中加入了模糊控制及IA，保证了粒子的多样性，同时引入疫苗接种和良种选择2种算子，进而导入待求解问题的先验知识，可提升算法的全局收敛速度，避免了模糊过程中带来的冗余计算量，加快了网络收敛速度，可尽快抑制系统的超调量。在受到扰动信号时，负载干扰对IPSO−FNN−PID控制器的影响较小，且控制器收敛迅速，鲁棒性大大提升，表明IPSO−FNN−PID控制器具备良好的抗扰动及扰动补偿能力，可满足供液系统的稳压控制要求。

5.   结论

（1） 为了更好满足综采工作面供液系统的控制需求，提出了一种IPSO−FNN−PID算法。针对FNN算法易陷入局部寻优问题，引入PSO算法，同时在PSO算法中加入IA的疫苗接种和良种选择2种算子，通过疫苗接种生成种群Y(n)，进一步通过良种选择生成Z(n+1)代种群，以提高PSO算法的收敛性，达到优化FNN算法的目的，实现最优${{K}}_{{{\rm{p}}}}$，${{K}}_{{{\rm{i}}}}$，${{K}}_{{{\rm{d}}}}$参数输出。

（2） IPSO−FNN−PID控制器对乳化液泵的控制效果最佳，PID，Fuzzy−PID，FNN−PID控制器的上升时间、峰值时间和调节时间比IPSO−FNN−PID控制器长，最大超调量均大于IPSO−FNN−PID控制器。

（3） 以乳化液泵的数学模型作为控制对象，在系统运行6 s时给PID，Fuzzy−PID，FNN−PID和IPSO−FNN−PID 控制器加入扰动，IPSO−FNN−PID控制器具有更好的自适应性和鲁棒性，恢复到平稳状态仅用了1.2 s，能及时地起到控制作用。

（4） 采用IPSO−FNN−PID控制器对乳化液泵进行控制时，几乎无振荡，超调量仅为5.22%，调节时间缩短至2.61 s，遇到干扰信号时稳定性更强，且收敛迅速，鲁棒性大大提升，表明IPSO−FNN−PID控制器具备良好的抗扰动及扰动补偿能力，可满足供液系统的稳压控制要求。