Dynamic weighing method for coal and gangue in coal-gangue sorting robots
-
摘要:
基于图像识别的煤矸分拣机器人是煤矸分拣领域的研究热点。针对实际复杂工况下煤矸图像易受灰尘附着、光照变化、水渍粘黏、煤泥水覆盖等因素影响而导致煤矸识别准确率低的问题,提出了一种融合拉力传感器和加速度传感器的煤矸动态称重方法,以实现煤矸二次识别。通过分析煤矸分拣机器人机械臂高速运动过程中三轴加速度对拉力传感器的影响机理,建立了基于三轴加速度补偿的煤矸动态称重模型;进一步引入四分位距(IQR)算法构建异常值剔除机制,以抑制动态称重模型中的随机噪声。搭建了煤矸分拣机器人的煤矸动态称重实验平台进行实验,结果表明:未融合三轴加速度补偿时称重误差达66.43%,引入z轴和x,y轴加速度补偿后误差分别降至12.97%,8.69%,加入IQR算法后的煤矸动态称重模型的称重误差进一步降至4.69%,较未融合三轴加速度补偿和IQR算法时降低了61.74%;该模型能对密度差异大于0.35 g/cm3的煤和矸石实施二次识别,有效解决了实际复杂工况下煤矸识别准确率过低的问题。
Abstract:Image recognition-based coal-gangue sorting robots have become a research hotspot in the field of coal-gangue separation. To address the issue of low recognition accuracy caused by complex real-world conditions—such as dust adhesion, lighting variation, water stains, and coal slurry coverage—a dynamic weighing method for coal and gangue was proposed, integrating a tension sensor and an acceleration sensor to enable secondary recognition. By analyzing the influence mechanism of triaxial acceleration on the tension sensor during the high-speed motion of the robotic arm in a coal-gangue sorting robot, a dynamic weighing model for coal and gangue based on triaxial acceleration compensation was established. Furthermore, an outlier elimination mechanism based on the interquartile range (IQR) algorithm was introduced to suppress random noise in the dynamic weighing model. An experimental platform for dynamic weighing of coal and gangue in a coal-gangue sorting robot was constructed to conduct experiments. Experimental results showed that the weighing error reached 66.43% without triaxial acceleration compensation. After introducing z-axis, and x-and y-axis acceleration compensation, the errors were reduced to 12.97% and 8.69%, respectively. With the addition of the IQR algorithm, the weighing error of the dynamic weighing model was further reduced to 4.69%, representing a 61.74% reduction compared to the case without triaxial acceleration compensation and the IQR algorithm. The model was able to achieve secondary recognition between coal and gangue when their density difference exceeded 0.35 g/cm3, effectively solving the problem of low recognition accuracy under complex real-world conditions.
-
0. 引言
煤矸分选是原煤生产过程中的关键环节之一[1-2],目前常用基于图像识别[3]、X射线探测[4]、热红外响应分析[5]、高光谱成像[6]、激光反射率检测[7]等方法实现煤与矸石的有效识别。其中基于图像识别的煤矸分拣机器人已成为当前煤矸分拣领域的研究热点[8-10]。但在实际工况下,受灰尘附着、光照变化、水渍粘黏、煤泥水覆盖等外界因素的影响,仅采用图像特征难以完成煤与矸石的准确识别。因此,可在煤矸图像特征的基础上引入煤矸密度特征,利用煤矸的密度差异进行煤矸二次识别,以提高实际工况下的煤矸识别准确率。
动态称重作为一种能够在运动状态下采集目标质量信息的技术手段,是获取煤矸密度特征的关键环节。按照参与动态称重传感器的类型,可将其分为两类:① 通过分析单一传感器采集数据完成指定目标的称重。② 融合多个传感器采集的数据,通过动态补偿完成指定目标的称重。针对基于单一传感器的动态称重方法,Zhang Chen等[11]通过在胶带末端安装称重平台,对滑落煤矸进行动态质量检测,采用均值滤波法处理动态称重信号以获取煤矸质量,并基于密度特征开发了煤矸分选系统,煤矸分选精度达到60%;袁娜[12]通过分析机械臂抓取煤矸的过程,选择可稳态测量煤矸质量的阶段,利用安装于机械臂上的拉力传感器实现了煤矸动态称重,称重误差为5.74%;Zhang Zhen等[13]提出了一种基于柔性压力传感器的机器人手爪称重系统,采用多项式拟合算法建立了柔性压力传感器输出与被称重目标真实质量之间的映射关系,并通过实验得到了二次多项式拟合效果最优的结论。针对多传感器融合的动态称重方法,A. Kosiara等[14]通过融合油压传感器和倾斜传感器,建立了挖掘机铲斗的动态称重模型,可在1个典型工作周期内估算铲斗内物料的质量,相对误差小于5%;李达等[15]采用BP神经网络处理4路压力传感器信号,并使用粒子群优化(Particle Swarm Optimization, PSO)算法优化BP神经网络的权值及阈值,其动态称重的平均相对误差小于5.3%;王秦越等[16]提出了一种基于扩展卡尔曼滤波算法的动态称重方法,利用多传感器融合技术有效抑制了干扰噪声对测量系统的影响,提高了动态称重精度;章玉等[17]将三轴加速度与动态质量信号进行低通滤波处理后输入PSO−径向基函数(Radial Basis Function,RBF)模型进行质量预测,使胶带伸缩机上包裹在传输过程中的称重误差减小至0.9%。
基于单一传感器的动态称重方法因数据维度有限,对动态环境的适应性较差,而多传感器融合方法通过多源信号协同处理,可有效提高动态称重的精度及稳定性。因此,本文在顺应现有煤矸分拣机器人分拣工艺的基础上,借鉴多传感器融合的动态称重方法,提出一种面向煤矸二次识别系统的煤矸动态称重方法。通过分析动态场景下拉力传感器的工作特性,采用三轴加速度动态补偿因机械臂加减速运动引起的煤矸称重误差,并结合四分位距(Inter Quartile Range,IQR)算法剔除动态称重过程中的随机噪声,实现了煤矸二次识别系统中煤矸质量的在线准确获取。
1. 问题描述
1.1 煤矸二次识别系统
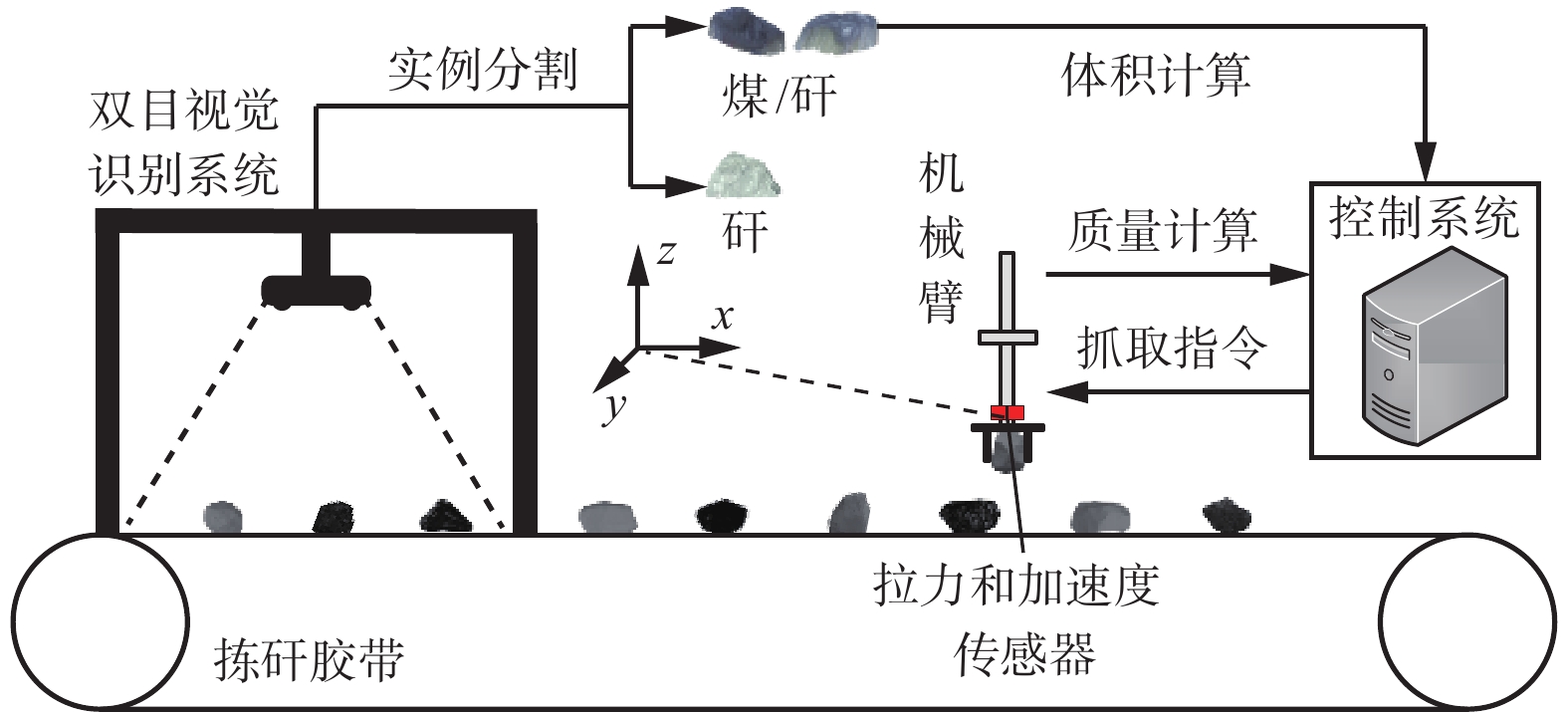
煤矸二次识别系统由拣矸胶带、双目视觉识别系统、机械臂、控制系统组成,如图1所示。煤和矸石由拣矸胶带运输。首先,由实例分割模型完成所有煤和矸石的检测与分割[18],输出煤矸图像识别结果和分割后的煤矸点云,完成煤矸一次识别。然后,将一次识别结果中置信度较低的煤矸确定为二次识别目标,同时利用双目视觉技术和机械臂动态称重方法获取目标的检测体积和检测质量。最后,控制系统结合目标检测体积和检测质量计算出目标检测密度,通过与预设的煤矸真实密度进行比较,实现煤矸二次识别,若目标被判断为煤则中断抓取过程,将煤放回胶带,否则继续抓取过程,完成煤矸分拣。
1.2 煤矸动态称重
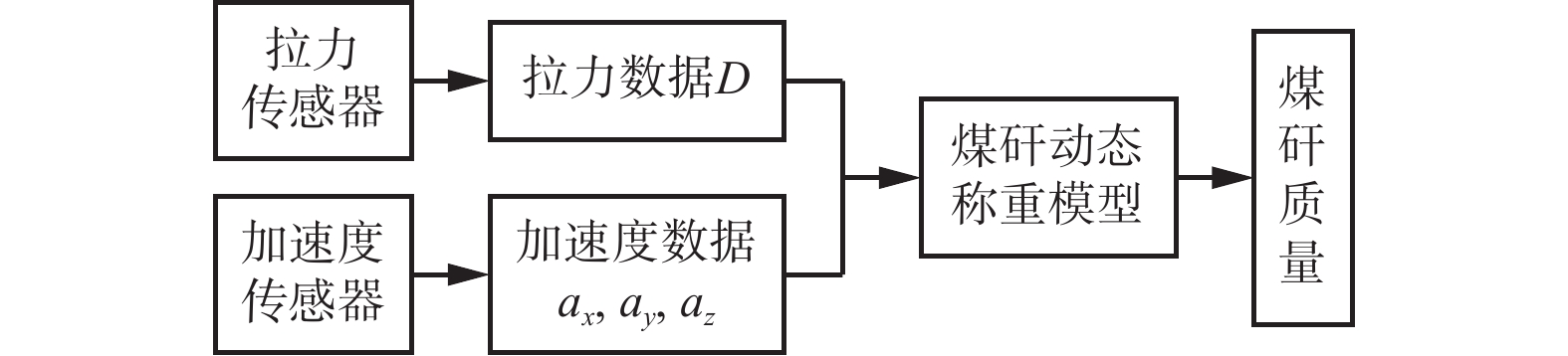
为减少煤矸动态称重过程中机械臂加减速对目标煤矸质量测量结果的影响,将拉力传感器和加速度传感器安装于机械臂上,通过融合机械臂抓取煤矸过程中的拉力和加速度数据,实现煤矸质量的动态获取,如图2所示。
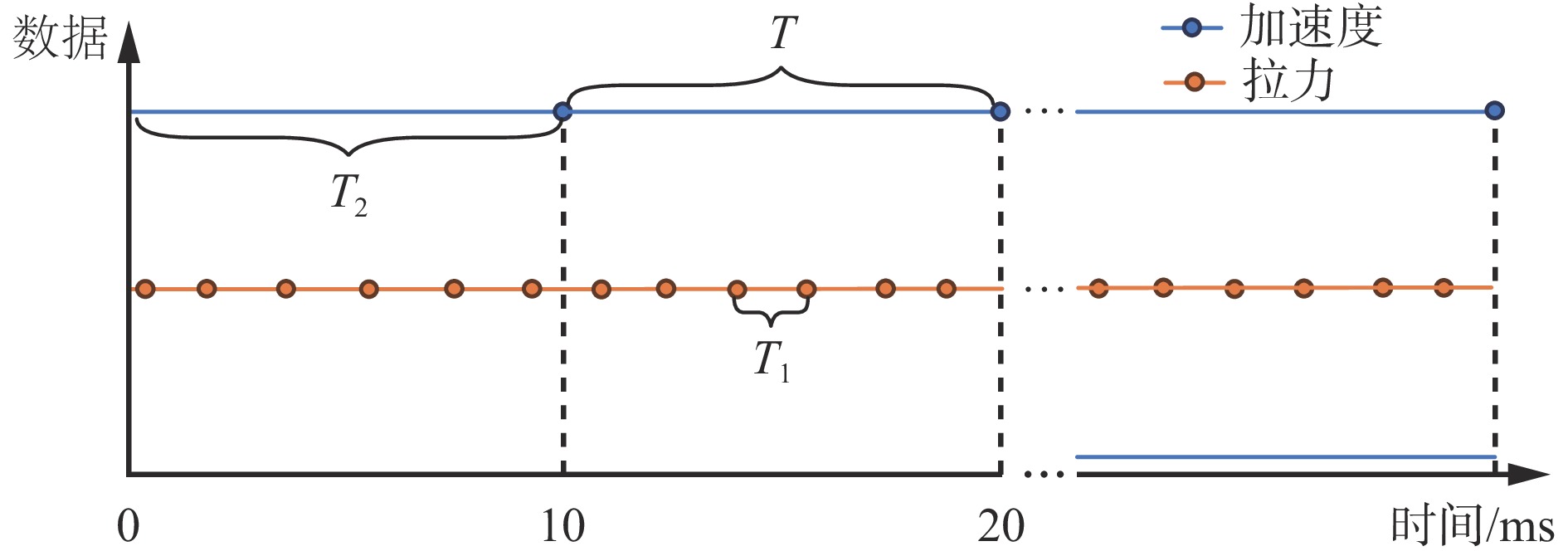
由于采用了多传感器融合方案进行动态称重,所以需考虑拉力传感器和加速度传感器之间的数据对齐问题。已知拉力传感器和加速度传感器的采样周期分别为1.56,10 ms,选择加速度传感器的采样周期10 ms作为动态称重的数据采集周期,以实现传感器数据对齐。传感器数据对齐方案如图3所示。T为称重数据采集周期,T1,T2分别为拉力传感器和加速度传感器的采样周期。
2. 拉力传感器工作特性分析
定义胶带运行方向为x轴,胶带宽度方向为y轴,煤矸分拣机器人抓取矸石方向为z轴,分析拉力传感器在三轴方向上的力电转换关系。
2.1 沿z轴方向的力电转换关系
当沿z轴力Fz作用于拉力传感器测力轴线上时,Fz与拉力传感器输出电压U之间的线性关系为
Fz=kzU+bz (1) 式中kz,bz为待定参数,可通过待定系数法确定。
U可由拉力传感器输出的数字量表示,即
U=Umax (2) 式中:Umax为传感器满量程时的输出电压,为10 V;Dmax为AD芯片能输出的最大数字量,本文中AD芯片为24位,则Dmax=224−1=16 777 215;D为传感器输出的数字量。
将式(1)与式(2)联立,得到拉力传感器沿z轴的力电转换关系:
F_{\textit{z}} = k_{\textit{z}} \frac{U_{\max}}{D_{\max}}D + b_{\textit{z}} (3) 沿拉力传感器的测力轴线(即z轴方向)施加标准载荷,记录传感器输出的数字量D,采用最小二乘法得kz = 54.571 0,bz = −1.648 5。相关数据见表1。
表 1 z轴载荷与传感器输出值Table 1. z-axis load and sensor output valuesFz/N 50 100 150 ··· 400 D 1 596 472 3 092 938 4 685 316 ··· 1 2361 424 2.2 沿x,y轴方向的力电转换关系
理想情况下,拉力传感器仅对沿测力轴线方向的力敏感,但实际情况下由于拉力传感器存在交叉灵敏度,表现为当沿拉力传感器的测力轴线法向施加拉力时,传感器也会存在信号输出,且输出信号与所施加的力呈正比[19]。因此,沿测力轴线法向施加的载荷Fx或Fy与传感器输出电压U之间的关系为
F_x = k_x U + b_x (4) F_y = k_y U + b_y (5) 式中kx,ky,bx,by为未知参数。
将式(4)和式(5)分别与式(2)联立,可知拉力传感器沿x,y轴的力电转换关系:
F_x = k_x \frac{U_{\max}}{D_{\max}}D + b_x (6) F_y = k_y \frac{U_{\max}}{D_{\max}}D + b_y (7) 沿x轴和y轴分别施加标准载荷,同时记录传感器输出的数字量D,采用最小二乘法可得kx = 1 702.345 0,ky = 1 856.394 2,bx = −1.271 4,by = −1.040 3。相关数据见表2、表3。
表 2 x轴载荷与传感器输出值Table 2. x-axis load and sensor output valuesFx/N 10 30 50 ··· 200 D 11 027 30 770 50 513 ··· 198 588 表 3 y轴载荷与传感器输出值Table 3. y-axis load and sensor output valuesFy/N 10 30 50 ··· 200 D 9 968 28 355 45 786 ··· 181 967 3. 煤矸动态称重数学模型
在煤矸分拣机器人分拣煤矸过程中,拉力传感器除受到z轴(测力轴线)上的载荷Fz外,还会受到x,y轴(非测力轴线)上的载荷Fx,Fy。由于传感器交叉灵敏度的存在,会导致Fx,Fy在测力轴线方向产生寄生载荷[20],在构建动态称重模型时须考虑寄生载荷对称重结果的影响。由拉力传感器工作特性分析结果可知,三轴所受寄生载荷Fx,Fy,Fz与相应方向上传感器输出值分量Dx,Dy,Dz间的关系分别为
F_x = k_x \frac{U_{\max}}{D_{\max}}D_x + b_x (8) F_y = k_y \frac{U_{\max}}{D_{\max}}D_y + b_y (9) F_{\textit{z}} = k_{\textit{z}} \frac{U_{\max}}{D_{\max}}D_{\textit{z}} + b_{\textit{z}} (10) 拉力传感器的实际读数D由沿测力轴线方向载荷贡献的传感器读数Dz、非测力轴线方向载荷带来的寄生载荷贡献的传感器读数Dx和Dy共同组成。
D = D_x + D_y + D_{\textit{z}} (11) 对拉力传感器下方的整体进行动力学分析,根据牛顿第二定律,x,y,z三轴方向的载荷可表示为
F_x = (M_{\mathrm{g}} + M_{\mathrm{j}})a_x (12) F_y = (M_{\mathrm{g}} + M_{\mathrm{j}})a_y (13) F_{\textit{z}} = (M_{\mathrm{g}} + M_{\mathrm{j}})a_{\textit{z}} (14) 式中:Mg为被抓取煤矸质量;Mj为拉力传感器下方机械爪的质量;ax,ay,az分别为机械臂沿x,y,z三轴的加速度。
将式(8)—式(14)联立,可得煤矸质量Mg与拉力传感器读数D及三轴加速度ax,ay,az之间的关系:
M_{\mathrm{g}} = \left|\frac{\dfrac{U_{\max}}{D_{\max}}D + \left(\dfrac{b_x}{k_x} + \dfrac{b_y}{k_y} + \dfrac{b_{\textit{z}}}{k_{\textit{z}}}\right)}{\dfrac{|a_x|}{k_x} + \dfrac{|a_y|}{k_y} + \dfrac{a_{\textit{z}}}{k_{\textit{z}}}} - M_{\mathrm{j}}\right| (15) 由于寄生载荷大小与x,y轴加速度的方向无关,所以ax,ay在式(15)中取绝对值。
令k1=1/kx,k2=1/ky,k3=1/kz,c=Umax/Dmax,b=bx/kx+by/ky+bz/kz,则融合三轴加速度的煤矸质量计算公式可简化为
M_{\mathrm{g}} = \left|\frac{cD + b}{k_1\left|a_x\right| + k_2\left|a_y\right| + k_3a_{\textit{z}}} - M_{\mathrm{j}}\right| (16) 本文中Mj=9.388,k1=5.874 2×10−4,k2=5.386 8×10−4,k3=1.832 5×10−2,c=5.960 5×10−7,b=−3.151 6×10−2,代入式(16)可得
{M_{\mathrm{g}}} = \left| {\frac{{5.960\;5 \times {{10}^{ - 3}}D - 315.16}}{{5.874\;2\left| {{a_x}} \right| + 5.386\;8\left| {{a_y}} \right| + 183.25{a_{\textit{z}}}}} - 9.388} \right| (17) 当动态称重系统某时刻的拉力及加速度数据已知时,可使用式(17)得到煤矸质量的观测值,但一个质量观测值可能受随机误差或瞬时扰动的影响,难以表征煤矸的真实质量。因此,在机械臂抓取煤矸阶段采集多组拉力及加速度数据,计算出多组煤矸质量观测值,将其构成质量观测值集合S,然后采用统计学方法从S中分析出煤矸真实质量的估计值Mg。质量观测值集合S可表示为
S = \{M_{\mathrm{g}}(1), M_{\mathrm{g}}(2), \cdots, M_{\mathrm{g}}(n), \cdots, M_{\mathrm{g}}(N)\} (18) 式中:Mg(n)为通过第n组传感器数据计算出的煤矸质量;N为采集到的传感器数据组数。
由于传感器数据噪声的存在,集合S中不可避免地存在部分异常值,所以采用IQR算法寻找和剔除集合S中的异常值[21-22]。处理后的煤矸质量观测值集合可表示为
{S_{ 0}} = \{ {X_i}|{X_i} \in [{S_{ {\mathrm{Q}}1}} - 1.5 {S_{ {\mathrm{IQR}}}},{S_{ {\mathrm{Q}}3}} + 1.5 {S_{ {\mathrm{IQR}}}}]\} (19) 式中:Xi为集合S0中第i个煤矸质量观测值;SQ1为集合S的下四分位数;SIQR为集合S的IQR;SQ3为集合S的上四分位数。
剔除异常值后集合S0中元素的取值较为平均,可近似为均匀分布,因此计算其均值作为煤矸质量的估计值:
{M_{\mathrm{e}}} = {{\sum\limits_{i = 0}^k {\frac{X_i}{k}} } } (20) 式中k为煤矸质量观测值集合S0中的元素个数。
4. 煤矸动态称重实验
4.1 实验平台
煤矸分拣机器人的煤矸动态称重实验平台由视觉识别模块、煤矸分拣机器人本体和动态称重模块组成,如图4所示。视觉识别模块负责煤矸的实例分割与体积计算;煤矸分拣机器人本体负责追踪并抓取煤矸;动态称重模块负责采集煤矸被抓取过程的拉力及加速度数据,用于计算煤矸质量。平台可分拣的粒度范围为50~300 mm,运行过程中胶带速度恒定为0.5 m/s。
4.2 实验设计
为验证煤矸动态称重模型中加速度补偿机制及异常值处理算法存在的必要性,设计渐进式消融实验。实验对象选取陕西某矿区的煤矸样本,该样本中煤和矸石的真实平均密度分别为1.45,1.80 g/cm3。
通过逐步剥离完整动态称重模型的IQR异常值处理算法和x,y轴加速度补偿单元(ax, ay),z轴加速度补偿单元(az),构建4组实验对照:完整模型M1,移除IQR算法的模型M2,移除x,y轴加速度补偿的模型M3,移除三轴加速度补偿的模型M4。实验中称重误差为
{\varepsilon _{\mathrm{m}}} = \frac{{\left| {{M_{\mathrm{e}}} - {M_{\mathrm{t}}}} \right|}}{{{M_{\mathrm{t}}}}} \times 100{\text{%}} (21) 式中:Me为模型计算出的煤矸质量;Mt为煤矸真实质量,由标准电子秤在静态条件下采集。
4.3 实验结果
基于煤矸分拣机器人实验平台,按照上述实验设计进行实验,部分实验数据见表4。
表 4 动态称重实验结果Table 4. Dynamic weighing experiment results样本 真实质量/g 模型M1 模型M2 模型M3 模型M4 计算质量/g 误差/% 计算质量/g 误差/% 计算质量/g 误差/% 计算质量/g 误差/% 矸1 2 748 2 883 4.91 2 990 8.81 3 065 11.54 4 169 51.71 矸2 2 344 2 438 4.01 2 591 10.54 2 731 16.51 4 476 90.96 矸3 3 569 3 709 3.92 3 748 5.02 3 934 10.23 4 858 36.12 矸4 2 013 2 087 3.68 2 122 5.41 2 198 9.19 3 470 72.38 矸5 3 758 3 876 3.14 3 914 4.15 4 004 6.55 5 253 39.78 煤1 2 260 2 358 4.34 2 664 17.88 2 779 22.96 3 432 51.86 煤2 1 930 2 030 5.18 2 059 6.68 2 087 8.13 3 197 65.65 煤3 1 670 1 760 5.39 1 800 7.78 1 881 12.63 2 784 66.71 煤4 1 501 1 588 5.80 1 635 8.93 1 692 12.72 2 884 92.14 煤5 897 956 6.58 1 002 11.71 1 070 19.29 1 767 96.99 4.4 实验结果分析
4.4.1 定量分析
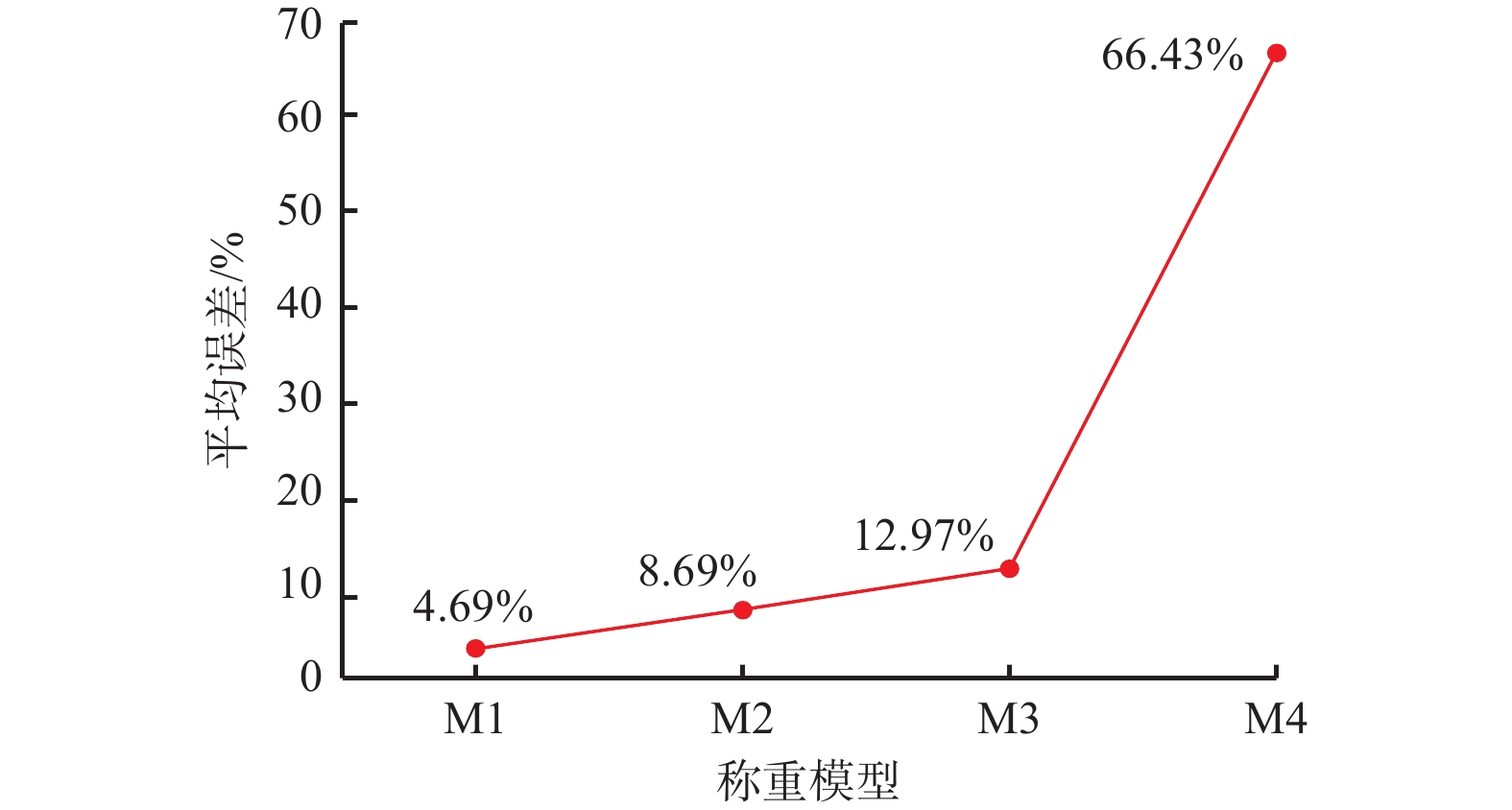
为定量分析加速度补偿机制及异常值处理算法对动态称重模型的影响,统计4个模型在计算多组样本质量时的平均误差,结果如图5所示。可看出完整模型M1动态称重的平均误差最低,为4.69%;移除IQR算法的模型M2平均误差较完整模型M1增大了4.00%;进一步移除x,y轴加速度补偿的模型M3的平均误差较完整模型M1增大了8.28%;移除三轴加速度补偿的模型M4的平均误差较完整模型M1增大了61.74%。因此,完整模型M1的动态称重精度最高。
4.4.2 定性分析
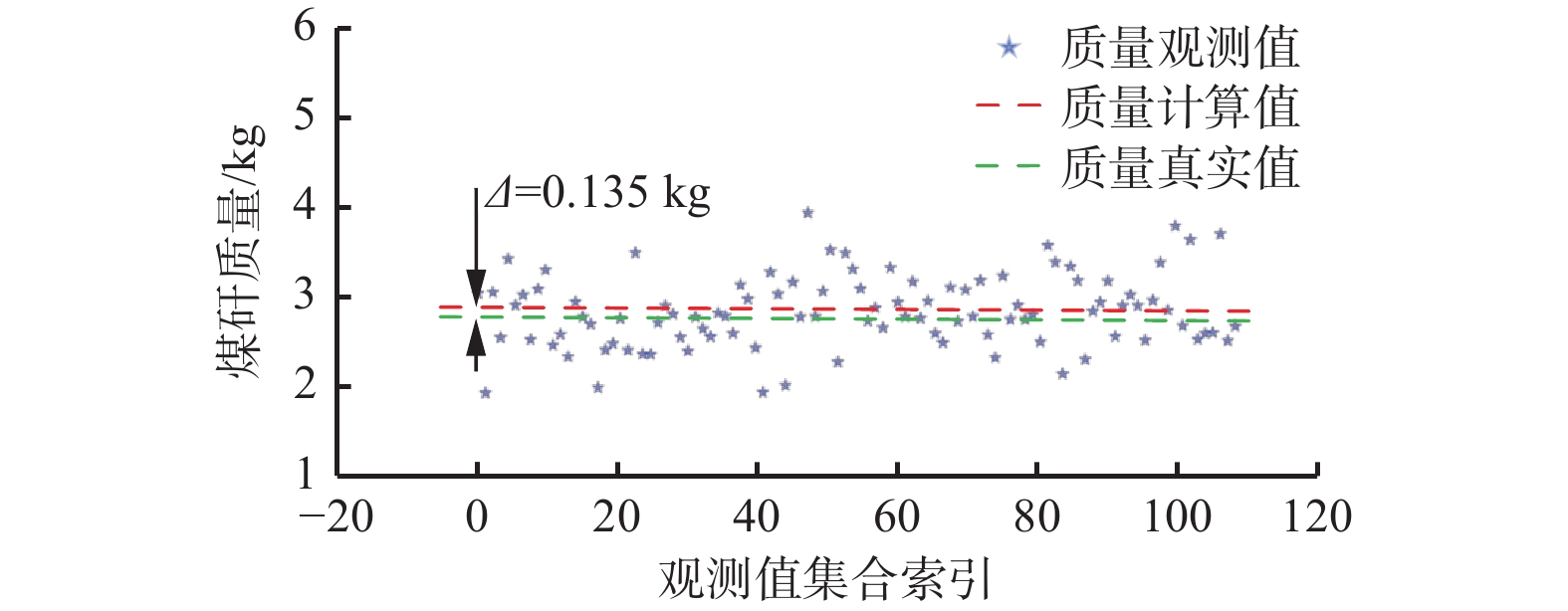
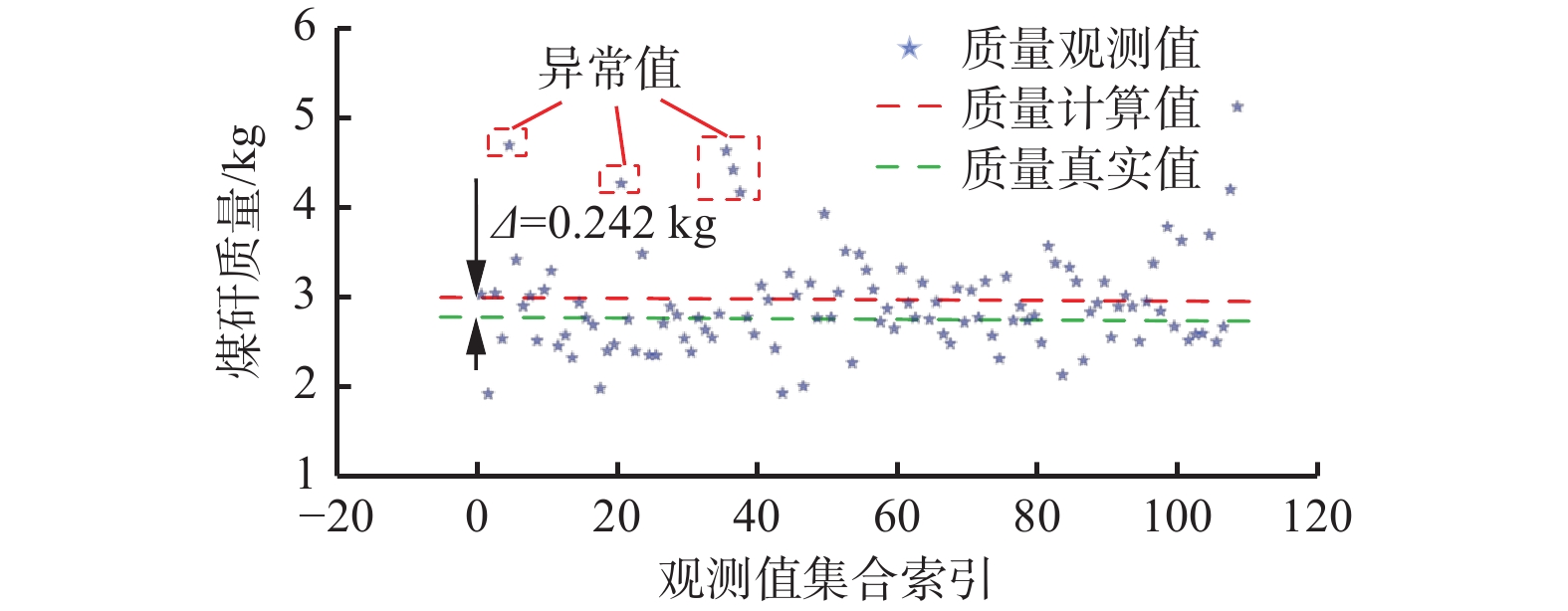
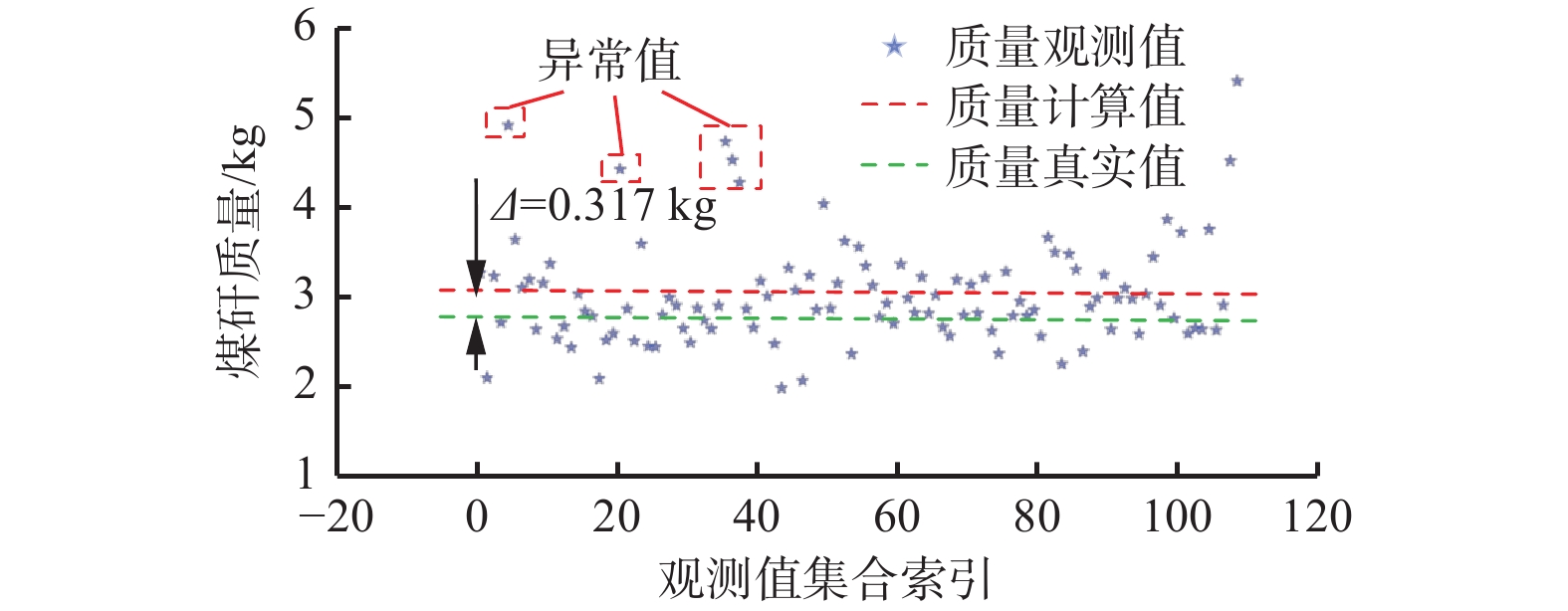
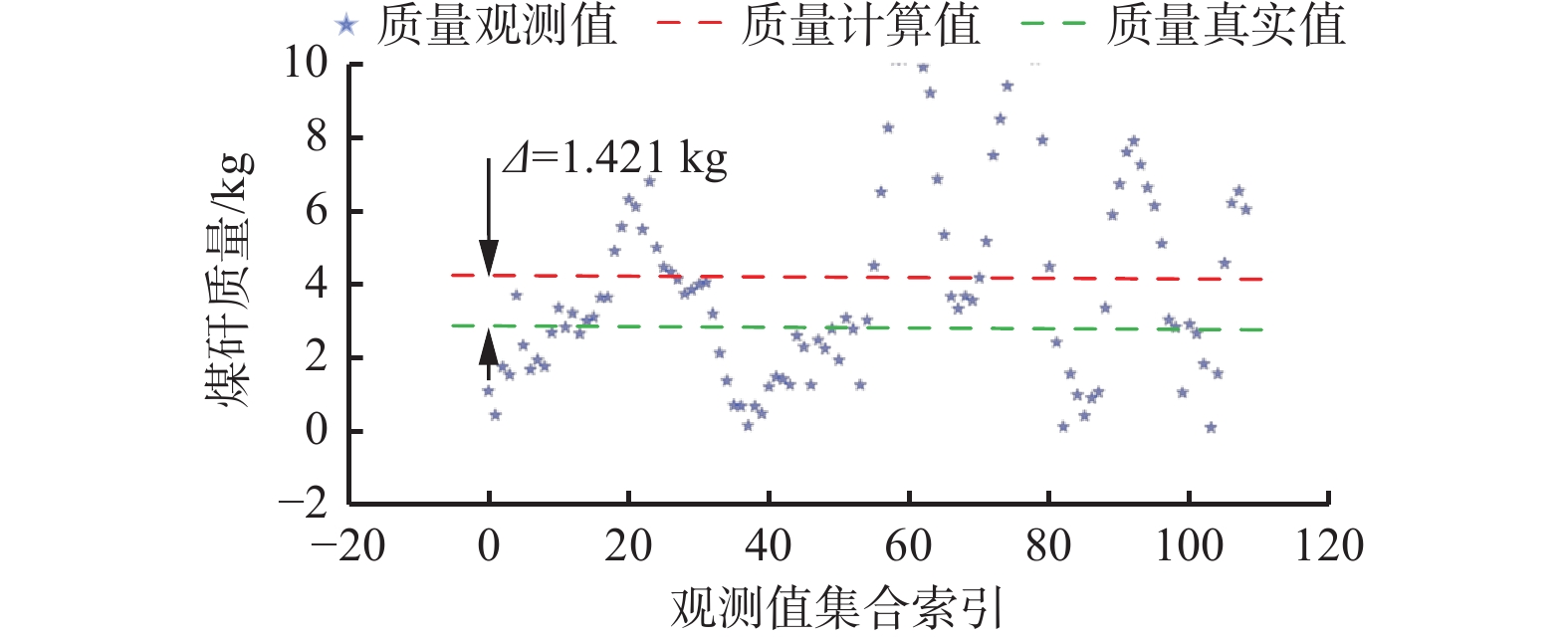
为进一步分析加速度补偿机制及异常值处理算法对称重模型的影响,将不同模型计算同一样本得出的煤矸质量观测值集合可视化,结果如图6—图9所示,Δ为动态称重模型计算值与真实值之间的差值。可看出完整模型M1因同时具备IQR算法和加速度补偿机制,观测值分布集中且误差最小;去除IQR算法的模型M2因异常值干扰导致误差增大;缺失x,y轴加速度补偿的模型M3因系统性偏差,导致误差进一步增大;同时缺失二者的模型M4观测值高度离散,无法实现煤矸质量的有效测量。
4.4.3 适用性分析
提出的动态称重方法旨在利用煤和矸石的密度差异实现煤矸二次识别,因此其称重误差需要满足煤最大检测密度小于矸石最小检测密度的条件,即
{\rho _{\mathrm{c}}}(1 + {\varepsilon _{\text{ρ}} }) \lt {\rho _{\mathrm{g}}}(1 - {\varepsilon _{\text{ρ}} }) (22) 式中:ρc,ρg分别为煤和矸石的真实密度;ερ为二次识别系统的密度检测误差。
由于密度等于质量除以体积,所以密度检测误差ερ可根据误差传递公式进一步由称重误差εm和体积检测误差εv表示:
{\varepsilon _{\text{ρ}}} = \sqrt {{\varepsilon _{\mathrm{m}}^2} + {\varepsilon _{\mathrm{v}}^2}} (23) 联立式(22)、式(23),可知煤矸动态称重方法的称重误差εm应满足:
{\varepsilon _{\mathrm{m}}} < \sqrt {{{\left(\frac{{{\rho _{\mathrm{g}}} - {\rho _{\mathrm{c}}}}}{{{\rho _{\mathrm{g}}} + {\rho _{\mathrm{c}}}}}\right)}^2} - {\varepsilon _{\mathrm{v}}^2}} (24) 本研究中ρc=1.45 g/cm3,ρg=1.80 g/cm3,煤和矸石的密度差为0.35 g/cm3。根据文献[12]中煤矸体积计算实验的相关结果,可知基于煤矸分拣机器人视觉识别模块可实现4.88%的煤矸体积计算误差,即εv=4.88%,代入相关参数可得εm<9.6%。由前文可知提出的动态称重方法平均称重误差为4.69%,远小于9.6%,因此本文方法能实现复杂工况下煤矸二次识别。
5. 结论
1) 提出一种融合多轴加速度补偿与异常值处理算法的在线动态称重方法。通过构建融合加速度的动态称重模型,结合IQR算法剔除质量观测值集合中的异常值,突破了传统静态称重在动态场景的适应性局限,解决了实际工况下的煤矸动态称重问题。
2) 实验结果表明,忽略三轴加速度补偿时称重误差达66.43%,引入z轴和x,y轴加速度补偿后误差分别降至12.97%,8.69%,加入IQR算法后误差进一步降至4.69%,可对密度差异大于0.35 g/cm3的煤和矸石实施二次识别,有效解决了实际复杂工况下煤矸识别准确率过低的问题。
-
表 1 z轴载荷与传感器输出值
Table 1 z-axis load and sensor output values
Fz/N 50 100 150 ··· 400 D 1 596 472 3 092 938 4 685 316 ··· 1 2361 424 表 2 x轴载荷与传感器输出值
Table 2 x-axis load and sensor output values
Fx/N 10 30 50 ··· 200 D 11 027 30 770 50 513 ··· 198 588 表 3 y轴载荷与传感器输出值
Table 3 y-axis load and sensor output values
Fy/N 10 30 50 ··· 200 D 9 968 28 355 45 786 ··· 181 967 表 4 动态称重实验结果
Table 4 Dynamic weighing experiment results
样本 真实质量/g 模型M1 模型M2 模型M3 模型M4 计算质量/g 误差/% 计算质量/g 误差/% 计算质量/g 误差/% 计算质量/g 误差/% 矸1 2 748 2 883 4.91 2 990 8.81 3 065 11.54 4 169 51.71 矸2 2 344 2 438 4.01 2 591 10.54 2 731 16.51 4 476 90.96 矸3 3 569 3 709 3.92 3 748 5.02 3 934 10.23 4 858 36.12 矸4 2 013 2 087 3.68 2 122 5.41 2 198 9.19 3 470 72.38 矸5 3 758 3 876 3.14 3 914 4.15 4 004 6.55 5 253 39.78 煤1 2 260 2 358 4.34 2 664 17.88 2 779 22.96 3 432 51.86 煤2 1 930 2 030 5.18 2 059 6.68 2 087 8.13 3 197 65.65 煤3 1 670 1 760 5.39 1 800 7.78 1 881 12.63 2 784 66.71 煤4 1 501 1 588 5.80 1 635 8.93 1 692 12.72 2 884 92.14 煤5 897 956 6.58 1 002 11.71 1 070 19.29 1 767 96.99 -
[1] 刘峰,郭林峰,赵路正. 双碳背景下煤炭安全区间与绿色低碳技术路径[J]. 煤炭学报,2022,47(1):1-15. LIU Feng,GUO Linfeng,ZHAO Luzheng. Research on coal safety range and green low-carbon technology path under the dual-carbon background[J]. Journal of China Coal Society,2022,47(1):1-15.
[2] 王国法,任怀伟,富佳兴. 煤矿智能化建设高质量发展难题与路径[J]. 煤炭科学技术,2025,53(1):1-18. DOI: 10.12438/cst.2024-0550 WANG Guofa,REN Huaiwei,FU Jiaxing. Challenge and path of high-quality development of coal mine intelligent construction[J]. Coal Science and Technology,2025,53(1):1-18. DOI: 10.12438/cst.2024-0550
[3] 李曼,段雍,曹现刚,等. 煤矸分选机器人图像识别方法和系统[J]. 煤炭学报,2020,45(10):3636-3644. LI Man,DUAN Yong,CAO Xiangang,et al. Image identification method and system for coal and gangue sorting robot[J]. Journal of China Coal Society,2020,45(10):3636-3644.
[4] 郭永存,何磊,刘普壮,等. 煤矸双能X射线图像多维度分析识别方法[J]. 煤炭学报,2021,46(1):300-309. GUO Yongcun,HE Lei,LIU Puzhuang,et al. Multi-dimensional analysis and recognition method of coal and gangue dual-energy X-ray images[J]. Journal of China Coal Society,2021,46(1):300-309.
[5] 张超,刘法政,刘善军,等. 基于热红外响应的煤矸智能识别方法试验研究[J/OL]. 金属矿山:1-9[2025-02-13]. http://kns.cnki.net/kcms/detail/34.1055.TD.20241024.1146.002.html. ZHANG Chao,LIU Fazheng,LIU Shanjun,et al. Experimental study on intelligent identification method of coal and gangue based on thermal infrared response[J/OL]. Metal Mine:1-9[2025-02-13]. http://kns.cnki.net/kcms/detail/34.1055.TD.20241024.1146.002.html.
[6] 李廉洁,樊书祥,王学文,等. 高光谱成像的煤与矸石分类[J]. 光谱学与光谱分析,2022,42(4):1250-1256. DOI: 10.3964/j.issn.1000-0593(2022)04-1250-07 LI Lianjie,FAN Shuxiang,WANG Xuewen,et al. Classification method of coal and gangue based on hyperspectral imaging technology[J]. Spectroscopy and Spectral Analysis,2022,42(4):1250-1256. DOI: 10.3964/j.issn.1000-0593(2022)04-1250-07
[7] 毛会淇,常安然,张雷,等. 激光反射率煤矸在线识别技术参数优化研究[J]. 煤炭技术,2021,40(11):224-226. MAO Huiqi,CHANG Anran,ZHANG Lei,et al. Optimization of laser reflectivity for coal and gangue identification[J]. Coal Technology,2021,40(11):224-226.
[8] 韦小龙,王方田,何东升,等. 基于CSPNet−YOLOv7目标检测算法的煤矸图像识别模型[J]. 煤炭科学技术,2024,52(增刊1):238-248. WEI Xiaolong,WANG Fangtian,HE Dongsheng,et al. Image recognition model of coal gangue based on CSPNet-YOLOv7 target detection algorithm[J]. Coal Science and Technology,2024,52(S1):238-248.
[9] 杨洋,李海雄,胡淼龙,等. 基于YOLOv5−SEDC模型的煤矸分割识别方法[J]. 工矿自动化,2024,50(8):120-126. YANG Yang,LI Haixiong,HU Miaolong,et al. Coal and gangue segmentation and recognition method based on YOLOv5-SEDC model[J]. Journal of Mine Automation,2024,50(8):120-126.
[10] SUN Zhiyuan,HUANG Linlin,JIA Ruiqing. Coal and gangue separating robot system based on computer vision[J]. Sensors,2021,21(4). DOI: 10.3390/S21041349.
[11] ZHANG Chen,ZHANG Chenglian. Coal gangue separation system based on density measurement[C]. IEEE International Conference on Computer Science and Automation Engineering,Zhangjiajie,2012:216-218.
[12] 袁娜. 基于多信息融合的煤矸二次识别方法研究[D]. 西安:西安科技大学,2022. YUAN Na. Research on secondary identification method of coal gangue based on multi-information fusion[D]. Xi'an:Xi'an University of Science and Technology,2022.
[13] ZHANG Zhen,LI Bing,ZHANG Yang,et al. Research on manipulator weighing based on flexible sensors[C]. The 6th International Symposium on Robotics & Intelligent Manufacturing Technology,Changzhou,2024:216-220.
[14] KOSIARA A,CHOŁODOWSKI J,SKURJAT A. Development of a prototype dynamic weighing system for single bucket excavator[M]//Dynamical Systems in Applications. Cham:Springer International Publishing,2018:217-228.
[15] 李达,郭晨霞,杨瑞峰. 基于改进PSO−BP算法的动态称重数据处理[J]. 电子测量技术,2021,44(20):132-136. LI Da,GUO Chenxia,YANG Ruifeng. Dynamic weighing data processing based on improved PSO-BP algorithm[J]. Electronic Measurement Technology,2021,44(20):132-136.
[16] 王秦越,钱振华,贺关丽,等. 基于扩展卡尔曼滤波的气力输送动态称重系统[J]. 计量学报,2022,43(5):624-628. DOI: 10.3969/j.issn.1000-1158.2022.05.10 WANG Qinyue,QIAN Zhenhua,HE Guanli,et al. Dynamic weighing system of pneumatic conveying based on extended Kalman filter algorithm[J]. Acta Metrologica Sinica,2022,43(5):624-628. DOI: 10.3969/j.issn.1000-1158.2022.05.10
[17] 章玉,杨其华,何雨辰,等. 皮带伸缩机动态称重数据处理优化算法研究[J]. 仪表技术与传感器,2023(8):114-119. DOI: 10.3969/j.issn.1002-1841.2023.08.019 ZHANG Yu,YANG Qihua,HE Yuchen,et al. Research on optimization algorithm of dynamic weighing data processing for belt telescopic conveyor[J]. Instrument Technique and Sensor,2023(8):114-119. DOI: 10.3969/j.issn.1002-1841.2023.08.019
[18] 曹现刚,李虎,王鹏,等. 基于跨模态注意力融合的煤炭异物检测方法[J]. 工矿自动化,2024,50(1):57-65. CAO Xiangang,LI Hu,WANG Peng,et al. A coal foreign object detection method based on cross modal attention fusion[J]. Journal of Mine Automation,2024,50(1):57-65.
[19] MCLAUGHLIN N B,CHEN Y. Effect of strain gage misalignment on cross sensitivity of extended ring (ER) transducers[J]. Canadian Biosystems Engineering,2012,54:2.23-2.31.
[20] 郭贵勇,钟剑锋,张秋坤,等. 多向运动寄生载荷分量对称重传感输出的影响[J/OL]. 吉林大学学报(工学版):1-11[2025-01-17]. https://doi.org/10.13229/j.cnki.jdxbgxb.20231023. GUO Guiyong,ZHONG Jianfeng,ZHANG Qiukun,et al. Effect of parasitic load components with multi-directional motion on weight-sensing outputs[J/OL]. Journal of Jilin University (Engineering and Technology Edition):1-11[2025-01-17]. https://doi.org/10.13229/j.cnki.jdxbgxb.20231023.
[21] 刘丹丹. 基于EMD的GNSS时间序列异常值探测算法[J]. 地球物理学进展,2021,36(5):1865-1873. DOI: 10.6038/pg2021FF0265 LIU Dandan. New method of outlier detection for GNSS coordinate time series based on EMD approach[J]. Progress in Geophysics,2021,36(5):1865-1873. DOI: 10.6038/pg2021FF0265
[22] 杨哲,李艳玲,张鹏,等. 基于M估计量及标准四分位间距的安全监测数据异常识别的改进方法[J]. 长江科学院院报,2020,37(6):77-80. DOI: 10.11988/ckyyb.20190335 YANG Zhe,LI Yanling,ZHANG Peng,et al. An improved method of anomaly recognition of dam safety monitoring data based on M-estimator and standard quartile range[J]. Journal of Yangtze River Scientific Research Institute,2020,37(6):77-80. DOI: 10.11988/ckyyb.20190335



 下载:
下载: