Analysis and constraint methods for intra-flow contention in multi-hop paths of wireless mesh networks in mines
-
摘要:
针对现有无线Mesh网络的多跳带宽无法支撑实时音视频类大通量业务的问题,分析了矿井Mesh无线多跳路径流内竞争机制,揭示了多跳带宽损失机理。指出大于6跳的多跳中继系统存在最优收敛比,具备约束多跳带宽1/n(n为链路数量)下降趋势的可能性,小于等于6跳的多跳中继系统不能约束1/n下降趋势。决定多跳中继系统存在最优收敛比的关键因素是载波侦听距离与稳定通信距离之比ΔS:当路径节点按ΔS=2均匀分布时,多跳带宽存在最优收敛比1/6;由于矿井无线传输的分界特性,ΔS≈3,导致矿井内路径节点均匀分布时的多跳带宽最优收敛比为1/8;矿井无线覆盖的不对称、不稳定特性造成节点不能均匀分布,因此模拟矿井 10 跳路径的多跳带宽最优收敛比为1/5。基于约束竞争范围的思想,提出异频分段串联混合组建链状网络的方法,在不修改Mesh协议的条件下,利用频率分割路径使流内竞争范围约束在各条路径内。实验结果表明,当无线链路数量大于10跳时,链状网络的首末带宽大于传统Mesh多跳路径的多跳带宽,同时收敛比也大于1/n,验证了该方法约束多跳带宽1/n下降趋势的可行性。
Abstract:To address the issue that the multi-hop bandwidth of existing wireless Mesh networks cannot support real-time, high-throughput services such as audio and video in mines, the intra-flow contention mechanism of multi-hop paths in mine wireless Mesh networks was analyzed, revealing the mechanism of multi-hop bandwidth degradation. It was pointed out that multi-hop relay systems with more than six hops have an optimal convergence ratio, which can potentially constrain the 1/n (n being the number of links) bandwidth degradation trend. However, systems with six or fewer hops cannot constrain this trend. The key factor determining the existence of an optimal convergence ratio is the ratio ΔS between the carrier sensing distance and the stable communication distance. When path nodes are uniformly distributed with ΔS=2, the optimal convergence ratio is 1/6. Due to the unique boundary characteristics of wireless transmission in mines, ΔS≈3, resulting in an optimal convergence ratio of 1/8 when nodes are uniformly distributed. However, the asymmetric and unstable nature of wireless coverage in mines prevents uniform node distribution. Therefore, for a 10-hop path in a simulated mine, the optimal convergence ratio is 1/5. Based on the idea of constraining the contention range, a method of constructing a chain network using frequency-division segmented serial hybrid links was proposed. Without modifying the Mesh protocol, this method constrained intra-flow contention within each path segment by splitting the path using different frequencies. Experimental results showed that when the number of wireless links exceeded ten hops, the bandwidth between the first and last nodes in the chain network was greater than the multi-hop bandwidth of traditional Mesh paths, and the convergence ratio also exceeded 1/n, validating the feasibility of the proposed method in constraining the 1/n bandwidth degradation trend.
-
0. 引言
矿井通风系统是煤矿安全的重要保障系统,担负着将新鲜空气送入井下、保证人员正常呼吸、稀释并排出有害气体、调节作业场所温湿度等作用[1]。要实现上述作用,必须保证矿井内各用风地点风量时刻满足需风量要求。然而,开采作业是动态变化过程,随着矿井周围环境变化,各巷道实际风量和需风量都是不断改变的,当巷道实际风量不满足需风量要求时,存在安全隐患。随着煤矿智能化发展,如何快速、智能地确定安全、高效、准确的风量调控方案,是矿井通风领域亟待解决的重大问题[2]。
近年来,元启发式算法由于其无需梯度信息、鲁棒性强等特点,被广泛应用于矿井风量调控优化问题。Wang Jinmiao等[3]以通风机功率最小为目标,建立了矿井通风系统网络优化的无约束数学模型,并利用黑燕鸥优化算法进行模型求解。吴新忠等[4]以目标用风分支风量可调最大化为目标,建立了风量调控数学模型,结合风网灵敏度的衰减特征[5-7],确定了模型中待优化风量的最优调节分支集及其风阻调节范围,缩小了可行域范围,提高了模型解算速度,同时提出了多策略融合麻雀搜索算法对模型进行求解。Li Junqiao等[8]通过引入权重系数,提出了基于通风机最小功耗和目标用风分支最大风量需求的目标函数,并应用改进粒子群优化(Particle Swarm Optimization,PSO)算法进行求解,在尽可能降低通风系统功率消耗的同时,增大了目标用风分支的风量。此外,灰狼优化算法[9]、鲸群优化算法[10]等元启发式算法也被应用于求解矿井风量调控优化模型。但采用元启发式算法求解无约束优化数学模型存在收敛速度较慢的问题。
本文提出了一种基于改进人工蜂群(Artificial Bee Colony,ABC)算法的矿井风量按需调控智能决策方法。构建以目标用风分支风量与理想风量差距最小为目标的矿井风量按需调控智能决策模型,利用拉格朗日松弛方法[11]、冲突数方法[12]、随机搜索方法[13]和元启发式算法[14]对模型进行优化,并采用改进ABC算法求解模型,可实现对矿井风量的快速、精准调控。
1. 矿井风量按需调控智能决策模型
1.1 矿井风量按需调控智能决策需求
为方便分析,将矿井巷道分为3类:目标用风分支、其他用风分支和一般分支。目标用风分支即需要通过风量调控决策使该分支风量达到预定值的巷道;其他用风分支即除目标用风分支外的采煤工作面、掘进工作面、独立通风硐室等用风地点需风量要求严格的巷道;一般分支即行人巷道、行车巷道和辅运巷等对风量不做要求的巷道。
矿井风量调控的目的是改变某一条或某几条目标用风分支的风量,使其满足安全生产需求。为达到该目的,在矿井的日常风量调控中,在总风量满足需求时,常通过调控风窗面积以改变巷道风阻,从而实现对目标用风分支的风量调节。因此,在保证其他用风分支和一般分支风量满足需风量要求的前提下,求解符合目标用风分支理想风量的矿井风阻调控方案,即矿井风量按需调控智能决策的实质。
1.2 矿井风量按需调控智能决策模型建立
假设第$ x $($ x $=1,2,$\cdots $,v,v为矿井风阻调控方案总数)个矿井风阻调控方案$ {R_x} = \{ {r_{x,1}},{r_{x,2}}, \cdots ,{r_{x,n}}\} $,其中$ {r_{x,j}} $为第$ x $个风阻调控方案中第$ j $($ j $=1,2,$\cdots $,n,n为通风网络分支总数)个分支风阻,此时第$ x $个矿井风阻调控方案中第$ j $个分支的风量$ {q_{x,j}} $与$ {R_x} $存在函数关系$ {f_j} $(·):
$$ {q_{x,j}} = {f_j}({R_x}) $$ (1) 矿井风量按需调控智能决策模型的目标函数可描述为
$$ F({R_x}) = \sum\limits_{t = 1}^{{z}} S_{ x,t} $$ (2) $$ S_{ x,t}=\left\{\begin{array}{l}\mathrm{min}(\left|f_t(R_x)-a_t\right|,\left|f_t(R_x)-b_t\right|) \quad f_t(R_x) < a_t \text{或}\\ \quad f_t(R_x) > b_t \\ 0\ \ \ \ a_t\leqslant f_t(R_x)\leqslant b_t\end{array}\right. $$ (3) 式中:$ {S_{ x,t}} $为第$ x $个矿井风阻调控方案中第t(t=1,2,$\cdots $,z,z为目标用风分支总数)个目标用风分支风量与其理想风量的差值;$f_t(R_x) $为第x个矿井风阻调控方案中第t个目标用风分支风量;$ {a_t} $,$ {b_t} $分别为第$ t $个目标用风分支风量的下限和上限。
矿井风量按需调控智能决策模型可建立为
$$ \left\{\begin{array}{l}\mathrm{min}F\text{(}R_x\text{)} \\ \mathrm{s.t.}\text{ }f_s(R_x)\leqslant b_s \qquad s=1,2,\cdots,n-z \\ \quad\;\; l_s(R_x)\leqslant c_s \\ \quad\;\;\displaystyle\sum_{j=1}^nd_{i,j}f_j(R_x)=0\text{ } \qquad i=1,2,\cdots,m-1 \\ \quad\;\;\displaystyle\sum_{j=1}^ne_{g,j}r_{x,j}\left|f_j(R_x)\right|f_j(R_x)-h_{{\mathrm{N}}j}=0 \qquad g=1,2,\cdots,\\ \qquad\quad n-m-1\\ \quad\;\; R_x\in G \end{array}\right. $$ (4) $$ {d}_{i,j}=\left\{\begin{array}{*{20}{l}}1& i节点为j分支端点且风量{q}_{x,j}流入该节点\\ -1& i节点为j分支端点且风量{q}_{x,j}流出该节点\\ 0& i节点不属于j分支的端点 \end{array} \right.$$ (5) $$ {e}_{g,j}=\left\{\begin{array}{*{20}{l}}1& j分支在g回路中且与g回路同向\\ -1& j分支在g回路中且与g回路反向\\ 0& j分支不属于g回路\end{array}\right.$$ (6) 式中:$ {f_s}({R_x}) $为第$ x $个矿井风阻调控方案中第$ s $个其他用风分支或一般分支风量;$ {b_s} $为第$ s $个其他用风分支或一般分支风量上限;$ {l_s}({R_x}) $为$ {f_s}({R_x}) $的负值;$ {c_s} $为第$ s $个其他用风分支或一般分支风量下限$ {a_s} $的负值;$ m $为通风网络节点数;$ h_{\mathrm{N}j} $为第j个分支自然风压;$ G $为矿井风阻调控方案集合,$ G=\left\{R_1,R_2,\cdots,R_v\right\} $。
1.3 矿井风量按需调控智能决策模型优化
1.3.1 基于拉格朗日松弛方法的模型优化
式(4)中第3个和第4个约束可由通风网络解算方法[15-16]进行求解,第5个约束是对决策变量$ {R_x} $取值的限制,且决策变量为连续变量。因此将第3个至第5个约束视为“简单”约束,第1个和第2个约束视为“难”约束。运用拉格朗日松弛方法,将难处理的约束通过拉格朗日乘子移到目标函数上,可将式(4)优化为
$$ \left\{\begin{array}{l}\mathrm{min}\text{ }F(R_x)+\displaystyle\sum_{s=1}^{n-{\textit{z}}}\lambda_s(f_s(R_x)-b_s)+\displaystyle\sum_{s=1}^{n-{\textit{z}}}\mu_s(l_s(R_x)-c_s) \\ \mathrm{s.t.}\text{ }\displaystyle\sum_{j=1}^nd_{i,j}f_j(R_x)=0 \\ \quad\;\;\displaystyle\sum_{j=1}^ne_{g,j}r_{x,j}\left|f_j(R_x)\right|f_j(R_x)-h_{{\mathrm{N}}j}=0\text{ } \\ \quad\;\;\lambda_s,\mu_s\geqslant0 \\ \quad\;\; R_x\in G\end{array}\right. $$ (7) 式中$ {\lambda _s} $,$ {\mu _s} $为第$ s $个其他用风分支或一般分支对应的拉格朗日乘子。
由式(7)可知,将式(4)中的第1个和第2个约束通过拉格朗日乘子移到目标函数上后,可行解将不需满足其他用风分支和一般分支风量符合各自需风量这一约束。此时,矿井风量按需调控智能决策模型的一个可行解为一组处于$ G $集合内,同时满足节点风量平衡定理和回路风压平衡定理的风阻集合。因此,该模型的可行域可利用通风网络解算中的Scott−Hinsley法进行刻画。
1.3.2 基于冲突数方法的模型优化
式(7)中的目标函数反映的是各分支风量与其风量上下限(需风量范围)之间的函数关系。为简化该式,引入冲突数的概念:在矿井风量按需调控智能决策模型中,冲突数可理解为矿井风阻调控方案下,风量不处于其需风量范围的分支数。若某分支的风量不处于其需风量范围,则认为该分支的风量与实际需风量发生了冲突,此时该分支的冲突数$ {T_{x,j}} $为1,反之为0。总冲突数$ P({R_x}) $表示在第$ x $个矿井风阻调控方案下矿井所有分支发生冲突情况的总数,当$ P({R_x}) $为0时,代表在第$ x $个矿井风阻调控方案下,通风网络中每条分支风量均处于其需风量范围中,此时对应的矿井风阻调控方案即为最优的矿井风量按需调控决策。
运用冲突数方法可将式(7)中的目标函数改进为
$$ P({R_x}) = \sum\limits_{j = 1}^n {{T_{x,j}}} $$ (8) $$ T_{x,j}=\left\{\begin{gathered}1\text{ }\ \ f_j(R_x)\notin[a_j,b_j] \\ 0\text{ }\ \ f_j(R_x)\in[a_j,b_j] \\ \end{gathered}\right. $$ (9) 则式(7)可优化为
$$ \left\{\begin{gathered}\min\text{ }P(R_x) \\ \mathrm{s.t.\text{ }}\sum\limits_{j=1}^nd_{i,j}f_j(R_x)=0 \\ \quad\;\;\sum\limits_{j=1}^ne_{g,j}r_{x,j}\left|f_j(R_x)\right|f_j(R_x)-h_{{\mathrm{N}}j}=0 \\ \quad\;\; R_x\in G \\ \end{gathered}\right. $$ (10) 1.3.3 基于随机搜索方法的模型优化
由于式(1)的函数关系是假设的,目前并没有一个方程能够准确描述$ {q_{x,j}} $与$ {R_x} $之间的关系,所以难以讨论式(10)中目标函数和约束条件的凹凸性、导数信息、KKT条件的约束规范、有效集等性质,导致无法利用矿井风阻调控方案$ {R_x} $对应的矿井风量$ {Q_x} $=$ \left\{ {{q_{x,1}},{q_{x,2}}, \cdots ,{q_{x,n}}} \right\} $的变化趋势精确求解矿井风阻调控方案$ {R_x} $的搜索方向和搜索步长,不能通过最速下降法和共轭梯度法求解矿井风量按需调控智能决策模型。因此,采用无需利用$ q{}_{x,j} $与$ {R_x} $之间的函数关系,也可获得矿井风阻调控方案$ {R_x} $的搜索方向和搜索步长的随机搜索方法,将式(10)优化为
$$ \left\{\begin{gathered}\min\text{ }P(Q_x) \\ \mathrm{s.t.}\text{ }\sum\limits_{j=1}^nd_{i,j}q_{x,j}=0 \\ \quad\;\;\sum\limits_{j=1}^ne_{g,j}r_{x,j}\left|q_{x,j}\right|q_{x,j}-h_{{\mathrm{N}}j}=0 \\ \quad\;\; R_x\in G \\ \end{gathered}\right. $$ (11) 1.3.4 基于元启发式算法的模型优化
由式(8)和式(9)可知,当任何分支风量不处于该分支的需风量范围时,都会使目标函数值增加1,即式(8)并不能体现出目标用风分支、其他用风分支和一般分支这3类巷道的区别。由式(8)计算出的目标函数值并不会引导寻优方案优先向使目标用风分支满足其需风量范围的可行解移动。为使目标函数值在目标用风分支维度下降得更迅速,对不同类型的分支依据其需风量范围,引入权重系数$ {p_j} $,最终将式(11)优化为
$$ \left\{\begin{gathered}\min\text{ }P(Q_x) \\ \mathrm{s.t.}\text{ }\sum\limits_{j=1}^nd_{i,j}q_{x,j}=0 \\ \qquad\sum\limits_{j=1}^ne_{g,j}r_{x,j}\left|q_{x,j}\right|q_{x,j}-h_{\mathrm{N}j}=0 \\ \qquad R_x\in G \\ \end{gathered}\right. $$ (12) $$ P({Q_x}) = \sum\limits_{j = 1}^n {{p_j}{T_{x,j}}} $$ (13) 2. 矿井风量按需调控智能决策
2.1 基于ABC算法的矿井风量按需调控智能决策
ABC算法是通过模拟自然界蜜蜂分工采蜜行为而得到的一种元启发式算法,具有结构简单、控制参数少、鲁棒性强等优点[17],在应对高维度非线性优化问题上表现出优秀的求解能力[18]。
将矿井风量按需调控智能决策模型中的矿井风阻调控方案$ {R_x} $视为蜜源位置,目标函数$ P({Q_x}) $视为蜜源质量(由式(12)可知$ P({Q_x}) $越小,蜜源质量越优),则基于ABC算法的矿井风量按需调控智能决策的寻优过程如下:
1) 种群初始化。通过初始化方程生成矿井风阻调控方案集合$ G $。
$$ r_{x,j}=r_{j\min}+\mathrm{rand}(0,1)(r_{j\max}-r_{j\min}) $$ (14) 式中:rand(0,1)为[0,1]上的随机数;$ r_{j\mathrm{m}\text{ax}},r_{j\min} $分别为第$ j $个分支风阻的上下限。
2) 采蜜行为。采蜜蜂在可行域内局部搜索新的矿井风阻调控方案,具体搜索方程可表示为
$$ {r'_{x,j}} = {r_{x,j}} + \phi ({r_{x,j}} - {r_{k,j}}) $$ (15) 式中:$ {r'_{x,j}} $为经搜索后的第$ x $个新的矿井风阻调控方案$ {R'_x} $中第$ j $个分支的风阻,$ {R'_x} = \{ {r'_{x,1}},{r'_{x,2}}, \cdots ,{r'_{x,n}}\} $;$ \phi $为[−1,1]上均匀分布的随机数;$ {r_{k,j}} $为随机选出的第$ k $$ (k \ne x) $个矿井风阻调控方案中第$ j $个分支的风阻。
若$ {R'_x} $的目标函数值优于$ {R_x} $,$ {R'_x} $将取代原矿井风阻调控方案$ {R_x} $,否则继续以$ {R_x} $作为矿井风阻调控方案。
3) 跟随行为。当采蜜蜂完成搜索后,会将新的蜜源信息分享给跟随蜂,每一只跟随蜂都会根据每个矿井风阻调控方案的目标函数值,以一定的概率选择适应度值较大的优质矿井风阻调控方案,在其周围采用搜索方程(式(15))进行局部搜索。每个矿井风阻调控方案的适应度函数$ H({R_x}) $及跟随蜂选择对应优质矿井风阻调控方案的概率$ {w_x} $分别为
$$ H({R_x}) = \frac{1}{{1 + P({Q_x})}}{\text{ }} $$ (16) $$ {w_x} = \frac{{H({R_x})}}{\displaystyle \sum_{x = 1}^v {H({R_x})} }{\text{ }} $$ (17) 4) 侦察行为。若某一矿井风阻调控方案在经历$ L $只蜜蜂搜索后仍未找到比它适应度值更大的优质矿井风阻调控方案,此时认为该矿井风阻调控方案为局部最优解。为跳出局部最优解,采蜜蜂会转变为侦察蜂,利用式(14)在整个可行域搜索新的矿井风阻调控方案,直到找到目标函数值更优的矿井风阻调控方案。
2.2 基于改进ABC算法的矿井风量按需调控智能决策
由于ABC算法中引入了较多的随机因子,导致该算法的探索能力较强而利用能力不足,在求解矿井风量按需调控智能决策模型时存在收敛速度较慢的问题。为平衡ABC算法的探索能力和利用能力,结合PSO算法[19]和一般反向学习(Generalized Opposition-based Learning,GOBL)策略[20]对ABC算法进行改进。
2.2.1 采蜜行为改进
PSO算法的灵感来源于鸟群或鱼群通过群体协助进行觅食的行为,在PSO算法中粒子根据个体历史最优值和群体历史最优值调整搜索方向,PSO算法拥有很强的利用能力,因此在蜜蜂的采蜜行为中引入群体历史最优值对搜索方向进行引导,将采蜜行为的搜索方程改进为
$$ {r'_{x,j}} = {r_{x,j}} + \phi ({r_{x,j}} - {r_{k,j}}) + \varphi ({r_{{\mathrm{best}},j}} - {r_{x,j}}){\text{ }} $$ (18) 式中:$ \varphi $为[0,1.5]上均匀分布的随机数;$ r_{\mathrm{best},j} $为当前最优的矿井风阻调控方案$ R_{\mathrm{best}} $在第$ j $个分支的风阻。
2.2.2 侦察行为改进
GOBL策略的核心机制:针对当前种群中的候选解,同步生成其一般反向解,通过贪婪准则选择适应度值更优的解作为下一代种群个体。该策略可提升算法的探索能力,从而提高算法收敛到全局最优解的概率。为保留原局部最优解的有用信息,将侦察行为的搜索方程改进为
$$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{x,j}} = {\mathrm{rand}}(0,1)({r_{j\min }}+{r_{j\max }}) - {r_{x,j}} $$ (19) 式中$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{x,j}} $为第$ x $个矿井风阻调控方案的反向解$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} _x} $中第$ j $个分支的风阻。
若一般反向解$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{x,j}} $未在边界调节范围$ [{r_{j\min }},{r_{j\max }}] $内,则采用随机生成的方法进行重置:
$$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{r} _{x,j}} = {\mathrm{rand}}({r_{j\min }},{r_{j\max }}) $$ (20) 式中$ \mathrm{rand}(r_{j\min},r_{j\max}) $为区间$ [{r_{j\min }},{r_{j\max }}] $上的随机数。
将一般反向解和利用式(14)产生的随机解进行比较,择优选择新蜜源的位置,该过程可表示为
$$ {R_x} = \left\{ \begin{gathered} {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_x}\quad P({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_x}) < P({R_x}) \\ {R_x}\quad {\text{其他}} \\ \end{gathered} \right. $$ (21) 3. 实验与分析
3.1 实验参数
实验目标:求解使目标用风分支风量调节至32 m3/s的风量调控决策。实验所用通风网络拓扑如图1所示,该通风网络初始数据见表1,各分支类型、风阻和风量调节范围见表2。为验证改进ABC算法性能,与ABC算法、PSO算法、基于全局最优的人工蜂群(Gbest-guided Artificial Bee Colony,GABC)算法[21]和基于一般反向学习的人工蜂群(Artificial Bee Colony with Generalized Opposition-Based Learning,ABC−GOBL)算法[22]进行对比。各算法主要参数设置:种群规模为100,最大抛弃次数为60,最大迭代次数为200。
表 1 通风网络初始数据Table 1. Ventilation network initial data分支
编号风阻/
(N·s2·m−8)风量/
(m3·s−1)分支
编号风阻/
(N·s2·m−8)风量/
(m3·s−1)1 0.006455 129.50 9 0.114862 12.32 2 0.004709 29.96 10 0.085501 14.27 3 0.009727 20.85 11 0.001561 62.09 4 0.001339 73.38 12 0.001391 73.38 5 1.572439 5.31 13 0.015521 50.81 6 0.001562 62.10 14 0.005727 129.50 7 0.232000 11.28 15 0 129.50 8 0.013821 35.51 表 2 通风网络各分支类型、风阻和风量调节范围Table 2. Branch types, air resistance, and airflow regulation range of the ventilation network分支编号 分支类型 风阻调节范围/(N·s2·m−8) 风量调节范围/(m3·s−1) 1 一般分支 0.006455 129.50 2 其他用风分支 0.004709 26.96~32.96 3 其他用风分支 0.009727 18.77~22.94 4 一般分支 0.001339 3.94~126.00 5 一般分支 1.572439 3.94~126.00 6 一般分支 0.001562 3.94~126.00 7 其他用风分支 0.040940 ~0.884324 10.15~12.41 8 一般分支 0.013821 ~0.844314 3.94~126.00 9 其他用风分支 0.016615 ~0.577616 11.09~13.55 10 目标用风分支 0.085501 31.50~32.50 11 一般分支 0.001561 3.94~126.00 12 一般分支 0.001391 3.94~126.00 13 一般分支 0.004964 ~0.714323 3.94~126.00 14 其他用风分支 0.005727 129.50 15 虚拟分支 0 129.50 3.2 实验结果分析
实验中每个算法独立运行30次,不同算法的迭代收敛曲线如图2所示,不同算法下模型求解结果见表3。
表 3 不同算法下模型求解结果Table 3. Model solution results under different algorithms算法 算法成功率/% 平均收敛代数 平均寻优时间/s 改进ABC 100 42 132.72 GABC 87 53 167.48 ABC−GOBL 100 122 385.52 ABC 100 158 516.68 PSO 0 - - 由图2和表3可知:改进ABC算法能在132.72 s稳定将目标函数值收敛到0,这是由于改进ABC算法在引入全局最优解对搜索方向进行引导的同时,加入一般反向解保留搜索经验,能使算法在保持较高探索能力的同时,提高算法的利用能力;GABC算法虽然能在167.48 s实现寻优,但在解算时会出现早熟现象,这是由于GABC算法虽然采用全局最优解提高了算法的利用能力,但在求解矿井风量按需调控模型时仍存在不能跳出局部最优解的情况;ABC−GOBL算法和ABC算法均能稳定收敛但速度较慢,平均收敛时间分别为385.52 s和516.68 s,而ABC−GOBL算法收敛速度快于ABC算法,这是由于该算法在侦查蜂阶段保留了种群记忆;PSO算法无法正常求解矿井风量按需调控智能决策模型,这是由于PSO算法同时利用个体最优解和全局最优解引导搜索,过度提升了算法的利用能力,导致该算法容易陷入局部最优解。
由改进ABC算法求解出的最优矿井风阻调控方案见表4。可看出当分支风阻r7,r8,r9,r13分别为0.871 307,0.209 715,0.571 217,0.051 381 N·s2/m8时,目标用风分支(第10个分支)的风量由14.27 m3/s增加至31.51 m3/s,该风量满足目标用风分支的需风量(31.50~32.50 m3/s)要求,与目标用风分支的期望风量32 m3/s仅有0.49 m3/s的误差,且调控后各分支风量均能满足需风量要求。
表 4 改进ABC算法求解出的最优矿井风阻调控方案Table 4. Optimal mine ventilation resistance control scheme solved by the improved artificial bee colony algorithm分支
编号风阻/
(N·s2·m−8)风量/
(m3·s−1)分支
编号风阻/
(N·s2·m−8)风量/
(m3·s−1)1 0.006455 129.50 9 0.571217 12.21 2 0.004709 27.25 10 0.085501 31.51 3 0.009727 18.96 11 0.001561 64.23 4 0.001339 74.83 12 0.001391 74.83 5 1.572439 8.49 13 0.051381 46.21 6 0.001562 64.23 14 0.005727 129.50 7 0.871307 10.60 15 0 129.50 8 0.209715 20.51 4. 结论
1) 以目标用风分支风量与理想风量差距最小为目标,建立了矿井风量按需调控智能决策模型,并运用拉格朗日松弛方法优化模型的约束条件,采用冲突数方法优化模型的目标函数,利用随机搜索方法和元启发式算法优化模型的搜索策略。
2) 针对ABC算法探索能力和利用能力不平衡的问题,在采蜜蜂局部寻优时引入群体历史最优解引导采蜜行为,并利用GOBL策略保存侦查蜂的搜索经验,提出了一种改进ABC算法。
3) 将改进ABC算法用于求解矿井风量调控决策模型,相较于PSO,ABC,GABC,ABC−GOBL等算法具有更高的收敛速度和稳定性,且寻优精度高。
-
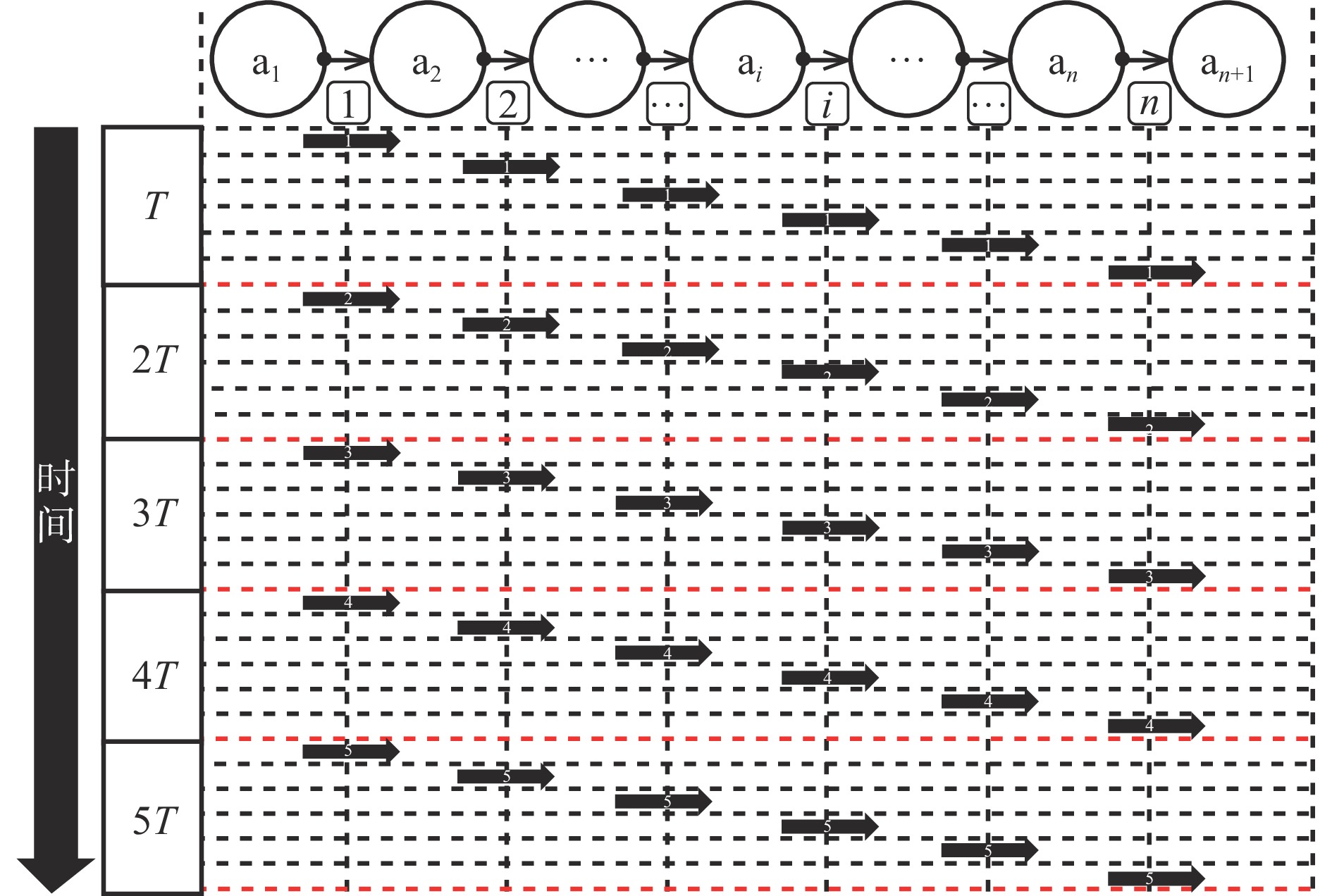
表 1 10跳路径各链路竞争秩
Table 1 Competition rank of each link in the 10-hop path
链路 施加影响
的链路可施加
的冲突权重 秩 链路 施加影响
的链路可施加
的冲突权重 秩 1 2 ①,② 1.1 3.7 6 4 ① 1.0 5.7 3 ①,② 1.1 5 ① 1.0 4 ③ 1.5 7 ①,② 1.1 2 1 ① 1.0 4.7 8 ①,② 1.1 3 ①,② 1.1 9 ③ 1.5 4 ①,② 1.1 7 5 ① 1.0 5.7 5 ③ 1.5 6 ① 1.0 3 1 ① 1.0 5.7 8 ①,② 1.1 2 ① 1.0 9 ①,② 1.1 4 ①,② 1.1 10 ③ 1.5 5 ①,② 1.1 8 6 ① 1.0 4.2 6 ③ 1.5 7 ① 1.0 4 2 ① 1.0 5.7 9 ①,② 1.1 3 ① 1.0 10 ①,② 1.1 5 ①,② 1.1 9 7 ① 1.0 3.1 6 ①,② 1.1 8 ① 1.0 7 ③ 1.5 10 ①,② 1.1 5 3 ① 1.0 5.7 10 8 ① 1.0 2.0 4 ① 1.0 9 ① 1.0 6 ①,② 1.1 7 ①,② 1.1 8 ③ 1.5 注:①表示相邻链路相互干扰退避过程;②表示链路之间的同步碰撞;③表示隐藏节点导致的链路对链路的异步碰撞。 表 2 1~10跳路径各链路竞争秩和最优收敛比
Table 2 Competition rank and optimal convergence ratio of each link in the 1-hop to 10-hop path
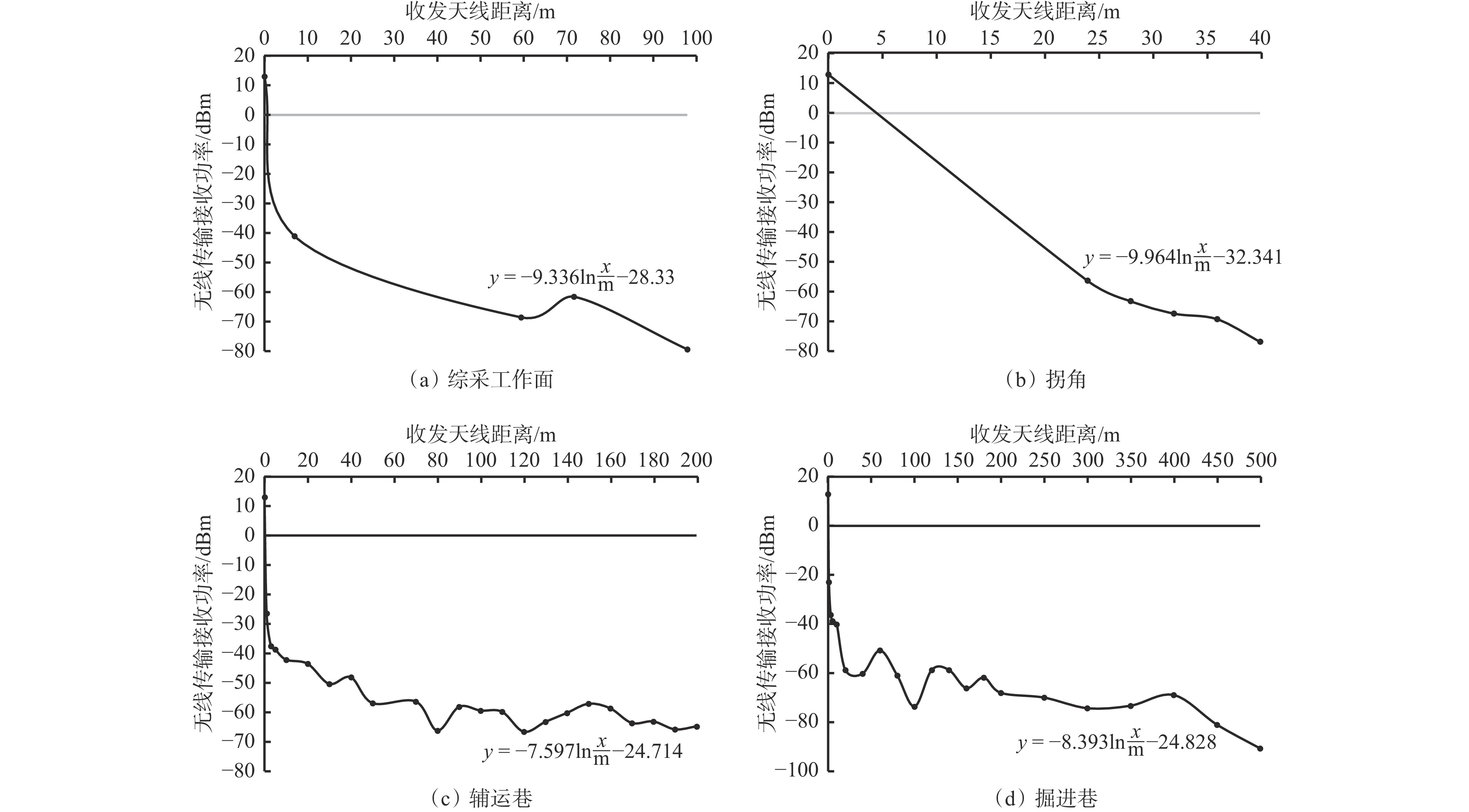
链路 秩 3跳 4跳 5跳 6跳 7跳 8跳 9跳 10跳 1 2.2 3.7 3.7 3.7 3.7 3.7 3.7 3.7 2 2.1 3.2 4.7 4.7 4.7 4.7 4.7 4.7 3 2.0 3.1 4.2 5.7 5.7 5.7 5.7 5.7 4 — 2.0 3.1 4.2 5.7 5.7 5.7 5.7 5 — — 2.0 3.1 4.2 5.7 5.7 5.7 6 — — — 2.0 3.1 4.2 5.7 5.7 7 — — — — 2.0 3.1 4.2 5.7 8 — — — — — 2.0 3.1 4.2 9 — — — — — — 2.0 3.1 10 — — — — — — — 2.0 最优收敛比 1/3 1/4 1/5 1/6 1/6 1/6 1/6 1/6 表 3 矿井无线覆盖范围比值
Table 3 Ratio of wireless coverage range in mines
巷道类型 载波频率/GHz 无线传输损耗拟合公式 信号 覆盖距离/m ΔS ΔI 用途 强度/dBm 综采工作面 5.4 y = −9.336ln$\dfrac{x}{{\rm{m}}} $−28.33 载波侦听下界 −80 254.49 2.93 1.37 干扰下界 −73 119.56 稳定通信下界 −70 86.74 拐角 5.4 y = −9.964ln $\dfrac{x}{{\rm{m}}} $−32.341 载波侦听下界 −80 119.81 2.75 1.35 干扰下界 −73 59.04 稳定通信下界 −70 43.43 辅运巷 5.4 y = −7.597ln$\dfrac{x}{{\rm{m}}} $−24.714 载波侦听下界 −80 1 462.22 3.77 1.47 干扰下界 −73 571.65 稳定通信下界 −70 387.55 掘进巷 5.4 y = −8.393ln$\dfrac{x}{{\rm{m}}} $−24.828 载波侦听下界 −80 716.49 3.28 1.41 干扰下界 −73 309.46 稳定通信下界 −70 218.23 表 4 矿井多跳路径链路竞争秩
Table 4 Link competition rank of multi-hop path in mines
直巷覆盖 不对称覆盖 不稳定覆盖 链路号 秩 链路号 秩 链路号 秩 1 4.7 1 4.1 1 4.1 2 5.7 2 3.2 2 3.2 3 6.7 3 5.1 3 5.1 4 7.7 4 4.2 4 4.2 5 7.7 5 6.6 5 3.6 6 7.7 6 5.7 6 4.6 7 6.2 7 3.2 7 2.1 8 5.2 8 4.2 8 3.6 9 4.2 9 4.2 9 2.0 10 3.0 10 1.0 10 1.0 表 5 实验部署参数
Table 5 Experimental deployment parameters
实验名称 第1条路径 第2条路径 第3条路径 频率/
GHz跳数 链路带宽/
(Mbit·s−1)多跳带宽/
(Mbit·s−1)频率/
GHz跳数 链路带宽/
(Mbit·s−1)多跳带宽/
(Mbit·s−1)频率/
GHz跳数 链路带宽/
(Mbit·s−1)多跳带宽/
(Mbit·s−1)楼道实验Ⅰ 1.4 2 20 10.00 2.4 2 20 10.00 — — — — 楼道实验Ⅱ 1.4 1 20 20.00 2.4 3 20 6.66 — — — — 楼道实验Ⅲ 2.4 4 20 5.00 5.8 4 80 20.00 — — — — 巷道实验Ⅰ 2.4 4 20 5.00 5.8 4 80 20.00 1.4 1 20 20 巷道实验Ⅱ 1.4 3 20 6.66 2.4 7 20 2.85 5.8 10 80 8 1.4 3 20 6.66 2.4 7 20 2.85 5.8 5 80 16 文献实验Ⅰ 2.4 10 54 5.40 — — — — — — — — 2.4 15 54 3.60 — — — — — — — — 文献实验Ⅱ 2.4 15 56 3.73 — — — — — — — — 表 6 实测链状网络首末传输速率及抖动范围
Table 6 Measured end-to-end transmission rate and jitter range of the chain network
实验名称 端到端方向 总跳数 理论带宽Ⅰ/
(Mbit·s−1)理论带宽Ⅱ/
(Mbit·s−1)实测首末速率/
(Mbit·s−1)首末速率抖动/
(Mbit·s−1)首末速率
对应收敛比楼道实验Ⅰ A3→C1 4 5.00 10.00 5.1 4.70~5.90 1/3.9 楼道实验Ⅱ A4→C1 4 5.00 6.60 4.2 2.70~5.90 1/4.6 楼道实验Ⅲ B5→A1 8 2.50~10.00 5.00 4.9 2.70~7.30 1/7.4~1/10.8 巷道实验Ⅰ C2→A1 9 2.20~8.80 5.00 5.1 4.20~6.00 1/4.7~1/13.3 巷道实验Ⅱ B1→C1 15 1.30~5.30 2.85 4.5 3.15~6.90 1/6.3~1/11.5 B6→C1 20 1.00~4.00 2.85 4.4 3.80~5.70 1/5.2~1/14.0 文献实验Ⅰ — 10 5.40 — 1.4 — 1/38.5 — 15 3.60 — 0.6 — 1/90.0 文献实验Ⅱ — 15 3.73 — 2.0 — 1/28.0 -
[1] 王虎. 矿井救援无线Mesh通信信号衰减特性研究[D]. 西安:西安科技大学,2019. WANG Hu. Research on signal attenuation characteristics of mine communication wireless Mesh[D]. Xi'an:Xi'an University of Science and Technology,2019.
[2] 孙继平. 矿井无线传输的特点[J]. 煤矿设计,1999,31(4):20-22. SUN Jiping. Characteristics of wireless transmission in mine[J]. Coal Engineering,1999,31(4):20-22.
[3] 孙继平,徐卿. 矿井无线中继应急通信系统实现方法[J]. 工矿自动化,2021,47(5):1-8. SUN Jiping,XU Qing. Implementation method of mine wireless relay emergency communication system[J]. Industry and Mine Automation,2021,47(5):1-8.
[4] 郭星歌. 矿井无线网格网技术的研究及应用[D]. 徐州:中国矿业大学,2013. GUO Xingge. Research and application of wireless mesh network technology in coal mine[D]. Xuzhou:China University of Mining and Technology,2013.
[5] 宋文,戴剑波,王飞,等. 矿井WMN多媒体应急通信系统多跳传输性能研究[J]. 煤炭学报,2011,36(4):706-710. SONG Wen,DAI Jianbo,WANG Fei,et al. Research on the multi-hop performance of underground mine emergency communication system based on WMN[J]. Journal of China Coal Society,2011,36(4):706-710.
[6] 王晖. 一种单信道无线传感器网络的隐藏终端和暴露终端问题解决方案[J]. 电子技术应用,2008,34(9):87-90,95. DOI: 10.3969/j.issn.0258-7998.2008.09.032 WANG Hui. A solution of hidden-terminal and exposed-terminal problem for single channel WSN network[J]. Application of Electronic Technique,2008,34(9):87-90,95. DOI: 10.3969/j.issn.0258-7998.2008.09.032
[7] 虞万荣. 无线自组网MAC协议关键技术研究[D]. 长沙:国防科学技术大学,2006. YU Wanrong. Research of MAC protocols in wireless Ad Hoc networks[D]. Changsha:National University of Defense Technology,2006.
[8] 张棋飞. 无线自组织网络媒体接入控制机制研究[D]. 武汉: 华中科技大学, 2007. ZHANG Qifei.Research on medium access control in wireless Ad Hoc networks[D]. Wuhan: Huazhong University of Science and Technology, 2007.
[9] 赵海涛. 多跳无线网络中可用带宽的估计和预测[D]. 长沙:国防科学技术大学,2009. ZHAO Haitao. Available bandwidth estimation and prediction in multi-hop wireless networks[D]. Changsha:National University of Defense Technology,2009.
[10] 刘少阳, 赵海涛, 魏急波, 等. 多跳无线网络中路径端到端容量的准确计算[J]. 软件学报,2013,24(1):164-174. LIU Shaoyang, ZHAO Haitao, WEI Jibo, et al. Accurate calculation of end-to-end throughput capacity for wireless multi-hop networks[J]. Journal of Software,2013,24(1):164-174.
[11] SANZGIRI K,CHAKERES I D,BELDING-ROYER E M. Determining intra-flow contention along multihop paths in wireless networks[C]. First International Conference on Broadband Networks,San Jose,2004:611-620.
[12] 宋安. 无线自组织网络性能分析模型与可用带宽估计研究[D]. 长沙:国防科学技术大学,2011. SONG An. Performance modeling and available bandwidth estimation in wireless Ad Hoc networks[D]. Changsha:National University of Defense Technology,2011.
[13] 尹金钺. 井下无线电传播[J]. 煤炭科学技术,1974,2(1):72-81. YIN Jinyue. Underground radio propagation[J]. Coal Science and Technology,1974,2(1):72-81.
[14] 肖公亮. 对无线电波在矿井中传播的几点看法[J]. 煤矿自动化,1980,6(1):61-62. XIAO Gongliang. Some views on the propagation of radio waves in mines[J]. Coal Mine Automation,1980,6(1):61-62.
[15] 王胜坤,张立毅,张守兵. 矿井隧道中无线电波的自由传播[J]. 煤炭科学技术,1989,17(3):52-54,61. WANG Shengkun,ZHANG Liyi,ZHANG Shoubing. Free propagation of radio waves in mine tunnels[J]. Coal Science and Technology,1989,17(3):52-54,61.
[16] 陈廷龙. 降低电波在隧道中传播损耗的措施[J]. 电波与天线,1995,20(2):43-46. CHEN Tinglong. Measures to reduce the propagation loss of radio waves in tunnels[J]. Radio Waves and Antennas,1995,20(2):43-46.
[17] 孙继平,魏占永. 矿井隧道中电磁场能量的损耗[J]. 中国矿业大学学报,2002,31(6):575-578. DOI: 10.3321/j.issn:1000-1964.2002.06.007 SUN Jiping,WEI Zhanyong. Loss of electromagnetic energy in mine tunnel[J]. Journal of China University of Mining & Technology,2002,31(6):575-578. DOI: 10.3321/j.issn:1000-1964.2002.06.007
[18] 姚善化. 复杂矿井巷道中电磁波传播特性及相关技术研究[D]. 合肥:安徽大学,2010. YAO Shanhua. Study on characteristic of electromagnetic waves propagation and key technology in complicated coal mine tunnels[D]. Hefei:Anhui University,2010.
[19] 王逸飞,王怡雯,许议丹,等. 基于射线追踪路径损耗模型的煤矿巷道基站选址方法[J]. 工矿自动化,2024,50(11):70-77. WANG Yifei,WANG Yiwen,XU Yidan,et al. Coal mine roadway base station site selection method based on ray-tracing path loss model[J]. Journal of Mine Automation,2024,50(11):70-77.
[20] 侯伟彬. 基于混合算法的受限空间电波覆盖特性研究[D]. 北京:北京交通大学,2019. HOU Weibin. Research on radio coverage characteristics in confined environment based on hybrid method[D]. Beijing:Beijing Jiaotong University,2019.
[21] 李大伟. 受限空间电波覆盖特性的研究[D]. 北京:北京交通大学,2016. LI Dawei. Research on the radio coverage characteristics in confined space[D]. Beijing:Beijing Jiaotong University,2016.
[22] 王树奇,房涛,郭枳彤. 矿井不同位置信源无线电波传播特性研究[J]. 煤炭技术,2010,29(3):186-188. WANG Shuqi,FANG Tao,GUO Zhitong. Propagation characteristic of radio waves in limited space of mine tunnels[J]. Coal Technology,2010,29(3):186-188.
[23] 成凌飞,曾文,史亚军. 矩形巷道电磁波传播混合模型分界点的研究[J]. 测控技术,2017,36(1):116-119. DOI: 10.3969/j.issn.1000-8829.2017.01.028 CHENG Lingfei,ZENG Wen,SHI Yajun. Research on division point of radio wave propagation hybrid model in rectangular tunnel[J]. Measurement & Control Technology,2017,36(1):116-119. DOI: 10.3969/j.issn.1000-8829.2017.01.028
[24] 成凌飞,卢超,鲍鑫行. 矩形巷道电磁波混合模型的模式数量研究[J]. 河南理工大学学报(自然科学版),2014,33(5):686-691. DOI: 10.3969/j.issn.1673-9787.2014.05.026 CHENG Lingfei,LU Chao,BAO Xinhang. Mode number of electromagnetic waves of hybrid model in rectangular tunnels[J]. Journal of Henan Polytechnic University (Natural Science),2014,33(5):686-691. DOI: 10.3969/j.issn.1673-9787.2014.05.026
[25] 官科. 轨道交通场景电波传播建模理论与方法研究[D]. 北京:北京交通大学,2014. GUAN Ke. Researches on wave propagation modeling theory and methodology in rail traffic scenarios[D]. Beijing:Beijing Jiaotong University,2014.
[26] 石庆冬,孙继平. 弯曲矩形隧道电磁波衰减特性[J]. 中国矿业大学学报,2001,30(1):91-93. DOI: 10.3321/j.issn:1000-1964.2001.01.022 SHI Qingdong,SUN Jiping. Attenuation characteristic of guided EM waves in curved rectangular mine tunnel[J]. Journal of China University of Mining & Technology,2001,30(1):91-93. DOI: 10.3321/j.issn:1000-1964.2001.01.022
[27] 李飞腾. 矩形弯曲隧道中电磁波传播特性研究[D]. 焦作:河南理工大学,2018. LI Feiteng. Research on the electromagnetic wave propagation characteristics in curved rectangular tunnel[D]. Jiaozuo:Henan Polytechnic University,2018.
[28] 孙继平,张长森. 列车对半圆拱形隧道中电磁波截止频率的影响[J]. 电波科学学报,2002,17(5):514-516,523. DOI: 10.3969/j.issn.1005-0388.2002.05.017 SUN Jiping,ZHANG Changsen. Study on the influence to the cutoff frequency of semicircle-tunnel from the train[J]. Chinese Journal of Radio Science,2002,17(5):514-516,523. DOI: 10.3969/j.issn.1005-0388.2002.05.017
[29] 孙继平,张长森. 圆形隧道中电磁波的传输特性[J]. 电波科学学报,2003,18(4):408-412. DOI: 10.3969/j.issn.1005-0388.2003.04.013 SUN Jiping,ZHANG Changsen. The propagation characteristic of electromagnetic wave in a round tunnel[J]. Chinese Journal of Radio Science,2003,18(4):408-412. DOI: 10.3969/j.issn.1005-0388.2003.04.013
[30] 薛少华,谭建平,邓积微,等. 矿井井筒中电磁波传播特性研究与无线通信试验[J]. 煤炭学报,2018,43(8):2361-2366. XUE Shaohua,TAN Jianping,DENG Jiwei,et al. Radio channel characterization study and wireless communication trial in mine shaft[J]. Journal of China Coal Society,2018,43(8):2361-2366.
[31] 孙继平,彭铭,刘斌. 矿井无线传输测试分析与矿用5G优选工作频段研究[J]. 工矿自动化,2024,50(10):1-11,20. SUN Jiping,PENG Ming,LIU Bin. Analysis of wireless transmission tests in mines and preferred working frequency bands for mining 5G[J]. Journal of Mine Automation,2024,50(10):1-11,20.
[32] NYCHIS G,LIU X. Wireless MAC protocols[EB/OL]. [2024-04-08]. http://www.cs.cmu.edu/~ srini/15-849/S06/lectures/06-mac-student.ppt.
[33] KAWADIA V,KUMAR P. Power control and clustering in ad hoc networks[C]. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies,San Francisco,2003:459-469.




 下载:
下载: