A multi-task allocation method for coal gangue sorting robots based on the integration of greedy strategy and scheduling rules
-
摘要:
煤炭复杂的原煤开采工艺与原煤含矸率变化导致带式输送机上矸石的到达率、位置坐标和粒度大小呈现非线性变化,影响煤矸分拣的综合收益。在综合考虑矸石队列特征与排队论调度规则的基础上,提出了贪心策略与调度规则融合的多机械臂煤矸分拣机器人多任务分配方法。构建包含匹配矩阵、效益矩阵和环境状态矩阵的多机械臂煤矸分拣机器人多任务分配基础框架。分析矸石队列各维度信息特点与部分调度规则机理,研究不同调度规则间的组合方法,建立调度规则组合集,通过贪心策略比较不同时间窗口内不同调度规则的综合收益,以煤矸分拣过程中的分拣率与任务完成成功率作为综合收益,按照综合收益最大来选择调度规则进行多任务分配。搭建不同最大过煤量的时变原煤流仿真环境,进行多机械臂煤矸分拣机器人多任务分配仿真实验,结果表明:对于最大过煤量120,150 kg/s的时变原煤流样本,采用贪心策略与调度规则融合的煤矸分拣机器人多任务分配方法时矸石分拣率分别为97.69%,89.10%,较单一调度规则方法分别提升6.82%,5.67%;任务完成成功率为95.64%,86.46%,较单一调度规则方法分别提升3.02%,2.13%;机械臂利用率标准差较小,表明该方法降低了原煤流时变性对煤矸分拣综合收益的影响。
Abstract:The complex raw coal mining process and the variation in the raw coal gangue content result in nonlinear changes in the arrival time, position coordinates, and particle size of the gangue on the belt conveyor, which affects the overall benefits of coal gangue sorting. Based on a comprehensive consideration of the gangue queue characteristics and queuing theory scheduling rules, a multi-task allocation method for coal gangue sorting robots, integrating a greedy strategy and scheduling rules, was proposed. A basic framework for multi-task allocation of multi-arm coal gangue sorting robots was constructed, including a matching matrix, benefit function matrix, and environmental state matrix. The characteristics of each dimension of the gangue queue information and the mechanisms of some scheduling rules were analyzed. The combination methods of different scheduling rules were studied, and a scheduling rule combination set was established. Through the greedy strategy, the overall benefits of different scheduling rules within different time windows were compared, with the sorting rate and task completion success rate in the coal gangue sorting process serving as the overall benefit rate. The scheduling rule that maximized the overall benefit was selected for multi-task allocation. A time-varying raw coal flow simulation environment with different maximum coal throughput was set up for multi-robot coal gangue sorting task allocation simulation experiments. The results showed that for time-varying raw coal flow samples with maximum coal throughput of 120 and 150 kg/s, the coal gangue sorting rates were 97.69% and 89.10%, respectively, when using the proposed multi-task allocation method with a greedy strategy and scheduling rules, which was an improvement of 6.82% and 5.67%, respectively, compared to the single scheduling rule method. The task completion success rates were 95.64% and 86.46%, respectively, showing improvements of 3.02% and 2.13%, respectively. The standard deviation of robot arm utilization was lower, indicating that the method reduced the impact of the time-varying raw coal flow on the overall benefits of coal gangue sorting.
-
0. 引言
煤矸石是煤矿开采过程中的有害废弃物,从煤中分离出煤矸石,提高原煤入选率,是煤炭工业绿色发展的重要指标[1-2]。传统洗选工艺存在高介耗、环境污染等问题[3],大型机械干选工艺存在分选效率低、成本高等问题[4]。采用机器人进行煤矸高效分拣,符合当前绿色环保发展趋势,成为主流研究方向[5-7]。煤矸分拣机器人关键技术包括煤矸识别与定位、动态目标跟踪、多机械臂协同控制等。基于深度学习的煤矸图像识别与定位算法在复杂工况下展现出高准确率和实时性[8]。动态目标跟踪技术解决了高速重载条件下矸石的精确拾取与放置问题[9]。多机械臂协同控制则通过机械臂同步操作,充分发挥前两者的技术优势[10]。要进一步提升分拣收益,关键在于实现多机械臂的高效任务分配,即在资源与时间限制条件下,将多项矸石分拣任务合理分配给多台机械臂执行,从而在现有技术基础上最大化机器人系统的分拣收益[11]。针对多机器人多任务分配问题,通常采用启发式算法[12-13]、市场机制方法[14]、基于聚类方法[15]等一般性方法,对于复杂环境下的煤矸分拣问题,存在任务分配用时长、环境适应性差等问题。
矸石在带式输送机上的分拣问题可归类为一种特殊的多动态目标跟踪与分配问题[16-17]。根据传统零件取放模型,矸石流在带式输送机上的初期任务分配遵循先来先服务(First in First Out,FIFO)原则[18],优先选择最先到达的矸石作为抓取目标。传统的机械臂矸石分拣任务分配方法无策略规划,矸石分拣率和机械臂利用率较低。对此,笔者团队首次提出了煤矸分拣机器人分拣策略[19],通过多机械臂协同工作方式,提高了一定含矸率下的矸石分拣率与机械臂利用率。董雅文等[20]提出了基于大粒度优先的煤矸分拣多机械臂任务分配策略,提高了原煤流中矸石粒度不统一条件下的分选率。Ma Hongwei等[21]提出了一种基于改进匈牙利算法的多臂全局协同煤矸石分选方法,解决了因机械手之间合作度低而导致的低分选率问题。Wang Peng等[22]提出了一种基于免疫空间的协同控制方法,提高了多机械臂工作空间不固定条件下的分选率。
在实际工况中,过煤量与含矸率受采煤设备、煤层赋存条件、煤层稳定性、开采方式及放煤工艺等多种因素的综合影响。由于煤层赋存条件的限制及地质条件的多样性,煤炭开采过程中常呈现过矸量的不均衡性[23-24]。煤矸分拣任务分配的复杂性随之增加。对于复杂多变环境下的多任务分配问题,王雯等[25]提出一种层次式任务规划法,在确保任务达成的同时,赋予方案灵活调整能力,从而提升效率,但在应对动态不确定性和信息不完备的任务场景时,需提高鲁棒性及有效性。王凡通等[26]针对自动仓储系统中多自动导引车批量搬运任务分配问题,提出了动态参数自适应调整策略,仿真实验结果表明,该策略提高了多自动导引车执行批量搬运任务的稳定性和鲁棒性,缩短了任务分配所用时间。
上述方法对复杂环境下的任务分配策略进行了优化,然而在应对原煤流时变性导致的矸石队列特征变化问题时,其应变能力略显不足。对此,本文根据煤矸分拣机器人的工作特征,建立煤矸分拣机器人多任务分配数学模型,通过多机械臂采用不同调度规则的方式,融合贪心策略,实现根据实际矸石队列选择最佳调度规则,提高机器人的分拣收益。
1. 煤矸分拣机器人多任务分配问题描述
1.1 煤矸分拣机器人分拣过程
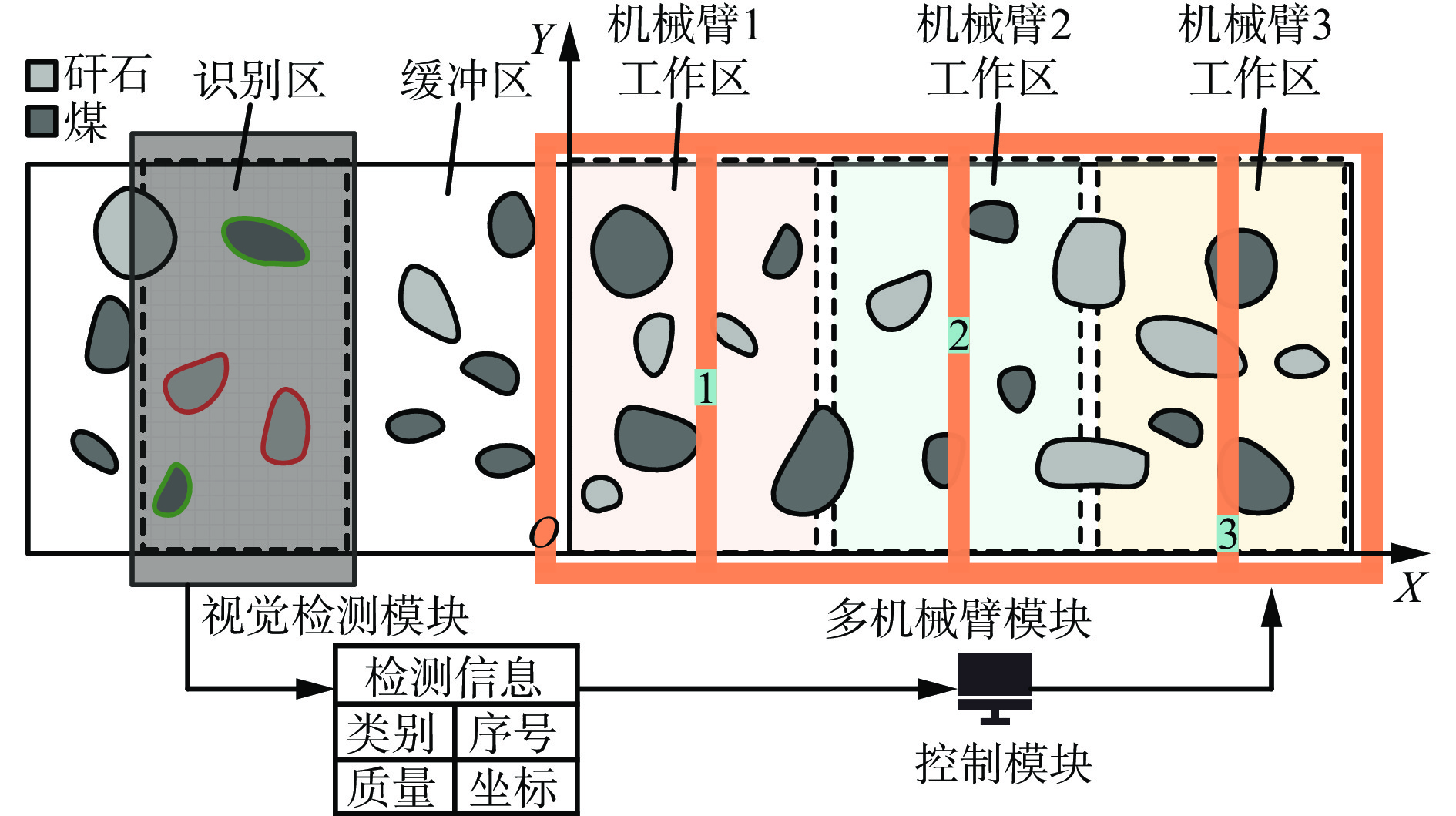
煤矸分拣机器人系统包括视觉检测模块、多机械臂模块与控制模块,如图1所示。视觉检测模块对经过识别区的原煤流进行煤与矸石的识别定位,由双目相机采集体积信息,结合密度得到质量信息,连同类别、序号、坐标信息发送至控制模块。缓冲区位于识别区与机械臂工作区之间,控制模块在矸石与煤离开缓冲区前完成任务分配。依照机械臂数量,划分相互独立的机械臂工作区,机械臂实际放置位置对应的工作区为其真实工作空间,不考虑机械臂放置位置的理论工作区为其逻辑工作空间。以原煤流进入多机械臂模块工作区方向,靠近机械臂初始位置的工作区起点为工作区起始点与坐标原点O,以带式输送机胶带运行方向为X轴,在胶带表面垂直于X轴且远离机械臂起始方向为Y轴,构建XOY坐标系。机械臂的抓取中心为工作区内的一个移动点,轨迹规划函数根据机械臂抓取中心坐标与矸石坐标规划机械臂运行轨迹。机械臂按照规划的轨迹抓取矸石并运送至回收区域,完成一次完整的分拣任务。
1.2 煤矸分拣机器人多任务分配假设条件
煤矸分拣机器人分配问题具有多任务性。在实际工况中,随着过矸量增加,分拣矸石的任务数量远大于机械臂数量,1台机械臂需要被分配多个分拣任务,但同一时刻只能完成1块矸石的分拣,因此需按照一定的顺序依次完成分拣任务,从而实现更高质量或更多数量的矸石分拣。矸石在带式输送机上不断运动,由于矸石位置发生变化,在不同时刻,机械臂完成同一任务所需的时间也是动态变化的。矸石队列模型包含空间、时间和特征3个维度的信息,其中:空间维度信息为矸石的X轴和Y轴坐标值,影响任务拾取和放置的时间;时间维度信息是矸石队列的到达时间间隔,影响任意时刻的任务数量;特征维度信息是任务的粒度信息,影响机械臂拾取和放置任务的质量收益。开采过程中矸石的粒度与位置分布具有一定随机性,与当前时刻的过矸量有关,原煤流中的过煤量及含矸率波动会引起过矸量持续变化。
煤矸分拣机器人多任务分配问题研究的核心在于如何提高多任务分配策略对环境变化的适应能力,从而快速应对原煤流中过矸量变化,实现更高质量或更多数量的矸石分拣。为了更好地描述煤矸分拣机器人多任务分配问题,不失一般性,作如下假设:
1) 带式输送机胶带匀速运动,无打滑、跑偏和松弛现象,煤和矸石与胶带表面始终为静摩擦。
2) 所有机械臂依照固定工作空间模式分布,即每台机械臂的工作空间固定且独立,工作时各机械臂之间不会发生物理干涉。
3) 在机械臂抓取矸石的过程中,将末端执行器和煤矸石视作移动点。机械臂完成抓取动作所需的时间总和只取决于末端执行器与目标矸石之间的相对位置,而与矸石和末端执行器的具体形状无关。
4) 机械臂在成功完成抓取动作后,需将矸石放置到指定的卸载位置,并回到初始位置,以准备进行下一次抓取任务。
5) 机械臂与主控机之间的通信稳定时间忽略不计。
6) 保证煤矸识别过程的有效性,能够准确识别并定位矸石。
1.3 煤矸分拣机器人多任务分配评价指标
将成功抓取与放置的矸石总质量与已检测矸石的总质量之比定义为分选率:
$$ {\varepsilon }_{{\mathrm{s}}}=\dfrac{\displaystyle \sum _{t}\displaystyle \sum _{k}{\gamma }_{k,t} {m}_{k}}{\displaystyle \sum _{t}\displaystyle \sum _{k}{m}_{k}}\quad 0\leqslant {\varepsilon }_{{\mathrm{s}}}\leqslant 1 $$ (1) 式中:γk,t为第k块矸石在任意时刻t下的分配结果,γk,t=1表示矸石已被抓取,γk,t=0表示矸石尚未被抓取;mk为第k块矸石的质量。
将成功抓取与放置的矸石总数量与已检测矸石的总数量之比定义为任务完成成功率:
$$ {\varepsilon }_{{\mathrm{f}}}=\dfrac{\displaystyle \sum _{t}\displaystyle \sum _{k}{\gamma }_{k,t}}{{N}_{{\mathrm{G}}}}\quad 0\leqslant {\varepsilon }_{{\mathrm{f}}}\leqslant 1 $$ (2) 式中NG为已检测的矸石总数量。
分选率与任务完成成功率共同构成煤矸分拣综合收益率,是对质量与数量的双重要求。
将机械臂实际工作时间与工作总时间的比值定义为机械臂的利用率:
$$ {\varepsilon _{{j}}} = {\dfrac{{\displaystyle {\sum _k}{t_{j,k}}}}{{{T_{{\mathrm{end}}}}}}}\quad{0 \leqslant {\varepsilon _{{j}}} \leqslant 1} $$ (3) 式中:tj,k为第j台机械臂抓取第k块矸石所用时间;Tend为工作总时间。
多机械臂间任务分配的均衡程度可用分选率的标准差表示。
2. 煤矸分拣机器人多任务分配模型
贪心策略与调度规则融合的煤矸分拣机器人多任务分配模型由煤矸分拣机器人多任务分配基础框架、部分调度规则选择及其组合方法、基于贪心策略的最优规则组合选择方法组成,如图2所示。
2.1 煤矸分拣机器人多任务分配基础框架
通过分析时变原煤流与矸石队列、机械臂与任务分配过程的映射关系,建立矸石队列模型。结合多机械臂模型,设计基于轨迹规划函数的判定矩阵、环境状态矩阵与状态转移函数,构建煤矸分拣机器人多任务分配基础框架。该框架以矸石队列作为输入,输出指定规则与策略下的任务分配结果。
矸石队列模型包含时间、空间和特征3个维度的关键信息,即
$$ {G_k} = \left\{ {{x_k},{y_k},{t_k},{m_k}} \right\}{\text{ }} $$ (4) 式中:Gk为第k块矸石的队列模型;(xk,yk)为第k块矸石在XOY平面的位置坐标,表示空间维度信息;tk为第k块矸石与第k−1块矸石的到达时间间隔,表示时间维度信息。
多机械臂模型为
$$ {M_j} = \left\{ {{A_j},{V_{{j}}},{P_j},{x_{{{\mathrm{a}}j}}},{y_{{{\mathrm{a}}j}}},{z_{{{\mathrm{a}}j}}},{T_{{{\mathrm{a}}j}}}} \right\} $$ (5) 式中:Aj为第j台机械臂可达到的最大加速度;Vj为第j台机械臂可达到的最大运行速度;Pj为第j台机械臂的工作状态,Pj=1表示机械臂处于忙碌状态,Pj=0表示机械臂处于空闲状态;(xaj,yaj)为第j台机械臂末端执行器抓取中心在工作空间的初始位置;zaj为第j台机械臂抓取时所需下降距离;Taj为第j台机械臂末端执行器开合所需时间。
根据机械臂初始位置、矸石位置、抓取方式等信息构建轨迹函数ftra(·)[27],得到机械臂最优抓取路径和所需时间。
第j台机械臂抓取第k块矸石所需时间为
$$ {t_{j,k}} = {{f}_{{\mathrm{tra}}}}({x_{{k}}},{y_{{k}}},{x_{{{\mathrm{a}}{{j}}}}},{y_{{{\mathrm{a}}{{j}}}}},{z_{{{\mathrm{a}}{{j}}}}},{{A}_{j}},{{V}_{j}},{V_{\mathrm{b}}},{T_{{{\mathrm{a}}{{j}}}}}) $$ (6) 式中Vb为带式输送机运行速度。
矸石离开机械臂工作区所需的时间需小于机械臂完成该块矸石分拣的时间才能完成抓取,定义sj,k为机械臂是否能够进行分拣的判定依据,sj,k=1表示第j台机械臂当前时刻满足对第k块矸石的抓取条件,sj,k=0表示第j台机械臂当前时刻不满足对第k块矸石的抓取条件。
$$ {s_{j,k}} = \left\{ {\begin{array}{*{20}{c}} 0&{{t_{j,k}} \geqslant \dfrac{{{x_{{{\mathrm{h}}j}}} - {x_k}}}{{{V_{\mathrm{b}}}}}} \\ 1&{{t_{j,k}} < \dfrac{{{x_{{{\mathrm{h}}j}}} - {x_k}}}{{{V_{\mathrm{b}}}}}} \end{array}} \right. $$ (7) 式中xhj为第j台机械臂工作空间末端X轴坐标。
定义rj,k为第k块矸石与第j台机械臂的匹配状态,Rt为t时刻矸石与机械臂匹配矩阵。当机械臂满足矸石抓取条件且处于空闲状态时,rj,k=1,否则rj,k=0。
$$ {{\boldsymbol{R}}_t} = \left[ {\begin{array}{*{20}{c}} {{r_{1,1}}} & {{r_{1,2}}} & \cdots & {{r_{1,k}}} \\ {{r_{2,1}}} & {{r_{2,2}}} & \cdots & {{r_{2,k}}} \\ \vdots & \vdots & {} & \vdots \\ {{r_{j,1}}} & {{r_{j,2}}} & \cdots & {{r_{j,k}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{s_{1,1}} {P_1}} & {{s_{1,2}} {P_1}} & \cdots & {{s_{1,k}} {P_1}} \\ {{s_{2,1}} {P_2}} & {{s_{2,2}} {P_2}} & \cdots & {{s_{2,k}} {P_2}} \\ \vdots & \vdots & {} & \vdots \\ {{s_{j,1}} {P_j}} & {{s_{j,2}} {P_j}} & \cdots & {{s_{j,k}} {P_j}} \end{array}} \right] $$ (8) 定义Ct为t时刻矸石分拣收益矩阵,cj,k为t时刻第k块矸石由第j台机械臂在某种调度规则下的分拣收益。不同调度规则计算收益的方式不同,如以矸石质量为调度规则评价指标时,cj,k为每块矸石的质量参数。
$$ {{\boldsymbol{C}}_t} = \left[ {\begin{array}{*{20}{c}} {{c_{1,1}}}&{{c_{1,2}}}& \cdots &{{c_{1,k}}} \\ {{c_{2,1}}}&{{c_{2,2}}}& \cdots &{{c_{1,k}}} \\ \vdots & \vdots & {}& \vdots \\ {{c_{j,1}}}&{{c_{j,2}}}& \cdots &{{c_{j,k}}} \end{array}} \right] $$ (9) 定义Et为多任务分配的环境状态矩阵,其元素为矸石与机械臂匹配矩阵和当前调度规则下矸石分拣收益矩阵的哈达玛积。Et为当前时刻及当前规则下,任意矸石指派由不同机械臂分拣的真实收益,其最值对应当前规则下分拣收益最大的矸石。
$$ {{\boldsymbol{E}}_t} = {{\boldsymbol{R}}_t} \odot {\boldsymbol{C}}_t = \left[ {\begin{array}{*{20}{c}} {{r_{1,1}} {c_{1,1}}}&{{r_{1,2}} {c_{1,2}}}& \cdots &{{r_{1,k}} {c_{1,k}}} \\ {{r_{2,1}} {c_{2,1}}}&{{r_{2,2}} {c_{2,2}}}& \cdots &{{r_{2,k}} {c_{2,k}}}\\ \vdots &\vdots & {} & \vdots \\ {{r_{j,1}} {c_{j,1}}}&{{r_{j,2}} {c_{j,2}}}& \cdots &{{r_{j,k}} {c_{j,k}}} \end{array}} \right] $$ (10) 设faction(·)为多任务分配模型中机械臂对矸石的选择过程,Q为当前规则下对于环境状态矩阵的选择方法。不同调度规则计算多任务分配的方法不同,如以矸石质量为调度规则评价指标时,依次选择环境状态矩阵中每列的最大值并在其余列中剔除该值对应的矸石作为分配结果。
$$ {U_t} = {f_{{\mathrm{action}}}}({{\boldsymbol{E}}_t},{{Q}}) $$ (11) 式中Ut为当前时刻下的多任务分配结果。
多机械臂完成任务所需时间不同,采用固定时间间隔Tq进行环境状态更新。
$$ \left\{ {\begin{gathered} {{t_{\mathrm{s}}} = {t_{j,k}} - t {T_{\mathrm{q}}}} \\ {x_k^\prime = {x_k} + t {T_{\mathrm{q}}} {V_{\mathrm{b}}}} \\ \end{gathered}} \right. $$ (12) 式中:ts为机械臂完成当前任务剩余时间;$ x_k' $为更新后的矸石X轴坐标。
根据Pj与xk的变化重新计算矸石分拣的匹配矩阵及收益矩阵,更新环境状态矩阵,进行状态转移,直至矸石队列全部完成分拣或离开工作区。
2.2 部分调度规则选择及其组合方法
通过研究矸石队列特征与调度规则机理,根据煤矸分拣机器人机械臂之间的协同关系进行调度规则组合。
2.2.1 调度规则选择
当前时刻进入工作区的矸石个数即为矸石数量,其值变化相当于任务量突然增加或减少,影响当前时刻多机械臂拾取和放置矸石的丢失率。矸石粒度影响机械臂拾取和放置的效益。矸石队列的X轴和Y轴坐标影响机械臂拾取和放置矸石的时间。
对应矸石进入工作区的序号、时间和质量,采用FIFO、最大质量优先(Mass First,MF)和最短时间优先(Shortest Processing Time,SPT)作为煤矸分拣机器人多任务分配模型的基础规则。其中FIFO规则是按照任务的到达时间顺序进行处理;MF规则是按照任务的质量效益顺序进行处理,可以优先分拣质量较大的矸石来最大化分选率;SPT规则是优先处理耗时最短的任务,从而加快整体处理速度,提高系统的吞吐量。
调整矸石分拣收益函数为不同调度规则下的分拣收益。
$$ c_{ j, k}^\theta= \begin{cases} 1-\dfrac{t_{j, k}}{\max t_{j, k}} & \theta=1 \\ \dfrac{m_k}{\max m_k} & \theta=2 \\ 1-\dfrac{k}{n_{\mathrm{s}}} & \theta=3\end{cases} $$ (13) 式中:$ c_{ j, k}^\theta $为第j台机械臂对第k块矸石执行规则θ的分拣收益,θ=1,2,3,分别表示STP,MF,FIFO规则;ns为当前矸石队列中矸石总数量。
2.2.2 调度规则组合
在任务分配模型中,单一、无差异化的调度规则使算法复杂度低且易于部署。但当多台机械臂同时执行任务时,由于矸石队列不断变化,可能会对综合收益产生不利影响。如果能为不同机械臂分配多种调度规则,则可以充分利用每种规则的优势,从而显著提升整体分拣效率与收益。
视每台机械臂为独立个体,可自由选择调度规则执行任务。若以机械臂实际工作空间顺序为机械臂分配调度规则,只有在前端机械臂完成工作空间内的矸石分拣任务后,后端机械臂才能处理剩余矸石,且其选择的空间远小于前端机械臂,限制了多台机械臂的并行性和灵活性,可能导致部分机械臂闲置或处理效率较低的情况。针对该问题,对多台机械臂的工作空间进行逻辑重构,以逻辑层面融合方式进行任务分配,如图3所示,使各机械臂不再局限于物理上的独立工作区域。图3中,Ⅰ,Ⅱ,Ⅲ分别为机械臂1,2,3的工作空间,T1,T2,T3分别为同一矸石队列进入机械臂1,2,3工作空间的时刻。在同一工作空间内,机械臂按照红—绿—蓝虚线的顺序进行任务分配,序号①—⑤表示多机械臂选择矸石的顺序。该方式按矸石队列进入不同机械臂工作空间的时刻进行融合,形成一个多时间维度下的工作空间。由于时间维度不同,机械臂之间协同并行作业时不会发生干涉。当前时刻下任意机械臂处于空闲状态时,都可针对工作空间内的剩余矸石进行分拣任务分配,通过该方式弱化机械臂顺序对抓取结果带来的影响,发挥调度组合的优势。
定义forder(·)为机械臂顺序选择函数,S1,S2,S3分别对应机械臂初次被赋予的调度规则(FIFO,MF,SPT)。在首次执行分配任务时,按照随机算法决定机械臂的初次分配顺序,即
$$ {f_{{\mathrm{order}}}}({S_1},{S_2},{S_3}) = {\text{random}}({S_1},{S_2},{S_3}) $$ (14) 式中random(·)为随机打乱内部元素顺序的函数。
以FIFO−MF−SPT规则组合为例,假设随机分配后机械臂物理序号对应的规则顺序为SPT−FIFO−MF,将当前时刻矸石与机械臂匹配状态乘以机械臂对应规则下的收益,得到当前规则组合下的环境状态矩阵:
$$ {{\boldsymbol{E}}_{{t}}} = \left[ {\begin{array}{*{20}{c}} {{r_{1,1}} c_{1,1}^1}& r_{1,2}c_{1,2}^1 & \cdots &{{r_{1,k}} c_{1,k}^1} \\ {{r_{2,1}} c_{2,1}^3}& r_{2,2}c_{2,2}^3 & \cdots &{{r_{2,k}} c_{2,k}^3} \\ {{r_{3,1}} c_{3,1}^2}& r_{3,2}c_{3,2}^2 & \cdots &{{r_{3,k}} c_{3,k}^2} \end{array}} \right] $$ (15) 当前规则组合下对于环境状态矩阵的选择方法为从矩阵Et第1行中选择最大值,其序号k对应第1台机械臂当前时刻下应分拣的矸石,记Gq1=Gk,同时更新第1台机械臂当前工作时间为抓取第k块矸石所用的时间,并在第2行中将该块矸石所对应的r2,k置0。当最大值为0时,当前机械臂处于忙碌状态或无对应可分拣矸石。找到该矩阵所有行中最大值及其对应的矸石序号后,通过煤矸分拣机器人多任务分配数学模型,更新$ {\boldsymbol{E}}_t $直至矸石队列离开工作区。统计所有已完成任务分配的矸石与任务分配时刻,作为该规则组合下的多任务分配结果。
2.3 基于贪心策略的最优规则组合选择方法
依照贪心策略思想,将矸石队列分解为时间窗口,根据综合收益最大化的原则,选择每个窗口下的最佳规则组合,并将环境变化与机械臂状态传递到下一时间窗口,实现连续的多任务优化分配。
原煤流具有时变性,导致矸石队列分布特征不断发生变化。采用固定不变的规则组合难以抑制其带来的影响,导致综合收益率较低。本文采用贪心策略思想,将原煤流分解为若干个时间窗口,分别求解各个时间窗口内所有规则组合下的分配结果,选择综合收益率最高的规则组合作为该窗口下任务分配规则,通过计算局部最优值的方式来提高整体的综合收益率。
实际工况中,带式输送机不断运输煤与矸石进入机械臂工作区内,分解后的各个时间窗口在空间维度上首尾紧密相连,不存在间隔。当任意时间窗口下原煤流完全离开机械臂工作区时,下一时间窗口内已有部分煤流进入机械臂工作空间,因此无法直接在每个时间窗口独立地采用煤矸分拣机器人多任务分配基础框架进行任务分配。由于原煤流在离开机械臂工作空间的过程中,未抓取矸石与机械臂的初始位置越来越远,所需的分拣时间随之增加,此时SPT规则在进行任务分配时,若只计算原煤流尾部即将离开机械臂工作区的矸石分拣时间,忽略下一时间窗口中已经进入机械臂工作区的部分矸石,会降低SPT规则因选择耗时最短任务而带来的效率优势。基于贪心策略的最优规则组合选择方法中,将从时间窗口中原煤流首段进入机械臂工作区到尾端进入机械臂工作区作为一个任务分配的计算区间,当在一个时间窗口内完成任务分配计算时,将该时间窗口内机械臂工作区剩余的煤流并入下一时间窗口的首部,并将此时的机械臂工作状态作为下一时间窗口的机械臂初始状态,完成时间窗口间的连接。每个时间窗口内进行任务分配过程迭代的实际工作时间为
$$ {t_{\mathrm{d}}} = \frac{{{L_{\text{c}}}}}{{{V_{\mathrm{b}}}}} $$ (16) 式中Lc为时间窗口所包含的原煤流总长度。
对于初始时间窗口,分别计算其在不同调度规则组合下的分配结果UJ,其中J为当前调度规则组合序号。计算各组分配结果下的分拣率与任务完成成功率,根据评价指标(质量优先或数量有限)选择最佳任务分配结果Ubest。
$$ {U}_{{\mathrm{best}}}=\max(\alpha {\varepsilon }_{{\mathrm{s}}}^{},(1-\alpha ) {\varepsilon }_{{\mathrm{f}}}^{}) $$ (17) 式中α为评价指标权重系数,α=1时以分拣矸石总质量优先,α=1时以分拣矸石总数量优先。
当出现相同综合收益率时,优先选择机械臂剩余工作时间较短的规则组合。对于后续时间窗口,在完成原煤流与机械臂初始化参数修正后,进行与初始时间窗口内相同的计算过程。
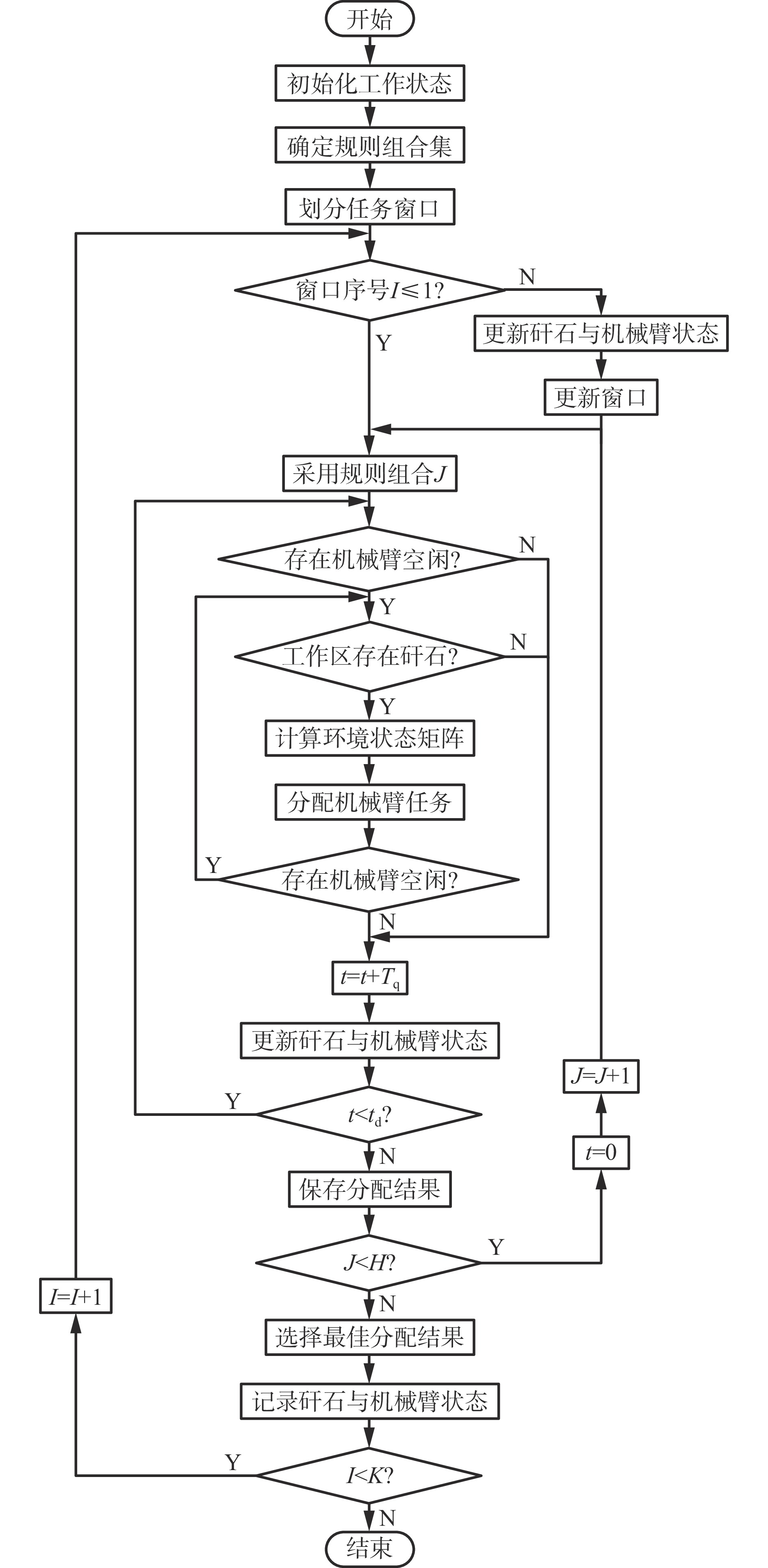
2.4 煤矸分拣机器人多任务分配流程
贪心策略与调度规则融合的煤矸分拣机器人多任务分配流程如图4所示。I为当前窗口序号,K为窗口总数,H为调度规则组合总数。
在原煤流进入视觉检测模块前,进行各参数初始化,确认调度规则组合的总数及内容。之后对已识别的原煤流,按照指定长度划分为若干个矸石队列。若存在空闲机械臂与可分拣矸石,则按照1号调度规则组合进行分拣,并更新时间参数,直至时间参数大于窗口通过机械臂工作区的总时间。重复上述步骤,采用下一序号调度规则组合进行运算,直至应用所有的调度规则组合。选择最佳调度规则组合下的任务分配结果,对下一窗口的矸石队列进行更新,直至原煤流完全通过机械臂工作区,结束任务分配过程。
3. 煤矸分拣机器人多任务分配实验
为验证贪心策略与调度规则融合的煤矸分拣机器人多任务分配方法能有效提高煤矸分拣机器人对时变原煤流的综合收益率与任务分配均衡性,采用3种不同最大过煤量的样本进行实验,统计并计算全部样本的矸石分拣率、任务完成成功率。
实验设置:原煤流最大过煤量分别为90,120,150 kg/s;带式输送机运行速度为0.5 m/s;3台机械臂最大运行速度均为6 m/s,加速度为4 m/s2;矸石粒度为50~300 mm,符合泊松分布;矸石到达时间遵循指数分布特性,具有随机性;以叠加噪声信号的正弦函数来模拟含矸率的动态变化特征,确保实验条件贴近实际工况中的复杂性与不确定性。在煤矸分拣机器人多任务分配基础框架中,单独使用FIFO,MF,SPT规则定义为单一调度规则方法。不同调度规则组合序号见表1。各组实验的过煤量和过矸量随时间变化曲线如图5所示。
表 1 不同调度规则组合序号Table 1. Corresponding sequence numbers of different scheduling rule combination序号 规则组合 序号 规则组合 1 FIFO−MF−SPT 6 FIFO−FIFO−SPT 2 FIFO−FIFO−FIFO 7 FIFO−MF−MF 3 MF−MF−MF 8 FIFO−SPT−SPT 4 SPT−SPT−SPT 9 MF−SPT−SPT 5 FIFO−FIFO−MF 10 MF−MF−SPT 实验过程中,采取10 m作为1个时间窗口长度。将本文方法与单一调度规则、最佳规则组合(由部分调度规则选择及组合得到)、基于贪婪算法的自适应权重(An Adaptive Weights Rule Based on Greedy Algorithm,GAW)方法[28]进行对比,多任务分配结果如图6所示。可看出在低过煤量条件下,各方法的综合收益差异不显著。随着最大过煤量增加,单一调度规则下的综合收益远低于其他方法,GAW方法下的综合收益略高于最佳调度规则组合方法,而本文方法的分拣效果最好。对于最大过煤量为120,150 kg/s的时变原煤流样本,采用本文方法时分拣率分别为97.69%,89.10%,较单一规则方法分别提升6.82%,5.67%;任务完成成功率为95.64%,86.46%,较单一规则方法分别提升3.02%,2.13%。
从不同过煤量实验样本中分别随机抽取10份矸石样本,统计本文方法在各时间窗口中对不同调度规则组合的选择次数,以热力图的形式呈现,如图7所示。
从图7可看出,当最大过煤量较低(90 kg/s)时,本文方法对不同规则组合的选择次数基本相同,表明不同规则组合的分拣效果差异不显著。当最大过煤量增加至120 kg/s,以分拣率为评价指标时,SPT−SPT−SPT,MF−SPT−SPT,MF−MF−SPT规则的选择次数略高于其他规则组合,FIFO−FIFO−MF,FIFO−MF−MF规则选择次数较少,各规则组合的选择次数出现一定差异;以任务完成成功率为评价指标时,SPT−SPT−SPT规则组合的选择次数显著多于其他规则,MF−SPT−SPT规则选择次数相对较多。当最大过煤量增加至150 kg/s,以分拣率为评价指标时,SPT−SPT−SPT规则及MF−SPT−SPT组合的选择次数显著多于其他组合,而FIFO−FIFO−MF组合的选择次数相对较少;以任务完成成功率为评价指标时,SPT−SPT−SPT组合的选择次数明显多于其他组合。
不同方法的机械臂利用率标准差见表2。该值越小,说明机械臂之间的任务分配越均衡。可看出单一调度规则方法的机械臂利用率标准差随着最大过煤量增加而减小,但仍远大于最佳调度规则组合方法与本文方法。后2种方法的机械臂利用率标准差均小于0.01,说明各机械臂之间的利用率相差较小,任务分配较均衡。
表 2 不同方法的机械臂利用率标准差Table 2. Standard deviation of robotic arm utilization for different methods多任务分配方法 不同最大过煤量时机械臂利用率标准差 90 kg/s 120 kg/s 150 kg/s 单一调度规则方法 0.035 6 0.027 3 0.017 2 最佳调度规则组合方法 0.007 6 0.007 6 0.009 9 本文方法 0.007 4 0.007 9 0.008 6 实验结果表明,本文方法在一定程度上提高了煤矸分拣综合收益,且平衡了各机械臂间的工作量。
4. 结论
1) 提出一种贪心策略与调度规则融合的多机械臂煤矸分拣机器人多任务分配方法,从排队论调度规则和原煤流时变性的角度出发,分析矸石质量、分拣时间等因素对分拣收益的影响,构建了多机械臂煤矸分拣机器人多任务分配基础框架;建立部分调度规则组合集;通过贪心策略求解不同时间窗口内多机械臂执行不同调度规则的综合收益。
2) 对不同最大过煤量下的时变原煤流进行实验验证,结果表明所提方法对于最大过煤量120 kg/s与150 kg/s的时变原煤流样本,分拣率分别达到97.69%,89.10%,任务完成成功率分别达到95.64%,86.46%。同时机械臂利用率的标准差较小,降低了原煤流时变性对煤矸分拣综合收益的影响。
-
表 1 不同调度规则组合序号
Table 1 Corresponding sequence numbers of different scheduling rule combination
序号 规则组合 序号 规则组合 1 FIFO−MF−SPT 6 FIFO−FIFO−SPT 2 FIFO−FIFO−FIFO 7 FIFO−MF−MF 3 MF−MF−MF 8 FIFO−SPT−SPT 4 SPT−SPT−SPT 9 MF−SPT−SPT 5 FIFO−FIFO−MF 10 MF−MF−SPT 表 2 不同方法的机械臂利用率标准差
Table 2 Standard deviation of robotic arm utilization for different methods
多任务分配方法 不同最大过煤量时机械臂利用率标准差 90 kg/s 120 kg/s 150 kg/s 单一调度规则方法 0.035 6 0.027 3 0.017 2 最佳调度规则组合方法 0.007 6 0.007 6 0.009 9 本文方法 0.007 4 0.007 9 0.008 6 -
[1] 刘峰,郭林峰,赵路正. 双碳背景下煤炭安全区间与绿色低碳技术路径[J]. 煤炭学报,2022,47(1):1-15. LIU Feng,GUO Linfeng,ZHAO Luzheng. Research on coal safety range and green low-carbon technology path under the dual-carbon background[J]. Journal of China Coal Society,2022,47(1):1-15.
[2] 金向阳,李杨,于雷,等. 煤矿区绿色低碳评价指标构建及应用[J]. 煤炭科学技术,2024,52(4):131-142. DOI: 10.12438/cst.2023-1806 JIN Xiangyang,LI Yang,YU Lei,et al. Construction and application of green and low-carbon evaluation indicators for coal mining areas[J]. Coal Science and Technology,2024,52(4):131-142. DOI: 10.12438/cst.2023-1806
[3] MIJAŁ W,TORA B. Development of dry coal gravity separation techniques[J]. IOP Conference Series:Materials Science and Engineering,2018,427(1). DOI: 10.1088/1757-899X/427/1/012003.
[4] 王鹏,曹现刚,夏晶,等. 基于机器视觉的多机械臂煤矸石分拣机器人系统研究[J]. 工矿自动化,2019,45(9):47-53. WANG Peng,CAO Xiangang,XIA Jing,et al. Research on multi-manipulator coal and gangue sorting robot system based on machine vision[J]. Industry and Mine Automation,2019,45(9):47-53.
[5] 侯晓松,李强. 智能机器人系统在煤矸分选工艺中的研究与应用[J]. 中国煤炭,2024,50(9):92-98. HOU Xiaosong,LI Qiang. Research and application of intelligent robot system in coal gangue sorting process[J]. China Coal,2024,50(9):92-98.
[6] ZHAO Guozhen,CHANG Fengyi,CHEN Jiaxin,et al. Research and prospect of underground intelligent coal gangue sorting technology:a review[J]. Minerals Engineering,2024,215. DOI: 10.1016/J.MINENG.2024.108818.
[7] JIANG Zhigang,HE Kunzhong,ZHANG Dongming. A review of intelligent coal gangue separation technology and equipment development[J]. International Journal of Coal Preparation and Utilization,2024,44(9):1308-1324.
[8] 李德永,王国法,郭永存,等. 基于CFS−YOLO算法的复杂工况环境下煤矸图像识别方法[J]. 煤炭科学技术,2024,52(6):226-237. DOI: 10.12438/cst.2023-1967 LI Deyong,WANG Guofa,GUO Yongcun,et al. Image recognition method of coal gangue in complex working conditions based on CES-YOLO algorithm[J]. Coal Science and Technology,2024,52(6):226-237. DOI: 10.12438/cst.2023-1967
[9] 朱子祺,李创业,代伟. 基于G−RRT*算法的煤矸石分拣机器人路径规划[J]. 工矿自动化,2022,48(3):55-62. ZHU Ziqi,LI Chuangye,DAI Wei. Path planning of coal gangue sorting robot based on G-RRT* algorithm[J]. Journal of Mine Automation,2022,48(3):55-62.
[10] WU Qihan,LI Meng,QI Xiaozhi,et al. Coordinated control of a dual-arm robot for surgical instrument sorting tasks[J]. Robotics and Autonomous Systems,2019,112:1-12. DOI: 10.1016/j.robot.2018.10.007
[11] 张烨,马宏伟,王鹏,等. 煤矸石智能分拣机器人研究进展与关键技术[J]. 工矿自动化,2022,48(12):42-48,56. ZHANG Ye,MA Hongwei,WANG Peng,et al. Research progress and key technologies of intelligent coal-gangue sorting robot[J]. Journal of Mine Automation,2022,48(12):42-48,56.
[12] 邓辅秦,黄焕钊,谭朝恩,等. 结合遗传算法和滚动调度的多机器人任务分配算法[J]. 计算机应用,2023,43(12):3833-3839. DENG Fuqin,HUANG Huanzhao,TAN Chao′en,et al. Multi-robot task allocation algorithm combining genetic algorithm and rolling scheduling[J]. Journal of Computer Applications,2023,43(12):3833-3839.
[13] 薛舒心,马亚杰,姜斌,等. 基于联盟形成博弈的异构无人机集群分布式任务分配算法[J]. 中国科学:信息科学,2024,54(11):2657-2673. XUE Shuxin,MA Yajie,JIANG Bin,et al. Distributed task allocation algorithm for heterogeneous unmanned aerial vehicle swarm based on coalition formation game[J]. Scientia Sinica(Informationis),2024,54(11):2657-2673.
[14] 翟政,何明,徐鹏,等. 基于市场机制的无人集群任务分配研究综述[J]. 计算机应用研究,2023,40(7):1921-1928. ZHAI Zheng,HE Ming,XU Peng,et al. Research review of task allocation for unmanned swarm based on market mechanism[J]. Application Research of Computers,2023,40(7):1921-1928.
[15] 刘占省,杨煜垚,史国梁. 融合聚类算法与改进哈里斯鹰算法的建筑机器人任务分配方法[J]. 建筑结构,2024,54(20):89-97,42. LIU Zhansheng,YANG Yuyao,SHI Guoliang. Improved Harris Hawk algorithm combined with clustering algorithm for task assignment of construction robots[J]. Building Structure,2024,54(20):89-97,42.
[16] 李卓,徐哲,陈昕,等. OTAP:基于预测的机会群智感知多任务在线分配算法[J]. 工程科学与技术,2018,50(5):176-182. LI Zhuo,XU Zhe,CHEN Xin,et al. OTAP:online multi-task assignment algorithm with prediction for opportunistic crowd sensing[J]. Advanced Engineering Sciences,2018,50(5):176-182.
[17] WANG Wenfei,LYU Maolong,RU Le,et al. Multi-UAV unbalanced targets coordinated dynamic task allocation in phases[J]. Aerospace,2022,9(9). DOI: 10.3390/AEROSPACE9090491.
[18] NOV Y,WEISS G,ZHANG Hanqin. Fluid models of parallel service systems under FCFS[J]. Operations Research,2022,70(2):1182-1218. DOI: 10.1287/opre.2021.2102
[19] 曹现刚,吴旭东,王鹏,等. 面向煤矸分拣机器人的多机械臂协同策略[J]. 煤炭学报,2019,44(增刊2):763-774. CAO Xiangang,WU Xudong,WANG Peng,et al. Collaborative strategy of multi-manipulator for coal-gangue sorting robot[J]. Journal of China Coal Society,2019,44(S2):763-774.
[20] 董雅文,孙家祺,张宝锋,等. 煤矸分拣多机械臂任务分配问题研究[J]. 煤炭工程,2024,56(1):170-176. DONG Yawen,SUN Jiaqi,ZHANG Baofeng,et al. Study on task allocation for multiple manipulators of coal gangue sorting[J]. Coal Engineering,2024,56(1):170-176.
[21] MA Hongwei,WEI Xiaorong,WANG Peng,et al. Multi-arm global cooperative coal gangue sorting method based on improved Hungarian algorithm[J]. Sensors,2022,22(20). DOI: 10.3390/S22207987.
[22] WANG Peng,MA Hongwei,ZHANG Ye,et al. A cooperative strategy of multi-arm coal gangue sorting robot based on immune dynamic workspace[J]. International Journal of Coal Preparation and Utilization,2023,43(5):794-814. DOI: 10.1080/19392699.2022.2078808
[23] 黄炳香,刘长友,程庆迎. 低位综放开采顶煤放出率与含矸率的关系[J]. 煤炭学报,2007,32(8):789-793. DOI: 10.3321/j.issn:0253-9993.2007.08.002 HUANG Bingxiang,LIU Changyou,CHENG Qingying. Relation between top-coal drawing ratio and refuse content for fully mechanized top coal carving[J]. Journal of China Coal Society,2007,32(8):789-793. DOI: 10.3321/j.issn:0253-9993.2007.08.002
[24] 朱帝杰,陈忠辉. 综放开采顶煤采出率预测模型的构建与应用[J]. 煤炭学报,2019,44(9):2641-2649. ZHU Dijie,CHEN Zhonghui. A model for top coal recovery ratio assessment and its application in longwall top coal caving[J]. Journal of China Coal Society,2019,44(9):2641-2649.
[25] 王雯,赵凯南,杨林,等. 面向复杂场景的层次式任务规划方法[J/OL]. 系统工程与电子技术:1-13[2025-01-02]. http://kns.cnki.net/kcms/detail/11.2422.TN.20241010.0913.004.html. WANG Wen,ZHAO Kainan,YANG Lin,et al. A hierarchical task planning approach for complex environments[J/OL]. Systems Engineering and Electronics:1-13[2025-01-02]. http://kns.cnki.net/kcms/detail/11.2422.TN.20241010.0913.004.html.
[26] 王凡通,王凌,高雁凤,等. 基于改进NSGA−Ⅱ算法的多AGV多任务分配研究[J]. 现代电子技术,2024,47(9):157-163. WANG Fantong,WANG Ling,GAO Yanfeng,et al. Research on multi-AGV multi-task allocation based on improved NSGA-Ⅱalgorithm[J]. Modern Electronics Technique,2024,47(9):157-163.
[27] 王鹏,曹现刚,马宏伟,等. 基于余弦定理−PID的煤矸石分拣机器人动态目标稳准抓取算法[J]. 煤炭学报,2020,45(12):797-804. WANG Peng, CAO Xiangang, MA Hongwei, et al. Dynamic target steady and accurate grasping algorithm of gangue sorting robot based on cosine theorem-PID[J]. Journal of China Coal Society, 2020, 45(12): 4240-4247.
[28] WU Xudong,CAO Xiangang,WANG Peng,et al. Multi-task allocation framework of coal gangue sorting robot system for the time-varying raw coal flow[J]. International Journal of Coal Preparation and Utilization,2024,44(6):715-739. DOI: 10.1080/19392699.2023.2217657



 下载:
下载: