Decision-making method for residual support force of hydraulic supports during pressurized moving under fragmented roof conditions in ultra-thin coal seams
-
摘要:
在破碎顶板条件下，液压支架带压移架过程中残余支撑力的精准决策对于提高极薄煤层智能化开采效率和保障作业安全至关重要。为实现极薄煤层破碎顶板条件下液压支架带压移架残余支撑力的准确决策，提出了一种基于改进蜣螂算法（IDBO）优化深度混合核极限学习机（DHKELM）的液压支架带压移架残余支撑力决策方法。在混合核极限学习机（HKELM）基础上引入极限学习机自动编码器（ELM−AE）结构来构建DHKELM模型，以增强对复杂输入的特征提取和非线性映射能力；引入ICMIC混沌映射、Lévy飞行和贪婪策略对蜣螂算法（DBO）进行改进，形成具备更高寻优精度和更快收敛速度的IDBO算法；利用IDBO算法优化DHKELM模型的超参数，建立IDBO−DHKELM模型。结合极薄煤层综采工作面液压支架带压移架实测数据，通过可视化和相关性分析，确定支架号、带压移架前支架支撑力、推移油缸进液压力和推移油缸行程变化速度作为影响残余支撑力的关键特征，并构建残余支撑力决策样本数据集，最终完成IDBO−DHKELM模型的训练与评估。实验结果表明：基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策结果的均方根误差（RMSE）、平均绝对误差（MAE）及决定系数（R2）分别为0.143，0.119，0.971，具有较高的决策精确度。
Abstract:Accurate decision-making on the residual support force of hydraulic supports during pressurized moving under fragmented roof conditions is crucial for improving intelligent mining efficiency in ultra-thin coal seams and ensuring operational safety. To address this challenge, this study proposed a novel decision-making method based on a Deep Hybrid Kernel Extreme Learning Machine (DHKELM) optimized by an Improved Dung Beetle Optimization (IDBO) algorithm. The DHKELM model was constructed by incorporating an Extreme Learning Machine Autoencoder (ELM-AE) into the Hybrid Kernel Extreme Learning Machine (HKELM) framework, enhancing its feature extraction capability and nonlinear mapping efficiency for complex inputs. Furthermore, the Dung Beetle Optimization (DBO) algorithm was enhanced with ICMIC chaotic mapping, Lévy flight, and a greedy strategy, yielding the IDBO algorithm with improved optimization accuracy and faster convergence. The IDBO algorithm was further employed to optimize the hyperparameters of the DHKELM model, forming the IDBO-DHKELM model. Using field-measured data from hydraulic supports during pressurized moving in a fully mechanized ultra-thin coal seam mining face, key influencing factors of residual support force—including support number, support force before pressurized moving, pushing cylinder inlet pressure, and pushing cylinder stroke variation speed—were identified through visualization and correlation analysis. A residual support force decision-making dataset was subsequently constructed, and the IDBO-DHKELM model was trained and evaluated. Experimental results demonstrate that the proposed IDBO-DHKELM model achieves high decision-making accuracy, with a root mean square error (RMSE) of 0.143, a mean absolute error (MAE) of 0.119, and a coefficient of determination (R2) of 0.971.
-
0. 引言
随着煤炭工业的高速发展，厚及中厚煤层的易开采资源逐渐减少，极薄煤层开采比重逐渐增加[1-2]。但极薄煤层开采面临开采空间狭小、工人劳动强度大、开采效率低、智能化程度不足等问题[3]。推动极薄煤层的安全、高效、智能开采对保障我国能源安全具有重要战略意义[4]。
液压支架作为极薄煤层综采的核心支护设备，其智能化水平对实现极薄煤层智能化开采至关重要[5-6]。在破碎顶板条件下，液压支架需采用带压移架方式跟机作业。为确保支架顶梁持续对破碎顶板提供稳定支撑，立柱底腔需保持一定的残余支撑力，并且残余支撑力的精确调控直接关系到顶板的支护效果和支架的跟机效率。然而，目前基于固定时间的液压支架自动跟机控制方式难以对破碎顶板条件下的残余支撑力准确调节，常导致支架带压移架失败，仍依赖人工进行跟机移架。对于极薄煤层工作面，这不仅极大增加了工人劳动强度和作业风险，还降低了移架效率，无法满足安全、高效、智能开采需求。因此，在破碎顶板条件下，如何实现液压支架自主跟机带压移架过程中残余支撑力的精准决策与自适应调控，对于极薄煤层的智能化开采、提高开采效率及保障作业安全具有重要意义[7-8]。
针对液压支架带压移架跟机技术，已有众多学者展开了相关研究，主要包括带压移架控制策略和残余支撑力理论分析等方面。在带压移架控制策略方面，牛剑峰[9]提出了一种与破碎顶板条件耦合的液压支架跟机控制策略，即通过压力传感器监测顶板卸压状况及行程传感器判断支架拉动可能性的耦合控制策略。付翔等[10]针对综采工作面复杂场景下液压支架人机交互协作任务需求，设计了液压支架中部跟机多模态人机协同控制系统，实现了不同顶板条件下的多模态控制。朱金雨等[11]设计了一种通过压力与时间双向判断的液压支架自动化跟机系统，实现了带压移架的有序控制。韩宝珠等[12]提出了一种基于PLC的液压支架带压移动控制方案，利用PLC和传感器技术，提升了液压支架带压移架的可靠性。在残余支撑力理论分析方面，杨科等[13]推导出了在大倾角条件下带压移架的临界值，为支架失稳分析提供了理论依据。张武等[14]基于液压支架液压系统的工作原理，利用AMESim软件进行仿真分析，探讨了泵站供液流量和主进回液管径对支架带压移架速度的影响。曹连民等[15]建立了液压支架带压移架的力学模型，分析了带压移架过程中的残余支撑力范围，并设计了相应的带压移架控制回路。李志旭[16]通过对液压支架带压移架过程进行力学特性分析，确定了立柱底腔的残余支撑力范围，并开展了液压支架力学分析计算。上述研究在液压支架带压移架跟机技术方面取得了一定进展，但现有的控制策略相对固化单一，未充分考虑复杂开采环境中残余支撑力与顶板压力、推移油缸进液压力等因素间的强耦合性及非线性关系。因此，实现带压移架残余支撑力的精准决策是一个复杂的难题。近年来，基于机器学习的数据驱动智能决策方法在煤矿开采领域逐渐兴起，凭借其强大的特征提取和非线性拟合能力，机器学习算法已广泛应用于矿压预测[17]和瓦斯预测[18]等任务中，这为带压移架残余支撑力的精准决策提供了新的研究思路。
为实现极薄煤层破碎顶板条件下液压支架带压移架残余支撑力的精准决策，本文提出了一种基于改进蜣螂算法（Improved Dung Beetle Optimizer，IDBO）优化深度混合核极限学习机（Deep Hybrid Kernel Extreme Learning Machine，DHKELM）的液压支架带压移架残余支撑力决策方法。在混合核极限学习机（Hybrid Kernel Extreme Learning Machine，HKELM）基础上引入极限学习机自动编码器（Extreme Learning Machine Autoencoder，ELM−AE）结构来构建DHKELM模型；引入无限折叠迭代（lterative Chaotic Map with Infinite Collapses，ICMIC）混沌映射、Lévy飞行和贪婪策略对蜣螂算法（Dung Beetle Optimizer，DBO）进行改进，形成IDBO算法；采用IDBO算法对DHKELM的超参数进行优化，构建基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策方法，可实现极薄煤层破碎顶板条件下液压支架带压移架残余支撑力的精准决策，为液压支架自适应调控提供技术支持。
1. IDBO−DHKELM模型
1.1 DHKELM模型
HKELM通过结合径向基函数（Radial Basis Function，RBF）核函数的强学习能力和Poly核函数的优异泛化能力，以权重系数组合构成混合核函数，有效克服了极限学习机（Extreme Learning Machine，ELM）因随机生成隐藏层权值向量和偏置引起的共线性问题[19-20]，显著提升了模型在处理复杂非线性数据时的决策性能。
RBF核函数表达式为
$$ {K_{{\text{RBF}}}}\left( {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'_n}}} \right) = \exp \left( { - \frac{{{{\left\| {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'_n}}} \right\|}^2}}}{{2{\alpha ^2}}}} \right) $$ (1) 式中：${{\boldsymbol{x}}_n}$为第n（n=1，2，$\cdots $，g，g为输入样本向量数量）个输入样本向量；${{\boldsymbol{x}}'_n}$为与${{\boldsymbol{x}}_n}$进行RBF核函数计算的样本向量，${{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'_n}} \in {\boldsymbol{X}}$，${\boldsymbol{X}}$为输入样本矩阵；$\alpha $为RBF核函数参数。
Poly核函数表达式为
$$ {K_{{\text{Poly}}}}\left( {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'_n}}} \right) = {\left[ {\left( {{{\boldsymbol{x}}_n} {{{\boldsymbol{x}}'_n}}} \right) + m} \right]^s} $$ (2) 式中$m$，$s$为Poly核函数参数。
混合核函数表达式为
$$ K\left( {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'}_n}} \right) = r{K_{{\text{RBF}}}}\left( {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'}_n}} \right) + \left( {1 - r} \right){K_{{\text{Poly}}}}\left( {{{\boldsymbol{x}}_n},{{{\boldsymbol{x}}'}_n}} \right) $$ (3) 式中$r$为核权重系数，$r \in \left[ {0,1} \right]$。
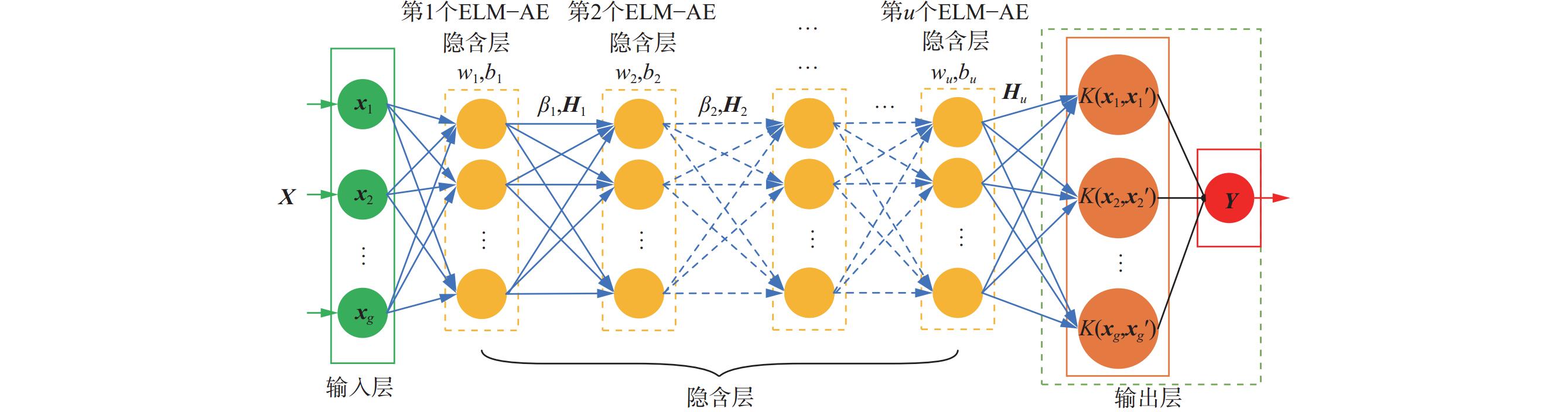
液压支架带压移架残余支撑力受到顶板条件和供液能力等影响，呈现出复杂非线性及动态变化特性。虽然HKELM具备较强的非线性数据拟合能力，但在处理复杂动态特征时，受限于特征提取能力，难以充分挖掘深层次数据特征，从而限制了其在残余支撑力决策中的应用效果。为提升模型对复杂非线性动态特征的提取能力，在HKELM基础上引入ELM−AE结构[21]，形成DHKELM模型，其结构如图1所示。ELM−AE采用无监督学习方式从数据中自动提取深层次特征，提升了DHKELM模型的特征表达能力，从而增强了对残余支撑力复杂变化规律的适应性。
DHKELM具体实现步骤如下：
1） 随机初始化第$i$（$i$=1，2，$\cdots $，$u$，$u$为ELM−AE数量）个ELM−AE隐含层中的输入权重${w_i}$和偏置${b_i}$。
2） 通过将上一个ELM−AE隐含层的输出特征矩阵作为下一个ELM−AE隐含层的输入，依次计算第$i$个ELM−AE隐含层的输出特征矩阵${{\boldsymbol{H}}_i}$和输出权重${\beta _i}$。
$$ {{\boldsymbol{H}}_i} = f\left( {{w_i}{\boldsymbol{X}} + {b_i}} \right) $$ (4) $$ {\beta _i} = {\left( {\frac{{\boldsymbol{I}}}{\delta } + {\boldsymbol{H}}_i^{\mathrm{T}}{{\boldsymbol{H}}_{i - 1}}} \right)^{ - 1}}{\boldsymbol{H}}_i^{\mathrm{T}}{{\boldsymbol{H}}_{i - 1}} $$ (5) 式中：$f\left( \cdot \right)$为激活函数；${\boldsymbol{I}}$为单位矩阵；$\delta $为正则化系数。
3） 将最后一个ELM−AE隐含层的输出特征矩阵${{\boldsymbol{H}}_u}$作为HKELM的决策输入，并计算HKELM的输出权重$\beta $：
$$ \beta = {\left( {\frac{{\boldsymbol{I}}}{\delta } + {\boldsymbol{G}}} \right)^{ - 1}}{{\boldsymbol{H}}_u} $$ (6) 式中${\boldsymbol{G}}$为混合核函数矩阵。
DHKELM的决策值为
$$ {\boldsymbol{Y}} = \left[ \begin{gathered} K\left( {{{\boldsymbol{x}}_1},{{{\boldsymbol{x}}'}_1}} \right) \\ K\left( {{{\boldsymbol{x}}_2},{{{\boldsymbol{x}}'}_2}} \right) \\ \vdots \\ K\left( {{{\boldsymbol{x}}_g},{{{\boldsymbol{x}}'}_g}} \right) \end{gathered} \right]{\left( {\frac{{\boldsymbol{I}}}{\delta } + {\boldsymbol{G}}} \right)^{ - 1}}{\boldsymbol{T}} $$ (7) 式中${\boldsymbol{T}}$为目标输出矩阵。
1.2 IDBO
DBO是一种模拟蜣螂滚球、觅食、繁殖和偷窃行为的群智能优化算法[22]。相比其他群智能算法，DBO算法在处理复杂、多维的优化问题时可表现出较好的收敛性和寻优能力。然而，DBO算法随机初始化种群位置会导致种群分布不均，遍历性较差，从而影响整体求解性能。在算法后期，DBO的收敛速度较慢，特别是在处理具有多个局部最优解的问题时，容易陷入局部最优，影响其全局搜索能力。通过引入ICMIC混沌映射、Lévy飞行与贪婪策略对DBO进行改进，以提高其在DHKELM模型超参数优化时的收敛速度和寻优性能。
1） ICMIC混沌映射。为改善种群的初始分布，引入了ICMIC混沌映射。ICMIC混沌映射具有较好的随机性、均匀性、遍历性，能够有效覆盖搜索空间，减少初始种群分布不均带来的问题，使得初始种群能够更均匀地覆盖搜索空间。ICMIC混沌映射的表达式为
$$ {q_{j + 1}} = \sin \left( {{\rho }/{{{q_j}}}} \right) $$ (8) 式中：${q_j}$为ICMIC映射的第$j$（$j = 1,2,\cdots,{\textit{z}},$${\textit{z}}$为蜣螂数量）个蜣螂位置，$ - 1 \leqslant {q_j} \leqslant + 1$且${q_j} \ne 0$；$\rho $为映射参数，$\rho \in \left( {0, + \infty } \right)$。
2） Lévy飞行和贪婪策略。在个体位置更新过程中，Lévy飞行策略通过引入长跳跃机制，使得算法在搜索过程中能够更有效地跳出局部最优解，增强全局搜索能力。Lévy飞行策略的粒子位置更新表达式为
$$ {q_{\mathrm{a}}} = {q_{\mathrm{b}}} + \left( {{q_{\mathrm{b}}} - {q_{\mathrm{c}}}} \right) C {L_{{\text{Lévy}}}}\left( \lambda \right) $$ (9) 式中：${q_{\mathrm{a}}}$为Lévy飞行策略更新后的粒子位置；${q_{\mathrm{b}}}$为全局最佳粒子位置；${q_{\mathrm{c}}}$为当前粒子位置；$C$为常数，用于调整步长；$ {L_{{\text{Lévy}}}}\left( \cdot \right) $为Lévy飞行路径，遵循Lévy分布；$\lambda $为Lévy飞行步长。
在Lévy飞行的基础上，贪婪策略则进一步保证局部搜索效率。若当前最佳粒子位置${q_{\mathrm{d}}}$的适应度值$F\left( {{q_{\mathrm{d}}}} \right)$大于Lévy飞行策略更新后的粒子位置${q_{\mathrm{a}}}$的适应度值$F\left( {{q_{\mathrm{a}}}} \right)$，则${q_{\mathrm{d}}} = {q_{\mathrm{a}}}$。通过在每次更新时选择最优解的方式，确保每次更新都朝着更优的方向进行。Lévy飞行和贪婪策略的结合不仅加快了收敛速度，还提升了算法的寻优精度。
1.3 IDBO−DHKELM模型
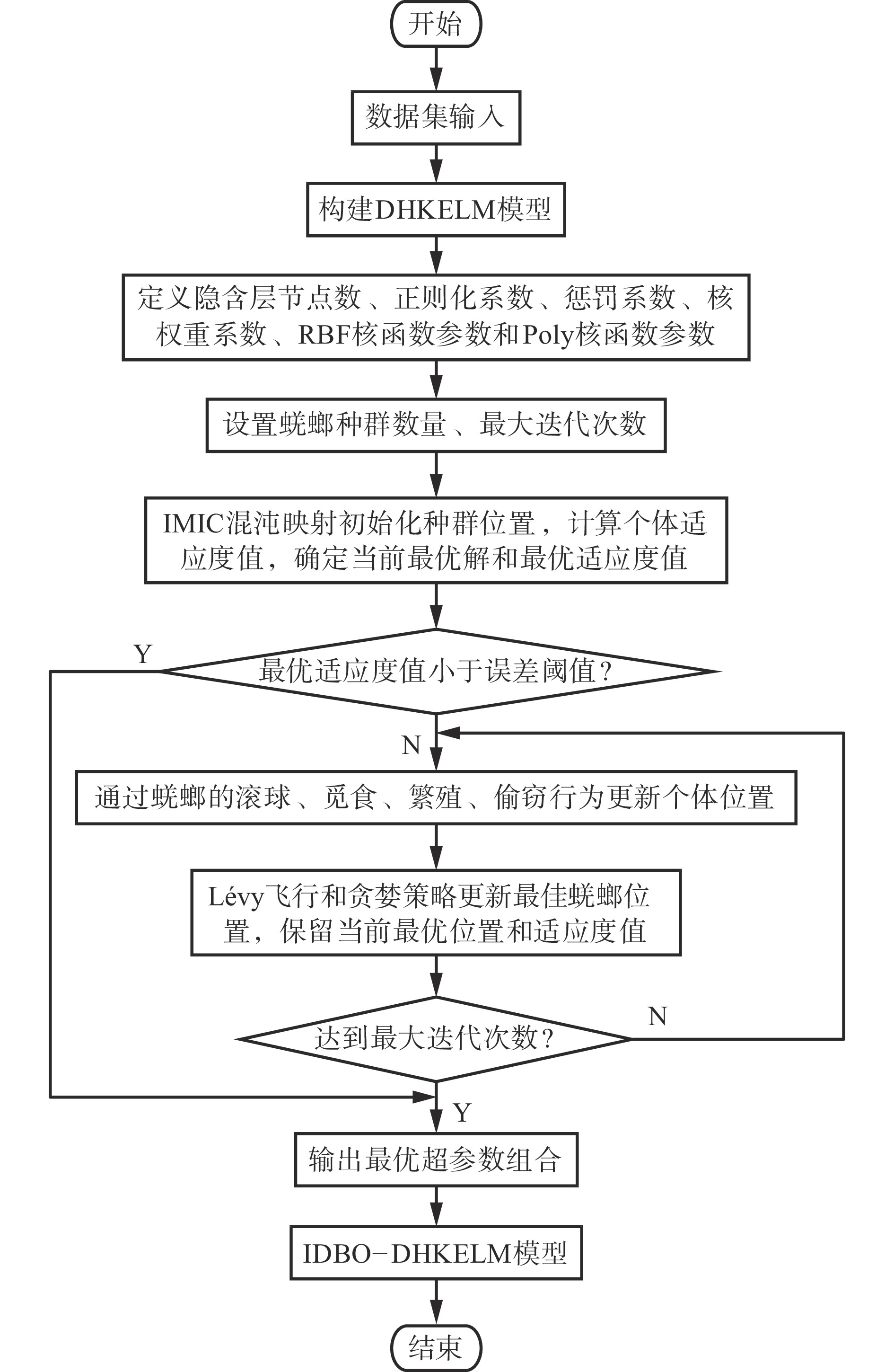
DHKELM模型结合ELM−AE的深层特征提取能力与HKELM的非线性映射能力，在液压支架带压移架残余支撑力决策时，模型的决策性能高度依赖于超参数（隐含层节点数、正则化系数、惩罚系数、核权重系数、RBF核函数参数和Poly核函数参数）的选择。而传统超参数调整方法难以有效获得最优解，且易陷入局部最优。为优化DHKELM的超参数，引入IDBO算法。IDBO通过ICMIC混沌映射生成多样化的初始种群位置，利用Lévy飞行策略增强全局搜索能力，并通过贪婪策略快速收敛到最优解。在复杂参数空间中，IDBO能够自适应搜索超参数组合，显著提升DHKELM的泛化能力与决策精度。IDBO−DHKELM模型建立流程如图2所示。
IDBO−DHKELM模型建立具体步骤如下：
1） 参数初始化。定义隐含层节点数、正则化系数、惩罚系数、核权重系数、RBF核函数参数和Poly核函数参数的寻优范围，并设置蜣螂种群数量和最大迭代次数。
2） 个体位置更新。利用ICMIC混沌映射生成多样化的初始种群位置，并计算个体适应度值，确定当前最优解。检查当前最优适应度值是否小于预设误差阈值：若是，提前终止优化，输出最优参数组合；否则，通过蜣螂的滚球、觅食、繁殖和偷窃行为更新个体位置。同时采用Lévy飞行策略增强全局搜索能力，避免陷入局部最优。每次更新后，通过贪婪策略选择最优解并保留当前最优位置和适应度值。
3） 输出最优解。在满足误差阈值或达到最大迭代次数后，输出最优参数组合。使用优化后的超参数初始化DHKELM模型，建立IDBO−DHKELM模型。
2. 基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策方法
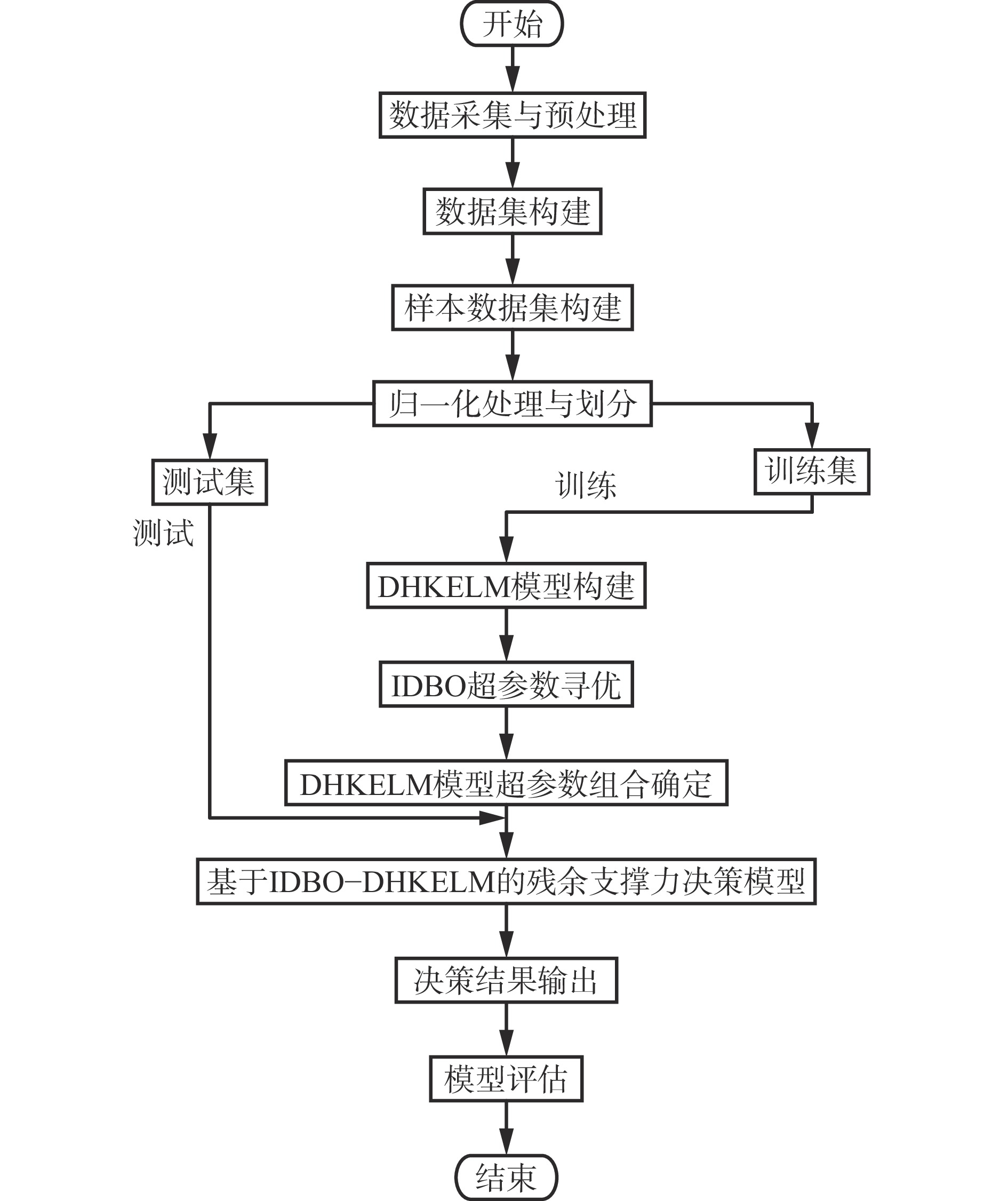
为实现极薄煤层破碎顶板条件下液压支架带压移架时残余支撑力精准决策，利用IDBO优化DHKELM模型的超参数，实现基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策，流程如图3所示。
![]()
图 3 基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策流程Figure 3. Decision-making process of residual support force of hydraulic supports during pressurized moving based on IDBO-DHKELM model基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策具体步骤如下：
1） 数据采集与预处理。通过液压支架电液控制系统的传感器网络，采集液压支架带压移架过程中的立柱压力、推移油缸压力和行程等数据。为应对井下复杂环境导致的数据缺失和异常，采用线性插值法填充缺失数据，并使用时域相邻值替换法修正异常波动数据，确保数据的完整性和准确性。
2） 数据集构建与划分。通过对不同支架支撑力变化特点和带压移架过程中传感器数据进行可视化分析和相关性分析，确定影响带压移架残余支撑力的关键特征，并构建决策样本数据集。为消除不同量纲和数量级差异对模型训练效果的影响，采用min−max归一化方法对样本数据统一缩放至[0，1]范围内。最后将归一化数据按8∶2的比例随机划分为训练集和测试集。
3） 模型训练与决策。将归一化后的训练集数据输入DHKELM模型进行训练，采用均方误差（Mean-Square Error，MSE）作为适应度函数。利用IDBO的自适应性寻优能力优化DHKELM模型超参数。模型训练完成后，将测试集输入IDBO−DHKELM模型进行决策，决策结果反归一化后输出残余支撑力决策值。
3. 实验验证
3.1 实验数据
实验数据来源于延安市禾草沟二号煤矿1123极薄煤层综采工作面。该矿煤层平均厚度为0.79 m，工作面长度为120 m，且工作面倾角近水平。工作面配备80台ZZ4000/6.5/13D中间液压支架和4台ZZG4000/08/16D过渡液压支架。顶板的基本顶主要为泥质粉砂岩和粉砂岩，属中等易破碎顶板；直接顶主要为泥岩和砂质泥岩，其特点为不稳定且易破碎。因此，液压支架在进行跟机移架时，需采用带压移架方式，以确保支架对破碎顶板的有效支护。
在该极薄煤层综采工作面，液压支架电液控制系统通过安装在支架关键部位的传感器，实时监测支架支护状态、运行状态及其他生产数据。通过安装在立柱底腔处的压力传感器监测支架在升/降柱过程中的支撑力。液压支架带压移架时，推移油缸有杆腔进液，无杆腔回液。安装于推移油缸处的行程传感器用于监测推移油缸行程变化，安装于推移油缸有杆腔供液管路上的压力传感器用于监测拉架过程中的推移油缸进液口压力。各传感器每1 s记录1次数据，共采集工作面46 d数据，并通过工业环网传输并储存至地面数据库。
由于井下环境复杂多变，各传感器在数据采集过程中易受到多种因素干扰，导致部分数据出现缺失或异常现象。为保证数据的准确性和完整性，对于数据异常问题，分情况进行处理：单个异常值采用时域相邻值替换，如某一时刻的数据发生异常，则用前一时刻或后一时刻的数值进行替换；若异常数据较多，则去除本台液压支架当天数据。对于缺失数据，采用线性插值法进行填充，通过连接相邻已知的数据点的直线来估算缺失值。
3.2 模型输入变量与数据集划分
在工作面推进过程中，由于顶板上覆岩层应力和垮落步距的变化，导致工作面不同区域的顶板破碎程度和压力产生显著差异，这些差异直接反映在液压支架的支撑力变化上，使得不同区域支架的支撑力变化模式也呈现出不同的特点。本文对2号过渡液压支架和40号中部液压支架的部分支撑力数据变化进行分析，如图4所示。可看出2号过渡液压支架带压移架前支架支撑力变化范围为17.5～34 MPa，带压移架前支架平均支撑力为26.54 MPa；带压移架时残余支撑力变化范围为1～2.5 MPa，平均残余支撑力为1.36 MPa。而40号中部液压支架带压移架前支架支撑力变化范围为25.8～40 MPa，带压移架前支架平均支撑力为33.15 MPa；带压移架时残余支撑力变化范围为1～4 MPa，平均残余支撑力为2.31 MPa。对比分析表明，中部液压支架区域的顶板压力较高且破碎程度较大，支架需要更高的支撑力以维持顶板的稳定性，因此残余支撑力相对更高。而过渡液压支架区域顶板压力相对较低、破碎程度较小，带压移架前支架支撑力和带压移架时残余支撑力均较低且变化幅度较小。这表明，不同区域支架的带压移架前支撑力在一定程度上决定了带压移架时残余支撑力，反映了顶板破碎程度对液压支架支护性能的显著影响。
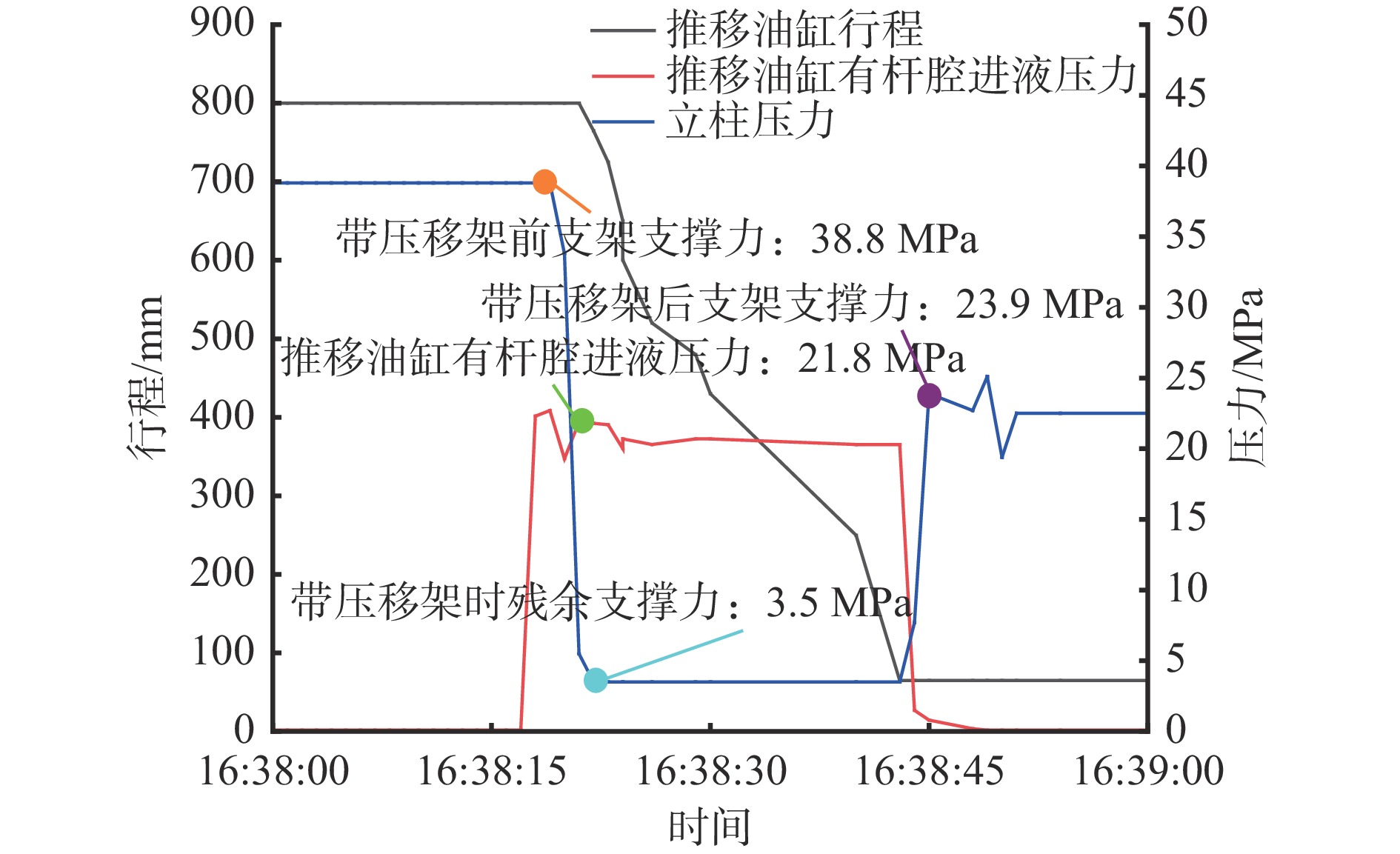
对第50号液压支架在带压移架工况下的支架支撑力、推移油缸进液压力及推移油缸行程的变化进行可视化，如图5所示。当支架进行带压移架时，操作人员同时打开降柱和移架手柄。移架手柄被打开后，供液系统向推移油缸有杆腔供液，从而使支架产生一定的拉架力，但由于带压移架前支架支撑力较高，导致拉架阻力过大，推移油缸行程并未发生变化。为顺利完成带压移架，必须降低支架支撑力以减小拉架阻力。当推移油缸进液压力为21.8 MPa时，支架支撑力从初始的38.8 MPa开始逐渐下降，当支架支撑力下降至3.5 MPa时，推移油缸行程开始减小，此时操作人员停止降柱操作。推移油缸行程继续减小，直至减少至65 mm，达到所需移架位移后，停止移架操作。最后，支架支撑力由3.5 MPa上升至23.9 MPa，完成升柱动作。这一过程表明，推移油缸的有杆腔进液压力和推移油缸行程变化速度（液压支架带压移架过程中，推移油缸行程随时间变化的速率）直接影响残余支撑力的调控。
![]()
图 5 50号液压支架带压移架时数据变化曲线Figure 5. Data variation curves of No.50 hydraulic support during pressurized moving通过对不同位置支架支撑力变化和带压移架过程的可视化分析，结合现场调研和工人操作经验，得出不同支架的带压移架前支架支撑力、推移油缸进液压力、推移油缸行程变化速度和工作面倾角是影响带压移架残余支撑力的关键因素。为进一步量化这些因素的影响，采用皮尔逊相关系数对各影响因素与残余支撑力进行相关性分析，见表1（为便于比较，所有相关系数取绝对值，值越大，表明相关性越强）。结果表明，推移油缸进液压力、带压移架前支架支撑力、推移油缸行程变化速度、支架号和工作面倾角与残余支撑力的相关性依次减弱。由于该极薄煤层工作面倾角接近水平，所以工作面倾角与残余支撑力相关性较低，可忽略其影响。确定带压移架前支架支撑力、推移油缸进液压力、推移油缸行程变化速度和支架号是影响残余支撑力的关键特征并作为IDBO−DHKELM模型的输入变量，残余支撑力为模型的输出变量。经过数据筛选，共构建5 142组样本数据，其中包含4 836组中部液压支架样本和306组过渡液压支架样本。最后，将样本数据进行归一化处理，并按照8∶2的比例随机划分为训练集和测试集，分别用于模型的训练和测试。
表 1 残余支撑力与各影响因素相关性分析结果Table 1. Correlation analysis between residual support force and influencing factors参数 皮尔逊相关系数 推移油缸
进液压力带压移架前
支架支撑力推移油缸行程
变化速度支架号 工作面倾角 带压移架
残余支撑力0.41 0.33 0.18 0.15 0.07 3.3 模型决策评估指标
为全面评估模型的决策性能，选取平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Squared Error，RMSE）及决定系数R2作为模型决策评估指标。MAE用于衡量模型决策值与实际值之间的平均绝对差异，MAE越小，表明模型整体决策精度越高；RMSE用于反映模型决策值与实际值之间差异的平方均值，RMSE越小，表明模型的决策误差越小，决策效果越好；R2反映模型对数据的拟合程度，取值范围为[0，1]，R2越接近于1，表明模型对实际数据的拟合程度越强。
3.4 模型决策结果及评价
对比分析ELM，HKELM，DHKELM，IDBO−DHKELM模型在残余支撑力决策中的表现；通过使用Schwefel函数和Rastrigin函数对PSO，DBO，IDBO算法进行对比测试，验证IDBO算法在参数优化方面的优势，并分析不同优化算法对DHKELM模型超参数优化效果的影响。
3.4.1 模型决策结果对比分析
ELM，HKELM，DHKELM和IDBO−DHKELM模型的决策结果对比如图6所示。ELM模型的残余支撑力决策值与实际值之间存在较大的偏差，表现出较差的决策效果，这是由于ELM模型单一隐含层结构和随机的权值和偏置在处理复杂的非线性数据时，难以有效学习和表达数据中的复杂模式。HKELM模型通过引入混合核技术，改善了模型处理复杂非线性数据的能力，HKELM模型的残余支撑力决策值与实际值的偏差较ELM模型有所减小。DHKELM模型通过结合ELM−AE结构和混合核技术优势，有效提升了数据的特征表达和非线性映射能力，其决策值相比于ELM和HKELM模型更接近实际值，但仍存在一定的误差。IDBO−DHKELM模型通过引入IDBO算法，自适应调整超参数，优化DHKELM模型的训练过程，增强了模型对复杂非线性数据动态变化特征的学习能力，显著降低了决策误差，使得模型决策值更加接近实际值。由此可见，IDBO−DHKELM模型在残余支撑力决策方面表现出了最佳效果。
不同模型的决策结果评价见表2。IDBO−DHKELM模型在各项评价指标上均优于ELM，HKELM和DHKELM模型。其RMSE为0.143，较ELM，HKELM和DHKELM模型分别降低了61.89%，53.87%和43.07%；MAE为0.119，较ELM，HKELM和DHKELM模型分别降低了61.84%，53.03%和42.53%，表明IDBO−DHKELM模型在残余支撑力决策精度上具有显著的优势；R2为0.971，较ELM，HKELM和DHKELM模型分别提升了23.24%，12.38%和6.35%，表明IDBO−DHKELM模型对残余支撑力的拟合效果较好。
3.4.2 DHKELM模型参数优化方法决策分析
为验证IDBO在收敛速度和寻优精度上的优势，选择CEC2005基准函数集中的Schwefel函数测试IDBO全局寻优能力，以及Rastrigin函数测试其在处理多个局部最优解时的局部搜索性能。测试函数的维度、取值范围和最优解信息见表3。
表 2 不同模型的决策结果评价Table 2. Evaluation of different models in decision-making模型 RMSE MAE R2 ELM 0.376 0.312 0.788 HKELM 0.310 0.253 0.864 DHKELM 0.251 0.207 0.913 IDBO−DHKELM 0.143 0.119 0.971 表 3 测试函数Table 3. Test functions函数 维度 取值范围 最优解 Schwefel 30 [−100，100] 0 Rastrigin 30 [−5.12，5.12] 0 在Schwefel和Rastrigin函数测试过程中，将IDBO与PSO，DBO算法进行对比分析，为减少随机因素的影响，并保证实验的公平性，种群规模和最大迭代次数统一设置为30和300，每个测试函数独立运行10次，绘制平均适应度值变化曲线，如图7所示。可看出在Schwefel函数测试过程中，3种算法的适应度值均随着迭代次数的增加逐渐收敛，其中IDBO算法的收敛速度最快，DBO算法次之，且均达到最优适应度值0，PSO算法的收敛速度较慢，未达到最优适应度值。在Rastrigin函数测试中，PSO算法未达到收敛状态，IDBO算法收敛速度仍最佳。由此可见，IDBO算法在收敛速度和寻优精度上均优于DBO和PSO算法，证明了其高效性、稳定性。
在此基础上，分析不同优化算法（PSO，DBO和IDBO）对DHKELM模型超参数优化的决策效果。实验参数设置：种群数量为30，最大迭代次数为50。DHKELM模型的隐含层节点数、核权重系数、惩罚系数、正则化系数、RBF核函数参数$\alpha $、Poly核函数参数$m$和$s$寻优范围分别设定为[1，100]，[0，1]，[10−3，103]，[10−3，103]，[10−2，102]，[10−2，102]和[1，10]。
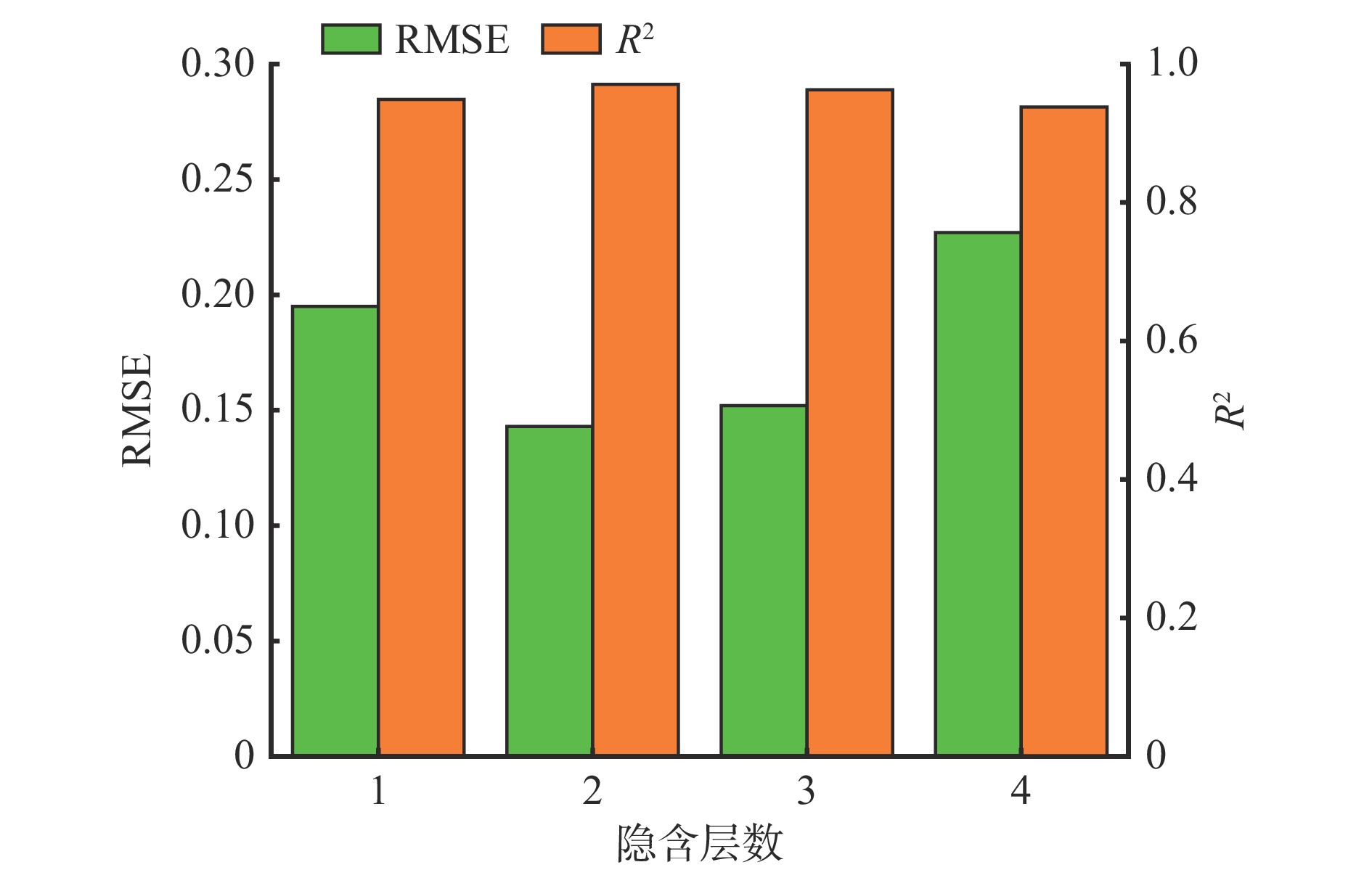
为探讨不同隐含层数对DHKELM模型决策效果的影响，分析不同隐含层数下模型的R2和RMSE，如图8所示。当隐含层数为2时，R2最大（0.971）、RMSE最小（0.143），决策准确率最佳。随着隐含层数增加，决策准确率降低，当隐含层数为4时，R2最小（0.938）、RMSE最大（0.227），决策准确率最差。因此，设置DHKELM模型的隐含层数为2。
![]()
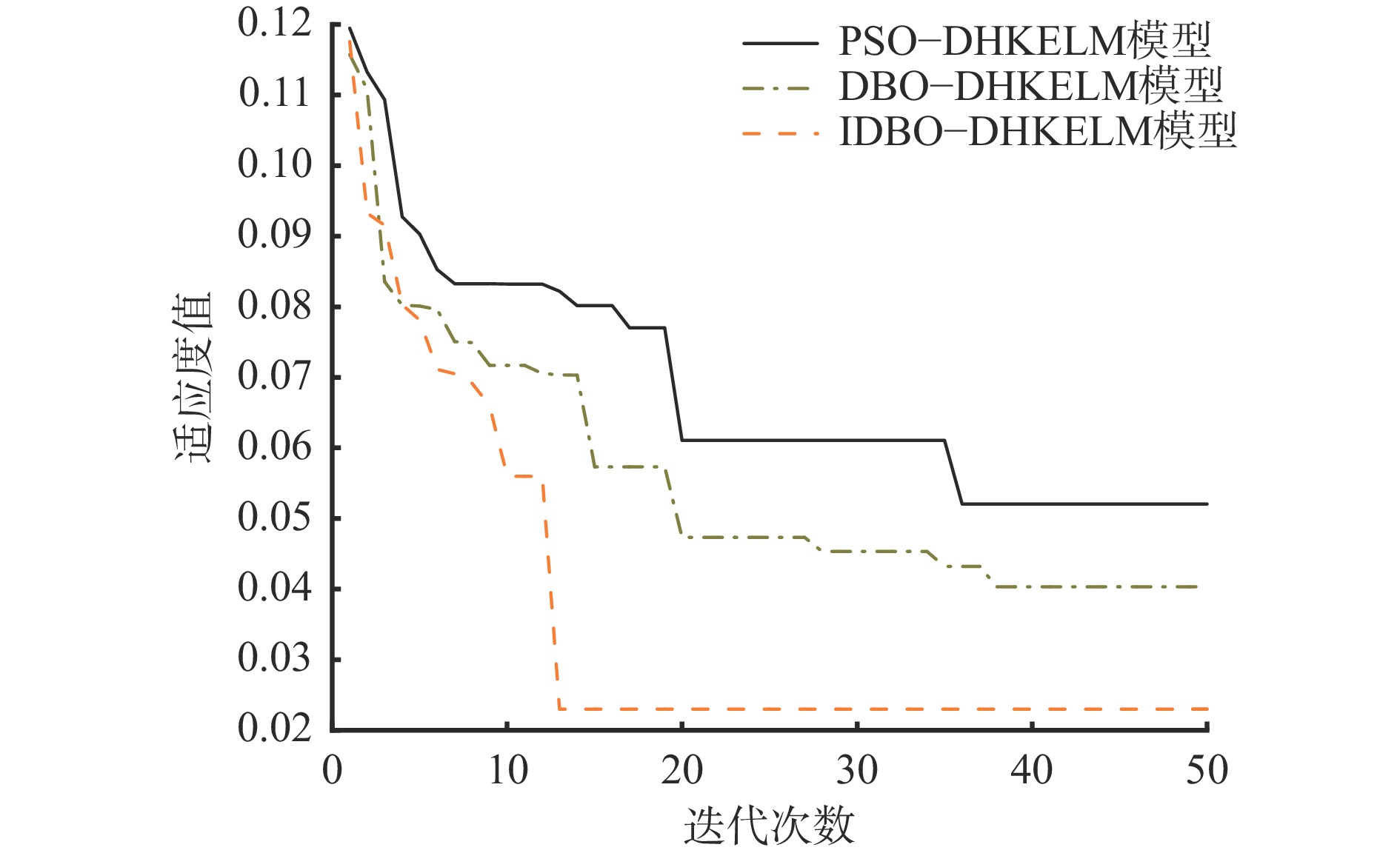
图 8 不同隐含层数下的决策结果Figure 8. Decision-making results under different hidden layers configurations不同算法优化DHKELM模型的适应度值随迭代次数变化曲线如图9所示。可看出不同算法优化DHKELM模型的适应度值随着迭代次数增加逐渐减小，其中IDBO−DHKELM模型表现出较快的收敛速度和较小的误差，在迭代到第13次时，适应度值达到最小（0.023）且趋于稳定状态，表明IDBO优化DHKELM模型超参数时具有较好的收敛性和寻优精度。IDBO优化的最优超参数组合：第1层隐含层节点数为30，第2层隐含层节点数为58，核权重系数为0.36，惩罚系数为142.64，正则化系数为353.57，RBF核函数参数$\alpha $为69.53，Ploy核函数参数$m$，$s$分别为41.16，6。
![]()
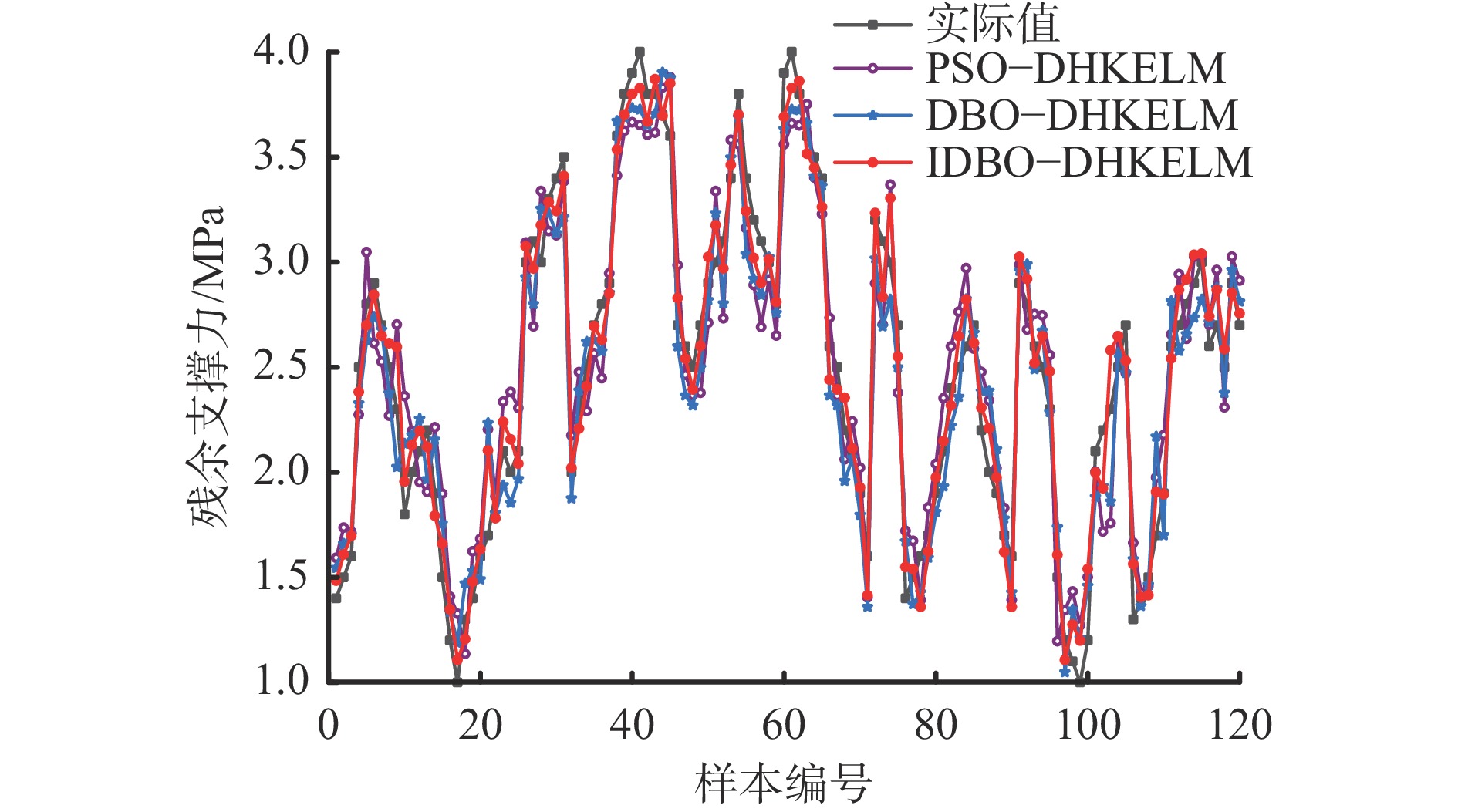
图 9 不同算法优化DHKELM模型迭代曲线Figure 9. Iteration curves of different algorithms for optimizing DHKELM model不同算法优化DHKELM模型的决策结果如图10所示。可看出相较于基于DBO−DHKELM和PSO−DHKELM模型，基于IDBO−DHKELM模型的残余支撑力决策值更接近实际值。
![]()
图 10 不同算法优化DHKELM模型决策结果对比Figure 10. Comparison of decision-making performance among different algorithms optimizing DHKELM model采用评价指标定量分析PSO−DHKELM，DBO−DHKELM和IDBO−DHKELM模型的决策结果，见表4。可看出相较于PSO−DHKELM，DBO−DHKELM模型，IDBO−DHKELM模型RMSE分别降低了40.90%，35%，MAE分别降低了41.38%，32.39%，R2分别提升了4.97%，2.97%。表明利用IDBO优化DHKELM模型超参数，可有效提高残余支撑力决策精度。
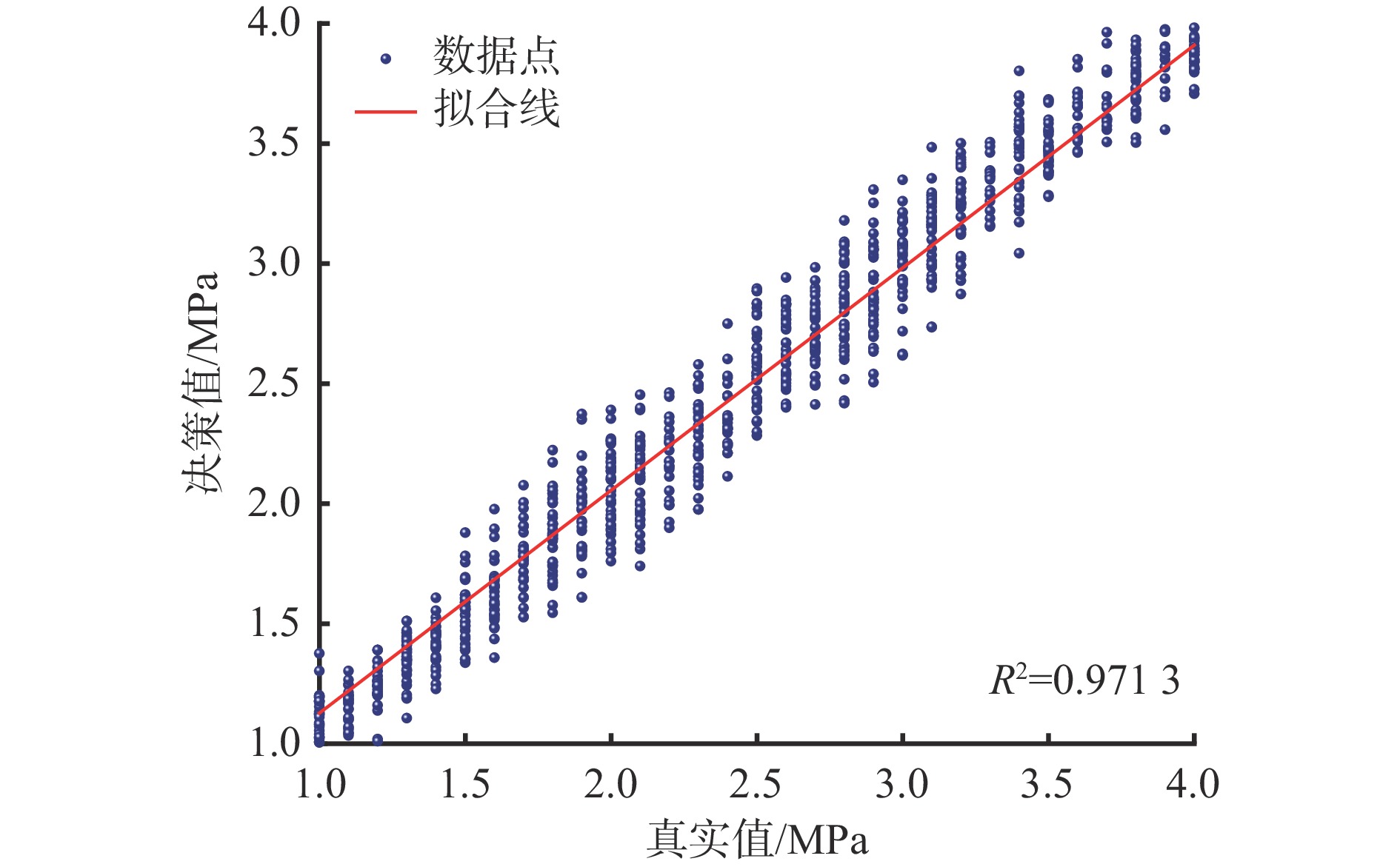
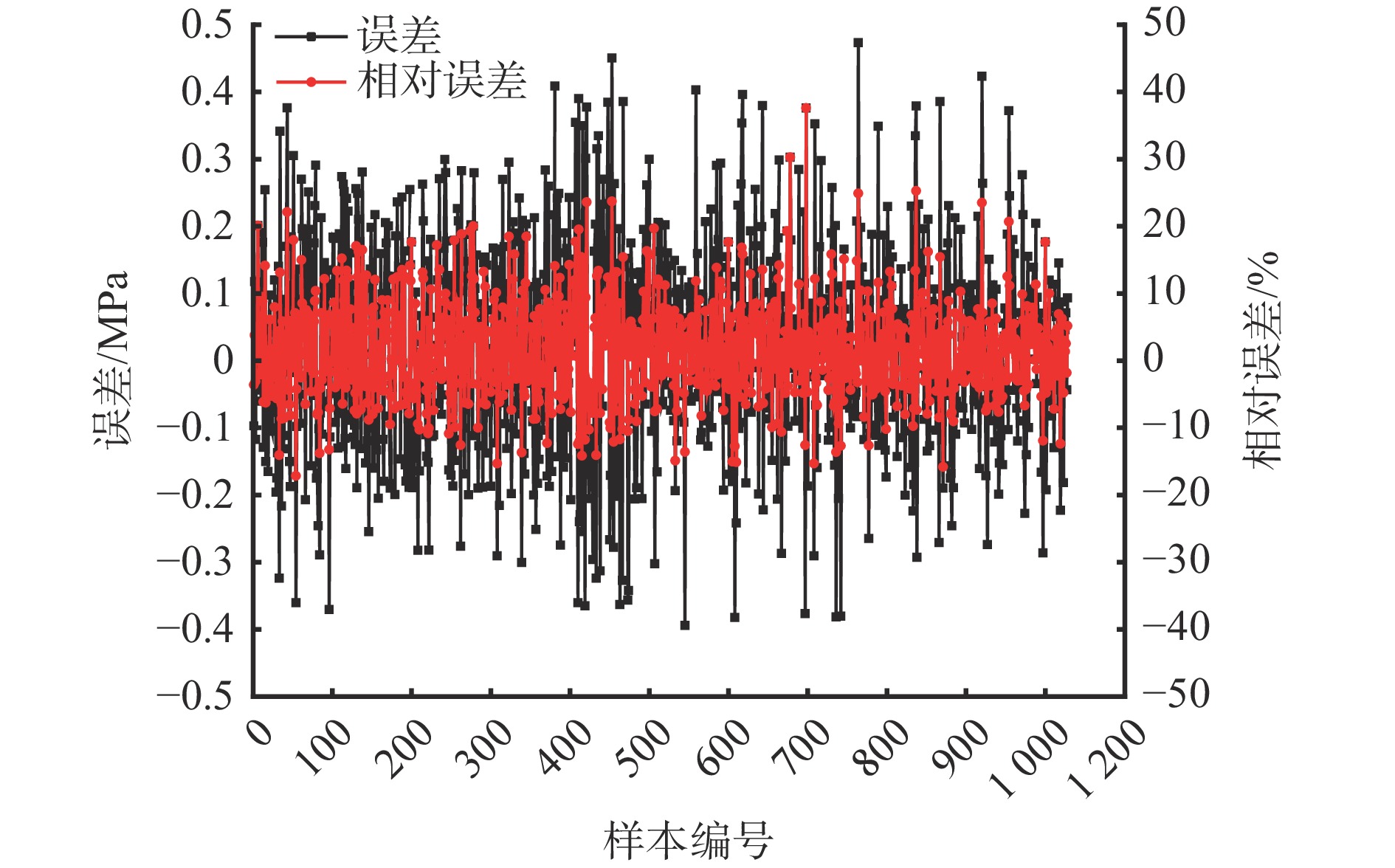
表 4 不同算法优化DHKELM模型决策结果评价Table 4. Evaluation of different optimization algorithms for DHKELM model模型 RMSE MAE R2 PSO−DHKELM 0.242 0.203 0.925 DBO−DHKELM 0.220 0.176 0.943 IDBO−DHKELM 0.143 0.119 0.971 此外，利用Matlab中内置的图像生成函数，绘制IDBO−DHKELM模型的决策结果和误差，分别如图11、图12所示。可看出数据点紧密地集中在拟合线附近，表明IDBO−DHKELM模型在对残余支撑力决策时具有较好的拟合效果；IDBO−DHKELM模型的决策值与实际值的误差不超过0.5 MPa，且相对误差集中在10%以内，表明IDBO−DHKELM模型具有较高的决策精度和稳定性。
4. 结论
1） 在HKELM基础上引入ELM−AE结构，构建了DHKELM模型，以增强对复杂输入的特征提取和非线性映射能力。引入ICMIC混沌映射、Lévy飞行和贪婪策略对DBO算法进行改进，形成IDBO算法，该算法具备更高的寻优精度和更快的收敛速度。利用IDBO算法优化DHKELM模型的超参数，构建了基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策方法。
2） 结合极薄煤层综采工作面液压支架带压移架实测数据，采用线性插值和时域相邻值替换法对数据进行预处理。通过可视化和相关性分析，确定支架号、带压移架前支架支撑力、推移油缸进液压力和推移油缸行程变化速度为影响液压支架带压移架残余支撑力的关键特征。
3） 采用Schwefel和Rastrigin函数对IDBO算法进行性能测试，结果表明，IDBO算法在寻优精度和收敛速度上均优于PSO和DBO算法。不同模型决策性能对比结果表明，IDBO−DHKELM模型的残余支撑力决策结果的RMSE，MAE和R²分别为0.143，0.119和0.971，其决策精度显著优于ELM，HKELM和DHKELM模型。
-
![]()
图 3 基于IDBO−DHKELM模型的液压支架带压移架残余支撑力决策流程
Figure 3. Decision-making process of residual support force of hydraulic supports during pressurized moving based on IDBO-DHKELM model
![]()
图 5 50号液压支架带压移架时数据变化曲线
Figure 5. Data variation curves of No.50 hydraulic support during pressurized moving
![]()
图 8 不同隐含层数下的决策结果
Figure 8. Decision-making results under different hidden layers configurations
![]()
图 9 不同算法优化DHKELM模型迭代曲线
Figure 9. Iteration curves of different algorithms for optimizing DHKELM model
![]()
图 10 不同算法优化DHKELM模型决策结果对比
Figure 10. Comparison of decision-making performance among different algorithms optimizing DHKELM model
表 1 残余支撑力与各影响因素相关性分析结果
Table 1 Correlation analysis between residual support force and influencing factors
参数 皮尔逊相关系数 推移油缸
进液压力带压移架前
支架支撑力推移油缸行程
变化速度支架号 工作面倾角 带压移架
残余支撑力0.41 0.33 0.18 0.15 0.07 
下载: 导出CSV
表 2 不同模型的决策结果评价
Table 2 Evaluation of different models in decision-making
模型 RMSE MAE R2 ELM 0.376 0.312 0.788 HKELM 0.310 0.253 0.864 DHKELM 0.251 0.207 0.913 IDBO−DHKELM 0.143 0.119 0.971
下载: 导出CSV
表 3 测试函数
Table 3 Test functions
函数 维度 取值范围 最优解 Schwefel 30 [−100，100] 0 Rastrigin 30 [−5.12，5.12] 0
下载: 导出CSV
表 4 不同算法优化DHKELM模型决策结果评价
Table 4 Evaluation of different optimization algorithms for DHKELM model
模型 RMSE MAE R2 PSO−DHKELM 0.242 0.203 0.925 DBO−DHKELM 0.220 0.176 0.943 IDBO−DHKELM 0.143 0.119 0.971
下载: 导出CSV
-
[1] 袁永,屠世浩,陈忠顺,等. 薄煤层智能开采技术研究现状与进展[J]. 煤炭科学技术,2020,48(5):1-17. YUAN Yong,TU Shihao,CHEN Zhongshun,et al. Current situation and development of intelligent mining technology for thin coal seams[J]. Coal Science and Technology,2020,48(5):1-17.
[2] ZHAO Tongbin,ZHANG Zhenyu,TAN Yunliang,et al. An innovative approach to thin coal seam mining of complex geological conditions by pressure regulation[J]. International Journal of Rock Mechanics and Mining Sciences,2014,71:249-257. DOI: 10.1016/j.ijrmms.2014.05.021
[3] 童应山,王森,张连东,等. 基于覆岩破断特征的极薄煤层工作面支架工作阻力确定[J]. 西安科技大学学报,2024,44(1):64-73. TONG Yingshan,WANG Sen,ZHANG Liandong,et al. Determination of support working resistance in the working face of extremely-thin coal seam based on overburden fracture characteristics[J]. Journal of Xi'an University of Science and Technology,2024,44(1):64-73.
[4] 王国法,刘峰,庞义辉,等. 煤矿智能化——煤炭工业高质量发展的核心技术支撑[J]. 煤炭学报,2019,44(2):349-357. WANG Guofa,LIU Feng,PANG Yihui,et al. Coal mine intellectualization:the core technology of high quality development[J]. Journal of China Coal Society,2019,44(2):349-357.
[5] 周开平. 薄煤层智能化无人工作面成套装备与技术[J]. 煤炭科学技术,2020,48(3):59-67. ZHOU Kaiping. Complete equipment and technology for intelligent unmanned working face in thin coal seam[J]. Coal Science and Technology,2020,48(3):59-67.
[6] 杨生华,周永昌,芮丰,等. 薄煤层开采与成套装备技术的发展趋势[J]. 煤炭科学技术,2020,48(3):49-58. YANG Shenghua,ZHOU Yongchang,RUI Feng,et al. Development trend of thin coal seam mining and complete equipment technology[J]. Coal Science and Technology,2020,48(3):49-58.
[7] 王国法,刘峰,孟祥军,等. 煤矿智能化(初级阶段)研究与实践[J]. 煤炭科学技术,2019,47(8):1-36. WANG Guofa,LIU Feng,MENG Xiangjun,et al. Research and practice on intelligent coal mine construction (primary stage)[J]. Coal Science and Technology,2019,47(8):1-36.
[8] 葛世荣. 智能化采煤装备的关键技术[J]. 煤炭科学技术,2014,42(9):7-11. GE Shirong. Key technology of intelligent coal mining equipment[J]. Coal Science and Technology,2014,42(9):7-11.
[9] 牛剑峰. 综采液压支架跟机自动化智能化控制系统研究[J]. 煤炭科学技术,2015,43(12):85-91. NIU Jianfeng. Study on automatic and intelligent following control system of hydraulic powered support in fully-mechanized coal mining face[J]. Coal Science and Technology,2015,43(12):85-91.
[10] 付翔,李浩杰,张锦涛,等. 综采液压支架中部跟机多模态人机协同控制系统[J]. 煤炭学报,2024,49(3):1717-1730. FU Xiang,LI Haojie,ZHANG Jintao,et al. Multimodal human-machine collaborative control system for hydraulic supports following the shearer in the middle range of fully mechanized mining face[J]. Journal of China Coal Society,2024,49(3):1717-1730.
[11] 朱金雨,李国莲. 液压支架跟机自动化系统设计[J]. 工矿自动化,2013,39(12):1-4. DOI: 10.7526/j.issn.1671-251X.2013.12.001 ZHU Jinyu,LI Guolian. Design of machinery-tracked automatic system of hydraulic support[J]. Industry and Mine Automation,2013,39(12):1-4. DOI: 10.7526/j.issn.1671-251X.2013.12.001
[12] 韩宝珠,安叶青. 基于PLC的液压支架带压移架控制技术[J]. 煤炭技术,2022,41(7):185-187. HAN Baozhu,AN Yeqing. Control technology of hydraulic support moving under pressure based on PLC[J]. Coal Technology,2022,41(7):185-187.
[13] 杨科,池小楼,刘帅. 大倾角煤层综采工作面液压支架失稳机理与控制[J]. 煤炭学报,2018,43(7):1821-1828. YANG Ke,CHI Xiaolou,LIU Shuai. Instability mechanism and control of hydraulic support in fully mechanized longwall mining with large dip[J]. Journal of China Coal Society,2018,43(7):1821-1828.
[14] 张武,贾艳平,路正雄,等. 大采高液压支架带压移架性能研究[J]. 煤矿机械,2020,41(7):53-55. ZHANG Wu,JIA Yanping,LU Zhengxiong,et al. Performance study on moving support with pressure for hydraulic support in large mining height[J]. Coal Mine Machinery,2020,41(7):53-55.
[15] 曹连民,张亚珠,郭徽,等. 大采高液压支架带压移架技术[J]. 煤矿安全,2018,49(3):83-86. CAO Lianmin,ZHANG Yazhu,GUO Hui,et al. Advancing support with pressure technology for hydraulic support with large mining height[J]. Safety in Coal Mines,2018,49(3):83-86.
[16] 李志旭. 液压支架带压移架控制技术研究与应用[D]. 青岛:山东科技大学,2020. LI Zhixu. Research and application on control technology of advancing support with pressure for hydraulic support[D]. Qingdao:Shandong University of Science and Technology,2020.
[17] 曾庆田,吕珍珍,石永奎,等. 基于Prophet+LSTM模型的煤矿井下工作面矿压预测研究[J]. 煤炭科学技术,2021,49(7):16-23. ZENG Qingtian,LYU Zhenzhen,SHI Yongkui,et al. Research on prediction of underground coal mining face pressure based on Prophet+LSTM model[J]. Coal Science and Technology,2021,49(7):16-23.
[18] 王鹏,伍永平,王栓林,等. 矿井瓦斯浓度Lagrange−ARIMA实时预测模型研究[J]. 煤炭科学技术,2019,47(4):141-146. WANG Peng,WU Yongping,WANG Shuanlin,et al. Study on Lagrange-ARIMA real-time prediction model of mine gas concentration[J]. Coal Science and Technology,2019,47(4):141-146.
[19] TIAN Zhongda,LI Shujiang,WANG Yanhong,et al. Wind power prediction method based on hybrid kernel function support vector machine[J]. Wind Engineering,2018,42(3):252-264.
[20] 王超,蔺红,庞晓虹. 基于HPO−VMD和MISMA−DHKELM的短期光伏功率组合预测[J]. 太阳能学报,2023,44(12):65-73. WANG Chao,LIN Hong,PANG Xiaohong. Short-term photovoltaic power combination prediction based on HPO-VMD and MISMA-DHKELM[J]. Acta Energiae Solaris Sinica,2023,44(12):65-73.
[21] CHU Yunfei,FENG Chunyan,GUO Caili,et al. Network embedding based on deep extreme learning machine[J]. International Journal of Machine Learning and Cybernetics,2019,10(10):2709-2724.
[22] XUE Jiankai,SHEN Bo. Dung beetle optimizer:a new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing,2023,79(7):7305-7336.
计量
- 文章访问数: 73
- HTML全文浏览量: 8
- PDF下载量: 12
