0.   引言

智能装备是智慧矿山建设的根本远景，千米钻机作为煤层气开采的核心设备优先向智能化转型，其电控系统要求信号检测精度高、二次系统抗干扰能力强。为进一步提升状态感知能力，研发以精密小信号检测电路和微处理器为核心的电控系统成为趋势^[1-2]。但电控系统一次回路的真空接触器因控制或故障保护功能频繁开合，随着钻进深度增加，开断电流高达4 000 A，期间触头电弧重燃产生瞬态电磁场^[3]，传导进入二次回路将导致小信号检测电路呈现不稳定现象^[4-5]。

千米钻机属于一二设备融合系统，一次侧开关设备操作是导致二次回路故障的主要原因^[6]，二次侧操作瞬态干扰的研究主要集中在干扰信号特征提取和瞬态干扰传播机理。干扰特征提取常用短时傅里叶变换、广义S变换及小波变换^[7-8]，均存在时频聚集性较弱、无法自适应划分频带的不足。为此，文献[9]提出一种改进的经验模态分解（Empirical Mode Decomposition, EMD）方法，能够不依赖人工选择分解基，自适应分解信号。瞬态干扰传播机理通过电流互感器高频建模^[10]、受损元件现场测试^[11]、三维电磁场数字模型^[12-13]等方法，分析干扰的耦合方式、传播路径及空间电磁场分布。

现有受扰机理研究更侧重于一次回路具有直接连接关系的二次侧端口设备，如电压/电流互感器。二次回路，尤其是矿用机电设备电控系统二次回路的稳定性分析与之不同，呈现新的特点。一方面，千米钻机电控系统工况复杂、负载多变，并且融合多个一次回路，各回路交互作用必然改变自身的传导电磁干扰，从而使瞬态干扰频谱分布随机性高，EMD提取此类复杂信号时易出现模态混叠现象^[14]。另一方面，为提升智能感知精度，二次回路中的信号检测回路往往采用高带宽增益运算放大器，其对瞬态干扰下的环路中引脚寄生电容更加敏感^[15]，已有适用于二次侧端口设备的模型不再适用于小信号检测电路的稳定性分析。

此外，千米钻机电控系统瞬态干扰频域分布范围广泛，在抗干扰方面，要求电路在很宽的频域内有较强的抗干扰能力。传统抗干扰措施中，去耦电容存在频带较窄、高频抑制作用不佳的缺陷^[6]，多级RC、LC滤波电路存在阻抗不匹配、体积大的问题^[16]。二次小信号检测电路需根据瞬态干扰特征，进行更加有针对性的抗干扰设计。

为解决千米钻机电控系统瞬态干扰信号分析与抗干扰设计中存在的问题，本文针对15000型千米钻机电控系统的二次回路信号采集电路，采用无参尺度空间表达的经验小波变换（Empirical Wavelet Transform，EWT）算法，提取实测干扰信号频谱中有意义的振荡分量频率分布。通过建立第一级信号采集电路的失效模型，模拟瞬态干扰频域特征对电路稳定性的影响。针对性设计含铁氧体磁珠的二阶滤波电路，并通过实验验证滤波电路的有效性。

1.   瞬态干扰信号分析

1.1   干扰途径分析

千米钻机电控系统融合两回路对钻车电动机和泵车电动机进行控制与保护。瞬态干扰主要由真空接触器等开关器件触头电弧重燃引起^[17]，存在杂散参数产生的高频谐振分量，瞬态电磁场频率、幅值、持续时间等特征量与开关器件型号、电压等级、负载类型等因素相关。IEC 61000−4将开关设备触头电弧重燃产生的干扰定义为持续时间几微秒到几十毫秒的瞬态脉冲群，脉冲群由一组单脉冲组成，单脉冲包含1种或多种高频分量，其频谱分布较为稳定且集中，单个频率波形可由阻尼振荡脉冲函数描述^[18]。

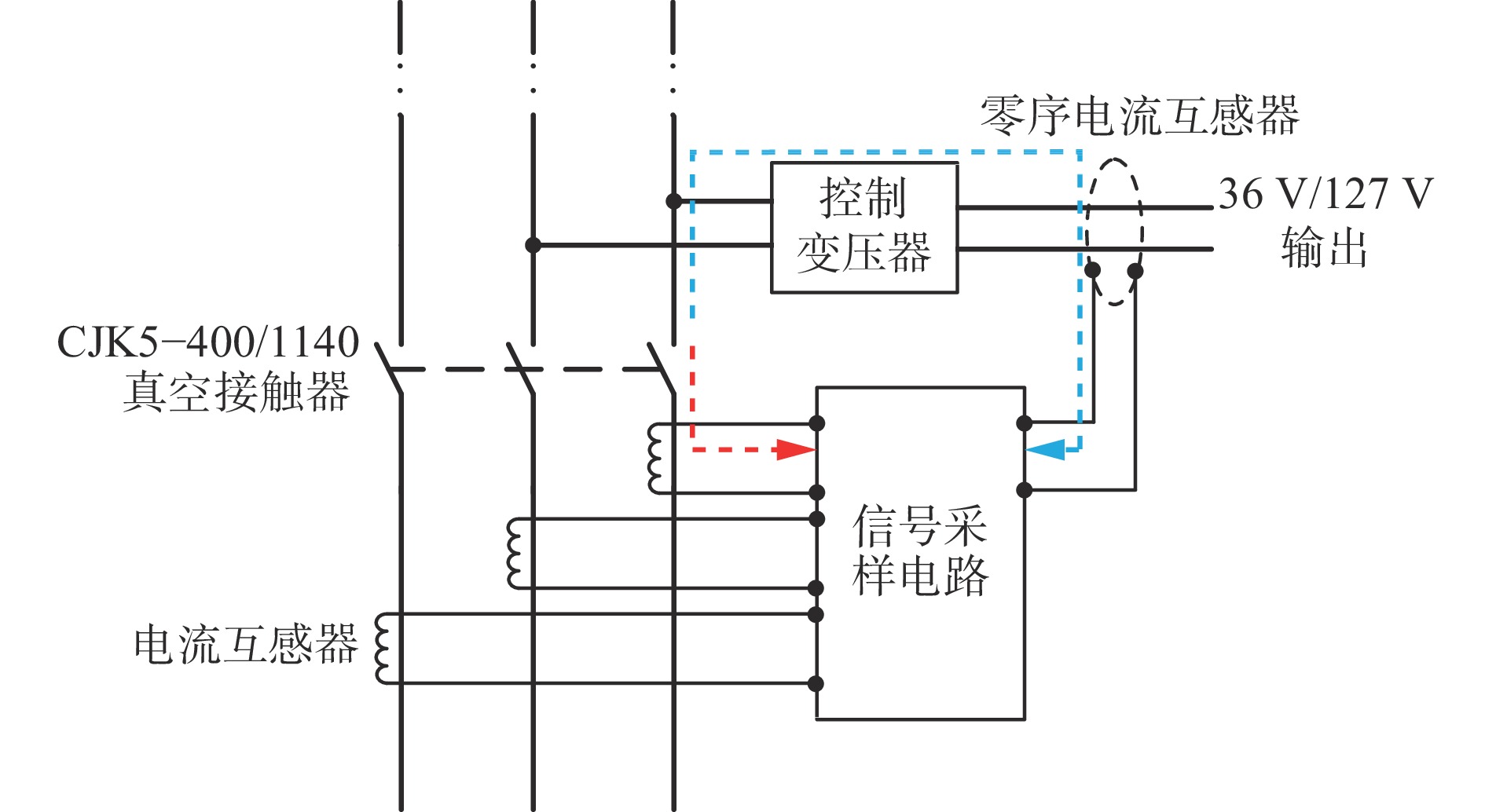
瞬态干扰通过“一次回路真空接触器−电压/电流互感器−小信号电路”及“一次回路真空接触器−控制变压器−电压/电流互感器−小信号电路”的途径进入电控系统二次回路，如三相电流采样电路、零序电流采样电路，如图1所示。

图  1  电控系统本回路典型接线

Figure  1.  Typical wiring of this loop of electronic control system

下载: 全尺寸图片 幻灯片

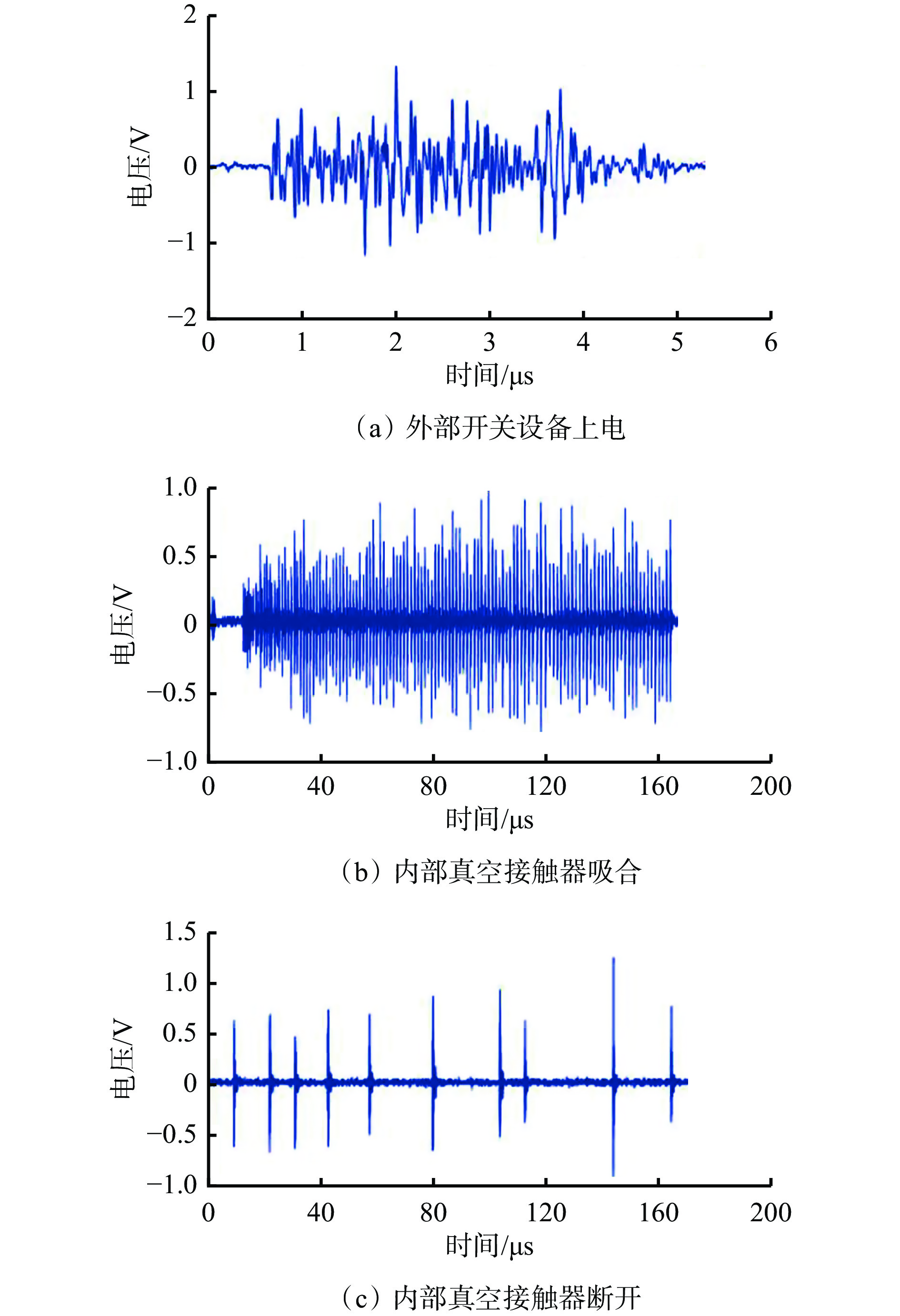
采用高带宽电压探头测量15000型千米水平定向钻机自身及外部其他电控系统的开关器件操作时电磁式互感器二次端口的干扰信号，如图2所示。可看出：当真空接触器吸合、断开时，干扰脉冲群数量存在明显差异，吸合瞬态干扰由上百个单脉冲组成，而断开瞬态干扰分布稀疏，仅由数十个单脉冲组成；外部开关设备上电时瞬态干扰持续时间较短，且无明显脉冲群。

图  2  开关器件操作时互感器二次端口干扰信号

Figure  2.  Interference signal at secondary port of transformer during operation of each switching device

下载: 全尺寸图片 幻灯片

1.2   信号特征提取

无参尺度空间表达的EWT核心是频谱自适应划分，在尺度空间中，随着每层尺度参数的增加，使干扰频谱中大量的“嘈杂”波形与有意义频谱边界的区分更加明显。通过自适应获取阈值T，无需另设参数得到小波紧支撑框架，进而将信号分解成具有最佳中心频率的固有模态分量。

以真空接触器断开时的瞬态信号为例提取信号特征，其步骤如下：

1） 对采样点数为N的瞬态电压信号v(i)(i=1, 2, …, N)实施快速傅里叶变换，得到信号的频谱支持V(x)，x为频率。

2） 在不同尺度步长S下使用高斯滤波函数对V(x)进行卷积滤波，得到V(x)的尺度空间L(x,S)。

式中：n为从−M到M递增的整数；M为足够大的正数，当M=$6 \sqrt{S}+1 $时，尺度空间变换可在减少运算量的同时，确保运算结果的精度^[19]；$g （ {n,S} ） $为高斯核函数。

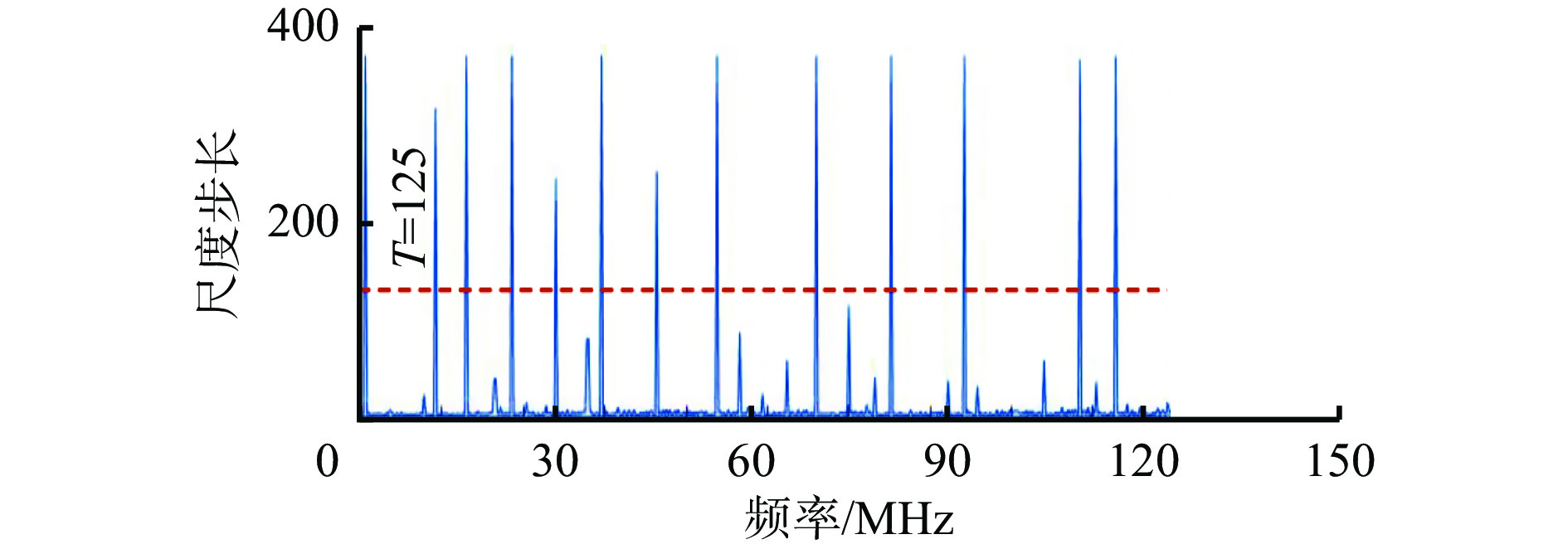
每次滤波后得到更加平滑的频谱，尺度空间L(x, S)中x的局部极小值数量是关于尺度步长S的递减函数。每个初始极小值点都能在尺度空间中生成一条曲线C，如图 3所示。可看出部分曲线随着尺度步长S增大而消失，故可以选择合适的阈值，保留大于阈值有意义的曲线。使用Otsu法获取阈值T，将曲线长度二值化分类，通过遍历最大类间方差得到最佳阈值。

图  3  曲线C的尺度空间分布及阈值

Figure  3.  Scale spatial distribution and threshold of curve C

下载: 全尺寸图片 幻灯片

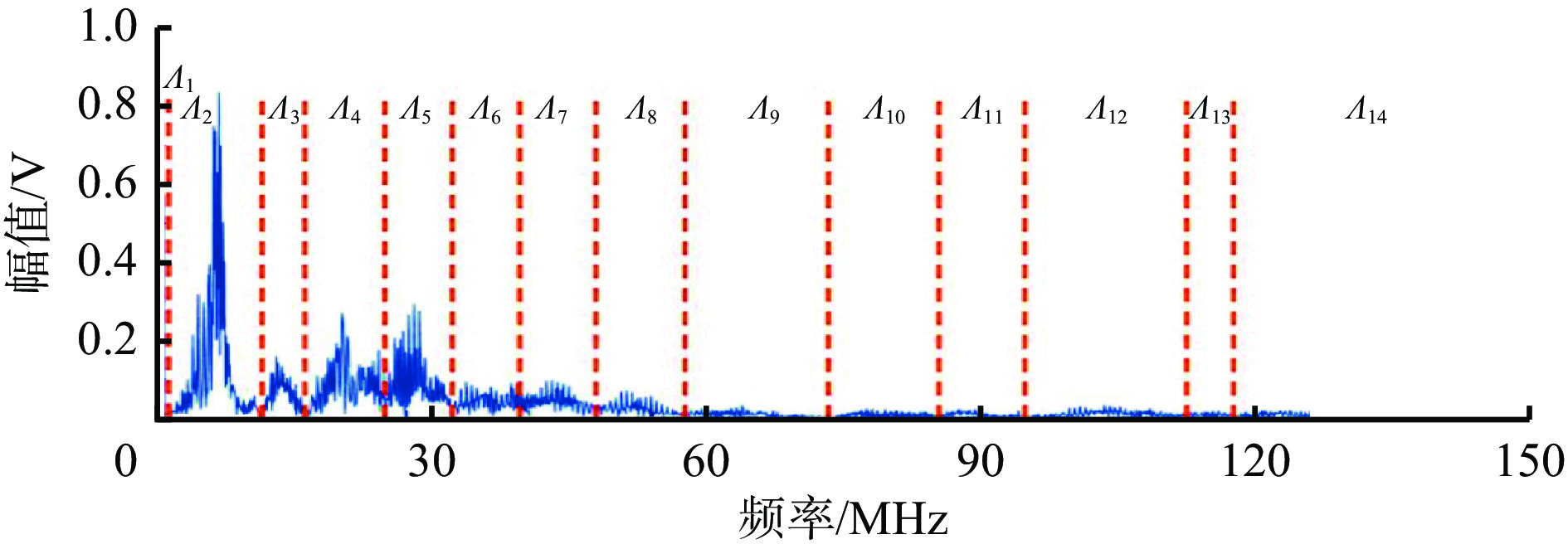
长度超过阈值T的曲线对应图4中瞬态干扰信号频谱分割边界，而小于T的曲线即作为无意义的过切分边界舍弃。由图4可看出，该干扰信号频谱划分为Λ₁−Λ₁₄共14个频带，其中Λ₂−Λ₅频带有大幅峰值，为主导干扰信号频域分布；Λ₆−Λ₉频带幅值较低；后续频段信号微弱。

图  4  干扰信号的频谱图

Figure  4.  Spectrum map of interference signal

下载: 全尺寸图片 幻灯片

3） 将分割后的Z个连续区归一化到[0，π]范围，根据Meyer小波的构造思想，对图4中每段区间Λ_k(k=1，2，…，Z)构造小波紧支撑框架，得到各区间的经验小波函数$ \hat{\psi}_{{{k}}}(\omega) $和经验尺度函数$ \hat{\phi}_{{{k}}}(\omega) $，其中$\omega $为角频率。EWT的细节系数与由经验小波函数与信号作内积生成；近似系数由经验尺度函数与信号作内积生成，进而得到各频带的固有模态分量v_k(i)。

4） 为了准确提取傅里叶频谱中全部瞬态干扰信号的振荡分量频率，需去除白噪声占主导的模态分量。峭度K₄作为归一化的4阶中心矩，可以很好地判断瞬态干扰信号的高斯分布特性，离散化峭度为

式中${\bar v}_{{k}}$为v_k(i)的均值。

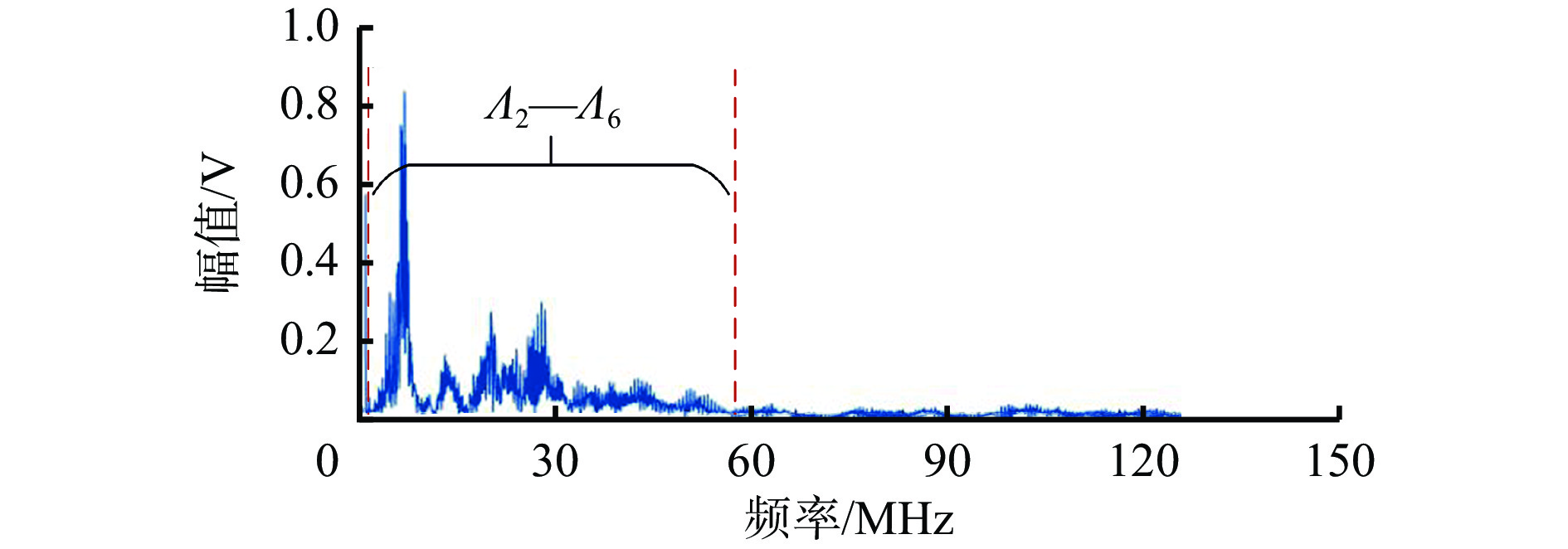
白噪声信号峭度一般小于3，而真空接触器开合产生的干扰信号是一种瞬时、突变的信号，其峭度大于3，将小于3的相邻模态分量合并，视为白噪声。本例中频带Λ₂−Λ₆模态的峭度均大于3，其余频带模态峭度小于3，至此，真空接触器吸合时瞬态干扰信号频域分布为[Λ₂, Λ₆]（图5）。

图  5  瞬态干扰信号频域分布

Figure  5.  Frequency domain distribution of transient interference signal

下载: 全尺寸图片 幻灯片

1.3   实测信号分析

实测数据采样频率为1.25 GHz，并分别截取信号中10 000个采样点进行分析，得到典型频域分布，见表1。

表  1  各开关器件操作干扰信号特征量

Table  1.  Characteristic scale of operation interference signal of each switching device

操作	干扰持续时间/μs	最大幅值/V	频域分布/MHz
外部开关设备上电	2~8	1.5	1.7~66.8
内部真空接触器吸合	120~500	2.0	2.4~55.2
内部真空接触器断开	80~200	1.5	2.9~59.0

下载: 导出CSV 

| 显示表格

由表1可知，外部开关设备上电时产生的干扰持续时间较短，为10 μs以内。而内部真空接触器吸合与断开时产生的干扰持续时间较长，多为100 μs以上。因此，真空接触器操作易造成长时间输出异常，触发电控系统误动作。

真空接触器开合瞬态干扰频域分布集中在2~60 MHz，大体分为2个部分：第1部分范围一般在2~40 MHz，其频域能量占比高，干扰频率稳定且集中在峰值附近，其中真空接触器吸合时集中在9.0，26.8，36.8 MHz附近；真空接触器断开时集中在9.0，20.9，32.7 MHz附近；第2部分能量占比低于第1部分，无明显峰值，范围一般在40~60 MHz。

2.   电控系统稳定性分析

2.1   含寄生参数电路的等效模型

钻机电控系统小信号检测电路设计时选用高带宽增益运算放大器，以提高电路瞬态响应能力，且其在瞬态干扰下对引脚寄生电容更加敏感。当瞬态干扰进入电路中时，电路元件引脚上的寄生电容将在环路中产生新的附加相位，增加了电路输出失效风险，进而导致监测系统误动作。若附加相位α=−180°，电路自激振荡，若α未达到但接近−180°，期间产生的长时间高峰值振铃信号同样严重威胁监测系统安全准确运行。运算放大器使用相位裕度$ {\alpha _m} $表示系统的稳定性，$ {\alpha_m} $典型下限为45°，即环路增益为0时，若附加相移距−180°有45°的裕度，则无输出异常风险^[15]。

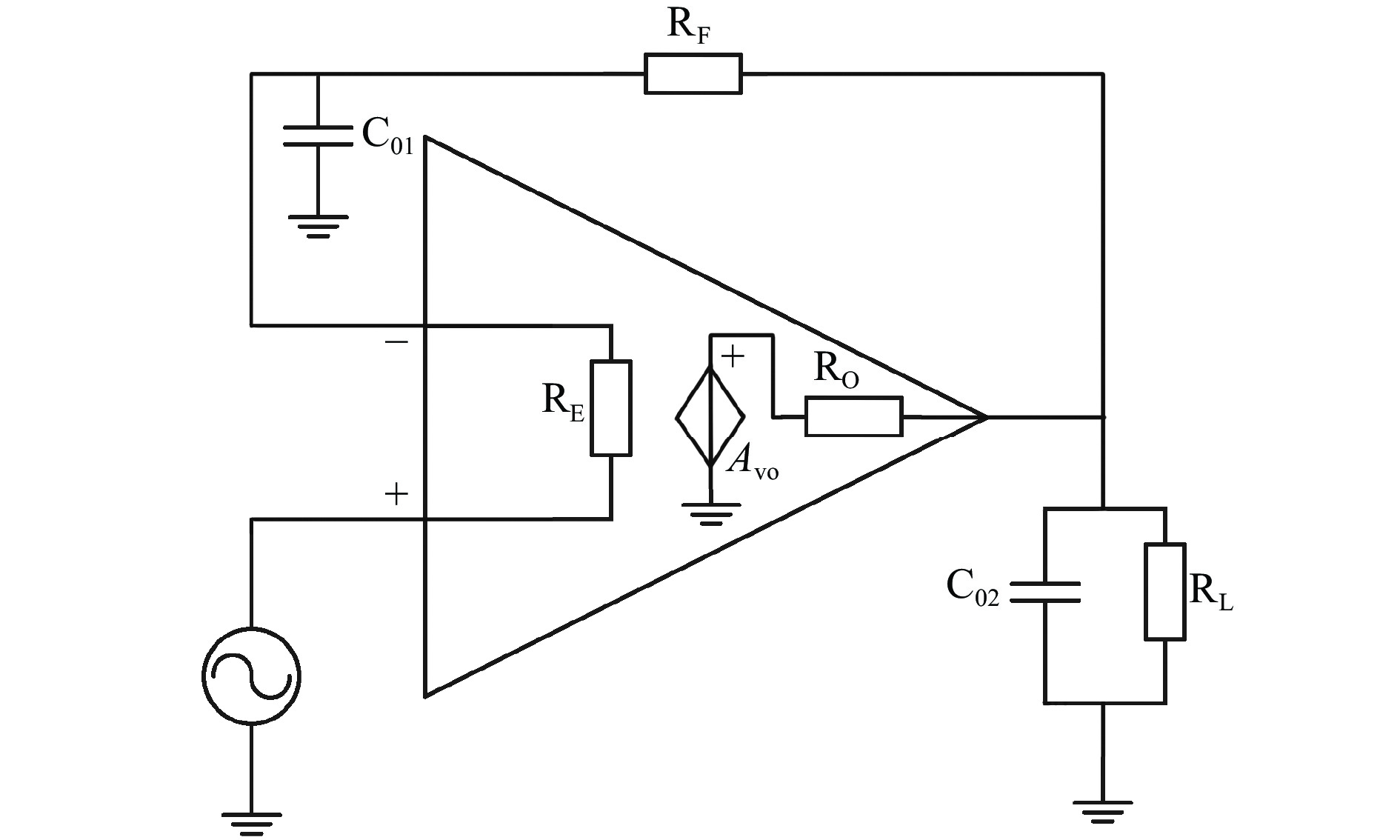
以电流采样电路为例，第1级跟随电路选用OP27高频运算放大器，增益带宽为8 MHz。分析运算放大器的反馈环路时，需要考虑反向输入端与输出端引脚寄生电容的影响，电压跟随电路等效模型如图6所示。其中，R_E为OP27等效输入电阻，R_E=8 MΩ；R_O为放大器等效输出电阻，R_O=70 Ω；R_F为反馈电阻；R_L为后续信号调理电路等效负载电阻；A_vo为开环直流增益；C₀₁与C₀₂为运算放大器反相输入端与输出端的引脚寄生电容。OP27输入端走线长约100 mm，且输入、输出引脚经过多个过孔与焊盘，使用Maxwell软件对放大器输入引脚走线建模分析，其走线寄生电容为34 pF，单个过孔寄生电容估算为0.25 pF。

图  6  电压跟随电路等效模型

Figure  6.  Equivalent model of voltage following circuit

下载: 全尺寸图片 幻灯片

电路环路增益G(s)是反馈系数F(s)与开环增益A(s)的乘积，开环增益A(s)与反馈系数F(s)计算公式为

式中：s为拉普拉斯算子；f₀为主极点频率。

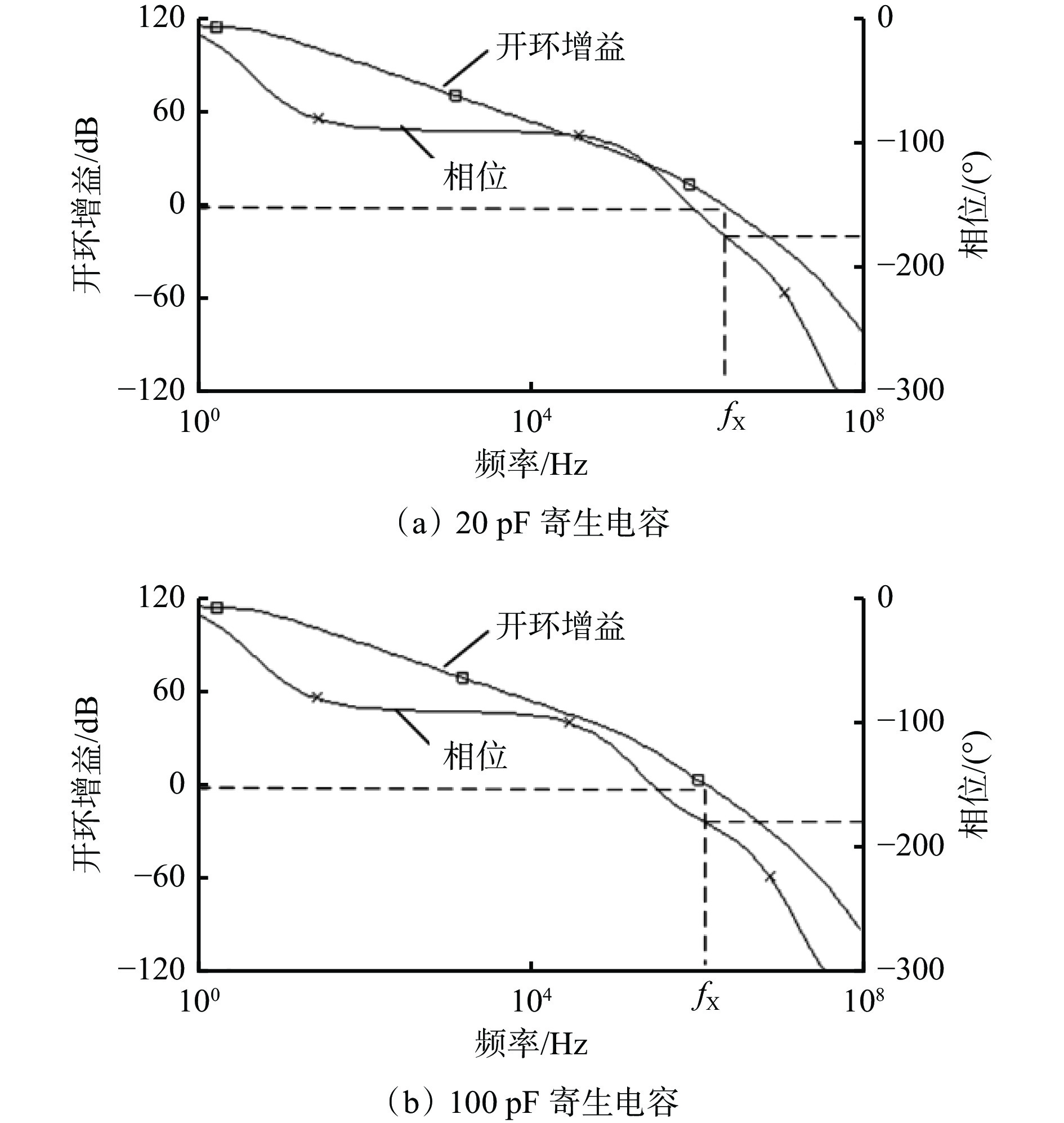
环路增益为0时的频率为f_x，即自激振荡频率。由G(s)可求得环路幅频特性与相频特性曲线，电路无引脚寄生电容时，f_x处附加相位为−109.3°，未达到自激振荡相位条件且相位裕度$ { \alpha _m} $＞45°。

输入端与输出端各存在20，100 pF引脚寄生电容时的仿真结果如图7所示。当寄生电容为20 pF时，f_x处的相位为−174.2°，超出安全范围；当寄生电容为100 pF时，f_x处的相位为−180.3°，达到自激振荡条件。可看出反馈环路中引脚寄生电容的存在使得电路相频特性出现新的极点，增加了反馈环路中的附加相位。

图  7  不同寄生参数时的特性曲线

Figure  7.  Characteristic curve with different parasitic parameters

下载: 全尺寸图片 幻灯片

实际电路中，因敷铜、过孔、走线、引脚焊盘等原因产生的寄生参数难以避免，不同批次的元器件与PCB也存在差别，直接影响小信号电路的稳定性。

2.2   瞬态干扰敏感性分析

环路增益数学模型从频率响应的角度判定系统稳定性，无法展示受扰时域过程。为直观地获取瞬态干扰时域过程，采用OrCAD Capture搭建小信号电路微模型进行仿真，反映瞬态过程电路的敏感性。

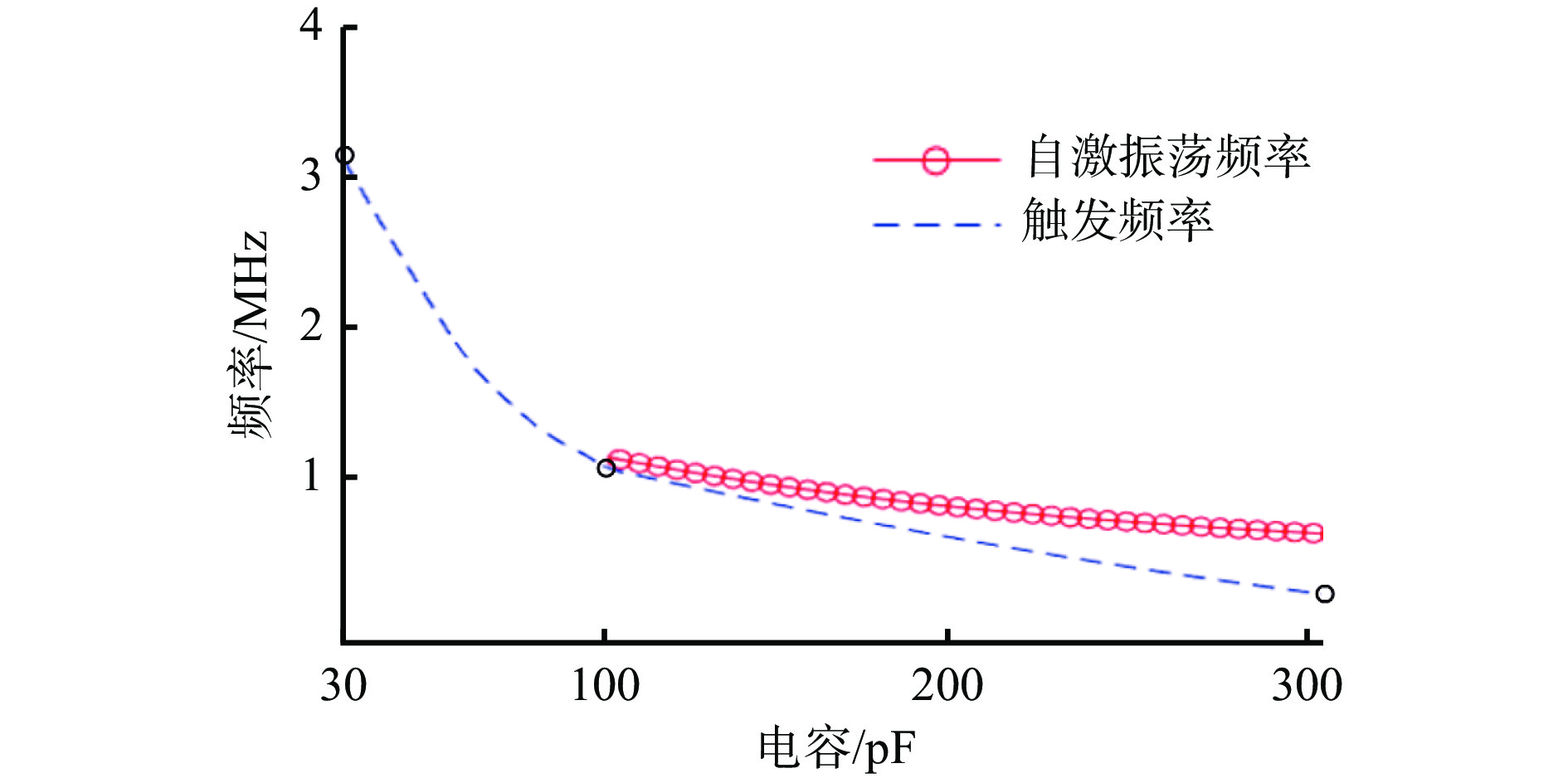
在输入信号中添加阻尼衰减正弦信号模拟瞬态干扰，测试不同引脚寄生电容下输入干扰信号频率与输出信号失效的关系，如图8所示。当引脚寄生电容大于30 pF小于100 pF，输入特定频率以上的干扰信号后，输出信号产生短时振铃。当引脚寄生电容为30 pF，传导进入3.2 MHz以上干扰信号时，输出信号产生10 μs的高幅值振铃，且随着引脚寄生电容增大，振铃信号时间延长，可持续数个工频周期（1个工频周期为0.02 s）。当引脚寄生电容大于100 pF时，输入特定频率以上的干扰信号将导致电路自激振荡。随着引脚寄生电容增大，f_x呈现减小趋势，从1.07 MHz递减到0.57 MHz；同时触发频率迅速减小，从1 MHz递减到0.2 MHz，与f_x的比值从93%降到26%。在瞬态干扰下，电路稳定性随引脚寄生电容增大而下降。

图  8  信号失效触发频率与寄生电容关系

Figure  8.  Relationship between trigger frequency of signal failure and parasitic capacitance

下载: 全尺寸图片 幻灯片

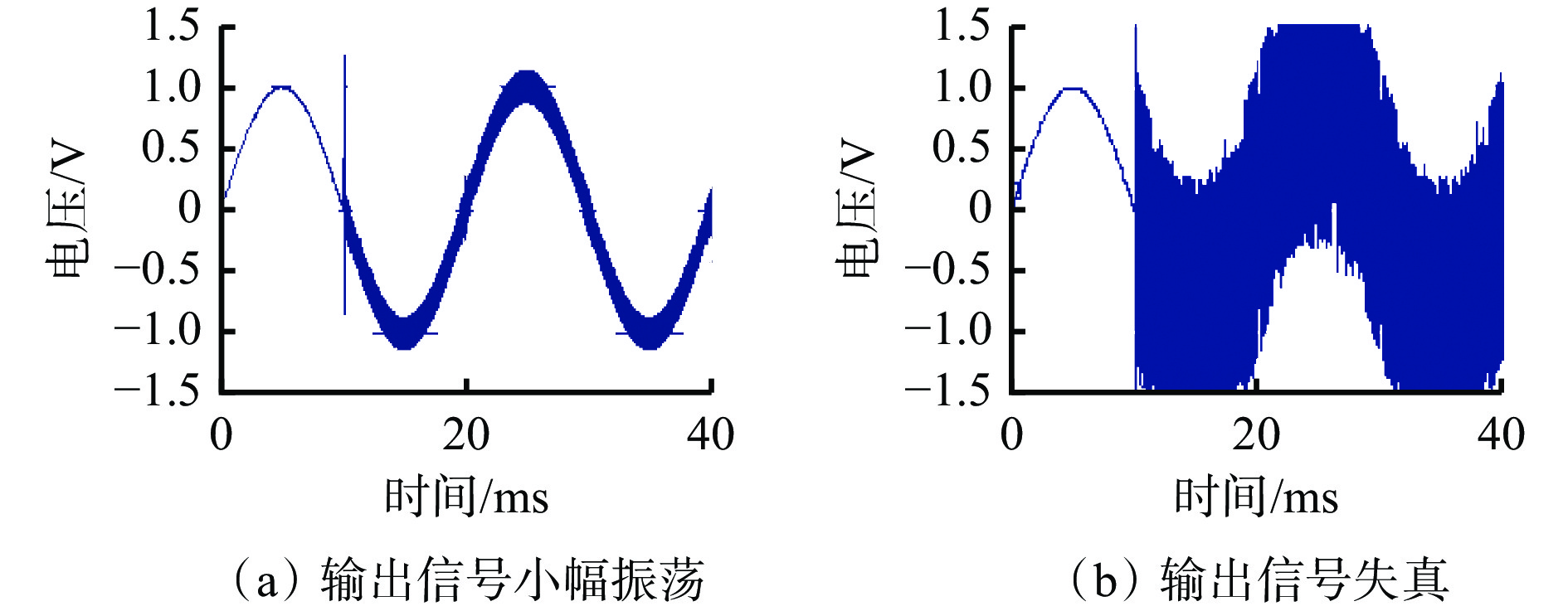
自激振荡程度与输入瞬态干扰频率也紧密相关（图9），当输入瞬态干扰频率达到触发频率时，输出信号出现0.1 V以下小幅振荡；当输入瞬态干扰频率逐渐增大时，输出振荡幅值也迅速增大，直到输出波形失真。

图  9  不同干扰频率下自激振荡输出信号

Figure  9.  Self-excited oscillation output signal under different interference frequencies

下载: 全尺寸图片 幻灯片

现场工况中干扰情况复杂，且敏感电路对瞬态干扰的耐受程度不同。实际电路引脚寄生电容在200 pF以下，因此将0.2 MHz以上频率的干扰信号视为重点滤除频段。

3.   抗干扰设计及试验验证

3.1   二阶滤波电路设计

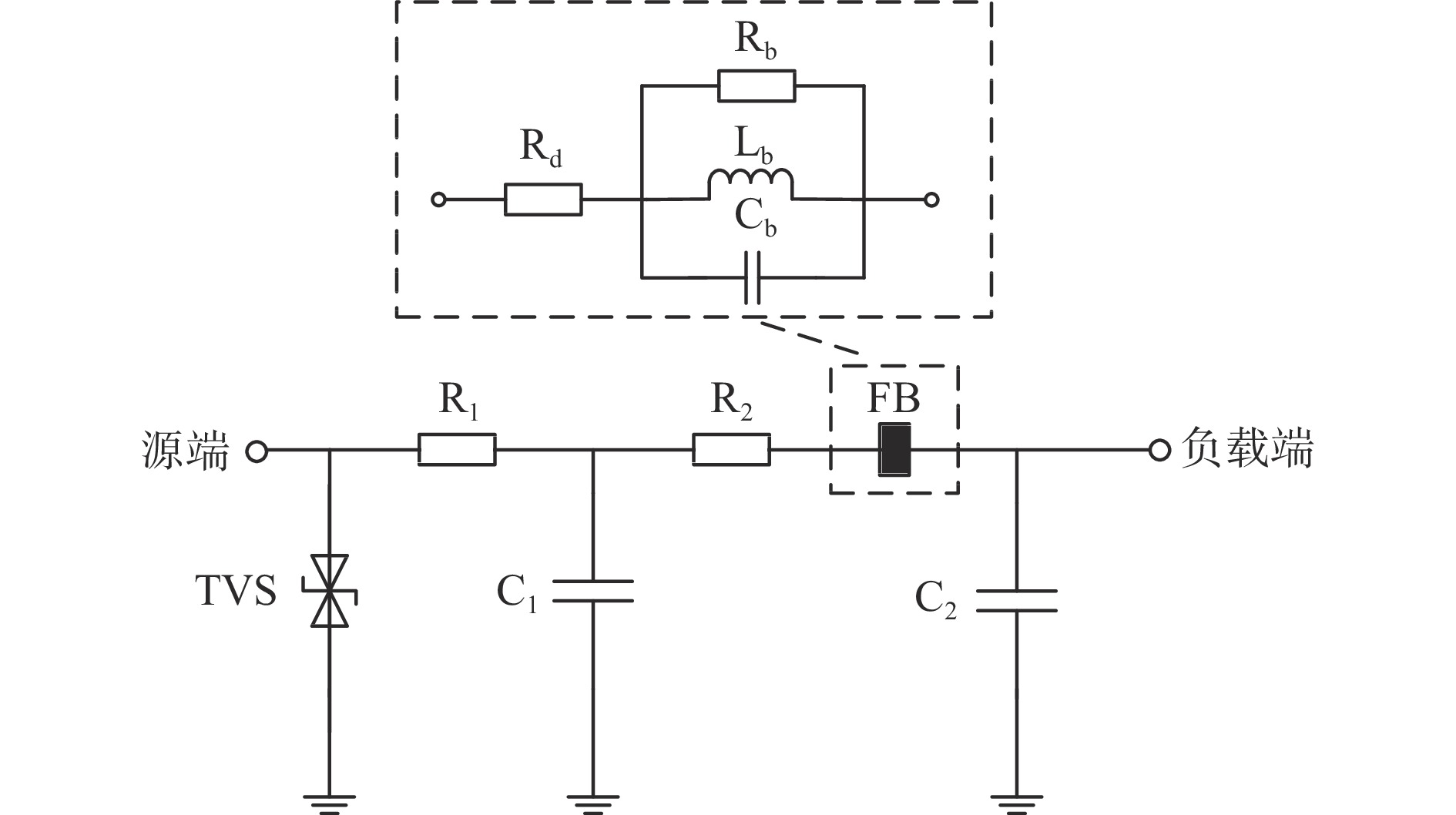
铁氧体磁珠（Ferrite Bead，FB）可近似等效为电阻R_b，R_d，电容C_b，电感L_b组合模型^[20]，其中R_b，C_b，L_b由磁珠内部极间金属板寄生参数决定，R_d=0.025 Ω，在频点附近较宽范围内保持较高阻抗，对高频尖峰吸收效果明显。为此，根据稳定性分析，选取合适频点的磁珠型号，提出一种集二阶滤波和FB为一体的滤波电路，如图10所示。

图  10  二阶滤波电路

Figure  10.  Second order filter circuit

下载: 全尺寸图片 幻灯片

由于互感器源阻抗特性呈低阻抗，放大器负载阻抗特性呈高阻抗，一阶RC滤波电路选用反L形滤波电路结构。在确保监测信号完整的基础上，对敏感频段信号降幅。当电流采样电路进入0.2 MHz以上频率干扰时易导致输出失效，其一阶RC滤波电路截止频率设为0.2 MHz，电阻R₁设为500 Ω，电容C₁取1.6 nF。R₂作用为抑敏感谐振点，经测试选取200 Ω效果最佳。

二阶FB滤波电路，FB选用HB−1T1608−800，其中心频率阻抗为800 Ω，对开关器件启停操作产生2~60 MHz瞬态干扰针对性滤波，确保干扰信号幅值降到安全阈值。电容C₂取5 nF。

3.2   实验室试验

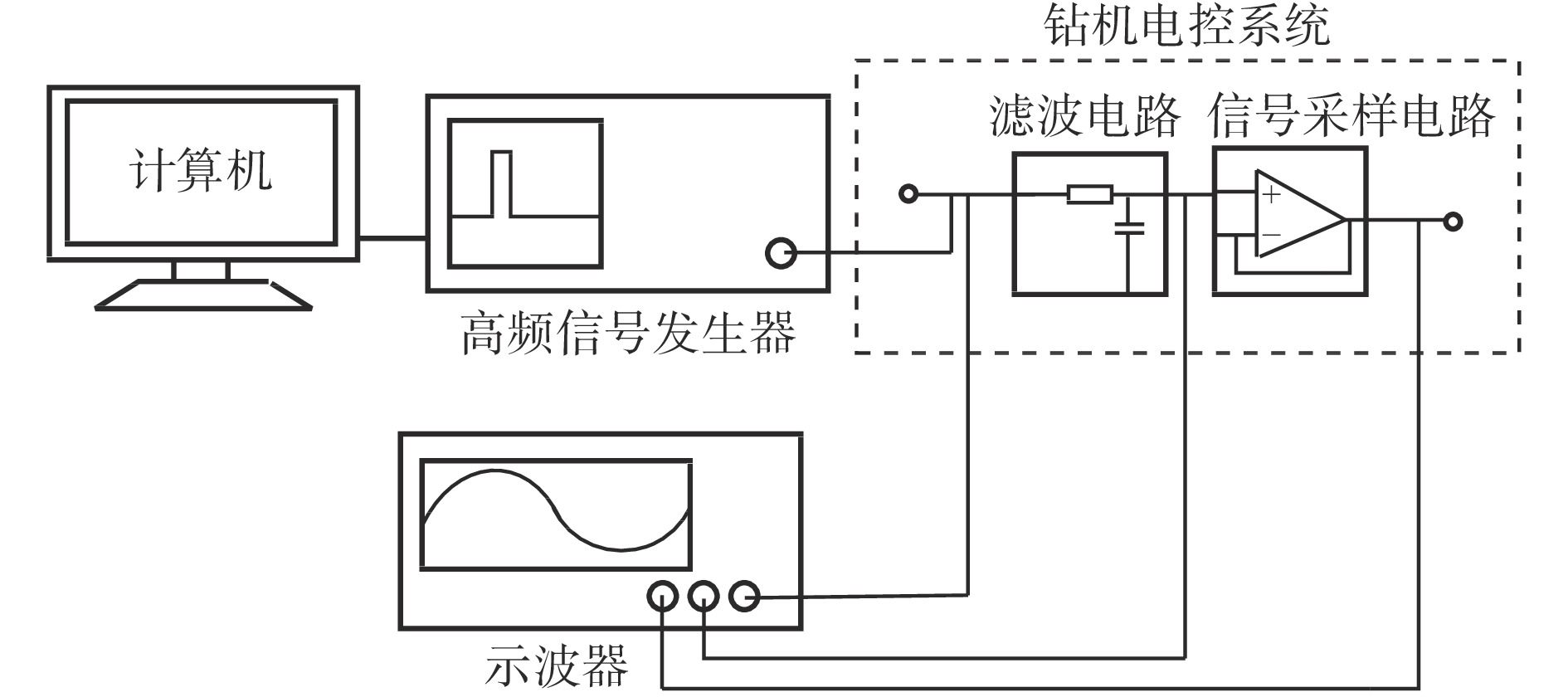
使用IFR2024信号发生器，再现滤波前导致千米钻机电控系统误动作的实测瞬态干扰信号，测试滤波电路干扰抑制效果。试验平台如图11所示。

图  11  实验室试验平台

Figure  11.  Experiment platform in laboratory

下载: 全尺寸图片 幻灯片

滤波电路信号频谱对比如图12所示。可看出经过一阶RC滤波电路后，真空接触器动作时瞬态干扰电压幅值在一定程度上得到抑制，但其频谱在9~30 MHz仍存在−35 dBV以上的干扰信号，造成后续信号采样电路输出振铃异常。当干扰经过含FB的二阶滤波电路后，在信号采样电路敏感的0.2 MHz以上频段，干扰幅值均抑制在−35 dBV以下，信号采样电路无异常输出。

图  12  滤波电路信号频谱对比

Figure  12.  Spectrum comparison diagram of filter circuit signal

下载: 全尺寸图片 幻灯片

3.3   样机运行试验

样机运行试验如图13所示，分别测试各开关器件启停操作下钻机电控系统的稳定性。

图  13  样机运行试验

Figure  13.  Prototype operation test

下载: 全尺寸图片 幻灯片

电控系统二阶滤波电路输入端和输出端信号波形如图14所示。可看出瞬态干扰经过二阶滤波电路后，电压幅值在±0.1 V以内波动。

图  14  瞬态干扰波形

Figure  14.  The transient interference waveform

下载: 全尺寸图片 幻灯片

瞬态干扰频谱如图15所示，可看出真空接触器吸合时，瞬态干扰9.0 MHz附近的最大幅值由−1.7 dBV降低到−42.9 dBV；真空接触器断开时，瞬态干扰20.9 MHz附近的最大幅值由−1.4 dBV降低到−40.5 dBV。

图  15  瞬态干扰频谱

Figure  15.  The transient interference spectrum diagram

下载: 全尺寸图片 幻灯片

信号采样电路敏感的频段内，干扰幅值均抑制在−35 dBV以下，样机运行中二阶滤波电路抗干扰效果与实验室测试中数据基本吻合。运行测试期间钻机电控系统未出现误动作。该设计已在15000型矿用瓦斯抽放智能化定向千米钻机中应用。

4.   结论

1） 对于频域存在强噪声的瞬态干扰信号，使用无参尺度空间表达的EWT算法与峭度判定结合，可得到干扰信号最佳中心频率和分布范围，各开关器件操作时干扰信号频谱在2~60 MHz有多处集中分布。

2） 建立敏感小信号电路模型，揭示了瞬态干扰下电路失效的机理。当输入输出存在30 pF引脚寄生电容，传导进入3.2 MHz以上干扰信号时，输出信号产生10 μs的高幅值振铃，且随着引脚寄生电容增大振铃信号时间延长，可持续数个工频周期。

3） 根据干扰分析结果，制定FB与二阶滤波电路结合的抗干扰措施。实验室试验结果表明，当干扰经过含FB的二阶滤波电路后，在信号采样电路敏感的0.2 MHz以上频段，干扰幅值均抑制在−35 dBV以下，信号采样电路无异常输出。

4） 信号采样电路敏感的频段内，干扰幅值均抑制在−35 dBV以下，样机运行中二阶滤波电路抗干扰效果与实验室试验数据基本吻合。