面向大型数据集的局部敏感哈希K−means算法

魏峰; 马龙

doi:10.13272/j.issn.1671-251x.2022080018

面向大型数据集的局部敏感哈希K−means算法

魏峰^{1, 2,},
马龙^{1, 2, ,}

1.
煤炭科学技术研究院有限公司, 北京　100013
2.
煤炭资源高效开采与洁净利用国家重点实验室, 北京　100013

基金项目: 国家重点研发计划资助项目（2021YFB3201905）。

详细信息

作者简介:
魏峰（1981—），男，山西太原人，研究员，硕士，现主要从事煤矿智能安全监测系统等方面的研究工作，E-mail：weifeng829@163.com

通讯作者:
马龙（1989—），男，山西孝义人，助理研究员，博士，主要研究方向为数据挖掘、煤矿机器人技术，E-mail：444647811@qq.com

中图分类号: TD67
计量
- 文章访问数: 313
- HTML全文浏览量: 63
- PDF下载量: 21
出版历程
- 收稿日期: 2022-08-04
- 修回日期: 2023-03-09
- 网络出版日期: 2022-10-24
- 刊出日期: 2023-03-24

Locality-sensitive hashing K-means algorithm for large-scale datasets

WEI Feng^{1, 2,},
MA Long^{1, 2, ,}

1.
CCTEG China Coal Research Institute, Beijing 100013, China
2.
National Key Lab of Coal Resources High Efficient Mining and Clean Utilization, Beijing 100013, China

摘要

摘要: 大型数据集高效处理策略是煤矿安全监测智能化、采掘智能化等煤矿智能化建设的关键支撑。针对K−means算法面对大型数据集时聚类高效性及准确性不足的问题，提出了一种基于局部敏感哈希（LSH）的高效K−means聚类算法。基于LSH对抽样过程进行优化，提出了数据组构建算法LSH−G，将大型数据集合理划分为子数据组，并对数据集中的噪声点进行有效删除；基于LSH−G算法优化密度偏差抽样（DBS）算法中的子数据组划分过程，提出了数据组抽样算法LSH−GD，使样本集能更真实地反映原始数据集的分布规律；在此基础上，通过K−means算法对生成的样本集进行聚类，实现较低时间复杂度情况下从大型数据集中高效挖掘有效数据。实验结果表明：由10个AND操作与8个OR操作组成的级联组合为最优级联组合，得到的类中心误差平方和（SSEC）最小；在人工数据集上，与基于多层随机抽样（M−SRS）的K−means算法、基于DBS的K−means算法及基于网格密度偏差抽样（G−DBS）的K−means算法相比，基于LSH−GD的K−means算法在聚类准确性方面的平均提升幅度分别为56.63%、54.59%及25.34%，在聚类高效性方面的平均提升幅度分别为27.26%、16.81%及7.07%；在UCI标准数据集上，基于LSH−GD的K−means聚类算法获得的SSEC与CPU消耗时间（CPU−C）均为最优。
- 智慧矿山 /
- 大型数据集 /
- K−means聚类 /
- 局部敏感哈希 /
- 噪声点筛选 /
- 密度偏差抽样
Abstract: Efficient processing strategy for large datasets is a key support for coal mine intelligent constructions, such as the intelligent construction of coal mine safety monitoring and mining. To address the problem of insufficient clustering efficiency and accuracy of the K-means algorithm for large datasets, a highly efficient K-means clustering algorithm based on locality-sensitive hashing (LSH) is proposed. Based on LSH, the sampling process is optimized, and a data grouping algorithm LSH-G is proposed. The large dataset is divided into subgroups and the noisy points in the dataset are removed effectively. Based on LSH-G, the subgroup division process in the density biased sampling (DBS) algorithm is optimized. And a data group sampling algorithm, LSH-GD, is proposed. The sample set can more accurately reflect the distribution law of the original dataset. On this basis, the K-means algorithm is used to cluster the generated sample set, achieving efficient mining of effective data from large datasets with low time complexity. The experimental results show that the optimal cascade combination consists of 10 AND operations and 8 OR operations, resulting in the smallest sum of squares due to error of class center (SSEC). On the artificial dataset, compared with the K-means algorithm based on multi-layer simple random sampling (M-SRS), the K-means algorithm based on DBS, and the K-means algorithm based on grid density biased sampling (G-DBS), the K-means algorithm based on LSH-GD achieves an average improvement of 56.63%, 54.59%, and 25.34% respectively in clustering accuracy. The proposed algorithm achieves an average improvement of 27.26%, 16.81%, and 7.07% in clustering efficiency respectively. On the UCI standard dataset, the K-means clustering algorithm based on LSH-GD obtains optimal SSEC and CPU time consumption (CPU-C).
- intelligent mine /
- large-scale dataset /
- K-means clustering /
- locality-sensitive hashing /
- noise point filtering /
- density biased sampling

HTML全文

图 1 $ \left( {{d_1},{d_2},{p_1},{p_2}} \right) $敏感哈希函数的概率分布

Figure 1. Probability distribution of sensitive hashing function $ \left( {{d_1},{d_2},{p_1},{p_2}} \right) $

下载: 全尺寸图片幻灯片

图 2 不同级联数量情况下LSH−G算法筛选出的数据点噪声变化

Figure 2. Noise variation of data points screened by LSH-G algorithm under different cascade numbers

下载: 全尺寸图片幻灯片

图 3 进行10%抽样后得到的样本集

Figure 3. Sample set obtained after 10% sampling

下载: 全尺寸图片幻灯片

图 4 数据量变化对聚类准确性的影响

Figure 4. Impact of data size change on clustering accuracy

下载: 全尺寸图片幻灯片

图 5 数据维度变化对聚类准确性的影响

Figure 5. Impact of data dimension change on clustering accuracy

下载: 全尺寸图片幻灯片

图 6 数据类个数变化对聚类准确性的影响

Figure 6. Impact of data class number change on clustering accuracy

下载: 全尺寸图片幻灯片

图 7 数据量变化对聚类高效性的影响

Figure 7. Impact of data size change on clustering efficiency

下载: 全尺寸图片幻灯片

图 8 数据维度变化对聚类高效性的影响

Figure 8. Impact of data dimension change on clustering efficiency

下载: 全尺寸图片幻灯片

图 9 数据类个数变化对聚类高效性的影响

Figure 9. Impact of data class number change on clustering efficiency

下载: 全尺寸图片幻灯片

表 1 测试数据集特征

Table 1 Test dataset characteristics

编号	数据集名称	数据量/个	维度	类个数
1	数据集1	20 000	5	3
2	数据集2	40 000	5	3
3	数据集3	60 000	5	3
4	数据集4	80 000	5	3
5	数据集5	120 000	5	3
6	数据集6	220 000	5	3
7	数据集7	40 000	10	3
8	数据集8	40 000	15	3
9	数据集9	40 000	20	3
10	数据集10	40 000	40	3
11	数据集11	40 000	5	6
12	数据集12	40 000	5	9
13	数据集13	40 000	5	12
14	数据集14	40 000	5	27
15	Pen−based	10 992	16	10
16	Shuttle	14 500	9	7
17	Magic	19 020	10	2
18	Letter Recognition	20 000	16	26
19	Statlog	58 000	9	5

下载: 导出CSV

表 2 不同级联组合下19个样本集的SSEC

Table 2 The SSEC of 19 sample sets under different cascaded combinations

A	SSEC
A	O=1	O=2	O=3	O=4	O=5	O=6	O=7	O=8	O=9	O=10
1	11.625	11.080	10.325	9.685	9.072	8.586	7.941	7.313	6.841	6.309
2	10.954	10.606	9.852	9.258	8.695	8.181	7.529	6.997	6.358	5.879
3	10.107	9.758	9.355	8.857	8.581	7.885	7.284	6.622	6.021	5.514
4	9.282	9.041	8.758	8.586	8.299	7.602	7.085	6.498	5.884	5.392
5	8.354	7.911	7.689	7.326	7.281	6.989	6.651	6.185	5.646	5.218
6	7.059	6.882	6.711	6.632	6.498	6.286	5.989	5.714	5.327	4.881
7	5.944	5.801	5.693	5.389	5.154	4.997	4.727	4.589	4.301	4.082
8	4.736	4.688	4.512	4.387	4.097	3.827	3.581	3.158	2.929	2.897
9	3.935	3.559	3.332	3.201	3.023	2.835	2.606	2.483	2.298	2.255
10	3.103	3.022	2.915	2.801	2.684	2.537	2.463	2.142	2.197	2.205

下载: 导出CSV

表 3 不同数据量数据集的SSEC

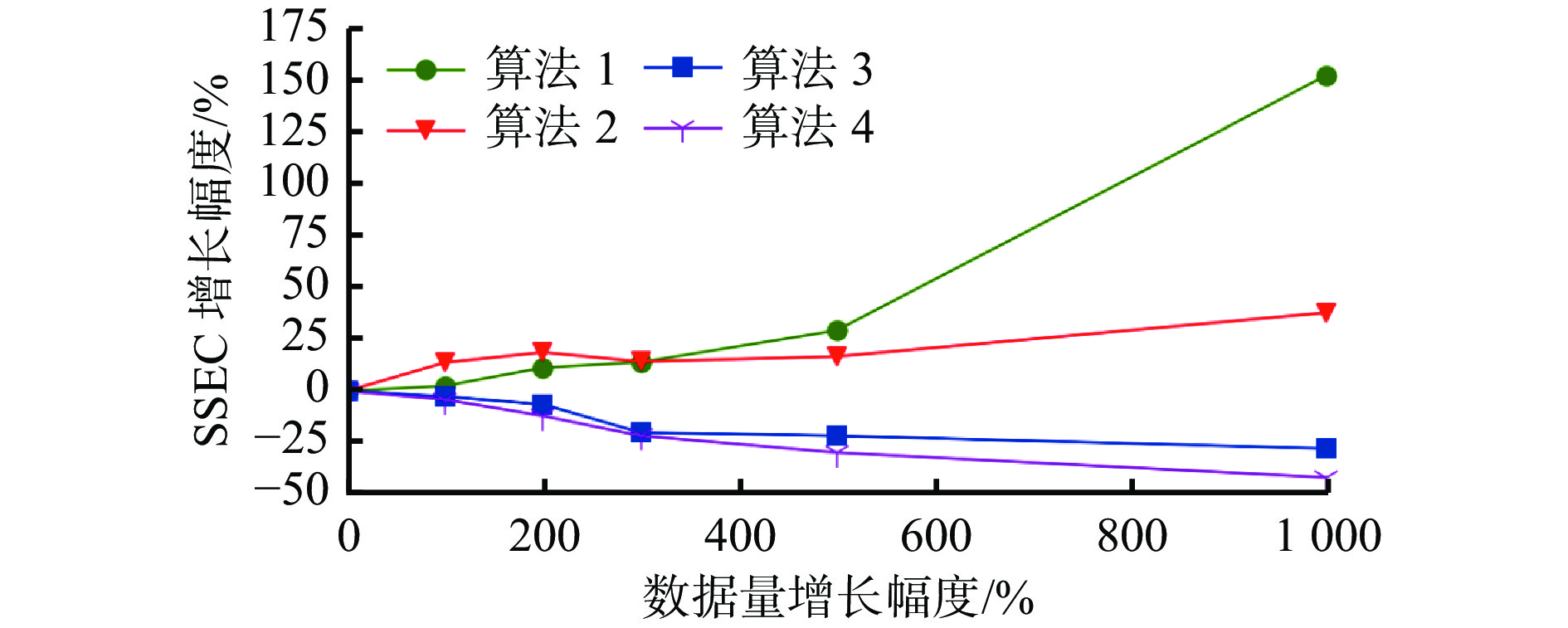
Table 3 The SSEC of datasets with different data size

数据集序号	数据量	SSEC
数据集序号	数据量	算法1	算法2	算法3	算法4
1	20000	0.0812	0.0686	0.0628	0.0527
2	40000	0.0832	0.0781	0.0611	0.0505
3	60000	0.0904	0.0815	0.0587	0.0463
4	80000	0.0926	0.0784	0.0501	0.0412
5	120000	0.1051	0.0801	0.0491	0.0369
6	220000	0.2057	0.0947	0.0452	0.0305

下载: 导出CSV

表 4 不同维度数据集的SSEC

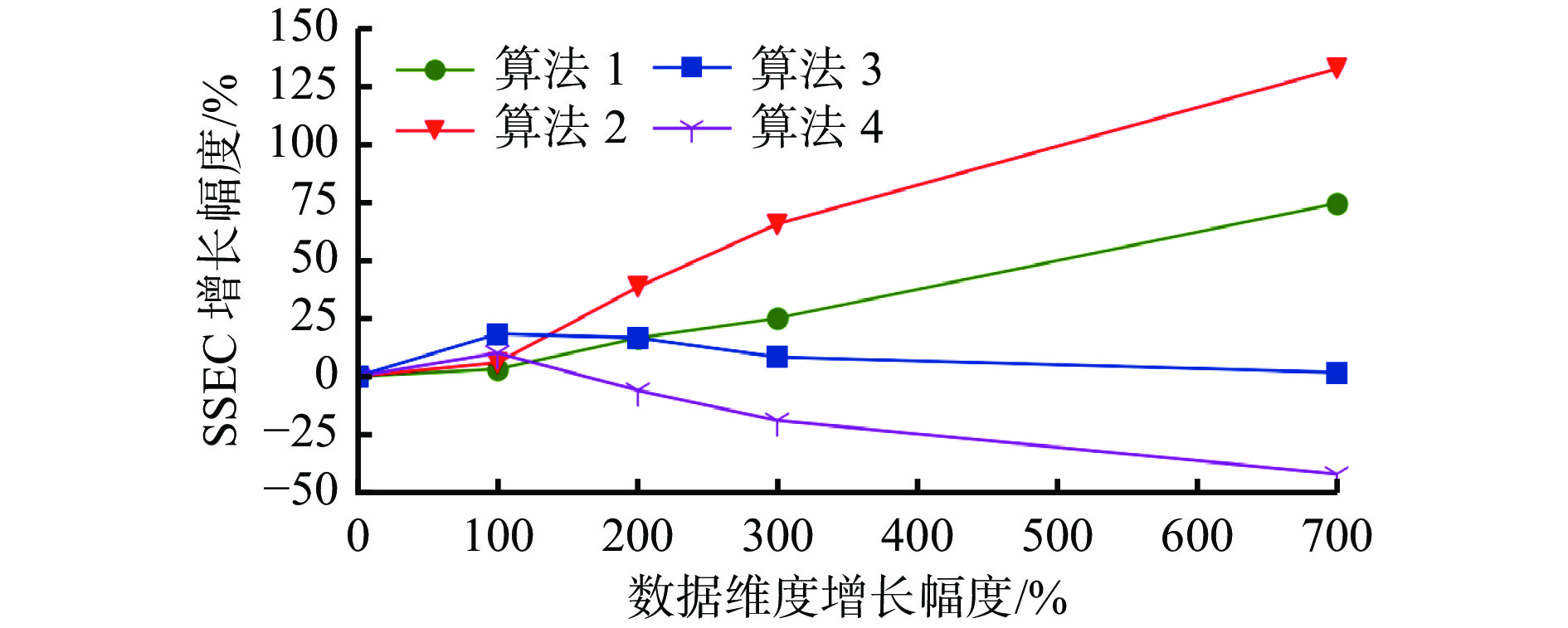
Table 4 The SSEC of datasets with different dimensions

数据集序号	维度	平均SSEC
数据集序号	维度	算法1	算法2	算法3	算法4
2	5	0.0166	0.0156	0.0122	0.0101
7	10	0.0171	0.0165	0.0144	0.0111
8	15	0.0193	0.0215	0.0142	0.0095
9	20	0.0207	0.0257	0.0132	0.0082
10	40	0.0288	0.0360	0.0124	0.0059

下载: 导出CSV

表 5 不同类个数数据集的SSEC

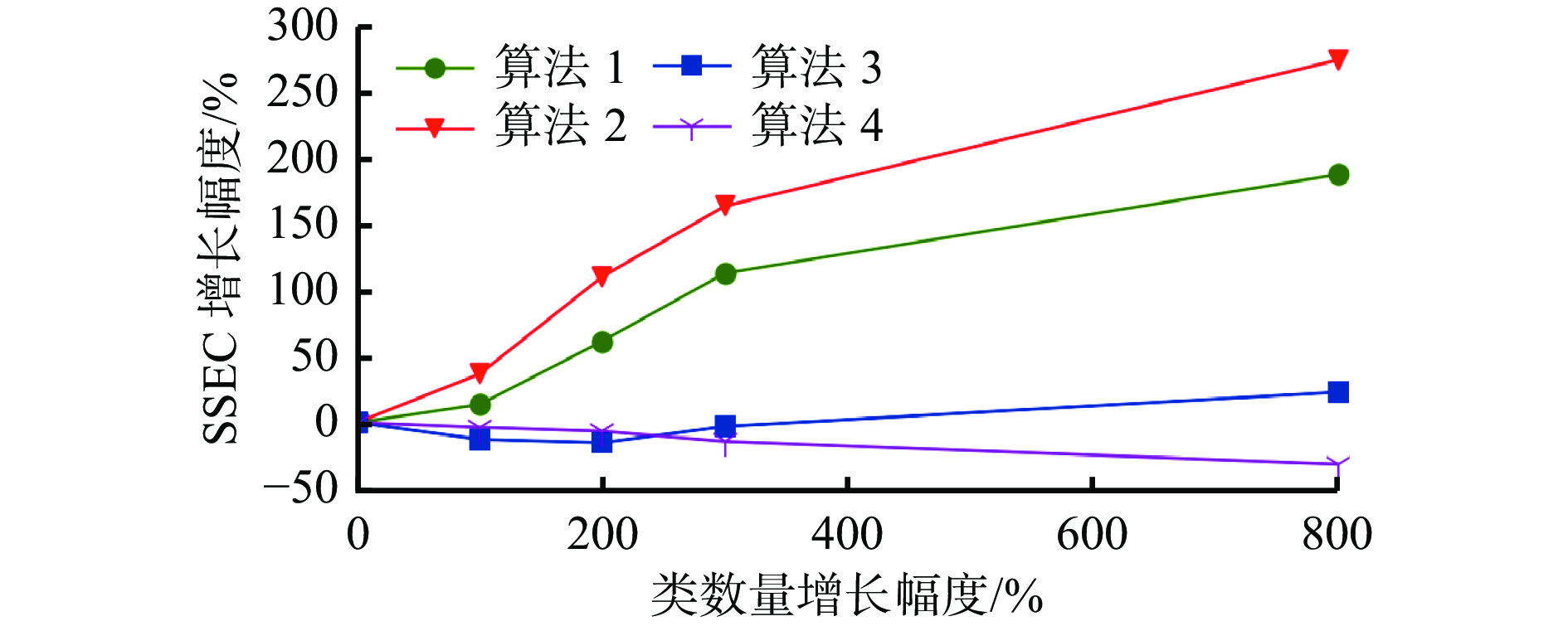
Table 5 The SSEC of datasets with different number of data class

数据集序号	类个数	平均SSEC
数据集序号	类个数	算法1	算法2	算法3	算法4
2	3	0.0277	0.0260	0.0204	0.0168
11	6	0.0315	0.0356	0.0178	0.0162
12	9	0.0448	0.0548	0.0173	0.0157
13	12	0.0591	0.0687	0.0198	0.0154
14	27	0.0798	0.0975	0.0251	0.0115

下载: 导出CSV

表 6 不同数据量数据集的CPU−C

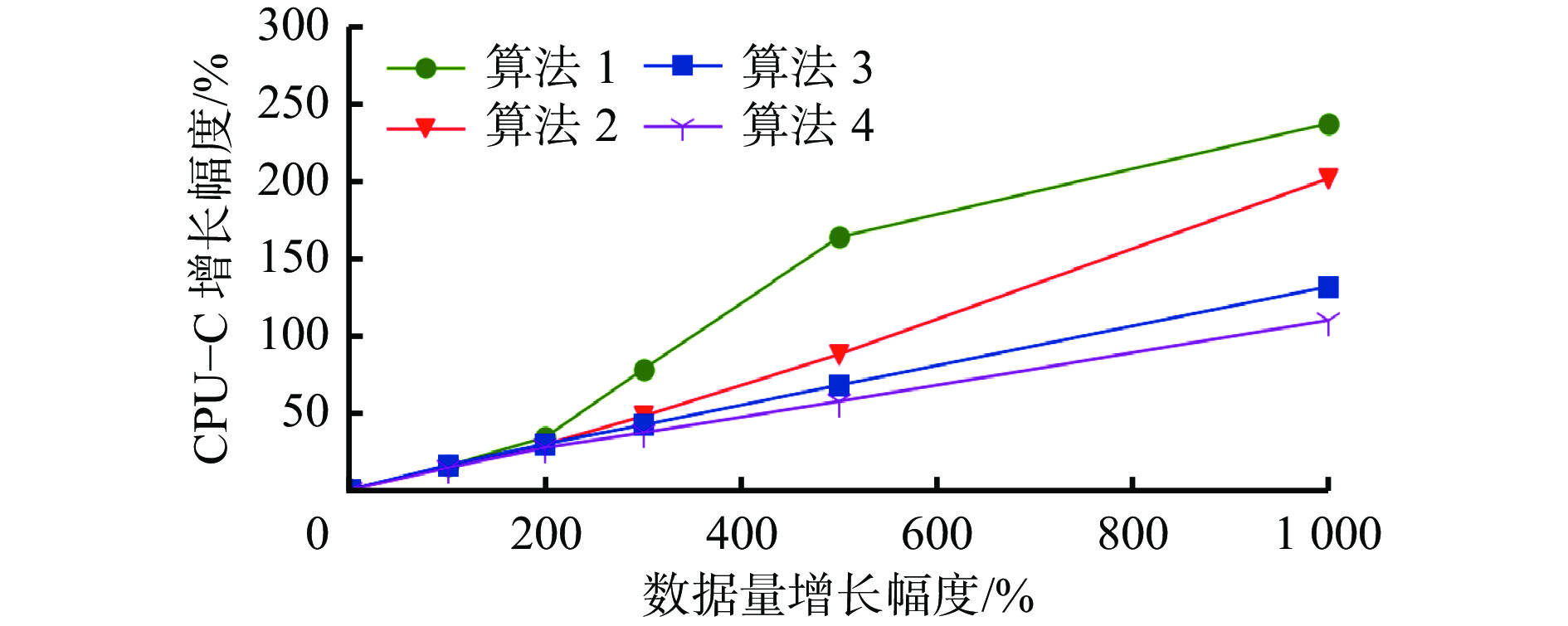
Table 6 The CPU-C of datasets with different data size

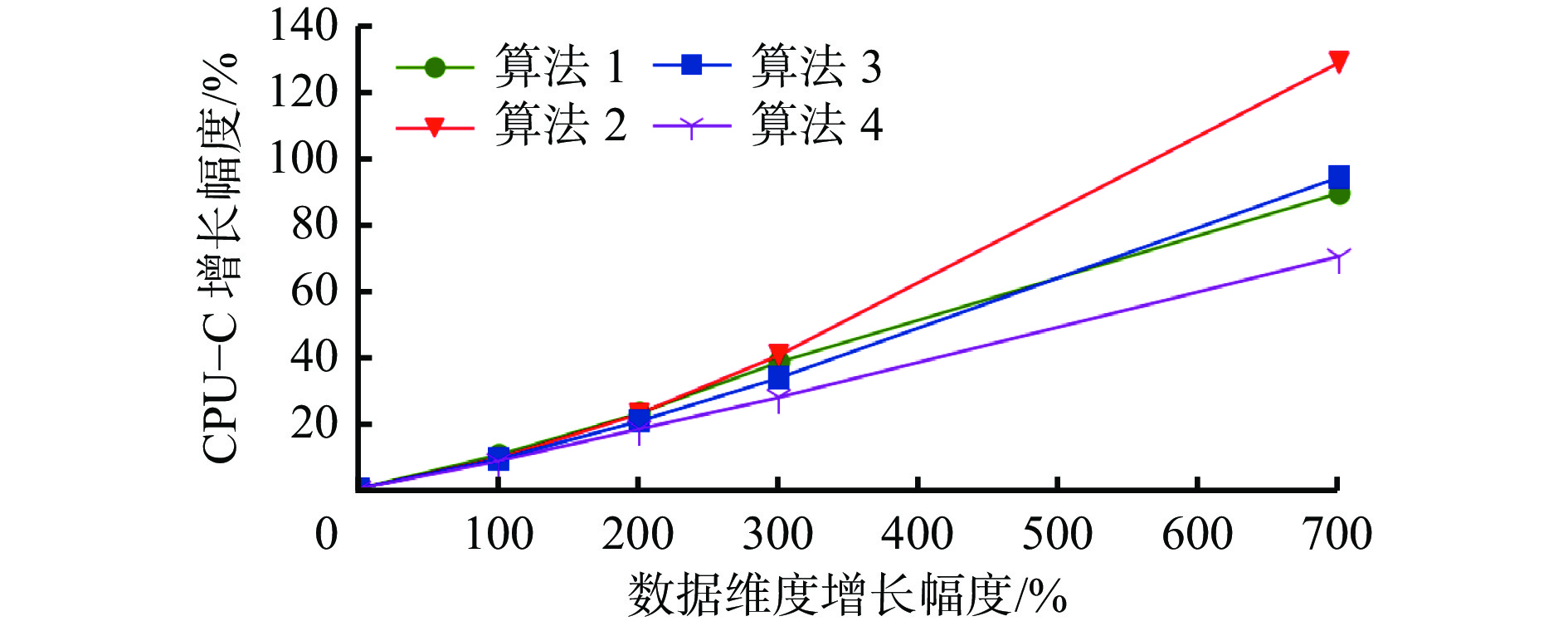
数据集序号	数据量	CPU−C/s
数据集序号	数据量	算法1	算法2	算法3	算法4
1	20000	4.782	3.964	3.728	3.697
2	40000	5.525	4.698	4.388	4.171
3	60000	6.413	6.422	6.132	5.981
4	80000	8.522	7.335	6.716	6.435
5	120000	12.606	9.318	7.931	7.386
6	220000	16.131	14.969	10.949	9.852

下载: 导出CSV

表 7 不同数据维度数据集的CPU−C

Table 7 The CPU-C of dataset with different dimensions

数据集序号	维度	CPU−C/s
数据集序号	维度	算法1	算法2	算法3	算法4
2	5	5.525	4.698	4.388	4.171
7	10	6.091	5.131	4.779	4.433
8	15	6.788	5.764	5.286	4.825
9	20	7.645	6.598	5.862	5.276
10	40	10.481	10.771	8.535	7.411

下载: 导出CSV

表 8 不同类个数数据集的CPU−C

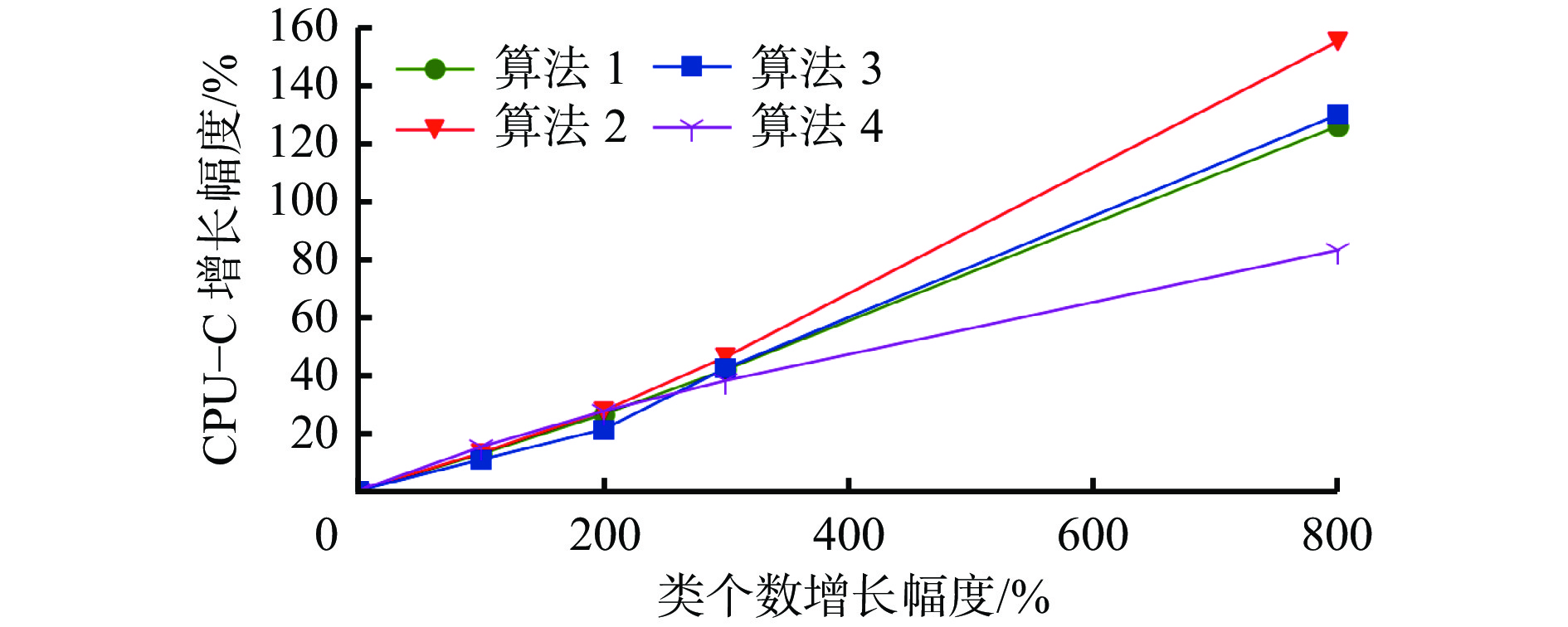
Table 8 The CPU-C of datasets with different number of class

数据集序号	类个数	CPU−C/s
数据集序号	类个数	算法1	算法2	算法3	算法4
2	3	5.525	4.698	4.388	4.171
11	6	6.223	5.308	4.858	4.801
12	9	6.981	5.991	5.403	5.314
13	12	7.831	6.866	6.286	5.757
14	27	12.481	11.986	9.997	7.634

下载: 导出CSV

表 9 4种算法在UCI标准数据集上的SSEC与CPU−C

Table 9 The SSEC and CPU-C of 4 algorithms on the UCI standard dataset

数据集	算法1		算法2		算法3		算法4
数据集	SSEC	CPU−C/s	SSEC	CPU−C/s	SSEC	CPU−C/s	SSEC	CPU−C/s
Pen-based	6298.23	13.691	6717.08	13.083	5916.74	12.626	5495.61	11.764
Shuttle	2965.14	11.972	3117.25	10.836	2403.87	10.491	2214.66	10.037
Magic	2584.62	10.131	2615.54	9.451	2478.77	9.077	2398.23	8.235
Letter Recognition	1098.25	15.799	1311.87	14.082	1027.25	13.221	936.48	11.943
Statlog	2574.18	14.821	2724.83	13.187	2315.25	11.842	2080.54	10.294

下载: 导出CSV

参考文献(21)

[1]	杜毅博,赵国瑞,巩师鑫. 智能化煤矿大数据平台架构及数据处理关键技术研究[J]. 煤炭科学技术,2020,48(7):177-185. DOI: 10.13199/j.cnki.cst.2020.07.018 DU Yibo,ZHAO Guorui,GONG Shixin. Study on big data platform architecture of intelligent coal mine and key technologies of data processing[J]. Coal Science and Technology,2020,48(7):177-185. DOI: 10.13199/j.cnki.cst.2020.07.018
[2]	武福生,卜滕滕,王璐. 煤矿安全智能化及其关键技术[J]. 工矿自动化,2021,47(9):108-112. DOI: 10.13272/j.issn.1671-251x.17833 WU Fusheng,BU Tengteng,WANG Lu. Coal mine safety intelligence and key technologies[J]. Industry and Mine Automation,2021,47(9):108-112. DOI: 10.13272/j.issn.1671-251x.17833
[3]	胡青松,张赫男,李世银,等. 基于大数据与AI驱动的智能煤矿目标位置服务技术[J]. 煤炭科学技术,2020,48(8):121-130. DOI: 10.13199/j.cnki.cst.2020.08.015 HU Qingsong,ZHANG Henan,LI Shiyin,et al. Intelligent coal mine target location service technology based on big data and AI driven[J]. Coal Science and Technology,2020,48(8):121-130. DOI: 10.13199/j.cnki.cst.2020.08.015
[4]	MAYA G P S,CHINTALA B R. Big data challenges and opportunities in agriculture[J]. International Journal of Agricultural and Environmental Information Systems,2020,11(1):48-66. DOI: 10.4018/IJAEIS.2020010103
[5]	叶鸥,窦晓熠,付燕,等. 融合轻量级网络和双重注意力机制的煤块检测方法[J]. 工矿自动化,2021,47(12):75-80. DOI: 10.13272/j.issn.1671-251x.2021030075 YE Ou,DOU Xiaoyi,FU Yan,et al. Coal block detection method integrating lightweight network and dual attention mechanism[J]. Industry and Mine Automation,2021,47(12):75-80. DOI: 10.13272/j.issn.1671-251x.2021030075
[6]	温瑞英,王红勇. 基于因子分析和K−means聚类的空中交通复杂性评价[J]. 太原理工大学学报,2016,47(3):384-388,404. DOI: 10.16355/j.cnki.issn1007-9432tyut.2016.03.020 WEN Ruiying,WANG Hongyong. Evaluation of air traffic complexity based on factor analysis and K-means clustering[J]. Journal of Taiyuan University of Technology,2016,47(3):384-388,404. DOI: 10.16355/j.cnki.issn1007-9432tyut.2016.03.020
[7]	SINAGA K P,YANG M-S. Unsupervised K-means clustering algorithm[J]. IEEE Access,2020,8:80716-80727. DOI: 10.1109/ACCESS.2020.2988796
[8]	BAIG A,MASOOD S,TARRAY T A. Improved class of difference-type estimators for population median in survey sampling[J]. Communications in Statistics-Theory and Methods,2019,49(23):5778-5793.
[9]	LIAO Kaiyang,LIU Guizhong. An efficient content based video copy detection using the sample based hierarchical adaptive k-means clustering[J]. Journal of Intelligent Information Systems,2015,44(1):133-158. DOI: 10.1007/s10844-014-0332-5
[10]	PALMER C R,FALOUTSOS C. Density biased sampling:an improved method for data mining and clustering[J]. ACM SIGMOD Record,2000,29(2):82-92. DOI: 10.1145/335191.335384
[11]	HUANG Jianbin,SUN Heli,KANG Jianmei,et al. ESC:an efficient synchronization-based clustering algorithm[J]. Knowledge-Based Systems,2013,40:111-122. DOI: 10.1016/j.knosys.2012.11.015
[12]	MINAEI-BIDGOLI B,PARVIN H,ALINEJAD-ROKNY H,et al. Effects of resampling method and adaptation on clustering ensemble efficacy[J]. Artificial Intelligence Review,2014,41(1):27-48. DOI: 10.1007/s10462-011-9295-x
[13]	AGGARWAL A, DESHPANDE A, KANNAN R. Adaptive sampling for K-means clustering[C]. 12th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems/13th International Workshop on Randomization and Computation, Berkeley, 2009: 15-28.
[14]	KUMAR K M,REDDY A R M. An efficient K-means clustering filtering algorithm using density based initial cluster centers[J]. Information Sciences,2017,418/419:286-301. DOI: 10.1016/j.ins.2017.07.036
[15]	SÁEZ J A,KRAWCZYK B,WOŹNIAK M. Analyzing the oversampling of different classes and types of examples in multi-class imbalanced datasets[J]. Pattern Recognition,2016,57:164-178. DOI: 10.1016/j.patcog.2016.03.012
[16]	胡欢. 多维数据上近似聚集和最近邻查询的高效算法[D]. 哈尔滨: 哈尔滨工业大学, 2021. HU Huan. Efficient algorithms for approximate aggregation and nearest neighbor queries over multi-dimensional data[D]. Harbin: Harbin Institute of Technology, 2021.
[17]	李建忠. 面向社交网络的科技领域事件检测系统的研究与实现[D]. 西安: 西安电子科技大学, 2019. LI Jianzhong. Researches and implementation of technology event detection in social networks[D]. Xi'an: Xidian University, 2019.
[18]	周萌. 基于多粒度级联森林哈希学习的图像检索[D]. 重庆: 重庆邮电大学, 2019. ZHOU Meng. Multi-grained cascade forest based hashing for image retrieval[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2019.
[19]	NELSON K P,THISTLETON W J. Comments on "Generalized Box-Müller method for generating q-Gaussian random deviates"[J]. IEEE Transactions on Information Theory,2021,67(10):6785-6789. DOI: 10.1109/TIT.2021.3071489
[20]	谷晓忱,张民选. 一种基于FPGA的高斯随机数生成器的设计与实现[J]. 计算机学报,2011,34(1):165-173. DOI: 10.3724/SP.J.1016.2011.00165 GU Xiaochen,ZHANG Minxuan. Design and implementation of a FPGA based Gaussian random number generator[J]. Chinese Journal of Computers,2011,34(1):165-173. DOI: 10.3724/SP.J.1016.2011.00165
[21]	ARNAIZ-GONZÁLEZ Á,DÍEZ-PASTOR J-F,RODRÍGUEZ J J,et al. Instance selection of linear complexity for big data[J]. Knowledge-Based Systems,2016,107:83-95. DOI: 10.1016/j.knosys.2016.05.056

施引文献(14)

期刊类型引用(10)

1.	林广旭. 基于BP神经网络模型的带式输送机张紧力波动规律分析. 机电产品开发与创新. 2025(02): 121-124 . 百度学术
2.	林广旭. 煤矿用梭车运输电机设计与特性分析. 煤矿机械. 2025(05): 13-16 . 百度学术
3.	林广旭. JOY10SC32-48B梭车转载电动机国产化修复对比试验研究. 矿山机械. 2025(05): 9-13 . 百度学术
4.	吕杰. 神经网络在带式输送机张紧力控制系统中的应用与对比. 机械管理开发. 2023(07): 225-227 . 百度学术
5.	冯书文. 煤矿用带式输送机皮带张紧智能控制设计. 江西煤炭科技. 2022(02): 189-191 . 百度学术
6.	武进. 带式输送机皮带液压张紧控制系统分析. 山西焦煤科技. 2021(03): 21-23+50 . 百度学术
7.	刘媛媛. 煤矿机电设备智能化维护研究现状与发展趋势. 工矿自动化. 2021(07): 79-84 . 本站查看
8.	牛婷婷，李明，白晋铭. 基于RBF网络的带式输送机张紧力前馈控制. 煤矿机械. 2019(04): 167-169 . 百度学术
9.	樊治. 自动感应张紧装置在矿用带式输送机中的应用. 机械管理开发. 2019(06): 177-178 . 百度学术
10.	杨卫东. 带式输送机自动张紧装置. 装备制造技术. 2019(05): 130-134 . 百度学术