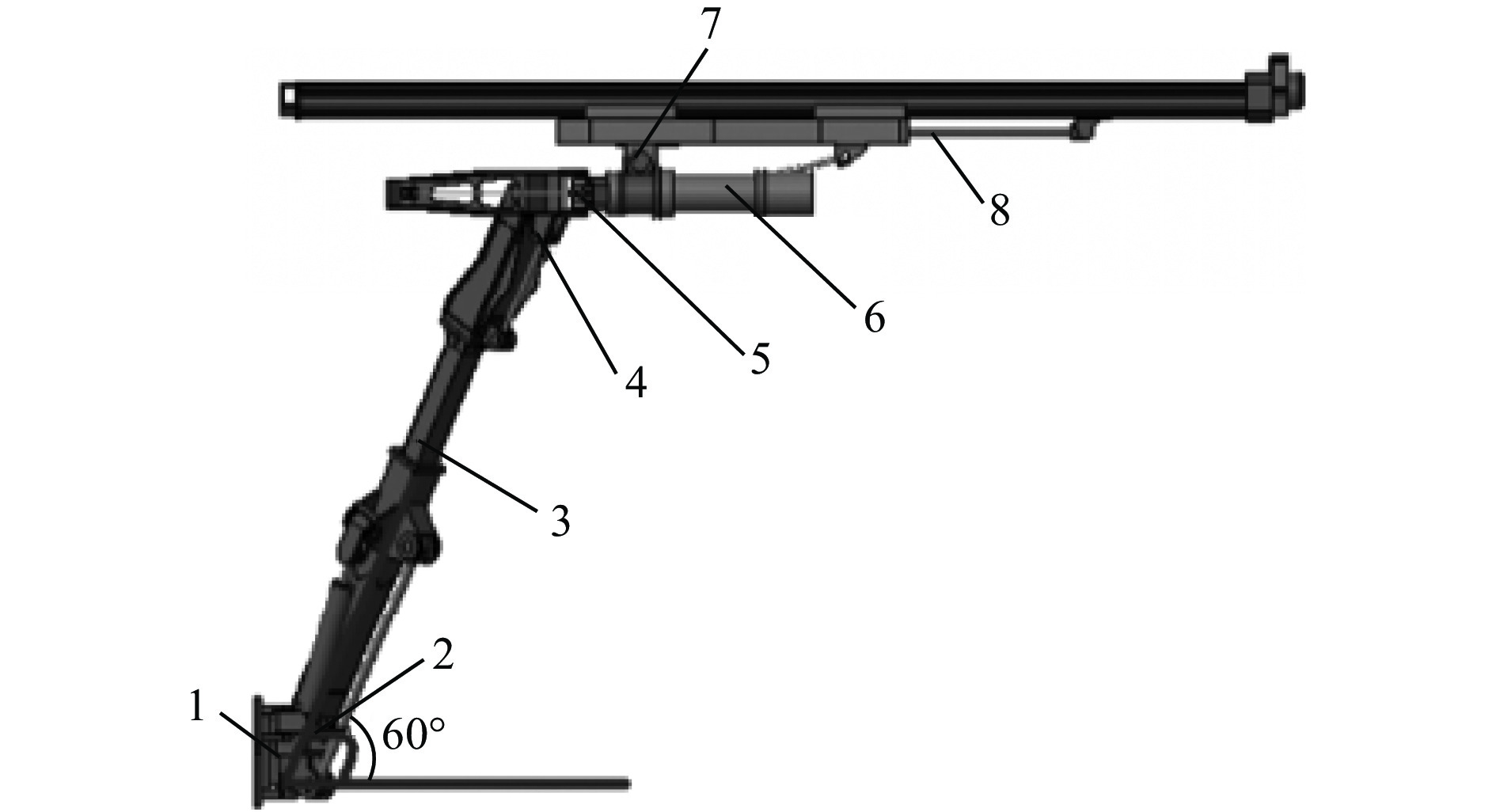
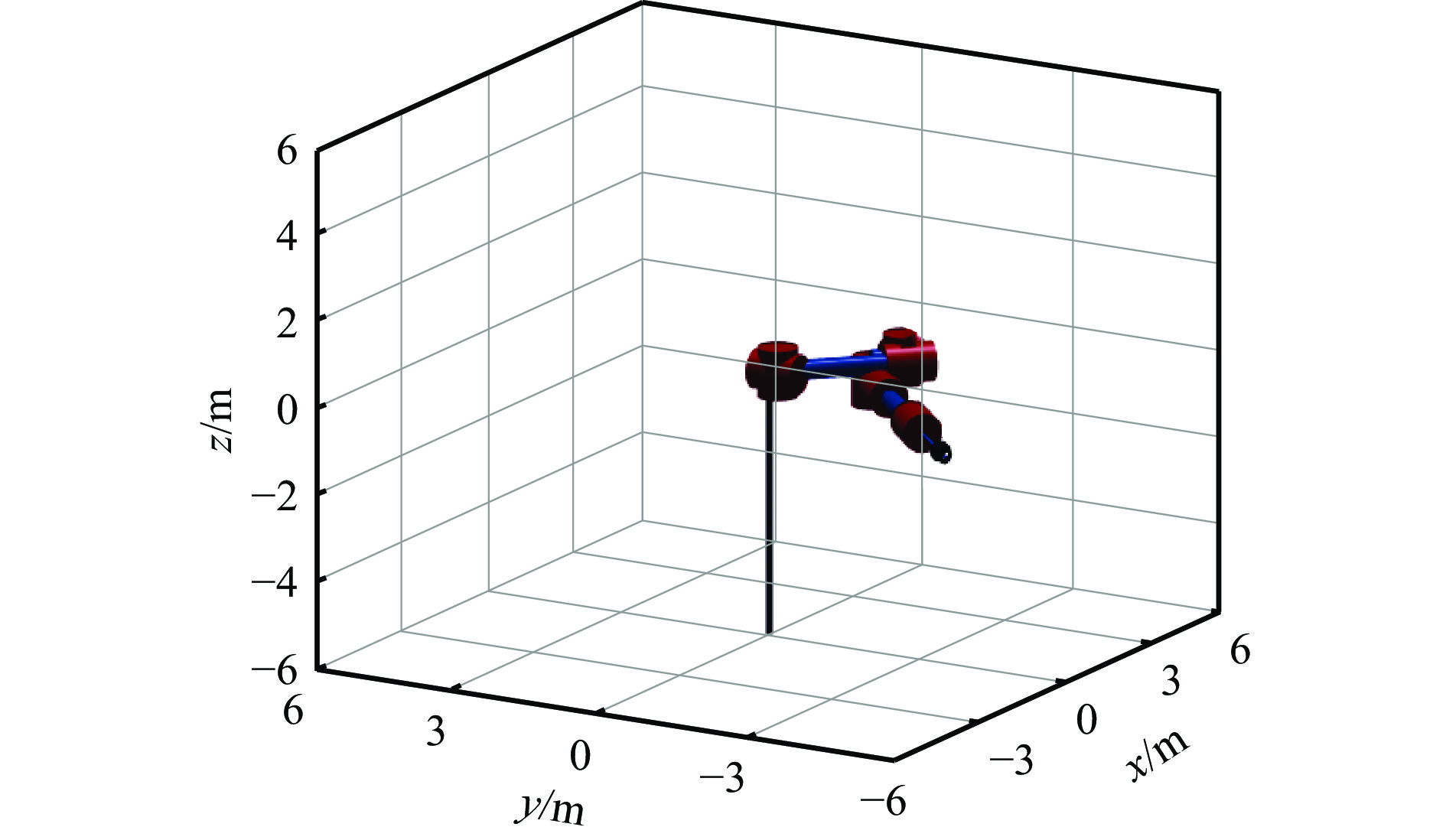
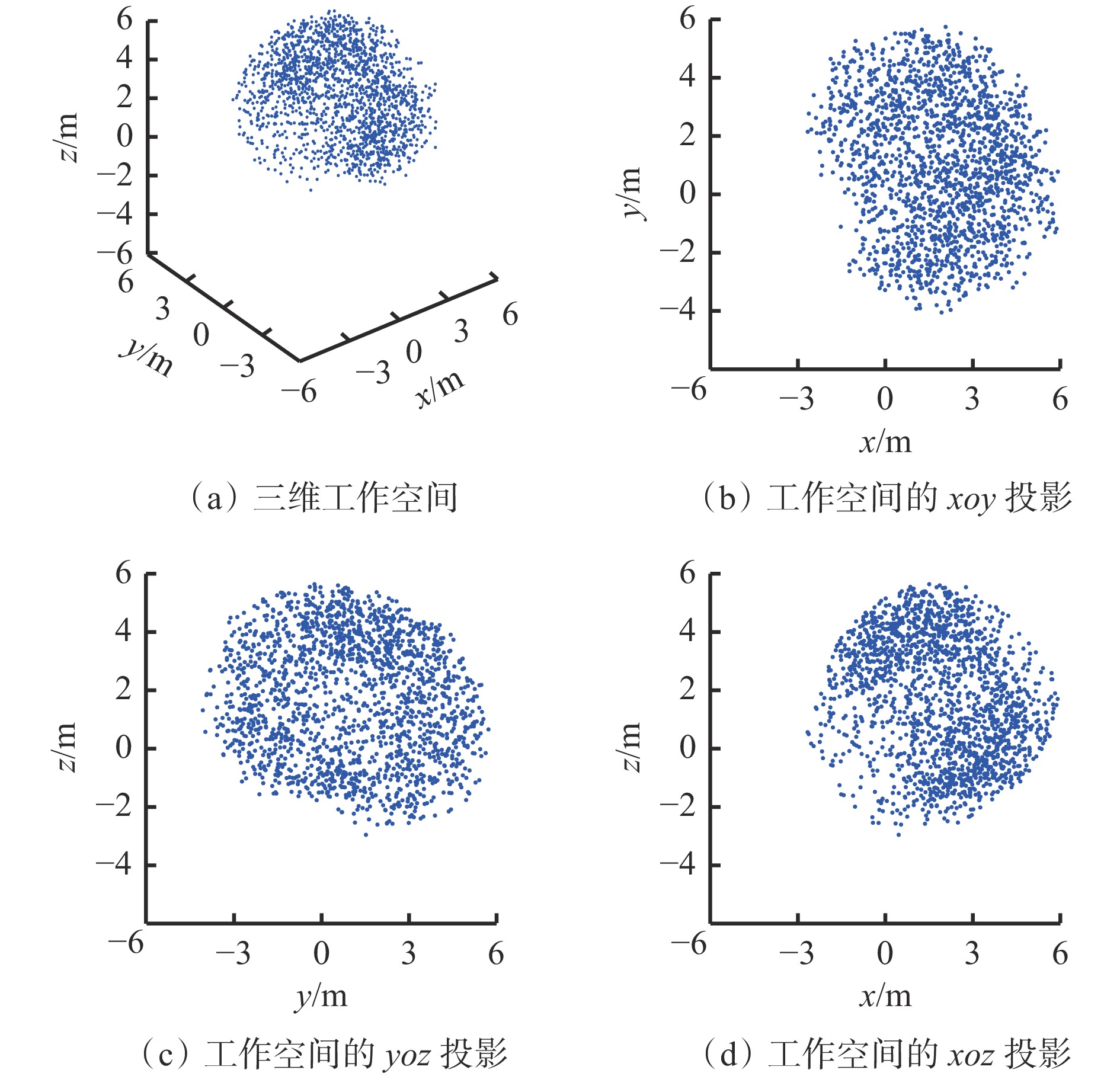
Positioning control method for drilling arm of bolt drilling rig
-
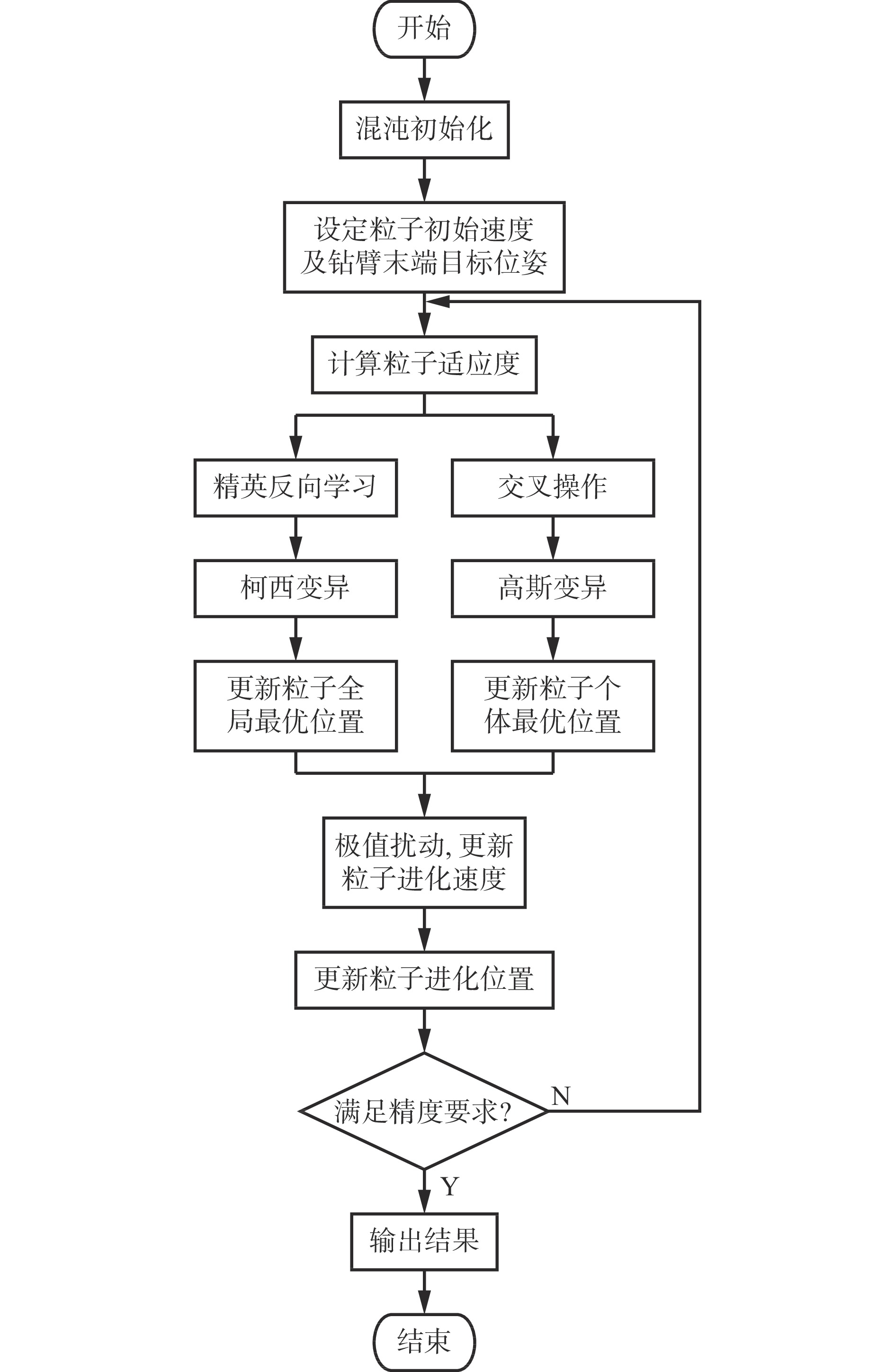
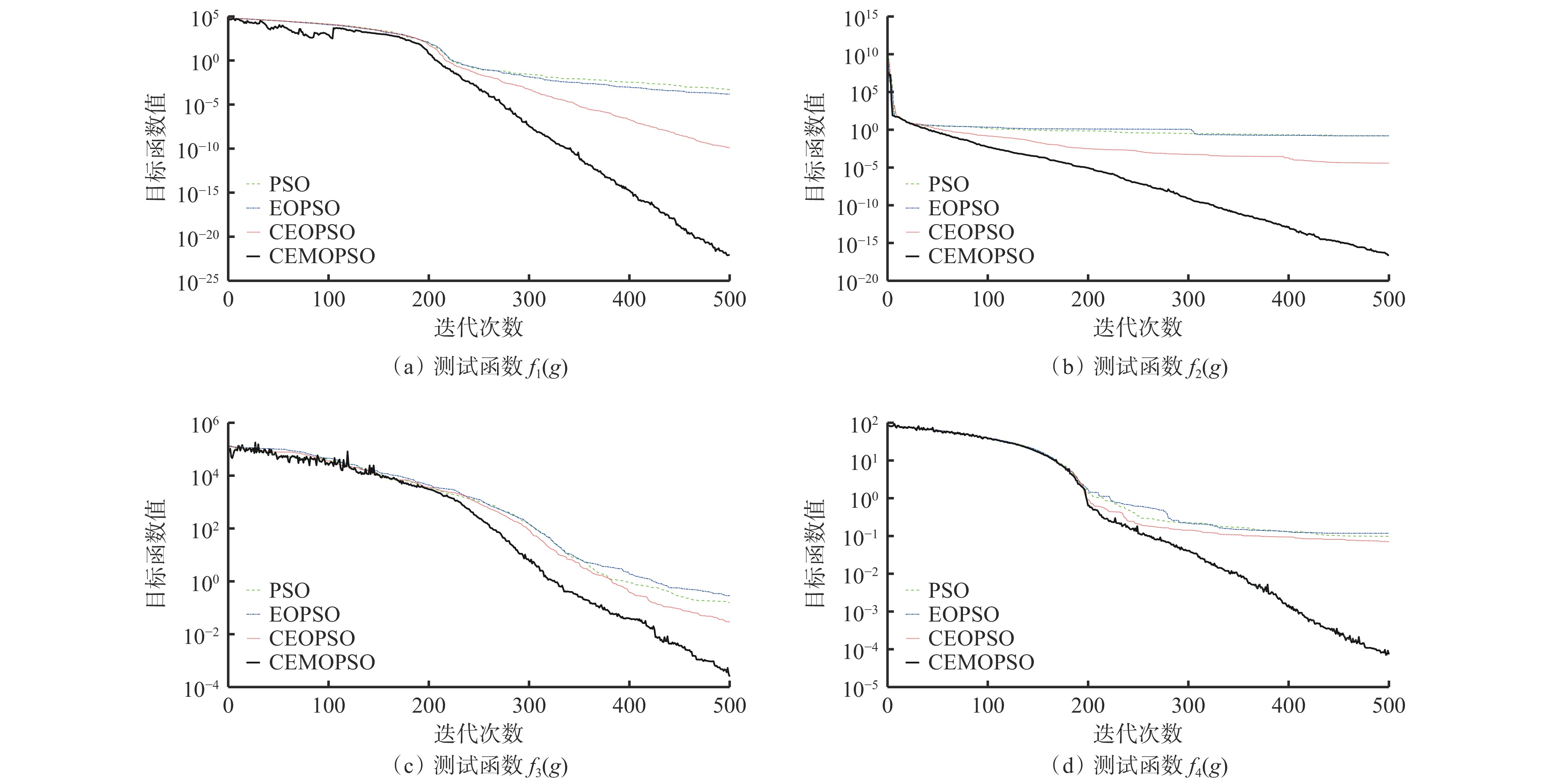
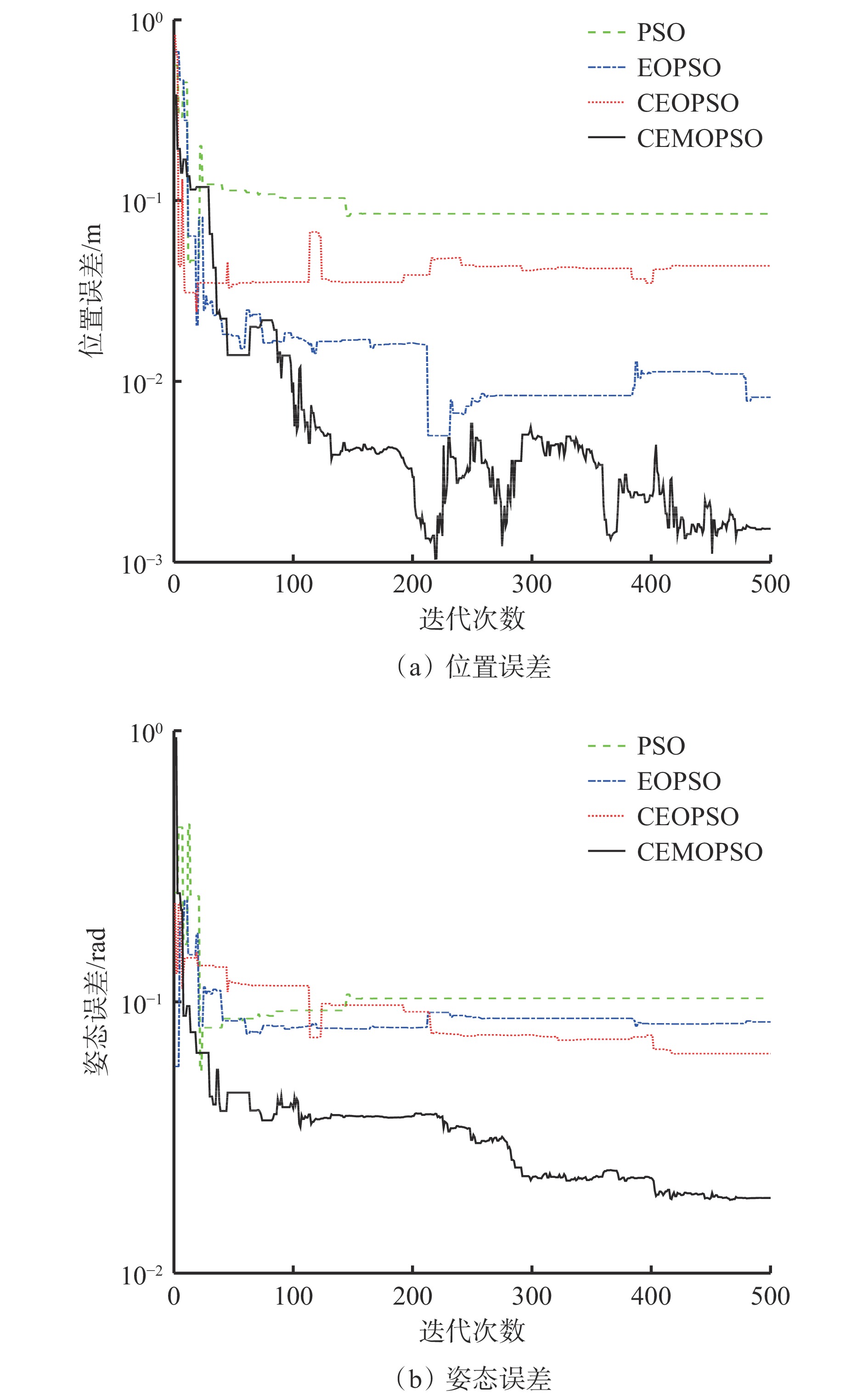
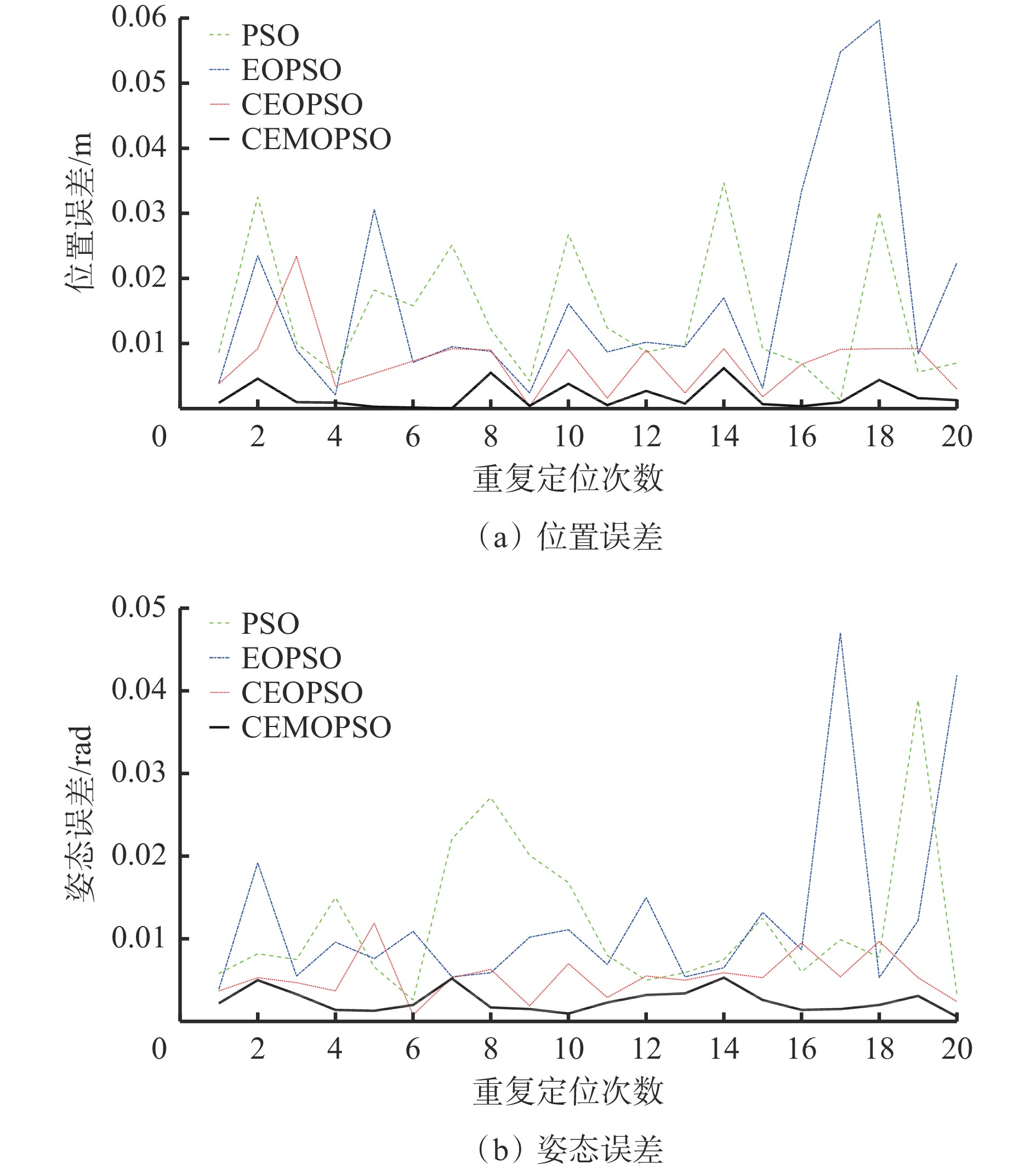
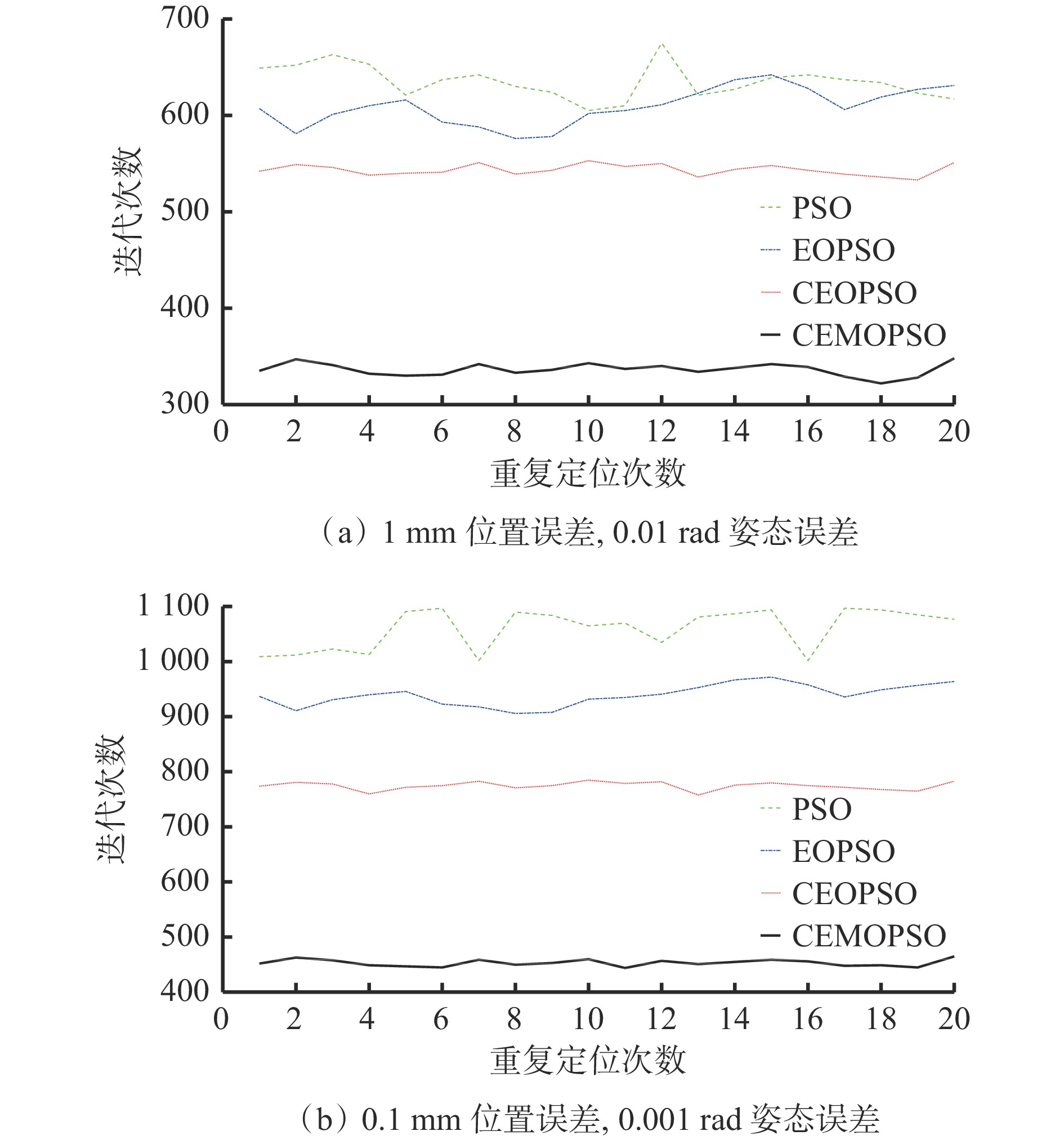
摘要: 目前常用代数法和几何法实现锚杆钻车钻臂定位控制，存在效率低、有无解或多解情况、通用性差等问题。采用粒子群优化（PSO）算法进行机械臂定位控制具有编程简单、搜索性能强、容错性好等优势，但易陷入局部最优解。目前基于改进PSO算法的机械臂定位控制整体寻优效率较低，寻优时间过长。针对上述问题，在精英反向粒子群优化（EOPSO）算法基础上，引入混沌初始化、交叉操作、变异操作和极值扰动，设计了混沌交叉精英变异反向粒子群优化(CEMOPSO）算法。采用标准测试函数对PSO算法、EOPSO算法、交叉精英反向粒子群优化（CEOPSO）算法、CEMOPSO算法进行测试，结果表明CEMOPSO算法的稳定性、精度、收敛速度最优。建立了锚杆钻车钻臂运动模型，采用CEMOPSO算法进行钻臂定位控制，并在Matlab软件中对控制性能进行仿真研究，结果表明：在相同的迭代次数和误差精度约束条件下，采用CEMOPSO算法时钻臂位置误差和姿态误差从迭代初期即具有极快的收敛速度，且位置误差和姿态误差均小于其他3种算法，误差曲线较平稳，最大位置误差为0.005 m，最大姿态误差为0.005 rad；设定位置误差为1 mm、姿态误差为0.01 rad时，CEMOPSO算法的平均迭代次数为343，位置误差为0.1 mm、姿态误差为0.001 rad时平均迭代次数为473，在相同的定位精度条件下，CEMOPSO算法的收敛速度和稳定性优于其他3种算法，满足工程应用要求，且求解精度越高，其优越性越突出。Abstract: Algebraic and geometric methods are commonly used to realize drilling arm positioning control of bolt drilling rig. However, there are some problems such as low efficiency, no solution, multiple solutions, or poor universality. Using particle swarm optimization (POS) algorithm for positioning control of the drilling arm has the advantages of simple programming, strong search performance and good fault tolerance. But it is easy to fall into the local optimal solution. At present, the drilling arm positioning control based on improved PSO algorithm has low overall optimization efficiency and long optimization time. In order to solve the above problems, a chaotic crossover elite mutation opposition-based PSO (CEMOPSO) algorithm is designed by introducing chaos initialization, crossover operation, mutation operation and extreme value perturbation based on elite opposition-based PSO (EOPOS) algorithm. The method uses standard test functions to test PSO algorithm, EOPSO algorithm, CEOPSO algorithm and CEMOPSO algorithm. The results show that CEMOPSO has the best stability, precision and convergence speed. The motion model of the drilling arm of the bolt drilling rig is established. The CEMOPSO algorithm is used to control the drilling arm positioning. The simulation of the control performance is carried out in Matlab. The results show that under the same iteration times and error precision constraints, the position error and posture error of the drilling arm have a very fast convergence rate from the initial iteration when using the CEMOPSO algorithm. The position error and posture error are smaller than those of the other three algorithms. The error curve is smooth, and the maximum position error is 0.005 m and the maximum posture error is 0.005 rad. When the position error is 1 mm and the posture error is 0.01 rad, the average iteration number of the CEMOPSO algorithm is 343. When the position error is 0.1 mm and the posture error is 0.001 rad, the average iteration number is 473. Under the same positioning precision, the convergence speed and stability of the CEMOPSO algorithm are better than those of the other three algorithms. The results meet the requirements of engineering application. The higher the accuracy of the solution, the better it is.
-
0. 引言
煤炭是我国国民经济的基础，在当前和未来相当长时期内，煤炭作为我国主体能源的地位不会改变，一次能源占比在50%以上，90%以上的煤炭以井工方式开采。“采掘并重，掘进先行”是煤炭开采的原则，综掘智能化落后于综采智能化，采掘失衡矛盾突出。据统计，我国年煤巷掘进量约为12 000 km，绝大多数采用悬臂式掘进机完成。我国煤矿掘进工作面存在智能化程度不高、用人多、环境差、事故多发等突出问题，智能掘进已成为国家和行业关注的热点和痛点，掘进关键装备的智能化是当前卡脖子的问题[1-2]。悬臂式掘进机绝对位姿的快速准确测量是实现煤矿巷道智能掘进的前提和基础。
悬臂式掘进机位姿测量方法主要有2类：一类是通过机载高精度传感器如捷联惯导[3]、加速度和超声波传感器的融合测量[4]等实现自主测量的方法，使用方便，但属于相对测量，测量精度较低或成本较高；另一类是利用外置式测量装置，如激光跟踪仪、全站仪[5]、激光导向仪、机器视觉、iGPS[6]、UWB[7]等，测量精度高，受杂波干扰小，但布置繁琐，测量范围有限，受环境影响大。目前，利用激光的悬臂式掘进机位姿测量方法因可靠性高、成本低、无误差累计等优点深受业内专家学者的关注。周玲玲等[8]利用2对激光指向仪和激光标靶构建了悬臂式掘进机位姿实时检测系统。吴淼等[9]提出了一种基于空间交汇测量技术的悬臂式掘进机位姿测量方法，利用激光装置得到了悬臂式掘进机位姿参数。马一心等[10]提出了多台激光跟踪仪联合动态位姿测量方法，可实现悬臂式掘进机位姿精度评定。邓国华[11]利用激光指向测距仪和光测角仪测量悬臂式掘进机相对于指向激光的方向角和俯仰角，但测量过程中需要调动掘进机使激光发射到光测角仪上。Li Jianguo等[12]利用激光装置研究了金属矿井下铲运车的位置参数测量方法。Du Yuxin等[13]利用视觉测量原理和双十字激光源照射在标靶上的图像，实现了悬臂式掘进机相对于巷道的姿态参数和偏移参数的测量。张超等[14]将红外LED光源组成图像测量标靶，人为构造图像特征来解决特征选取问题，实现了位姿参数求解。
综上可知，基于激光的悬臂式掘进机位姿测量方法存在非绝对位姿测量、测量精度较低、使用繁琐和测量参数单一等问题，且多处于理论研究阶段，尚不能满足智能掘进需要。为此，本文在已有研究基础上[15-16]，优化了基于激光靶向跟踪的悬臂式掘进机位姿测量方法，设计了基于激光靶向跟踪的悬臂式掘进机位姿测量系统，实现了悬臂式掘进机在巷道大地坐标系中绝对位姿的一次性全参数实时测量。仿真和实验分析了该系统的误差分布规律，为悬臂式掘进机在巷道大地坐标系绝对位姿的快速准确测量提供思路。
1. 系统组成与测量原理
1.1 系统组成
基于激光靶向跟踪的悬臂式掘进机位姿测量系统由激光跟踪装置和激光标靶组成，激光跟踪装置安装在后方巷道顶板处，激光标靶安装在掘进机机身上，如图1所示。
![]()
图 1 悬臂式掘进机位姿测量系统组成Figure 1. Composition of pose measurement system of cantilever roadheader悬臂式掘进机位姿测量系统结构与工作原理如图2所示。激光跟踪装置由激光测距模块、无线通信模块、处理器模块和二自由度云台等组成。激光标靶主要由激光靶面、倾角传感器、2个高分辨率相机、无线通信模块和机载工控机等组成，其中激光靶面由2个相互垂直的光学靶面组成，竖向靶面是一块半透半反射分光板，横向靶面是一块散射透光板。在无线通信模块引导下，激光跟踪装置的处理器模块控制二自由度云台俯仰或回转，使激光测距模块的激光束发射到激光标靶的竖向靶面目标区域并被反射至横向靶面上，在2个靶面上各形成一块光斑，并利用激光测距模块测得激光标靶和激光跟踪装置间的距离。激光标靶的相机1和相机2分别采集竖向靶面和横向靶面的光斑图像，输出至机载工控机，提取光斑中心坐标；激光标靶的无线通信模块将光斑中心坐标发送给激光跟踪装置，为其处理器模块控制二自由度云台提供信息，同时接收激光跟踪装置无线通信模块发来的测距值和二自由度云台的俯仰与偏向角度值，并传输给机载工控机；倾角传感器测出激光标靶的俯仰角并传输给机载工控机；机载工控机根据上述测量值解算出悬臂式掘进机绝对位姿。
![]()
图 2 悬臂式掘进机位姿测量系统结构与工作原理Figure 2. Structure and operation principle of pose measurement system of cantilever roadheader1.2 位姿测量原理
掘进机机身坐标系{S}以掘进机机身中心点OS为原点，XS轴沿掘进机机身中线指向巷道掘进方向，ZS轴垂直掘进机机身向上；激光跟踪坐标系{J}以激光跟踪装置的回转和俯仰中心点OJ为原点，激光发射方向为XJ轴正向，回转轴向上为ZJ轴正向；激光标靶坐标系{B}以激光标靶的竖向靶面与横向靶面交线右顶点OB为原点，沿交线向左为YB轴正向，沿竖向靶面向上为ZB轴正向；巷道大地坐标系{H}以巷道中大地坐标已知点OH为原点，XH轴沿巷道中线指向掘进方向，ZH轴垂直水平面向上。掘进机位姿测量就是要确定掘进机在巷道大地坐标系中的位姿，如图3所示。
![]()
图 3 悬臂式掘进机位姿测量系统坐标系及其转换关系Figure 3. Coordinate systems of pose measurement system of cantilever roadheader and their transform relationships设Jp为空间任一点
$p $ 在激光跟踪坐标系中的齐次坐标，Hp为点$p $ 在巷道大地坐标系中的齐次坐标，即$$\left\{\begin{aligned} &{}^{\text{J}}{{{\boldsymbol{p}}}} = \left[ {\begin{array}{*{20}{c}} {{}^{\text{J}}{p_x}} \\ {{}^{\text{J}}{p_y}} \\ {{}^{\text{J}}{p_z}} \\ 1 \end{array}} \right] \\ &{}^{\text{H}}{{{\boldsymbol{p}}}} = \left[ {\begin{array}{*{20}{c}} {{}^{\text{H}}{p_x}} \\ {{}^{\text{H}}{p_y}} \\ {{}^{\text{H}}{p_z}} \\ 1 \end{array}} \right] \end{aligned} \right. $$ (1) 式中：(Jpx, Jpy, Jpz)为点
$p $ 在激光跟踪坐标系中的坐标；(Hpx, Hpy, Hpz)为点$p $ 在巷道大地坐标系中的坐标。根据图3和式（1）有
$$ {}^{\text{H}}{{{\boldsymbol{p}}}} = {}_{\text{J}}^{\text{H}}{\boldsymbol{T}}{}^{\text{J}}{{{\boldsymbol{p}}}} $$ (2) 其中：
$$ \begin{gathered} {}_{\text{J}}^{\text{H}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos\;{\alpha _0}\cos\; {\beta _0}}&{ - \sin\; {\alpha _0}}&{ - \cos\; {\alpha _0}\sin \;{\beta _0}}&{{}^{\text{H}}{x_{{{\text{J}}_{\text{O}}}}}} \\ {\sin\; {\alpha _0}\cos\; {\beta _0}}&{\cos\; {\alpha _0}}&{ - \sin\; {\alpha _0}\sin\; {\beta _0}}&{{}^{\text{H}}{y_{{{\text{J}}_{\text{O}}}}}} \\ {\sin\; {\beta _0}}&0&{\cos\; {\beta _0}}&{{}^{\text{H}}{z_{{{\text{J}}_{\text{O}}}}}} \\ 0&0&0&1 \end{array}} \right] \\ \end{gathered} $$ (3) 式中：
${}_{\text{J}}^{\text{H}}{\boldsymbol{T}}$ 为巷道大地坐标系到激光跟踪坐标系的转换矩阵；α0，β0分别为激光跟踪坐标系沿巷道大地坐标系ZH轴和YH轴旋转的角度，即激光跟踪装置的偏向角和俯仰角，由激光跟踪装置的角度编码器测得；$ \left({}^{\text{H}}x{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}y{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}z{}_{{\text{J}}_{\text{O}}}\right) $ 为激光跟踪坐标系原点OJ在巷道大地坐标系中的坐标。同样地，激光标靶坐标系中任意一点
$q $ 的坐标记为${}^{{\rm{B}}}{\boldsymbol{q}} $ ，其在激光跟踪坐标系中的坐标记为${}^{{\rm{J}}}{\boldsymbol{q}} $ ，则有$$ {}^{\text{J}}{{{\boldsymbol{q}}}} = {}_{\text{B}}^{\text{J}}T{}^{\mathbf{B}}{{{\boldsymbol{q}}}} $$ (4) 式中
${}^{\rm{J}}_{\rm{B}}{\boldsymbol{T}}$ 为激光跟踪标系到激光标靶坐标系的转换矩阵。$$ {}_{\text{B}}^{\text{J}}{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos\; {\alpha _1}\cos\;{\beta _1}}&{ - \sin\; {\alpha _1}}&{ - \cos \;{\alpha _1}\sin \;{\beta _1}}&{{}^{\text{J}}{x_{{{\text{B}}_{\text{O}}}}}} \\ {\sin\; {\beta _1}\sin\;{\gamma _1} + \sin\; {\alpha _1}\cos\; {\beta _1}\cos\; {\gamma _1}}&{\cos\; {\alpha _1}\cos\; {\gamma _1}}&{\cos\; {\beta _1}{\text{sin}}\;{\gamma _1} - \sin\; {\alpha _1}\sin\; {\beta _1}\cos\; {\gamma _1}}&{{}^{\text{J}}{y_{{{\text{B}}_{\text{O}}}}}} \\ {\sin\; {\beta _1}\cos\; {\gamma _1} - \sin\; {\alpha _1}\cos\; {\beta _1}\sin \;{\gamma _1}}&{ - \cos\; {\alpha _1}\sin\; {\gamma _1}}&{\cos\; {\beta _1}\cos\; {\gamma _1} + \sin\; {\alpha _1}\sin \;{\beta _1}\sin\; {\gamma _1}}&{{}^{\text{J}}{z_{{{\text{B}}_{\text{O}}}}}} \\ 0&0&0&1 \end{array}} \right] $$ (5) 式中：α1，β1，γ1分别为激光标靶坐标系沿激光跟踪坐标系ZJ轴、YJ轴和XJ轴旋转的角度；
$ ({}^{\text{J}}x{}_{{\text{B}}_{\text{O}}}，{}^{\text{J}}y{}_{{\text{B}}_{\text{O}}}， {}^{\text{J}}z{}_{{\text{B}}_{\text{O}}}) $ 为激光标靶坐标系原点OB在激光跟踪坐标系中的坐标。测量时，激光跟踪装置发射一束激光照射到激光标靶的竖向靶面上，经竖向靶面反射后又照射到激光标靶的横向靶面上，在2个靶面上形成2块激光光斑，如图3中的点A和a。设点A在激光标靶坐标系中的坐标为(0, yA, zA)，在激光跟踪坐标系中的坐标为(d,0,0)，其中d为激光跟踪装置坐标原点OJ与点A之间的距离。点a在激光标靶坐标系中的坐标为(−xa, ya, 0)，点a关于YBOBZB平面的对称点为a′(xa, ya, 0)，该点在激光跟踪坐标系中的坐标为(dc,0,0)，其中dc为激光束到达竖向靶面经反射后到达横向靶面的距离，由激光跟踪装置中的激光测距模块测得。则有
$$ \left\{ \begin{gathered} {}^{\text{J}}{{{\boldsymbol{A}}}} = {}_{\text{B}}^{\text{J}}{\boldsymbol{T}\,} {}^{\text{B}} {{{\boldsymbol{A}}}} \\ {}^{\text{J}}{{{\boldsymbol{a}}}} = {}_{\text{B}}^{\text{J}}{\boldsymbol{T}\,} {}^{\text{B}} {{{\boldsymbol{a}}}} \\ {}^{\text{J}}{{{\boldsymbol{a}}'}} = {}_{\text{B}}^{\text{J}}{\boldsymbol{T}\,} {}^{\text{B}} {{{\boldsymbol{a}}'}} \\ \end{gathered} \right. $$ (6) $d = {d_{\text{c}}} - \sqrt {{{\left( {{y_{\text{A}}} - {y_{\text{a}}}} \right)}^2} + x_{\text{a}}^2 + \textit{z}_{\text{A}}^2}$ ，由此可求解得到$$\left\{\begin{array}{l} \alpha_{1}=\arctan \dfrac{y_{\mathrm{A}}-y_{{\rm{a}}}}{\sqrt{\textit{z}_{\mathrm{A}}^{2}+x_{{\rm{a}}}^{2}}} \\ \beta_{1}=-\arctan \dfrac{\textit{z}_{\mathrm{A}}}{x_{{\rm{a}}}} \end{array}\right.$$ (7) $$ \begin{split} \\ \left\{\begin{aligned} { }^{\mathrm{J}} x_{\mathrm{B}_{\mathrm{O}}}=& d+y_{\mathrm{A}} \sin\; \alpha_{1}+\textit{z}_{\mathrm{A}} \cos\; \alpha_{1} \sin\; \beta_{1} \\[-1pt] { }^{\mathrm{J}} y_{\mathrm{B}_{\mathrm{O}}}=& \textit{z}_{\mathrm{A}}\left(\sin\; \alpha_{1} \sin\; \beta_{1} \cos\; \gamma_{1}-\cos\; \beta_{1} \sin\; \gamma_{1}\right)- \\[-1pt] & y_{\mathrm{A}} \cos\; \alpha_{1} \cos\; \gamma_{1} \\[-1pt] { }^{\mathrm{J}} \textit{z}_{\mathrm{B}_{\mathrm{O}}}=& y_{\mathrm{A}} \cos\; \alpha_{1} \sin\; \gamma_{1} -\\[-1pt] & \textit{z}_{\mathrm{A}}\left(\sin\; \alpha_{1} \sin\; \beta_{1} \sin\; \gamma_{1}+\cos\; \beta_{1} \cos\; \gamma_{1}\right) \end{aligned}\right. \end{split}$$ (8) 为便于接收激光跟踪装置发射的激光，使激光标靶的2个正交靶面与水平面夹角呈45°，使用时激光标靶靶面开口应朝向巷道后方的激光跟踪装置。激光标靶底座上安装有倾角传感器，用于测量激光标靶与巷道大地坐标系水平面间的夹角γq，利用γq可计算得到γ1。
$$ {{\rm{\gamma}} _1} = {\text{arcsin}} \frac{{\sin\; {\gamma _{\text{q}}} - \sin\; {\alpha _1}\sin\; {\beta _0}}}{{\cos\; {\alpha _1}\cos\; {\beta _0}}} $$ (9) 设Sn为空间任意一点n在掘进机机身坐标系中的齐次坐标，Bn为点n在激光标靶坐标系中的齐次坐标，则有
$$ { }^{\mathrm{B}} {{\boldsymbol{n}}}={ }_{\mathrm{S}}^{\mathrm{B}} {\boldsymbol{T}\,}^{\mathrm{S}} {{\boldsymbol{n}}} $$ (10) 其中：
$$ \begin{gathered} {}_{\text{S}}^{\text{B}}{{{\boldsymbol{T}}}} = \left[ {\begin{array}{*{20}{c}} {\cos\; {\alpha _2}\cos\; {\beta _2}}& { - \sin\; {\alpha _2}}& { - \cos\; {\alpha _2}\sin\; {\beta _2}}& {{}^{\text{B}}{x_{{{\text{S}}_{\text{O}}}}}} \\ {\sin\; {\alpha _2}\cos\; {\beta _2}}& {\cos\; {\alpha _2}}& { - \sin\; {\alpha _2}\sin\; {\beta _2}}& {{}^{\text{B}}{y_{{{\text{S}}_{\text{O}}}}}} \\ {\sin\; {\beta _2}}& 0& {\cos\; {\beta _2}}& {{}^{\text{B}}{\textit{z}_{{{\text{S}}_{\text{O}}}}}} \\ 0& 0& 0& 1 \end{array}} \right] \end{gathered} $$ (11) 式中：
${}_{\rm{S}}^{\rm{B}} {\boldsymbol{T}} $ 为激光标靶坐标系到掘进机机身坐标系的转换矩阵；α2，β2，γ2分别为掘进机机身坐标系沿激光标靶坐标系ZB轴、YB轴和XB轴旋转的角度；$ \left({}^{\text{B}}x{}_{{\text{S}}_{\text{O}}}，\right. \left.{}^{\text{B}}y{}_{{\text{S}}_{\text{O}}}，{}^{\text{B}}\textit{z}{}_{{\text{S}}_{\text{O}}}\right) $ 为掘进机机身坐标系原点OS在激光标靶坐标系中的坐标。同时，设α，β，γ为掘进机在巷道大地坐标系中的偏向角、俯仰角和翻滚角，(x, y, z)为掘进机在巷道大地坐标系中的位置坐标，对应掘进方向位置、偏距和高度，则掘进机机身坐标系到巷道大地坐标系的转换矩阵为
$$ {}_{\text{S}}^{\text{H}}{{{\boldsymbol{T}}}} = \left[ {\begin{array}{*{20}{c}} {\cos\; \alpha \cos\; \beta }&{ - \sin\; \alpha }&{ - \cos\; \alpha \sin\; \beta }&x \\ {\sin\; \beta \sin\; \gamma + \sin\; \alpha \cos\; \beta \cos\; \gamma }&{\cos\; \alpha \cos\; \gamma }&{\cos\; \beta \sin\; \gamma - \sin\; \alpha \sin\; \beta \cos\; \gamma }&y \\ {\sin\; \beta \cos\; \gamma - \sin\; \alpha \cos\; \beta \sin\; \gamma }&{ - \cos\; \alpha \sin\; \gamma }&{\cos\; \beta \cos\; \gamma + \sin\; \alpha \sin\; \beta \sin\; \gamma }&z \\ 0&0&0&1 \end{array}} \right] $$ (12) 由图3（b）所示的坐标转换关系可知：
$$ {}_{\text{S}}^{\text{H}}{\boldsymbol{T}} = {}_{\text{J}}^{\text{H}}{\boldsymbol{T}}\;\;{}_{\text{B}}^{\text{J}}{\boldsymbol{T}}\;\;{}_{\text{S}}^{\text{B}}{\boldsymbol{T}} $$ (13) 将式（3）、式（5）、式（11）和式（12）代入式（13），并利用等式两边矩阵对应元素相等建立方程组，可解得掘进机在巷道大地坐标系中的绝对位姿，即掘进机位姿测量数学模型：
$$ \left\{ {\begin{array}{*{20}{l}} {\alpha = - \arcsin {}_{\text{S}}^{\text{H}}{T_{12}}} \\ {\beta = - \arctan \dfrac{{{}_{\text{S}}^{\text{H}}{T_{13}}}}{{{}_{\text{S}}^{\text{H}}{T_{11}}}}} \\ {\gamma = - \arctan \dfrac{{{}_{\text{S}}^{\text{H}}{T_{32}}}}{{{}_{\text{S}}^{\text{H}}{T_{22}}}}} \\ {x = {}_{\text{S}}^{\text{H}}{T_{14}}} \\ {y = {}_{\text{S}}^{\text{H}}{T_{24}}} \\ {\textit{z} = {}_{\text{S}}^{\text{H}}{T_{34}}} \end{array} } \right. $$ (14) 式中
${}^{\rm{H}}_{\rm{S}}{{T}}_{ij}$ 为矩阵${}^{\rm{H}}_{\rm{S}}{\boldsymbol{T}} $ 第i行第j列元素。综上可知，悬臂式掘进机位姿测量与解算流程如下：
（1） 将激光标靶安装在掘进机机身上，并通过标定获得掘进机机身坐标系到激光标靶坐标系的转换矩阵
${}^{\rm{B}}_{\rm{S}}{\boldsymbol{T}}$ 。（2） 将激光跟踪装置安装在巷道某位置，标定获得其在巷道大地坐标系中的位置
$\left({}^{\text{H}}x{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}y{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}{\textit{z}}{}_{{\text{J}}_{\text{O}}}\right)$ 。（3） 激光跟踪装置根据无线模块接收的信息，控制二自由度云台运动，使发射的激光束照射到激光标靶的竖向靶面上，利用此时的偏向角α0和俯仰角β0，结合步骤（2）得到的坐标
$ \left({}^{\text{H}}x{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}y{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}{\textit{z}}{}_{{\text{J}}_{\text{O}}}\right) $ ，利用式（3）求得巷道大地坐标系到激光跟踪坐标系的转换矩阵${}^{\rm{H}}_{\rm{J}}{\boldsymbol{T}} $ 。同时，激光测距模块测得激光跟踪装置到激光标靶的距离dc。（4） 利用相机1和相机2分别获取竖向和横向靶面上激光光斑的坐标(0, yA, zA)和(−xa, ya, 0)，结合激光标靶内部倾角传感器测得的夹角γq，代入式（7）—式（9）和式（5），获得激光跟踪坐标系到激光标靶坐标系的转换矩阵
${}^{\rm{J}}_{\rm{B}}{\boldsymbol{T}}$ 。（5） 将
${}^{\rm{B}}_{\rm{S}}{\boldsymbol{T}} $ 、${}^{\rm{H}}_{\rm{J}}{\boldsymbol{T}}$ 、${}^{\rm{J}}_{\rm{B}}{\boldsymbol{T}}$ 代入式（13），获得掘进机机身坐标系到巷道大地坐标系的转换矩阵${}^{\rm{H}}_{\rm{S}}{\boldsymbol{T}} $ 。（6） 利用式（14）解算出掘进机在巷道大地坐标系中的绝对位置(x, y, z)和姿态（α, β, γ）。
（7） 重复步骤（3）—步骤（6），可连续测量得到掘进机在巷道大地坐标系中的绝对位姿。
（8） 当超出测量范围时，将激光跟踪装置前移，然后重复步骤（2）—步骤（7），即可实现悬臂式掘进机在巷道掘进过程中的绝对位姿测量。
2. 位姿测量误差仿真分析
根据建立的悬臂式掘进机位姿测量数学模型，分析悬臂式掘进机位姿测量系统中影响位姿解算精度的因素及位姿测量误差，确定系统各组成部分的结构尺寸和技术参数，建立系统仿真模型，分析掘进距离及激光跟踪装置安装位置对系统测量误差的影响规律，为系统现场应用和后续改进提供理论依据和数据参考。
2.1 精度影响因素
由悬臂式掘进机位姿测量数学模型可知，掘进机位姿参数解算与激光跟踪装置到激光标靶的距离、提取的激光光斑中心坐标、激光标靶倾角测量值、激光跟踪装置俯仰角与偏向角测量值有关，这些参数的测量误差均会影响掘进机位姿解算精度。
（1） 光斑中心坐标提取误差。现有的光斑视觉定位精度可达到像素级[17]，设计竖向、横向靶面的宽度均为 200 mm、高度均为 225 mm，以相机像素为960 dpi为例，每个像素点代表的实际尺寸为0.23 mm，考虑相机畸变标定后的残余误差，将激光标靶光斑中心坐标提取精度设为1 mm。
（2） 激光跟踪装置角度定位误差。激光跟踪装置偏向角和俯仰角跟踪的执行机构采用直流无刷伺服电动机，其定位误差与所用编码器精度有关。系统中选用的编码器为16 位，精度为0.005°。
（3） 激光测距误差。系统中采用SK80激光测距模块，最大测量范围为80 m，测量精度为2 mm。
（4） 激光标靶倾角测量误差。采用的倾角传感器分辨力为0.001°，全量程线性精度为0.005°。
2.2 仿真结果
合理设计系统各装置尺寸对其工程应用具有重要意义。掘进机位姿测量时，激光标靶安装在掘进机机身上，外形尺寸过大不利于测量的灵活性和安装的便利性，过小则不能满足测量范围要求。以EBZ220型掘进机为例，按掘进方向测量范围为5~80 m计算，偏向角α的变化范围为−27.7 ~ 42.6°，要满足上述要求会使激光标靶的尺寸非常大，不利于其安装使用。本文系统设计的激光标靶尺寸为225 mm×200 mm（高×宽），在5~80 m范围内其偏向角α测量范围为−16.25~+16.25°。为满足测量要求，需要对激光跟踪装置和激光标靶的安装位置进行分析。激光标靶的较佳安装位置：将底座安装在掘进机机身上，使激光标靶坐标系的XB轴与掘进机机身坐标系的XS轴呈45°夹角，YB轴与YS轴平行。假定激光跟踪装置安装在激光标靶正后方（标靶正后）、巷道左帮顶板处（顶部左帮）、巷道右帮顶板处（顶部右帮）、激光标靶正后方顶板处（顶部正后）、与激光标靶同一水平面巷道左帮处（标靶左帮）和与激光标靶同一水平面巷道右帮处（标靶右帮）6个位置。由于光斑中心坐标提取误差服从正态分布[18]，而倾角传感器和激光测距模块经过修正后误差可忽略不计，其随机误差也服从正态分布，假定光斑中心坐标提取误差、倾角传感器和激光测距模块的测量误差分布分别为正态分布N（500，2）、N（500，1）和N（500，1），为分析在5~80 m测量范围内掘进机位姿误差分布规律，每次均加入随机误差源分别对6个位置进行1 000次仿真解算，取误差最大值作为掘进机位姿测量误差。在5~80 m测量范围内每隔5 m进行1次仿真，结果如图4所示。
![]()
图 4 悬臂式掘进机位姿测量误差仿真曲线Figure 4. The error simulation curves of pose measurement of cantilever roadheader由图4可知，在5~80 m测量范围内，掘进机位姿测量误差呈现出以下规律：
（1） 偏向角误差小于1.30°，俯仰角误差小于1°，翻滚角误差小于0.03°；掘进方向位置误差小于5 mm，偏距和高度误差小于20 mm。
（2） 随着掘进距离增加，掘进机姿态误差均在一定范围内变化，且偏向角呈收敛趋势；偏距和高度误差随掘进距离增加呈线性增加趋势，但掘进方向位置误差不随掘进距离增加而增加。
（3） 激光跟踪装置安装位置对掘进机位姿测量误差有一定影响，标靶正后、标靶左帮和标靶右帮误差相对较小，其次为顶部正后，再次为顶部左帮和顶部右帮。激光跟踪装置安装位置为标靶正后、标靶左帮和标靶右帮时，偏向角误差小于1°，俯仰角误差小于0.7°，翻滚角误差小于0.03°，掘进方向位置误差小于5 mm，偏距和高度误差小于20 mm。激光跟踪装置安装在顶部左帮和顶部右帮时，偏向角误差小于1.30°，俯仰角误差小于0.90°，翻滚角误差小于0.03°，掘进方向位置误差小于5 mm，偏距和高度误差小于20 mm。激光跟踪装置安装在巷道顶部正后时，偏向角误差小于1.30°，俯仰角误差小于0.85°，翻滚角误差小于0.03°，掘进方向位置误差小于5 mm，偏距和高度误差小于20 mm。考虑到煤矿掘进工作面实际工况和遮挡问题，激光跟踪装置不宜安装在巷道两帮或中间较低位置，在允许情况下尽可能提高激光标靶安装高度。
3. 实验与结果分析
3.1 实验系统搭建
以履带式机器人底盘模拟掘进机机身，以楼道长走廊环境模拟煤矿巷道，将激光标靶安装在履带式机器人底盘上，激光跟踪装置放置在三脚架上，搭建掘进机位姿测量实验系统，如图5所示。履带式机器人机身坐标系原点OS在激光标靶坐标系中的位置坐标
$ \left({}^{\text{B}}x{}_{{\text{S}}_{\text{O}}}，{}^{\text{B}}y{}_{{\text{S}}_{\text{O}}}，{}^{\text{B}}{\textit{z}}{}_{{\text{S}}_{\text{O}}}\right) $ 标定结果为（−400，200，−230），掘进机机身坐标系在激光标靶坐标系中的偏向角α2为0，俯仰角β2为−45°。α0和β0分别为激光发射与激光测距模块的偏向角和俯仰角，$ \left({}^{\text{H}}x{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}y{}_{{\text{J}}_{\text{O}}}，{}^{\text{H}}{\textit{z}}{}_{{\text{J}}_{\text{O}}}\right) $ 为激光跟踪坐标系原点OJ在巷道大地坐标系中的位置参数，标定为（0,0,900）。![]()
图 5 悬臂式掘进机位姿测量实验系统Figure 5. Experimental system for pose measurement of cantilever roadheader3.2 实验结果
利用全站仪标定出履带式机器人在模拟巷道中的位姿，再利用搭建的实验系统测量掘进机位姿。测量过程中，微调激光跟踪装置的姿态角，使激光束入射到激光标靶竖向靶面的不同位置，以观察激光跟踪装置测量激光标靶的位姿精度变化情况。为了避免实验误差，进行了10组不同位姿参数的测量实验。第1—6组实验中履带式机器人在巷道大地坐标系下的位姿参数：x=4510.0 mm，y=−328.0 mm，z=368.0 mm，α=−2.000°，β=0.500°，γ=0.001°。第7—10组实验中履带式机器人在巷道大地坐标系下的位姿参数：x=5820.0 mm，y=196.0 mm，z=435.0 mm，α=−2.500°，β=1.000°，γ=0.001°。实验结果见表1。
表 1 实验结果Table 1. The experimental results序号 x/mm y/mm z/mm α/（°） β/（°） γ/（°） 测量值 误差 测量值 误差 测量值 误差 测量值 误差 测量值 误差 测量值 误差 1 4506.0 −4.0 −325.3 2.7 367.1 −0.9 −2.413 −0.413 0.323 −0.177 0.001 0 2 4507.4 −2.6 −326.7 1.3 367.7 −0.3 −2.078 −0.078 0.338 −0.162 0.001 0 3 4510.6 0.6 −328.2 −0.2 368.2 0.2 −1.637 0.363 0.532 0.032 0.001 0 4 4511.1 1.1 −328.7 −0.7 367.8 −0.2 −1.391 0.609 0.679 0.179 0.001 0 5 4509.1 −0.9 −328.6 −0.6 368 0 −1.622 0.378 0.436 −0.064 0.001 0 6 4509.1 −0.9 −328.9 −0.9 368.3 0.3 −1.815 0.185 0.301 −0.199 0.001 0 7 5817.2 −2.8 198.8 2.8 435.1 0.1 −2.711 −0.211 0.441 −0.559 0 −0.001 8 5822.6 2.6 199.0 3.0 436.4 1.4 −2.284 0.216 0.801 −0.199 0 −0.001 9 5822.0 2.0 196.9 0.9 435.6 0.6 −2.631 −0.131 1.217 0.217 0 −0.001 10 5824.3 4.3 197.3 1.3 435.3 0.3 −2.863 −0.363 1.184 0.184 0 −0.001 根据表1，绘制掘进机位置误差和姿态误差曲线，如图6所示。由图6可知，掘进方向位置x、偏距y和高度z测量绝对误差均小于5 mm，偏向角α测量绝对误差小于1°，俯仰角β测量绝对误差小于0.6°，翻滚角γ测量绝对误差可忽略不计，实验结果优于仿真结果。
3.3 讨论
定向掘进及断面自动截割成形是煤矿巷道智能掘进的题中之义。定向掘进的要义是控制好掘进巷道的中线和腰线。巷道中线控制需要知道掘进机的偏向角和偏距，而巷道腰线控制需要准确测量掘进机在巷道大地坐标系中的俯仰角和高度。仿真和实验结果均表明，本文系统偏向角测量误差较大，偏距和高度随掘进距离增加呈线性增加趋势。随着掘进距离增加，为保证掘进机偏距和高度的测量精度，需要将激光跟踪装置前移，自主快速标定其在巷道大地坐标系中的位姿。另外，煤矿井下环境复杂，粉尘大，照明不足，系统的有效性和环境适应性需要在现场环境下检验。因此，下一步应重点研究掘进机偏向角测量精度的改进措施、移站后自主快速标定技术和环境适应性等。
4. 结论
（1） 基于激光靶向跟踪的悬臂式掘进机位姿测量系统主要由激光跟踪装置和激光标靶组成。激光跟踪装置发射激光到激光标靶并在其2个靶面上形成光斑，且保持激光跟踪。激光标靶接收激光跟踪装置发射的激光束，根据2个靶面上的光斑位置和激光测距模块的测距信息，依据巷道大地坐标系、激光跟踪装置坐标系、激光标靶坐标系和掘进机机身坐标系之间的转换关系求解掘进机在巷道中的绝对位姿，实现了悬臂式掘进机在巷道坐标系中绝对位姿的全参数实时测量。
（2） 建立了悬臂式掘进机位姿测量数学模型，分析了系统的误差影响因素，仿真研究了系统的位姿测量误差分布规律，结果表明，该系统能够满足掘进机位姿检测精度要求，为工程应用提供支撑。
（3） 搭建了位姿测量实验系统，开展了其在模拟巷道中的位姿测量实验，分析了系统的测量精度，结果表明，掘进方向位置、偏距和高度测量绝对误差均小于5 mm，偏向角测量绝对误差小于1°，俯仰角测量绝对误差小于0.6°，翻滚角测量绝对误差可忽略不计，实验结果优于仿真结果。
（4） 煤矿井下粉尘大，照明条件差，悬臂式掘进机位姿测量系统的环境适应性还需后续现场实验验证。仿真和实验研究表明，掘进机偏向角测量误差稍大，为保障测量结果满足工程需要，系统测量范围有限，提高偏向角测量精度及移站后的自主标定是下一步研究重点。
-
![]()
图 1 锚杆钻车钻臂结构
1−大臂摇摆关节；2−大臂俯仰关节；3−大臂伸缩关节；4−推进梁俯仰关节；5−推进梁摆动关节；6−推进梁回转关节；7−锚杆关节；8−推进梁伸缩关节。
Figure 1. Drilling arm structure of bolt drilling rig
![]()
图 3 基于CEMOPSO算法的锚杆钻车钻臂定位控制流程
Figure 3. Positioning control flow of drilling arm of bolt drilling rig based on chaotic crossover elite mutation opposition-based particle swarm optimization(CEMOPSO) algorithm
![]()
图 7 4种算法对钻臂定位控制的位置误差和姿态误差收敛曲线
Figure 7. Convergence curves of position errors and posture errors of drilling arm positioning control by use of four algorithms
![]()
图 8 4种算法对钻臂定位控制的位置误差和姿态误差曲线
Figure 8. Position error and posture error curves of drilling arm positioning control by use of four algorithms
![]()
图 9 4种算法在不同精度条件下的迭代次数
Figure 9. Iteration times of four algorithms under different precision conditions
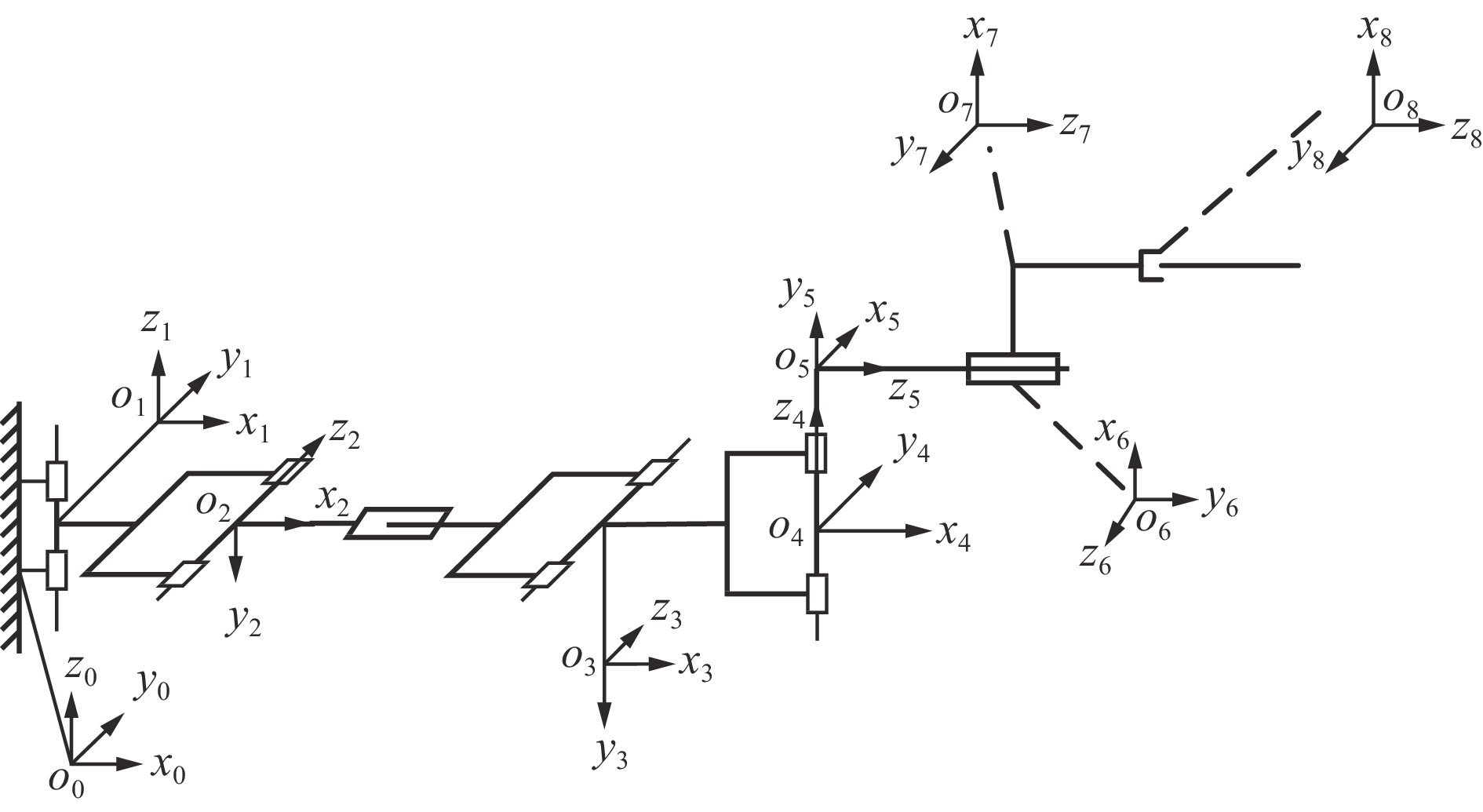
表 1 锚杆钻车钻臂D−H参数
Table 1 D-H parameters of drilling arm of bolt drilling rig
关节 $ {\theta _j}/(^\circ ) $ $ {\alpha _j}/(^\circ ) $ $ {a_j}/{\rm{m}} $ $ {d_j}/{\rm{m}} $ 1 [45，135] 90 0.30 0 2 [−150，−60] −90 0 0 3 180 −90 0 [0，1.8] 4 [−120，−30] −90 0.35 0 5 [−135，−45] 90 0 0 6 [−270，90] −90 0.60 0.4 7 [−90，0] 90 0 0.8 8 90 −90 0 [0，2.5] 
下载: 导出CSV
表 2 标准测试函数
Table 2 Standard test functions
函数 维度 搜索范围 最优解 ${f}_{1}(g)\text{=}{\displaystyle \sum _{r=1}^{n}{g}_{r}^{2} }$ 30 [−100，100] 0 ${f_2}(g) =\displaystyle \sum\limits_{r = 1}^n {\left| { {g_r} } \right|} + \prod\limits_{r = 1}^n {\left| { {g_r} } \right|}$ 30 [−10，10] 0 ${f_3}(g) = \displaystyle \sum\limits_{r = 1}^n {(\sum\limits_{q = 1}^n { {g_q}{)^2} } }$ 30 [−100，100] 0 $\mathop f\nolimits_4 (g) = \max \{ \left| {\mathop g\nolimits_r } \right|,1 \leqslant r \leqslant n\}$ 30 [−100，100] 0
下载: 导出CSV
表 3 标准测试函数计算结果
Table 3 Calculation results of standard test functions
函数 PSO算法 EOPSO算法 CEOPSO算法 CEMOPSO算法 $ {f_1}(g) $ 标准差：$3.223\; 2 \times {10^{ { { - } }2} }$ 标准差：$ 6.193\;9 \times {10^{{{ - }}2}} $ 标准差：$2.925\;9 \times {10^{{{ - 6}}}}$ 标准差：$2.870\;6 \times {10^{{{ - 18}}}}$ 最优解：$ 2.807\;2 \times {10^{{{ - }}2}} $ 最优解：$ 2.979\;5 \times {10^{{{ - }}2}} $ 最优解：$1.393\;2 \times {10^{{{ - 6}}}}$ 最优解：$4.794\;3 \times {10^{{{ - 19}}}}$ $ {f_2}(g) $ 标准差：$ 1.001\;8 \times {10^0} $ 标准差：$ 1.255\;4 \times {10^0} $ 标准差：$ 7.436\;1 \times {10^{{{ - }}2}} $ 标准差：$5.045\;2 \times {10^{{{ - 13}}}}$ 最优解：$ 8.349\;6 \times {10^{{{ - }}1}} $ 最优解：$ 8.012\;2 \times {10^{{{ - }}1}} $ 最优解：$ 6.558\;2 \times {10^{{{ - }}2}} $ 最优解：$1.479\;4 \times {10^{{{ - 13}}}}$ $ {f_3}(g) $ 标准差：$ 39.100\;3 \times {10^0} $ 标准差：$ 36.417\;4 \times {10^0} $ 标准差：$ 34.092\;9 \times {10^0} $ 标准差：$9.092\;9 \times {10^{{{ - }}2}}$ 最优解：$ 32.092\;9 \times {10^0} $ 最优解：$ 31.565\;9 \times {10^0} $ 最优解：$ 32.073\;7 \times {10^0} $ 最优解：$7.686\;5 \times {10^{{{ - }}2}}$ $ {f_4}(g) $ 标准差：$ 1.268\;5 \times {10^0} $ 标准差：$ 1.820\;8 \times {10^0} $ 标准差：$ 5.433\;3 \times {10^{{{ - }}1}} $ 标准差：$1.683\;6 \times {10^{{{ - 3}}}}$ 最优解：$ 1.167\;1 \times {10^0} $ 最优解：$ 1.035\;9 \times {10^0} $ 最优解：$ 5.398\;9 \times {10^{{{ - }}1}} $ 最优解：$1.327\;9 \times {10^{{{ - 3}}}}$
下载: 导出CSV
-
[1] 李国江,张飞,李露,等. 基于多种群协同进化算法的绳索牵引并联机器人末端位置误差补偿[J]. 机器人,2021,43(1):81-89. DOI: 10.13973/j.cnki.robot.200054 LI Guojiang,ZHANG Fei,LI Lu,et al. Error compensation of end-effector position for the cable-driven parallel robot based on multi-group co-evolutionary algorithm[J]. Robot,2021,43(1):81-89. DOI: 10.13973/j.cnki.robot.200054
[2] 吉阳珍,侯力,罗岚,等. 基于组合优化算法的6R机器人逆运动学求解[J]. 中国机械工程,2021,32(10):1222-1232. DOI: 10.3969/j.issn.1004-132X.2021.10.011 JI Yangzhen,HOU Li,LUO Lan,et al. Solution of inverse kinematics for 6R robots based on combinatorial optimization algorithm[J]. China Mechanical Engineering,2021,32(10):1222-1232. DOI: 10.3969/j.issn.1004-132X.2021.10.011
[3] 史也,梁斌,王学谦,等. 基于量子粒子群优化算法的空间机器人非完整笛卡尔路径规划[J]. 机械工程学报,2011,47(23):65-73. DOI: 10.3901/JME.2011.23.065 SHI Ye,LIANG Bin,WANG Xueqian,et al. Cartesian non-holonomic path planning of space robot based on quantum-behaved particle swarm optimization algorithm[J]. Journal of Mechanical Engineering,2011,47(23):65-73. DOI: 10.3901/JME.2011.23.065
[4] 刘洋. 基于多目标粒子群算法的机器人逆运动学求解方法[J]. 现代计算机,2020(10):13-17. DOI: 10.3969/j.issn.1007-1423.2020.10.003 LIU Yang. Inverse kinematics solution of robot manipulators based on multi-objective particle swarm optimization[J]. Modern Computer,2020(10):13-17. DOI: 10.3969/j.issn.1007-1423.2020.10.003
[5] 郑雪芳,林意. 基于改进萤火虫算法的冗余机器人轨迹规划[J]. 组合机床与自动化加工技术,2019(12):80-84. DOI: 10.13462/j.cnki.mmtamt.2019.12.020 ZHENG Xuefang,LIN Yi. Trajectory planning for redundant robot based on improved glowworm swarm optimization algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique,2019(12):80-84. DOI: 10.13462/j.cnki.mmtamt.2019.12.020
[6] 樊华羽,詹浩,程诗信,等. 基于α-stable分布的多目标粒子群算法研究及应用[J]. 西北工业大学学报,2019,37(2):232-241. DOI: 10.3969/j.issn.1000-2758.2019.02.004 FAN Huayu,ZHAN Hao,CHENG Shixin,et al. Research and application of multi-objective particle swarm optimization algorithm based on α-stable distribution[J]. Journal of NorthWestern Polytechnical University,2019,37(2):232-241. DOI: 10.3969/j.issn.1000-2758.2019.02.004
[7] 齐飞,平雪良,刘洁,等. 工业机器人误差补偿及冗余参数研究[J]. 机械设计,2017,34(2):17-22. DOI: 10.13841/j.cnki.jxsj.2017.02.004 QI Fei,PING Xueliang,LIU Jie,et al. Error compensation and parameters redundancy research of industrial robot[J]. Journal of Machine Design,2017,34(2):17-22. DOI: 10.13841/j.cnki.jxsj.2017.02.004
[8] 王宪伦,喻洋,王道全,等. 凿岩机器人的建模与运动学分析[J]. 矿山机械,2016,44(1):90-93. DOI: 10.16816/j.cnki.ksjx.2016.01.022 WANG Xianlun,YU Yang,WANG Daoquan,et al. Modeling and kinematics analysis of rock drilling robot[J]. Mining & Processing Equipment,2016,44(1):90-93. DOI: 10.16816/j.cnki.ksjx.2016.01.022
[9] 徐勤宪,郭治富. 锚杆钻车三角钻臂的运动学研究[J]. 煤矿机械,2019,40(6):25-27. DOI: 10.13436/j.mkjx.201906008 XU Qinxian,GUO Zhifu. Kinematics research of triangular drill arm of bolt drilling rig[J]. Coal Mine Machinery,2019,40(6):25-27. DOI: 10.13436/j.mkjx.201906008
[10] 武少华,高岳林. 粒子群算法的改进与比较研究[J]. 合肥工业大学学报(自然科学版),2019,42(2):184-188,194. DOI: 10.3969/j.issn.1003-5060.2019.02.008 WU Shaohua,GAO Yuelin. Improvement and comparison of particle swarm optimization[J]. Journal of Hefei University of Technology(Natural Science),2019,42(2):184-188,194. DOI: 10.3969/j.issn.1003-5060.2019.02.008
[11] 梁樱馨,田浩杉. 基于细菌觅食与粒子群的改进粒子群算法[J]. 电子科技,2017,30(4):79-82. LIANG Yingxin,TIAN Haoshan. Improved hybrid algorithm based on bacterial foraging and particle swarm optimization[J]. Electronic Science and Technology,2017,30(4):79-82.
[12] 潘勇,郭晓东. 一种基于遗传算法改进的粒子群优化算法[J]. 计算机应用与软件,2011,28(9):222-224. DOI: 10.3969/j.issn.1000-386X.2011.09.067 PAN Yong,GUO Xiaodong. An improved particle swarm optimization algorithm based on genetic algorithm[J]. Computer Applications and Software,2011,28(9):222-224. DOI: 10.3969/j.issn.1000-386X.2011.09.067
[13] 张晓莉,王秦飞,冀汶莉. 一种改进的自适应惯性权重的粒子群算法[J]. 微电子学与计算机,2019,36(3):66-70. DOI: 10.19304/j.cnki.issn1000-7180.2019.03.014 ZHANG Xiaoli,WANG Qinfei,JI Wenli. An improved particle swarm optimization algorithm for adaptive inertial weights[J]. Microelectronics & Computer,2019,36(3):66-70. DOI: 10.19304/j.cnki.issn1000-7180.2019.03.014
[14] SEKIGUCHI S, KIKUUWE, R. A stable algorithm for unsolvable inverse kinematics of a class of six-DoF manipulators[C]. IEEE/SICE International Symposium on System Integration, Honolulu, 2020: 1521-1529.
[15] 黄开启,魏文彬,陈荣华,等. 凿岩机器人钻臂定位误差补偿控制交叉精英反向粒子群优化算法[J]. 机械科学与技术,2018,37(7):1005-1012. DOI: 10.13433/j.cnki.1003-8728.2018.0702 HUANG Kaiqi,WEI Wenbin,CHEN Ronghua,et al. CEOPSO algorithm for positioning error compensation control of rock drilling robotic drilling arm[J]. Mechanical Science and Technology for Aerospace Engineering,2018,37(7):1005-1012. DOI: 10.13433/j.cnki.1003-8728.2018.0702
[16] 王涛. 非线性权重和柯西变异的蝗虫算法[J]. 微电子学与计算机,2020,37(5):82-86. DOI: 10.19304/j.cnki.issn1000-7180.2020.05.016 WANG Tao. Grasshopper optimization algorithm with nonlinear weight and cauchy mutation[J]. Microelectronics & Computer,2020,37(5):82-86. DOI: 10.19304/j.cnki.issn1000-7180.2020.05.016
[17] 康岚兰,董文永,田降森. 一种自适应柯西变异的反向学习粒子群优化算法[J]. 计算机科学,2015,42(10):226-231. KANG Lanlan,DONG Wenyong,TIAN Jiangsen. Opposition-based particle swarm optimization with adaptive Cauchy mutation[J]. Computer Science,2015,42(10):226-231.
[18] 于建芳,刘升,韩斐斐,等. 基于柯西变异的蚁狮优化算法[J]. 微电子学与计算机,2019,36(6):45-49,54. DOI: 10.19304/j.cnki.issn1000-7180.2019.06.010 YU Jianfang,LIU Sheng,HAN Feifei,et al. Ant lion optimization algorithm based on Cauchy variation[J]. Microelectronics & Computer,2019,36(6):45-49,54. DOI: 10.19304/j.cnki.issn1000-7180.2019.06.010
[19] 徐浩天,季伟东,孙小晴,等. 基于正态分布衰减惯性权重的粒子群优化算法[J]. 深圳大学学报(理工版),2020,37(2):208-213. DOI: 10.3724/SP.J.1249.2020.02208 XU Haotian,JI Weidong,SUN Xiaoqing,et al. A PSO algorithm with inertia weight decay by normal distribution[J]. Journal of Shenzhen University(Science and Engineering),2020,37(2):208-213. DOI: 10.3724/SP.J.1249.2020.02208
[20] 李俊,汪冲,李波,等. 基于多策略协同作用的粒子群优化算法[J]. 计算机应用,2016,36(3):681-686. DOI: 10.11772/j.issn.1001-9081.2016.03.681 LI Jun,WANG Chong,LI Bo,et al. Particle swarm optimization algorithm based on multi-strategy synergy[J]. Journal of Computer Applications,2016,36(3):681-686. DOI: 10.11772/j.issn.1001-9081.2016.03.681
[21] 韩玉辉. 液压凿岩台车自动定位钻孔关键技术研究[D]. 徐州: 中国矿业大学, 2019. HAN Yuhui. Research on key technologies of automatic location drilling for rock drilling jumbo[D]. Xuzhou: China University of Mining and Technology, 2019.
[22] 冯帆. 红外视觉定位的机械臂控制算法研究与实现[D]. 西安: 西安工业大学, 2019. FENG Fan. Research and implementation of manipulator control algorithm for infrared vision positioning[D]. Xi'an: Xi'an Technological University, 2019.
-
期刊类型引用(2)
1. 陈伟，陈志良，侯强. 煤矿井下液压锚杆钻机钻臂定位控制方法. 自动化与仪表. 2024(08): 29-33+39 . 
百度学术
2. 李富强. 锚杆钻车施工影响因素分析. 中国机械. 2023(33): 90-93 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 192
- HTML全文浏览量: 57
- PDF下载量: 18
- 被引次数: 4
