Bearing intelligent fault diagnosis
-
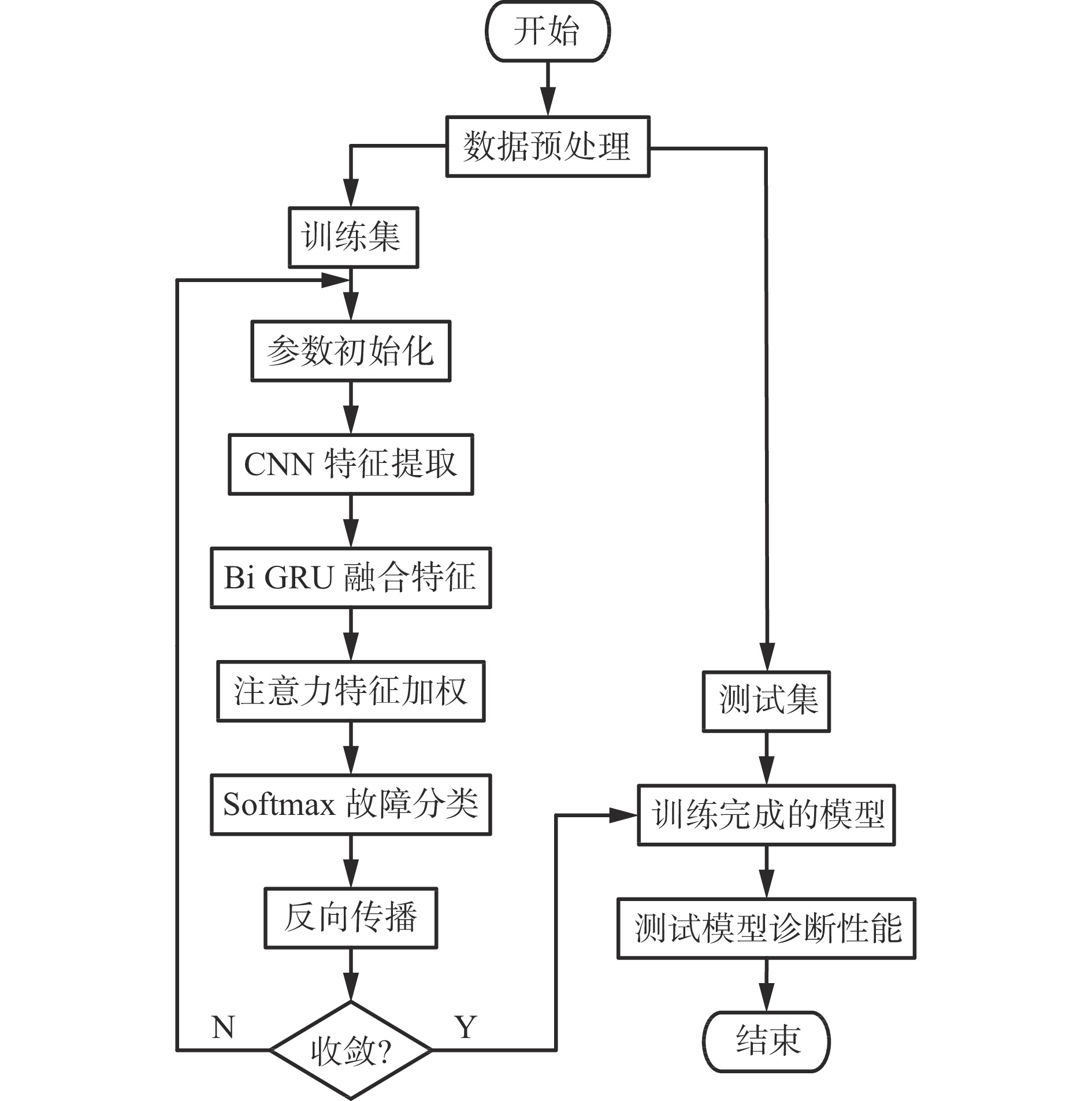
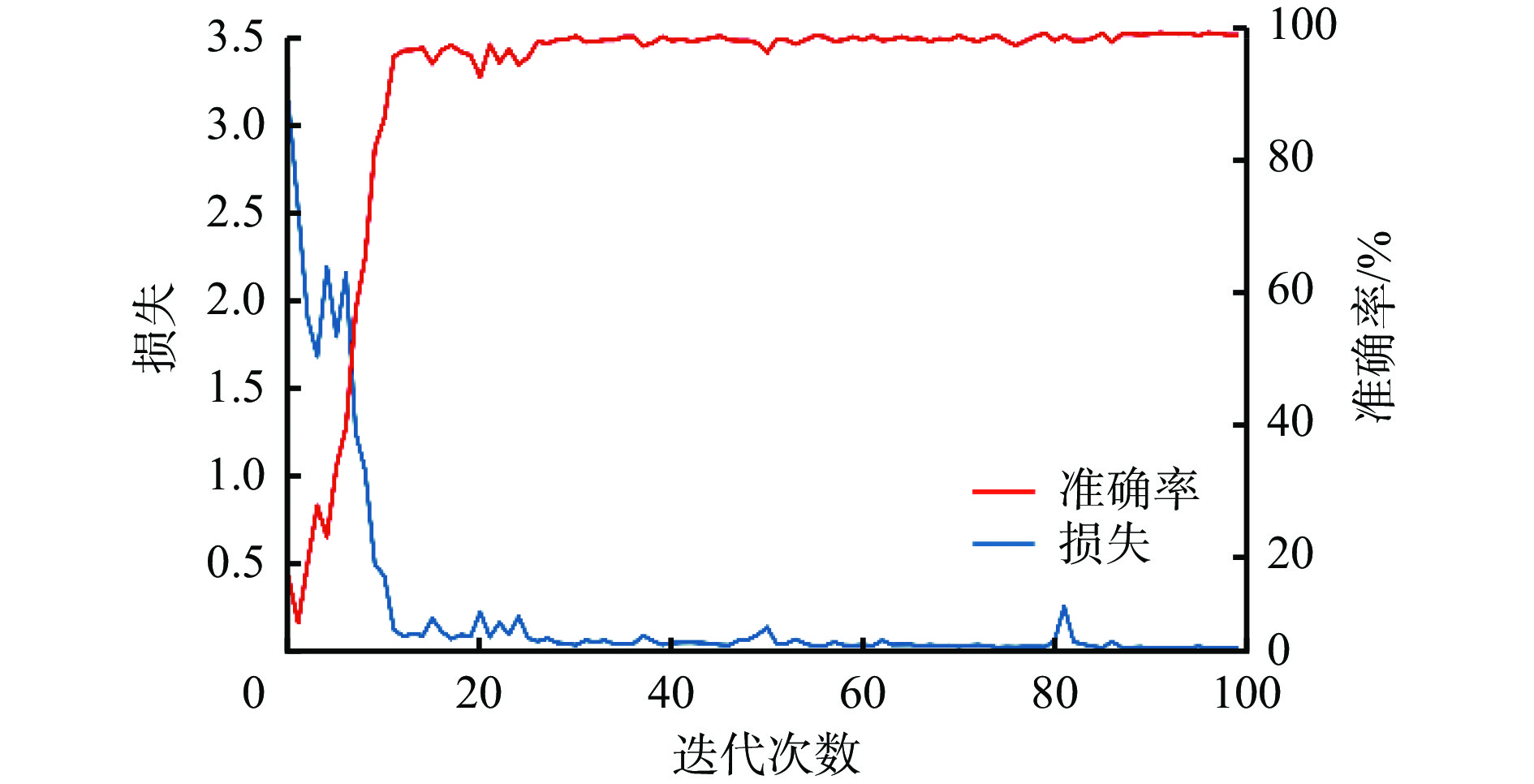
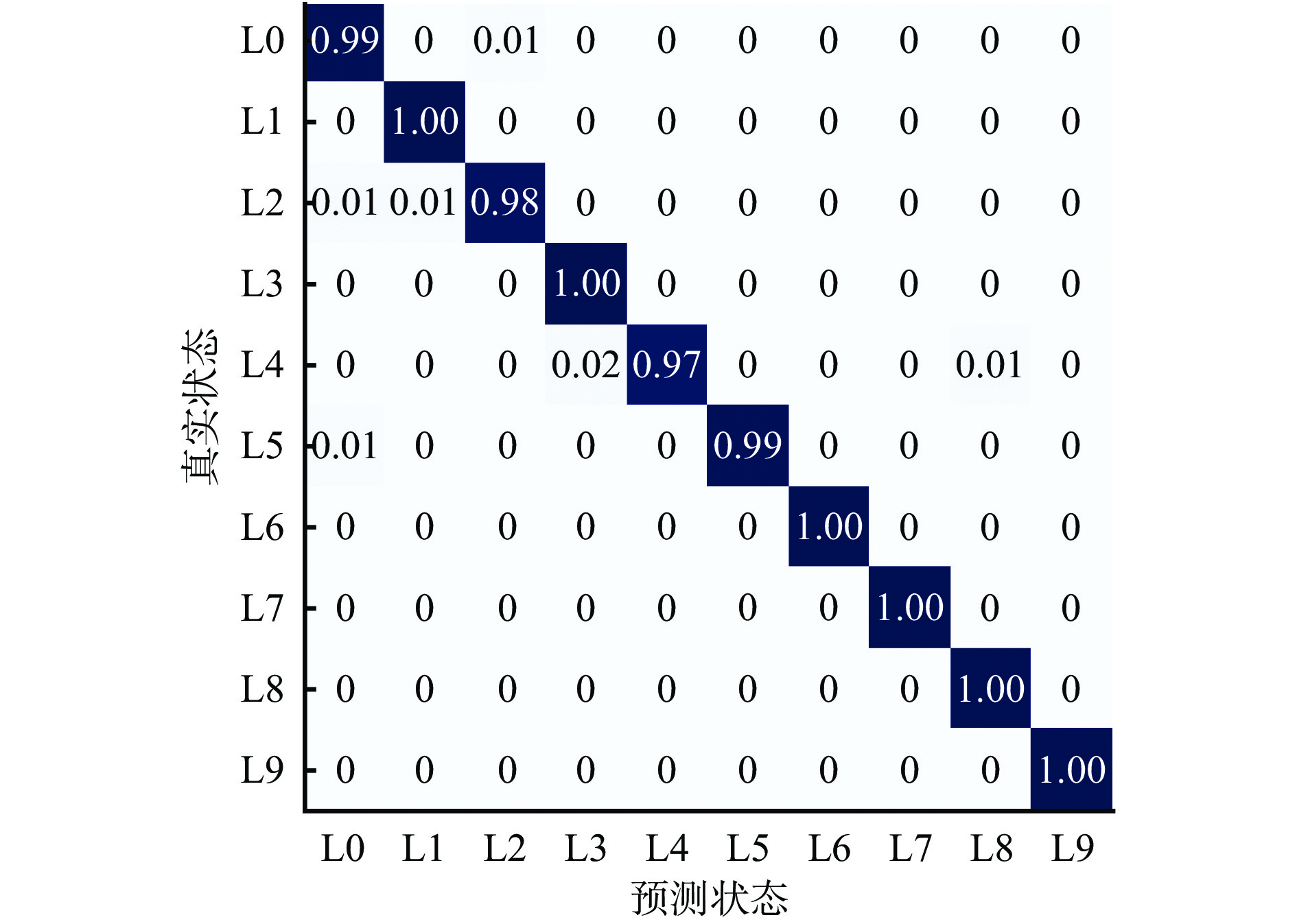
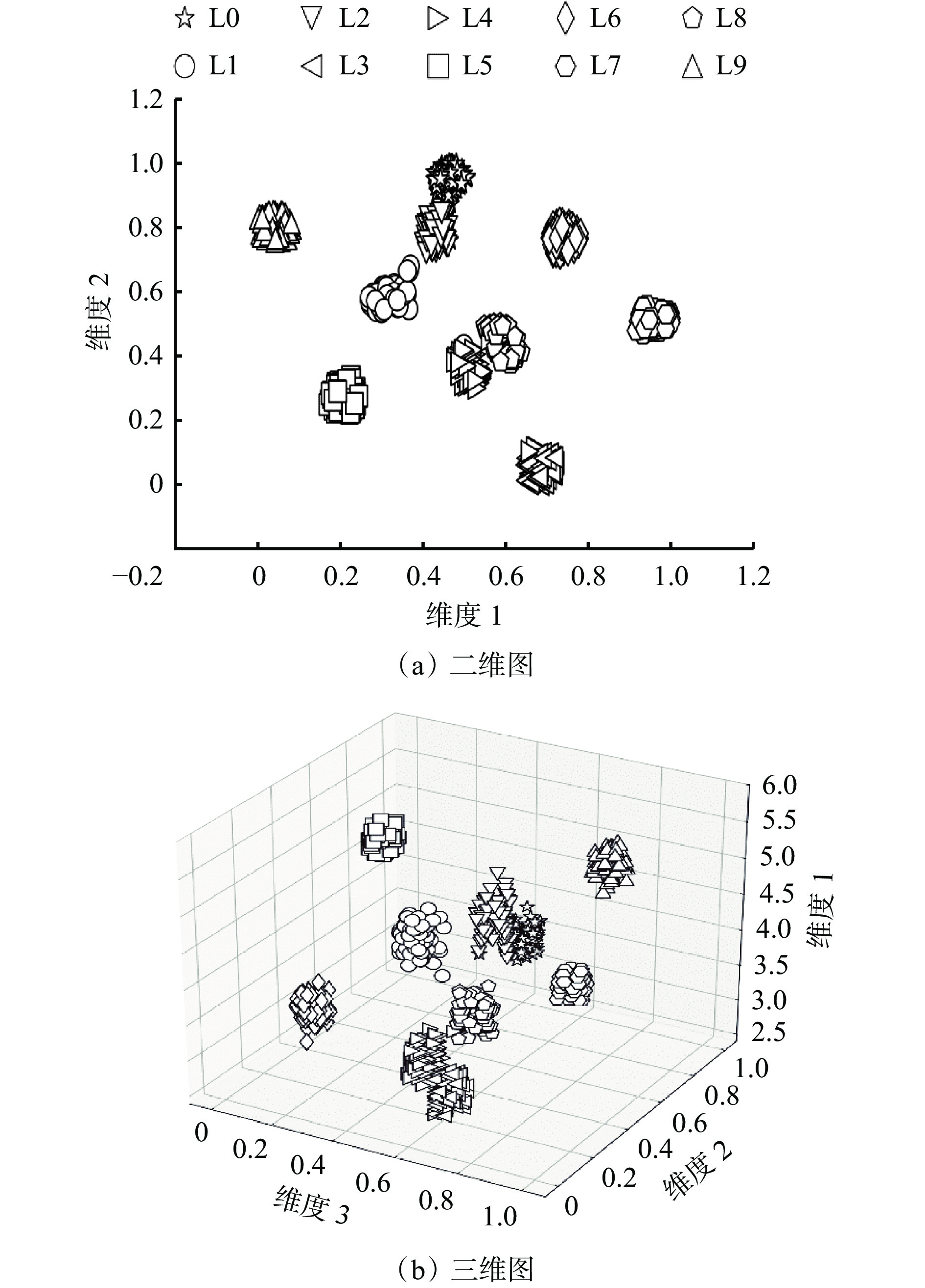
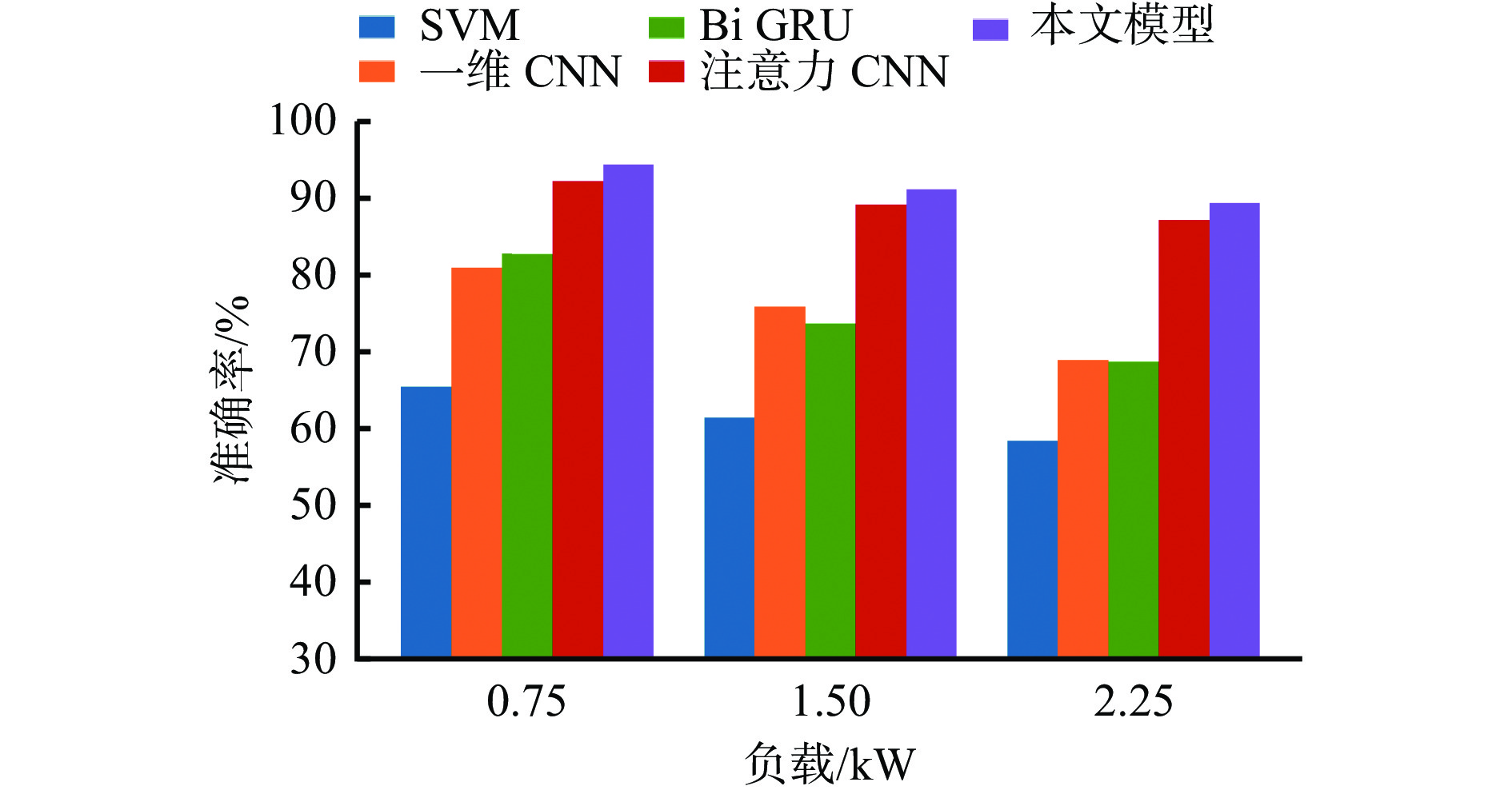
摘要: 轴承振动信号作为一种时间序列数据，其时间维度特征在分类中起着关键作用，单独使用卷积神经网络（CNN）进行轴承故障诊断会造成时间维度信息的丢失，导致诊断精度下降。针对上述问题，提出了一种结合一维CNN、双向门控循环单元(Bi GRU)和注意力机制的轴承故障诊断模型。首先利用CNN自适应提取一维振动信号局部空间特征；然后将该特征信息作为Bi GRU的输入，利用Bi GRU将提取的特征信息进行时间维度的融合，并引入注意力机制对多个时刻的特征信息进行加权，提取出更关键的故障特征；最后将故障特征输入全连接层得到分类结果，实现轴承智能故障诊断。实验结果表明：① 在测试集混淆矩阵上，轴承运行状态基本分类正确，只有部分标记类型没有被完全分类正确，但是召回率达到了95%以上，总的故障识别准确率为99.3%。② 利用t−SNE技术对降维处理后的数据进行可视化，轴承各运行状态的数据很好地聚集在各自的空间内，只有少量数据被混杂到其他区域，说明该模型具有较强的特征提取能力。③ 在恒定负载情况下，该模型故障诊断准确率较一维CNN、Bi GRU和注意力CNN等模型的平均准确率分别提高了0.8%、0.6%和0.3%。④ 在变负载情况下，与SVM(支持向量机)、一维CNN、Bi GRU和注意力CNN等模型相比，该模型具有更好的稳定性，当负载为2.25 kW时，准确率达85%以上。该模型既具有一维CNN局部特征提取能力，又具有Bi GRU时间依赖信息的建模能力，能够在获取轴承信号局部复杂特征后进一步融入特征之间的时间维度信息，同时注意力机制能进一步关注与故障更相关特征，因此具有较好的精度。Abstract: Bearing vibration signal is a kind of time series data, and its time dimension characteristic plays a key role in classification. Using convolutional neural network (CNN) alone to diagnose bearing fault will cause the loss of time dimension information. This results in the decline of diagnosis accuracy. To solve the above problems, a bearing fault diagnosis model combining one-dimensional CNN, bidirectional gated recurrent unit (Bi GRU) and attention mechanism is proposed. Firstly, CNN is used to adaptively extract the local space characteristic of one-dimensional vibration signals. Secondly, the characteristic information is taken as the input of the Bi GRU. Bi GRU is used to perform time dimension fusion on the extracted characteristic information. The attention mechanism is introduced to weigh the characteristic information of a plurality of moments so as to extract a more critical fault characteristic. Finally, the fault characteristic is input into a full connection layer to obtain a classification result, so as to realize intelligent fault diagnosis of the bearing. The experimental result shows the following points. ① On the confusion matrix of the test set, the classification of the bear running state is basically correct. Only some mark types are not completely classified correctly. But the recall rate is more than 95%, and the total fault recognition accuracy rate is 99.3%. ② The t-SNE technology is used to visualize the data after dimensionality reduction processing. The data of each running state of the bearing are well gathered in their own space. Only a small amount of data are mixed into other areas, which shows that the model has strong characteristic extraction capability. ③ Under the condition of constant load, the average accuracy of fault diagnosis of this model is 0.8%, 0.6% and 0.3% higher than that of one-dimensional CNN, Bi GRU and attention CNN models respectively. ④ Under the condition of variable load, this model has better stability than SVM, one-dimensional CNN, Bi GRU, attention CNN and other models. When the load is 2.25 kW, the accuracy rate is more than 85%. The model has the capability to extract one-dimensional CNN local characteristics and the capability to model Bi GRU time-dependent information. The model can further fuse time dimension information among the characteristics after acquiring the bear signal local complex characteristics. And the attention mechanism can further pay attention to the characteristics more relevant to faults. Therefore, the model has better precision.
-
0. 引言
煤矿井下环境的复杂扰动和回采过程中煤层顶板、底板的不规则变化，造成液压支架支护位姿发生变化，可能造成支护失效，导致安全事故发生[1-3]。迅速且精确地获取液压支架支护位姿信息是当前综采工作面智能化进程中亟待攻克的关键技术挑战之一[4-5]。
在液压支架姿态感知研究方面，郭周斌[6]采用压力传感器、行程传感器和倾角传感器对液压支架位姿进行感知，但未考虑到井下恶劣环境导致传感器产生误差，未采取有效的滤波手段，缺乏多传感器间的数据融合。谢明明[7]采用双轴倾角传感器对液压支架构件的倾角数据进行采集，实现了对液压支架关键构件姿态角度的计算。王忠乐[8]利用测高传感器配合倾角传感器对液压支架高度、倾角变化情况进行分析，实现了支架姿态实时监测，但仅在底座上安装1个倾角传感器，可能导致测得的姿态与真实姿态存在较大误差。谢嘉成[9]将双轴倾角传感器布置在液压支架关键构件处，实现了对液压支架的位姿监测，但在复杂工况下监测误差可能较大。张坤等[10]利用超声波传感器与九轴姿态传感器实现了对超前液压支架姿态的感知，但仅采用卡尔曼滤波算法易陷入局部极小值点，寻优结果存在误差。崔宽宽[11]将倾角传感器部署于液压支架顶梁、底座与后连杆中，通过卡尔曼滤波算法提升位姿监测的准确性，但卡尔曼滤波算法常用于求解线性问题，而液压支架位姿感知属于非线性系统状态估计问题，可能导致估计误差偏大。Chen Ningning等[12]将研制的光纤光栅倾角传感器和光纤光栅压力传感器安装于液压支架上，实现了对液压支架位姿数据和压力数据的实时监测，虽然光纤光栅传感器具有高精度和抗电磁干扰的优点，但传感器受到噪声、振动等因素的干扰，未采用滤波算法进一步提升精度。Chen Hongyue等[13]采用广角超声波传感器与倾角传感器协同监测，通过融合算法对传感器数据进行融合，实现恶劣井下环境下液压支架的姿态感知，但仅能感知得到偏航角与横滚角数据，未涉及俯仰角数据。Gao Kuidong等[14]将拉线位移传感器、视觉传感器、惯性测量单元应用于液压支架位姿感知，并引入粒子群优化算法，但视觉传感器在井下恶劣环境中易受煤炭粉尘、外界振动等因素的影响，导致位姿感知精度不高，同时所需成本较高。
为了精确感知扰动环境下液压支架位姿，本文提出一种基于多传感器融合的液压支架位姿精确感知方法。在液压支架顶梁、掩护梁、后连杆和底座4个构件上部署九轴姿态传感器采集数据，并解算出其所在构件的横滚角、俯仰角和偏航角等位姿数据；通过无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法和改进梯度下降（Improved Gradient Descent，IGD）算法对位姿数据进行滤波处理；采用自适应加权融合算法对滤波处理后的液压支架顶梁和底座的偏航角和横滚角数据进行融合处理，实现液压支架位姿精确感知。
1. 液压支架支护位姿精确感知流程
液压支架支护位姿精确感知流程如图1所示。通过在液压支架各关键构件中部署九轴姿态传感器，解算出其所在构件的横滚角、俯仰角和偏航角等位姿数据，并通过IGD−UKF算法进行滤波处理；为消除外界振动、噪声等因素引起的液压支架顶梁和底座传感器数据误差，利用自适应加权融合算法对滤波处理后的液压支架顶梁与底座横滚角和偏航角位姿数据进行融合，输出精确的液压支架位姿数据。
![]()
图 1 液压支架支护位姿精确感知流程Figure 1. Precise perception process for position and posture of hydraulic supports2. 液压支架关键构件位姿数据解算
建立地理惯性坐标系[15]，定义正东方向为xn轴正方向，正北方向为yn轴正方向，根据右手正交坐标系定则，定义垂直于大地内部指向天空为zn轴正方向；建立液压支架顶梁坐标系，定义xb轴正方向为液压支架随采煤机推移方向，zb轴正方向垂直于液压支架顶梁向上，yb轴正方向指向液压支架一侧且与xb轴、zb轴组成右手正交坐标系。将九轴姿态传感器分别布置于液压支架顶梁、掩护梁、后连杆和底座4个构件上，如图2所示。九轴姿态传感器由三轴陀螺仪、三轴加速度计、三轴磁力计组成，分别采集所安装构件的相关数据，经解算得到所安装构件的俯仰角、横滚角和偏航角等位姿数据[16-18]，并用四元数法[19]表示。
3. 基于IGD−UKF的液压支架关键构件位姿数据滤波
在液压支架支护过程中，由于液压支架工作循环中各构件间相互运动，受摩擦、振动、噪声等扰动因素影响，若仅依靠在液压支架关键构件上九轴姿态传感器的输出数据来判断液压支架位姿，会出现较大的计算误差。因此采用IGD−UKF滤波算法[20]对液压支架关键构件的位姿数据进行滤波处理。IGD−UKF算法流程如图3所示，通过状态预测和观测预测得到变量和误差协方差矩阵，并计算增益矩阵，在目标函数的迭代过程中添加扰动因子，在状态更新中利用IGD优化UKF算法的噪声协方差，输出最优后验估计，提高复杂环境下状态估计的精度。
4. 基于自适应加权融合算法的液压支架横滚角和偏航角数据融合
液压支架随采煤机向前推进过程中，因截割量存在差别会导致底板出现凹凸不平。为使液压支架保持有效支护，即液压支架顶梁与顶板贴合、底座与底板贴合，在这种情况下可能会导致液压支架顶梁与底座发生不同角度的俯仰；但对于横滚角和偏航角来说，液压支架在支护中由于自身无法发生扭转，理论上液压支架顶梁和底座的横滚角和偏航角是相同的；但在实际工作过程中，因为振动、噪声等其他外界因素的影响，液压支架顶梁和底座的横滚角和偏航角也会出现偏差。为消除偏差，采用自适应加权融合算法对权重进行自适应分配，将多个传感器数据进行融合[21]。
自适应加权融合算法通过数学优化方法在约束条件下求解最优权重，确保融合结果满足总方差最小原则。自适应加权融合算法流程如图4所示。对经IGD−UKF滤波算法处理的液压支架顶梁和底座的横滚角和偏航角数据点进行方差求解，判断是否满足总方差最小原则，若满足则根据数据点方差大小对数据点权重进行自适应分配，以保证输出最终位姿融合结果具有较高的准确性。
最终获得的融合数据可表示为
$$ x' = \sum\limits_{i = 1}^j {{\omega _i}\bar{{x_i}} \left( k \right)} $$ (1) 式中：$ \bar{{x_i}} \left( k \right) $为传感器i采集k组数据得到的均值；$ {\omega _i} $为传感器i测得数据的权值；j为传感器个数。
融合数据的方差为
$$ {\bar \sigma ^2} = \frac{1}{j}\sum\limits_{i = 1}^j {{\omega _i}\mu _i^2} $$ (2) 式中$ \mu _i^{} $为传感器i的测量值与真实值间误差。
随着权重分配的动态调整，方差趋于减小，从而提高数据精度。
5. 液压支架支护位姿精确感知实验
搭建液压支架位姿感知实验平台，如图5所示。通过顶板控制油缸带动顶板运动，以模拟顶板对液压支架顶梁施加的压力，同时顶板和底板均可前后左右倾斜，以模拟开采中顶板和底板的变化；将HWT905−CAN九轴姿态传感器分别安装在液压支架顶梁、掩护梁、后连杆和底座上，并通过RS485−USB模块建立九轴姿态传感器与数据采集平台之间的通信；通过实验控制台控制液压支架与顶板运动，液压泵站为各液压部件的伸缩提供动力；九轴姿态传感器采集液压支架在顶梁低头和抬头、底座低头和抬头、液压支架左倾和右倾、液压支架左偏和右偏等情况下的位姿数据，采集频率为10 Hz。采集数据时对液压支架顶梁进行手动敲击，以模拟振动干扰。
![]()
图 5 液压支架位姿感知实验平台Figure 5. Experimental platform for position and posture perception of hydraulic supports5.1 IGD−UKF算法滤波效果
选取九轴姿态传感器采集并解算出的底座和顶梁各600组包含俯仰角、横滚角、偏航角的数据导入Matlab软件中，分别利用UKF算法和IGD−UKF算法进行滤波处理，效果如图6所示。可看出相对于UKF算法，IGD−UKF算法处理后的数据曲线波动趋于平缓，在抑制振荡、减小振幅上的效果明显。
![]()
图 6 UKF与IGD−UKF滤波效果对比Figure 6. Comparison of filtering effects between UKF and IGD-UKF5.2 自适应加权融合算法的融合效果
将经过IGD−UKF算法处理后的液压支架顶梁与底座的横滚角、偏航角数据导入自适应加权融合算法模型中，得到的融合结果与仅经过IGD−UKF算法处理后的液压支架顶梁与底座的横滚角、偏航角进行对比，如图7所示，可看出自适应加权融合算法抑制了顶梁与底座横滚角、俯仰角数据波动。利用Matlab软件标记出图7的最小误差与最大误差，通过提取各样本点数据的绝对误差并求解平均值，得到平均绝对误差，结果见表1，可看出自适应加权融合算法提升了液压支架位姿的感知精度。
![]()
图 7 液压支架顶梁与底座姿态角融合前后效果对比Figure 7. Comparison of effects before and after fusion of attitude angles of top beam and base of hydraulic supports表 1 自适应加权融合算法融合位姿数据误差结果Table 1. Error results of position and posture data fused by adaptive weighted fusion algorithm（°） 液压支架姿态角 最小误差 最大误差 平均绝对误差 偏航角 0.001 8 0.025 1 0.004 8 横滚角 0.001 4 0.028 1 0.004 7 6. 结论
1） 将九轴姿态传感器安装于液压支架顶梁、掩护梁、后连杆和底座进行数据采集并解算出所在构件的位姿数据，利用IGD−UKF算法对位姿数据进行滤波处理，抑制了数据振荡。通过自适应加权融合算法对滤波处理后不同构件的相同位姿数据进行融合，以减小振动等对液压支架位姿感知精度的干扰。
2） 搭建了液压支架位姿感知实验平台，开展了IGD−UKF算法滤波实验和自适应加权融合算法融合实验，得出液压支架偏航角误差为0.001 8～0.025 1°，平均绝对误差为0.004 8°，横滚角误差为0.001 4～0.028 1°，平均绝对误差为0.004 7°，实现了液压支架位姿的精确感知。
-
表 1 故障诊断模型结构参数
Table 1 Parameters of the fault diagnosis model structure
层数 结构参数 输出特征 M0 输入层 2048 M1 卷积层 (64×1/16/16) 128×16 M2 池化层 (2×1/2) 64×16 M3 卷积层(5×1/1/32) 64×32 M4 池化层(2×1/2) 32×32 M5 Bi GRU层（32） 32×64 M6 注意力模块 64 M7 全连接层 10 M8 Softmax层 10 
下载: 导出CSV
表 2 实验样本划分
Table 2 Experimental sample division
训练样本数 测试
样本数故障
种类故障
直径/mm类型
标记400 100 滚动体 0.177 8 L0 400 100 滚动体 0.355 6 L1 400 100 滚动体 0.533 4 L2 400 100 内圈 0.177 8 L3 400 100 内圈 0.355 6 L4 400 100 内圈 0.533 4 L5 400 100 外圈 0.177 8 L6 400 100 外圈 0.355 6 L7 400 100 外圈 0.533 4 L8 400 100 正常 0 L9
下载: 导出CSV
表 3 5种故障诊断模型的准确率对比
Table 3 Accuracy comparison of five kinds of fault diagnosis models
模型 平均准确率/% SVM 90.3 一维CNN 98.5 Bi GRU 98.7 注意力CNN 99.0 本文模型 99.3
下载: 导出CSV
-
[1] 宫涛,杨建华,单振,等. 强噪声背景与变转速工况条件下滚动轴承故障诊断研究[J]. 工矿自动化,2021,47(7):63-71. GONG Tao,YANG Jianhua,SHAN Zhen,et al. Research on rolling bearing fault diagnosis under strong noise background and variable speed working condition[J]. Industry and Mine Automation,2021,47(7):63-71.
[2] 黄重谦. 基于多隐层小波卷积极限学习神经网络的滚动轴承故障识别[J]. 工矿自动化,2021,47(7):63-71. HUANG Zhongqian. Fault identification of rolling bearing based on multi hidden layers wavelet convolution extreme learning neural network[J]. Industry and Mine Automation,2021,47(7):63-71.
[3] 吴静然,丁恩杰,崔冉,等. 采用多尺度注意力机制的旋转机械故障诊断方法[J]. 西安交通大学学报,2020,54(2):51-58. WU Jingran,DING Enjie,CUI Ran,et al. A diagnostic approach for rotating machinery using multi-scale feature attention mechanism[J]. Journal of Xi'an Jiaotong University,2020,54(2):51-58.
[4] HE Miao,HE D. Deep learning based approach for bearing fault diagnosis[J]. IEEE Transactions on Industry Applications,2017,53(3):3057-3065. DOI: 10.1109/TIA.2017.2661250
[5] LI Xiangong,ZHANG Yuzhi,WANG Fuqi,et al. A fault diagnosis method of rolling bearing based on wavelet packet analysis and deep forest[J]. Symmetry,2022,14(2):267. DOI: 10.3390/sym14020267
[6] 汪峰,周凤星,严保康. 基于特征量融合和支持向量机的滚动轴承故障诊断[J]. 科学技术与工程,2022,22(6):2351-2356. DOI: 10.3969/j.issn.1671-1815.2022.06.026 WANG Feng,ZHOU Fengxing,YAN Baokang. Rolling bearing fault diagnosis based on feature fusion and support vector machine[J]. Science Technology and Engineering,2022,22(6):2351-2356. DOI: 10.3969/j.issn.1671-1815.2022.06.026
[7] 雷亚国,贾峰,周昕,等. 基于深度学习理论的机械装备大数据健康监测方法[J]. 机械工程学报,2015,51(21):49-56. DOI: 10.3901/JME.2015.21.049 LEI Yaguo,JIA Feng,ZHOU Xi,et al. A deep learning based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering,2015,51(21):49-56. DOI: 10.3901/JME.2015.21.049
[8] WANG Lihua,ZHAO Xiaoping,WU Jiaxin,et al. Motor fault diagnosis based on short-time fourier transform and convolutional neural network[J]. Chinese Journal of Mechanical Engineering,2017,30(6):1357-1368. DOI: 10.1007/s10033-017-0190-5
[9] LEVENT E,TURKER I,SERKAN K. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier[J]. Journal of Signal Processing Systems for Signal,Image,and Videl Technology,2019,91(2):179-189. DOI: 10.1007/s11265-018-1378-3
[10] 李长文,程泽银,张小刚,等. 基于深度残差网络的采煤机摇臂齿轮故障诊断[J]. 工矿自动化,2021,47(3):71-78. LI Changwen,CHENG Zeyin,ZHANG Xiaogang,et al. Fault diagnosis of shearer rocker gear based on deep residual network[J]. Industry and Mine Automation,2021,47(3):71-78.
[11] 姜家国,郭曼利,杨思国. 基于GAF和DenseNet的滚动轴承故障诊断方法[J]. 工矿自动化,2021,47(8):84-89. JIANG Jiaguo,GUO Manli,YANG Siguo. Fault diagnosis of rolling barings based on GAF and DenseNet[J]. Industry and Mine Automation,2021,47(8):84-89.
[12] LEI Jinhao,LIU Chao,JIANG Dongxiang. Fault diagnosis of wind turbine based on long short-term memory networks[J]. Renewable Energy,2019,133:422-432. DOI: 10.1016/j.renene.2018.10.031
[13] 樊家伟,郭瑜,伍星,等. 基于LSTM神经网络和故障特征增强的行星齿轮箱故障诊断[J]. 振动与冲击,2021,40(20):271-277. DOI: 10.13465/j.cnki.jvs.2021.20.034 FAN Jiawei,GUO Yu,WU Xing,et al. Fault diagnosis of planetary gearboxes based on LSTM neural network and fault feature enhancement[J]. Journal of Vibration and Shock,2021,40(20):271-277. DOI: 10.13465/j.cnki.jvs.2021.20.034
[14] 张立鹏,毕凤荣,程建刚,等. 基于注意力Bi GRU的机械故障诊断方法研究[J]. 振动与冲击,2021,40(5):113-118. ZHANG Lipeng,BI Fengrong,CHENG Jiangang,et al. Mechanical fault diagnosis method based on attention Bi GRU[J]. Journal of Vibration and Shock,2021,40(5):113-118.
[15] 吉兴全,曾若海,张玉敏,等. 基于注意力机制的CNN-LSTM短期电价预测[J]. 电力系统保护玉控制,2022,50(17):125-132. JI Xingquan,ZENG Ruohai,ZHANG Yumin,et al. CNN-LSTM short-term electricity prediction based on an attention mechanism[J]. Power System Protection and Control,2022,50(17):125-132.
[16] 毛煜,尚海昆,于卓琦. 基于长短期记忆网络的电网同调机群快速辨识[J]. 电气工程学报,2022,17(2):201-207. MAO Yu,SHANG Haikun,YU Zhuoqi. A fast prediction method of coherernt generators based on long short-term memory network[J]. Journal of Electrical Engineering,2022,17(2):201-207.
[17] MAATEN L V,HINTON G. Visualizing data using t-SNE[J]. Journal of Machine Learning Research,2008,9(11):2579-2605.
计量
- 文章访问数: 381
- HTML全文浏览量: 113
- PDF下载量: 57
