Bearing fault diagnosis based on harmonic matching compensation and keyless phase order tracking
-
摘要: 煤矿机械设备轴承在强冲击、大载荷工况下产生的振动信号表现出强烈的瞬态非平稳与局部非线性特性。经典的时域统计分析方法和全局域变换方法难以识别故障特征；传统阶次跟踪方法存在设备安装不便、难以获取瞬时频率的问题；传统的无键相阶次跟踪方法在转速波动剧烈的条件下估计出的瞬时频率精度低，导致故障识别效果差。针对上述问题，提出了一种基于谐波匹配补偿和无键相阶次跟踪的轴承故障诊断方法。首先，利用基于谐波匹配补偿的时频分析方法对轴承振动信号进行处理，准确估计瞬时频率；其次，通过Vold-Kalman滤波方法自适应提取谐波分量信号；再次，采用Hilbert变换计算谐波的瞬时相位，进而获得时间域与角度域的映射关系，完成原始时间域信号在角度域的重采样；最后，对重采样的信号进行快速傅里叶变换，通过分析包络阶次谱，实现轴承故障特征识别。仿真和试验结果表明，该方法估计的瞬时频率与实际值之间的最大相对误差不超过1%，表征轴承故障特征阶次准确且明显，可有效诊断轴承故障。Abstract: The vibration signals of the bearings of coal mine machanical equipment under the working conditions of strong impact and heavy load show strong transient non-stationary and local nonlinear features. It is difficult to identify the fault features by the classical time-domain statistical analysis method and the global domain transformation method. The traditional order tracking method has the problems of inconvenient equipment installation and difficulty in obtaining instantaneous frequency. The traditional keyless phase order tracking method estimates the instantaneous frequency with low precision under the condition of severe speed fluctuation. This leads to poor fault identification effect. To solve these problems, a new method of bearing fault diagnosis based on harmonic matching compensation and keyless phase order tracking is proposed. Firstly, the time-frequency analysis method based on harmonic matching compensation is used to process the bearing vibration signal and estimate the instantaneous frequency accurately. Secondly, the Vold-Kalman filtering method is used to adaptively extract the harmonic component signal. Thirdly, the Hilbert transform is used to calculate the instantaneous phase of the harmonic. The mapping relationship between the time domain and angle domain is obtained, so as to complete the resampling of the original time domain signal in the angle domain. Finally, the resampled signals are processed by fast Fourier transform (FFT). The fault features of the bearing are identified by analyzing the envelope order spectrum. The simulation and experimental results show that the maximum relative error between the estimated instantaneous frequency and the actual value is less than 1%. The feature order of bearing fault is accurate and obvious, which can effectively diagnose the bearing fault.
-
0. 引言
轴承作为煤矿机械设备关键运动部件，直接影响设备的健康状态[1-2]。因此，对煤矿机械设备轴承进行故障诊断具有重要意义。传统的轴承故障诊断方法主要分为经典的时域统计分析方法和以傅里叶理论为核心的全局域变换方法。由于煤矿机械设备运行过程中振动大、冲击强，轴承振动信号呈现出瞬态非平稳的特性[3-4]，传统的轴承故障诊断方法难以识别故障特征。
传统阶次跟踪方法是通过有键相硬件设备获取非平稳信号的瞬时频率，再计算出瞬时相位[5-7]，进一步通过重采样获取角度域的循环平稳信号，从而实现非平稳信号到循环平稳信号的转变。但煤矿机械设备工作环境恶劣，不利于有键相硬件设备的安装，导致瞬时频率获取困难，阶次跟踪难以进行，严重影响了对轴承的故障诊断。无键相阶次跟踪方法可通过振动信号直接获得瞬时频率 [8-11]，克服了对有键相硬件设备的依赖，能够很好地实现对轴承故障特征的提取。但该方法运用的前提是通过振动信号获取准确的瞬时频率，进而计算出瞬时相位。然而，煤矿机械设备振动剧烈，转速呈现出强烈的非线性特性，传统的基于短时傅里叶变换（Short Time Fourier Transform，STFT）的时频分析方法在估计该工况下的瞬时频率时鲁棒性较差。为解决该问题，文献[12]提出了一种基于Chirplet变换的瞬时频率估计方法，该方法利用Chirplet变换来逼近信号，从而实现对瞬时频率的细化，在一定程度上提高了瞬时频率的估计精度，但由于振动信号的非线性调制，在速度波动剧烈的情况下，时频分辨率较低，导致计算的瞬时相位精度不高[13-14]。文献[15]针对剧烈的非线性调制，提出了瞬时故障特征频率的概念，从轴承包络信号的时频谱中提取出瞬时频率，但在转速急剧变化的情况下，包络信号的转频由于能量较弱，无法准确估计。
本文提出了一种基于谐波匹配补偿（Harmonic Matching Compensation，HMC）的时频分析方法，可实现对轴承剧烈非平稳运行工况下瞬时频率的准确估计；进一步采用无键相阶次跟踪方法，实现对轴承故障的准确识别。
1. 基于HMC和无键相阶次跟踪的轴承故障诊断原理
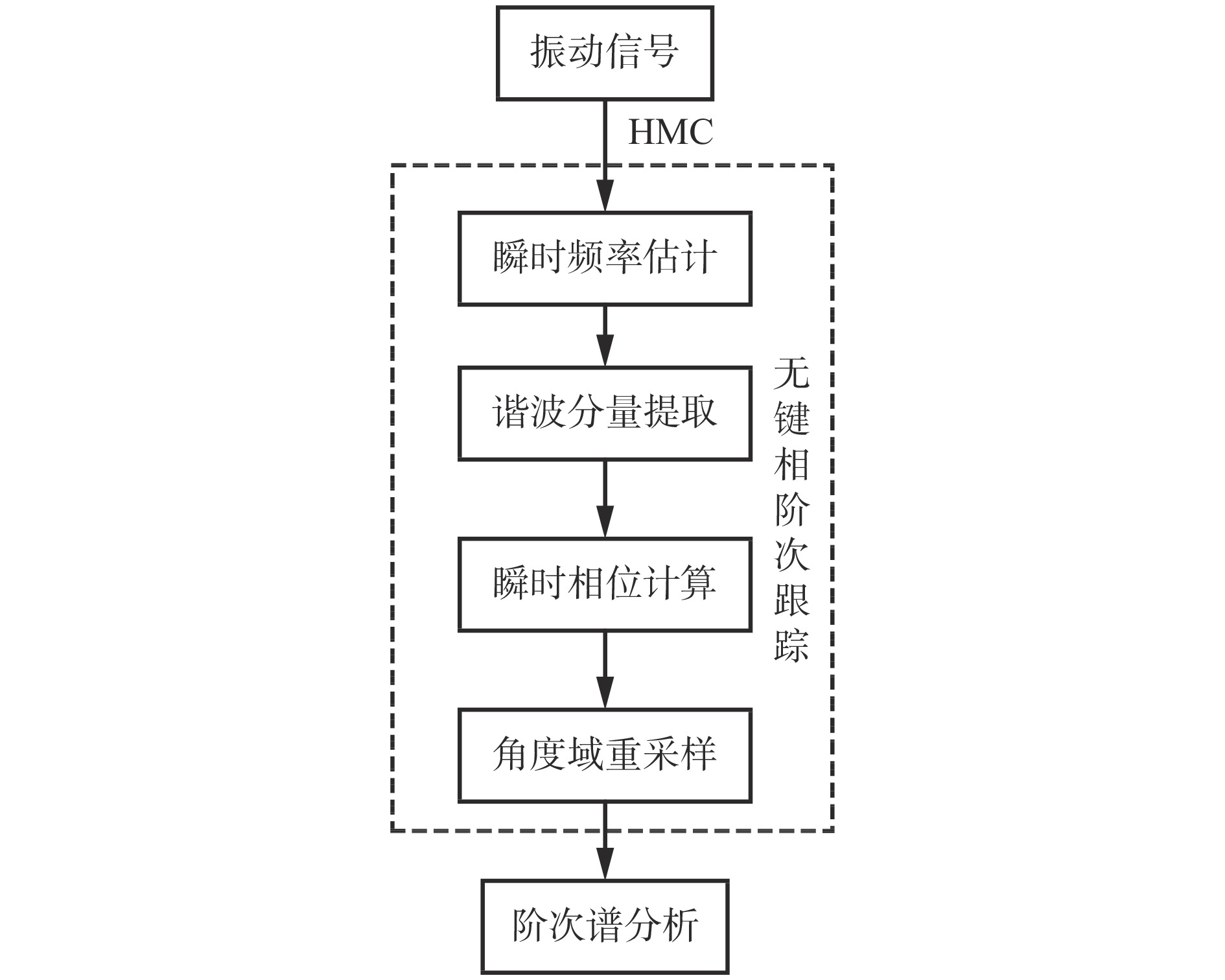
基于HMC和无键相阶次跟踪的轴承故障诊断流程如图1所示。首先，采用基于HMC的时频分析方法对振动信号进行处理，准确估计出瞬时频率。其次，由于在瞬态非平稳工况下，信号中混叠的各阶谐波分量随转速一起波动，通过Vold-Kalman滤波方法提取谐波分量信号。再次，计算出瞬时相位，进而实现信号的角度域重采样。最后，对重采样的信号进行快速傅里叶变换，从而进行阶次谱分析，识别出轴承故障特征。
![]()
图 1 基于HMC和无键相阶次跟踪的轴承故障诊断流程Figure 1. Bearing fault diagnosis process based on harmonic matching compensation and keyless phase order tracking1.1 基于HMC的瞬时频率估计
在瞬态非平稳工况下，对于一个有限的能量信号
$ x\left(t\right) $ ，其HMC被定义为$$ H\left(t,f,S \left(t\right)\right)={\int }_{-\infty }^{+\infty }x\left(t\right){h}_{T}\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{{\text{π}} }\left(ft+S \left(t\right)\right))\mathrm{d}t $$ (1) 式中：t，f分别为时间和频率；
$ S\left(t\right)$ 为瞬时频率的解调函数；${h}_{T}\left(t\right) $ 为窗函数，其中心为$ \tau $ 、宽度为T，为了便于区分信号中的谐波分量，选择具有低混淆特性的汉宁窗。对式（1）进一步变形，可得
$$\begin{split} & H\left(t,f,S \left(t\right)\right) ={\int }_{-\infty }^{+\infty }x\left(t\right){h}_{T}\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} \left(ft+S \left( t\right)\right))\mathrm{d}t =\\& \qquad \;\;\; {\int }_{-\infty }^{+\infty }\left(x\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} S \left( t\right))\right){h}_{T}\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} ft)\mathrm{d}t = \\& \;\;\; \qquad {\int }_{-\infty }^{+\infty }\widetilde{x}\left(t\right){h}_{T}\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} ft)\mathrm{d}t \end{split} $$ (2) 式中
$ \widetilde{x}\left(t\right) $ 为解调后的信号。在HMC计算过程中，对于有限能量信号
$ x\left(t\right) $ ，先通过STFT对瞬时频率进行粗略估计，之后采用泰勒公式将粗略估计的瞬时频率$ f\left(t\right) $ 展开：$$\begin{split} f\left(t\right)= &f\left(\tau \right)+\frac{{f}^{{'}}\left(\tau \right)}{1!}\left(t-\tau \right) +\frac{{f}^{{'}{'}}\left(\tau \right)}{2!}{\left(t-\tau \right)}^{2}+\cdots +\\ & \frac{{f}^{\left(n\right)}\left(\tau \right)}{n!}{\left(t-\tau \right)}^{n}+{R}_{n}\left(t\right) \end{split}$$ (3) 式中：n为阶数；
$ {R}_{n}\left(t\right) $ 为泰勒余项。在式（3）中，余项的大小取决于余项中t的阶次。当t处于高阶次时，余项值不断减小，同时无限逼近瞬时频率
$ f\left(t\right) $ 。因此，可以用关于t的负指数幂的形式来近似余项，同时通过调节参数c实现对瞬时频率的匹配：$$f\left(t\right)\approx {f}_{0}+c{t}^{-d} $$ (4) 式中：
$ {f}_{0} $ 为幂指数函数的常数项；d为指数因子。由式（4）可知，粗略估计出的瞬时频率曲线为指数幂形式。因此，瞬时频率的解调函数
$ S\left(t\right) $ 可以被定义为$$ \begin{split} S \left(t\right)= & {\int }_{-\infty }^{+\infty }-f\left(t\right)\mathrm{d}t ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}-\left({f}_{0}+c{t}^{-d}\right)\mathrm{d}t = \\& -\left({f}_{0}t+\frac{c}{1-d}{t}^{1-d}\right) \end{split}$$ (5) 则式（2）中解调操作因子
$ \mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2\mathrm{{\text{π}} }S \left(t\right)) $ 可表示为$$\begin{split} \mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2\mathrm{{\text{π}} }S \left(t\right)) =& \mathrm{e}\mathrm{x}\mathrm{p}\left( { -\mathrm{j}2\mathrm{{\text{π}} }-\left({f}_{0}t+\frac{c}{1-d}{t}^{1-d}\right) } \right) = \\& \mathrm{e}\mathrm{x}\mathrm{p}\left(\mathrm{j}2\mathrm{{\text{π}} }\left({f}_{0}t+\frac{c}{1-d}{t}^{1-d}\right)\right) \end{split}$$ (6) 为了方便计算，d可设定为0.5。对于
$ {f}_{0} $ 和c，可通过将瞬时频率曲线上任意2个时频点$ \left({t}_{1}，{f}_{1}\right) $ 和$ \left({t}_{2}，{f}_{2}\right) $ 代入式（5）进行求解。因此，可在每个汉宁窗中，分别获得相应的解调函数$ S \left(t\right) $ 和解调操作因子$ \mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} S \left(t\right)) $ 。将解调函数$ S \left(t\right) $ 和解调操作因子$ \mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{j}2{\text{π}} S \left(t\right)) $ 分别转换成向量形式$ \overline {{{\boldsymbol{E}}}} $ 和$ \overline {{{\boldsymbol{X}}}} $ 。因此，经过HMC变换解调后的信号为$$ \widetilde {x}\left(t\right)=\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\left[\overline {{\boldsymbol{E}}} \cdot \overline {{\boldsymbol{X}}}\right] $$ (7) 式中
$\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}\left[ \cdot \right]$ 为实数运算操作。将
$ \widetilde {x}\left(t\right) $ 代入式（2），可实现对瞬时频率的估计。1.2 基于Vold-Kalman滤波的谐波分量提取
Vold-Kalman滤波器是一种可有效跟踪信号波动变化的时变滤波器，能跟随信号特性自适应分离和提取谐波[16-17]。相对于传统的带通滤波器，Vold-Kalman滤波器的中心带宽可以跟随转速的波动自适应调整，这种性质使其很适用于对煤矿机械设备轴承信号的跟踪滤波。在提取第k次谐波分量的同时，为有效抑制其他相邻谐波分量，Vold-Kalman滤波器的瞬时带宽
$ {C}_{k} $ 需满足如下条件：$$ {C}_{k}\leqslant 0.5{O}_{k} $$ (8) 式中
$ {O}_{k} $ 为第k次谐波和其相邻谐波之间的距离。1.3 瞬时相位计算
当第k次谐波分量
$ e\left(n\right) $ 的时域信号从原始振动信号中被提取出来后，采用Hilbert变换计算第k次谐波的瞬时相位：$$ {\varphi }_{k}\left(n\right)=\mathrm{u}\mathrm{n}\mathrm{w}\mathrm{r}\mathrm{a}\mathrm{p}\left[\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\frac{\overline {e}\left(n\right)}{e\left(n\right)}\right] $$ (9) 式中：
$ \mathrm{u}\mathrm{n}\mathrm{w}\mathrm{r}\mathrm{a}\mathrm{p}\left[\cdot \right] $ 为相位解卷积操作，可将$ e\left(n\right) $ 的瞬时相位从区间$ \left[-{\text{π}} ，{\text{π}} \right] $ 映射到相位累积空间；$ \overline {e}\left(n\right) $ 为$ e\left(n\right) $ 经Hilbert变换后的结果。理论上，第k次谐波信号的瞬时相位
$ {\varphi }_{k}\left(n\right) $ 与原始信号瞬时相位$ \varphi \left(n\right) $ 之间严格遵循线性比例关系。但信号在实际的传递过程中，受振动传递路径的影响，瞬时相位会发生偏移。因此，式（9）可修正为$$ {\varphi }_{k}\left(n\right)=a\varphi \left(n\right)+{\varphi }_{{\rm{s}}}\left(n\right) $$ (10) 式中：a为
$ {\varphi }_{k}\left(n\right) $ 和$ \varphi \left(n\right) $ 之间的线性比例系数；$ {\varphi }_{\mathrm{s}}\left(n\right) $ 为由振动传递路径引入的相位偏移。由于振动传递路径引入的相位偏移较大，需要对相位进行修正。修正后的实际瞬时相位为
$${\widetilde{\varphi }\left(n\right)=\varphi }_{k}\left(n\right)/a=\varphi \left(n\right)+{\varphi }_{{\rm{s}}}\left(n\right)/a $$ (11) 1.4 信号角度域重采样
对估计出的瞬时相位
$\widetilde{\varphi }\left(n\right) $ 进行反函数运算，可建立时间域和角度域的映射关系：$$ {t\,}_{n}^{k}={\widetilde{\varphi }}^{-1}\left(k\Delta \theta \right) $$ (12) 式中：
$ {t\,}_{n}^{k} $ 为第k次谐波的时间信息；$ \Delta \theta $ 为等间隔的角度域增量。在角度域重采样过程中，为了避免产生频率混淆，
$ \Delta \theta $ 需要满足如下约束：$$ \Delta \theta \leqslant \frac{360 \;\mathrm{m}\mathrm{i}\mathrm{n}\left\{f\left(t\right)\right\}}{{f}_{\mathrm{s}}} $$ (13) 式中
$ {f}_{\mathrm{s}} $ 为信号采样频率。通过时间域和角度域的映射关系，以
$ \Delta \theta $ 为采样间隔，可实现原始时间域信号在角度域的等角度重采样，从而获得角度域重采样信号。2. 仿真验证
根据煤矿机械设备轴承的实际瞬态非平稳运行工况，设置轴承振动仿真信号[18-19]：
$$ y\left(t\right)=\sum _{i}{A}_{i}s\left(t-{t}_{i}\right)+\sum _{k}{B}_{k}\mathrm{cos}\left(2{{\text{π}} }kf\left(t\right)+{\varphi }_{k}\right)+g\left(t\right) $$ (14) 式中：
$ \displaystyle \sum\limits _{i}{A}_{i}s\left(t-{t}_{i}\right) $ 为由轴承故障激发的脉冲序列，$ {A}_{i} $ 和$ {t}_{i} $ 分别为第$ i $ 次脉冲序列的幅值和激发时间；$ \displaystyle \sum\limits _{k}{B}_{k}\mathrm{c}\mathrm{o}\mathrm{s}\left(2{\text{π}} kf\left(t\right)+{\varphi }_{k}\right) $ 为由偏心、不对中、失衡等引起的转频振动等谐波分量，$ {B}_{k} $ 和$ {\varphi }_{k} $ 分别为第k次谐波分量的幅值和初始相位；$ g\left(t\right) $ 为噪声干扰信号。假设轴承外圈固定在轴承座中，内圈随转轴一起旋转，且在轴承外圈上存在1处局部剥落缺陷。因此，轴承的故障脉冲信号
$ s\left(t\right) $ 可设置为[19]$$ s\left(t\right)=\mathrm{e}\mathrm{x}\mathrm{p}\left(-500t\right)\mathrm{s}\mathrm{i}\mathrm{n}\left(4\;000{\text{π}} t\right) $$ (15) 假设轴承故障信号中包含2个关于转频的谐波分量，其幅值分别为
$ {B}_{1}=0.005g $ （g为重力加速度），$ {B}_{2}=0.01g $ ，初始相位分别为$ {\varphi }_{1}={\text{π}} /6 $ ，$ {\varphi }_{2}=-{\text{π}} /3 $ 。在测试过程中轴承经历了剧烈的转速上升和转速下降过程，因此瞬时频率[18]为$$ f\left(t\right)=\left(500+1\;000\mathrm{s}\mathrm{i}\mathrm{n}\left(0.5\mathrm{{\text{π}} }t\right)\right)/60 $$ (16) 将轴承故障特征频率对外圈转频归一化处理[20]，设轴承的外圈故障特征频率为转轴转频的4.35倍，则故障脉冲的平均角度间隔为360°/4.35≈82.76°。设置信号的采样频率为20 kHz，采样持续时间为2 s，噪声干扰为−3 dB的白噪声。
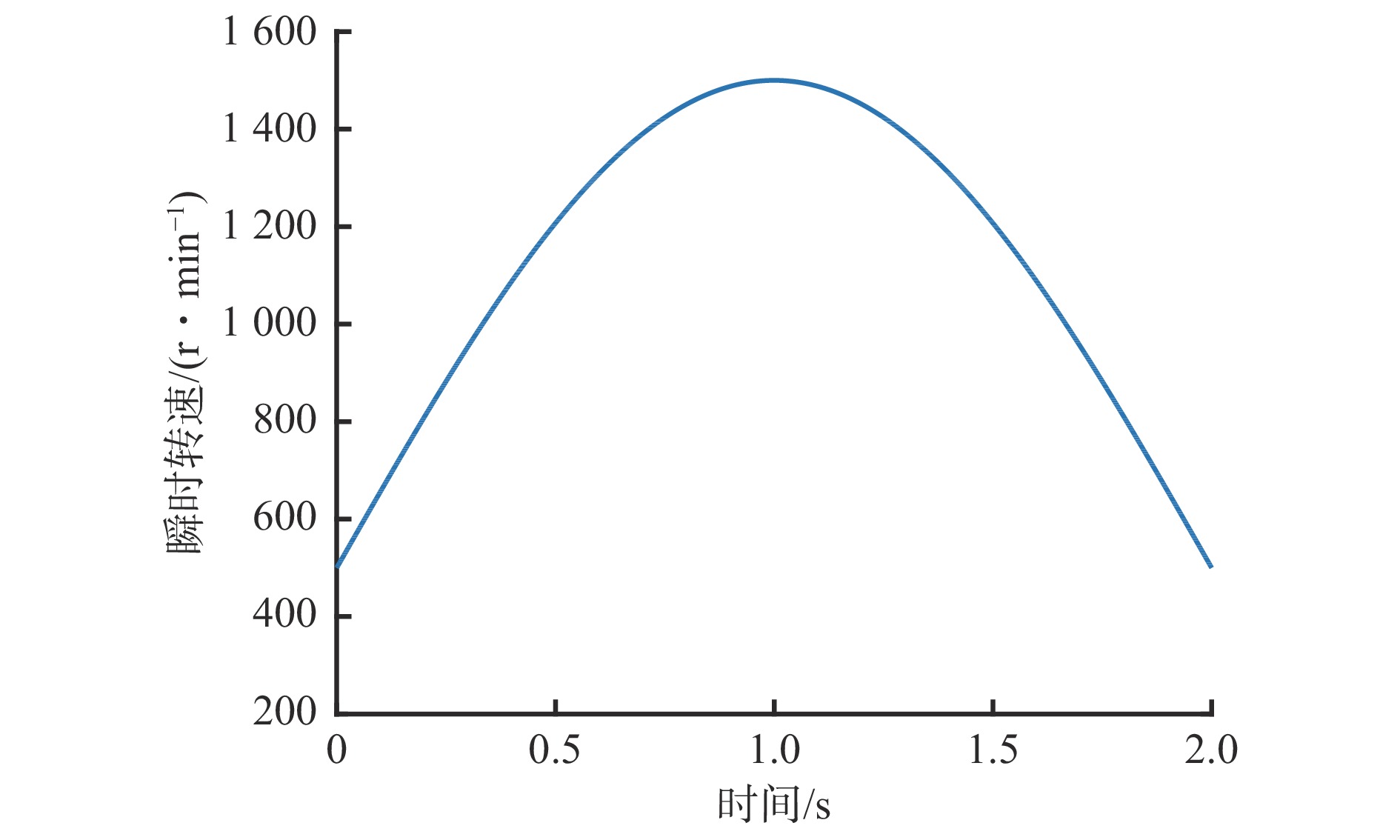
轴承瞬时转速模拟曲线如图2所示，可模拟煤矿机械设备作业过程中转速剧烈波动工况。
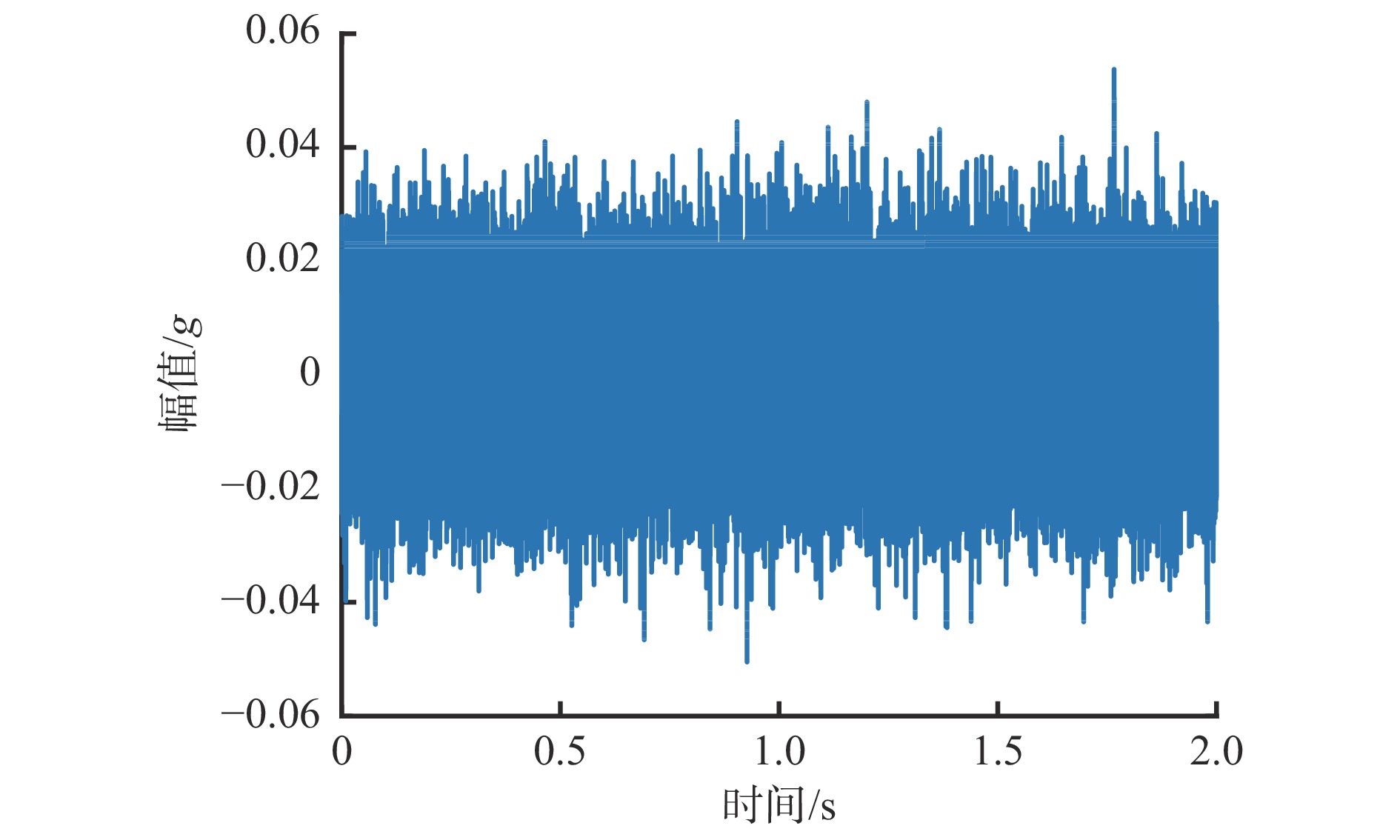
仿真信号的时域波形如图3所示。由于转速剧烈波动，各谐波分量及噪声干扰混淆，难以发现由轴承缺陷所激发的故障冲击特征。此外，受轴承转速剧烈波动影响，传统的时域和频域统计指标分析不再适用。
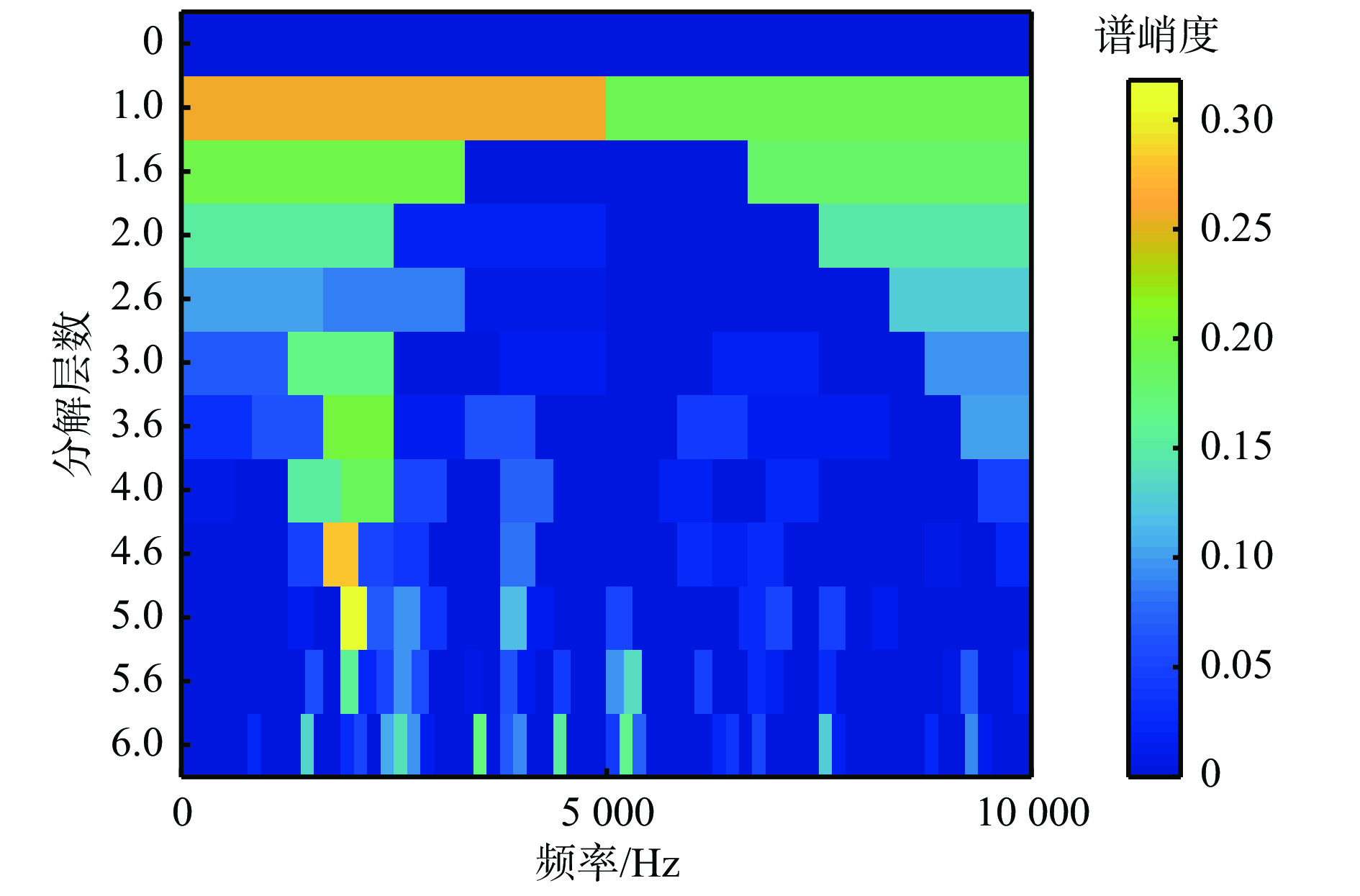
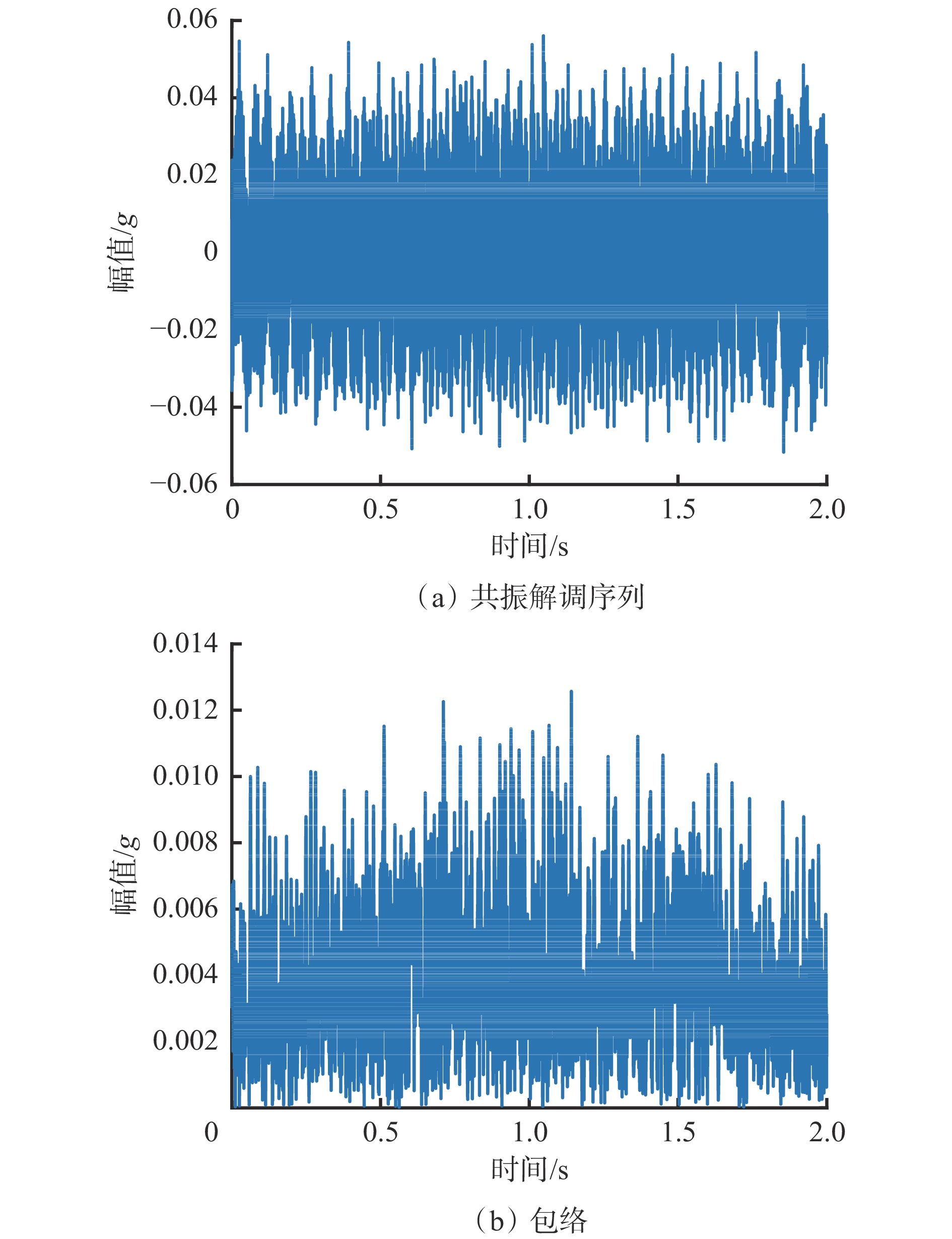
采用本文方法对仿真信号进行处理。首先，通过快速谱峭度分析法[21]获得仿真信号的谱峭度，如图4所示，进而识别出轴承的最佳共振频带。然后，根据最佳共振频带设计中心频率为1 875 Hz、带宽为416.67 Hz的带通滤波器，提取出仿真信号的共振解调序列，如图5（a）所示。最后，采用Hilbert变换得到仿真信号的包络，如图5（b）所示。
![]()
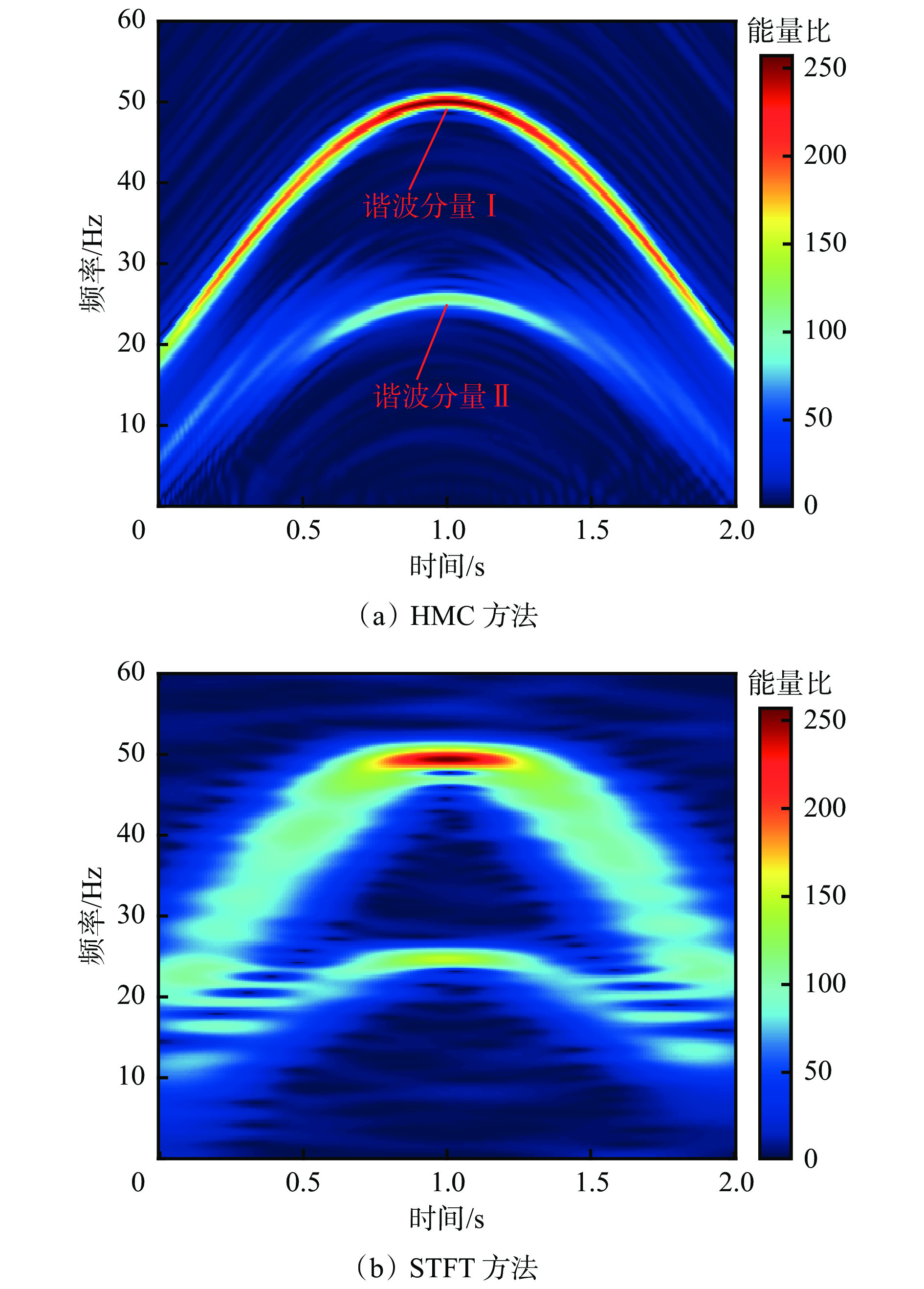
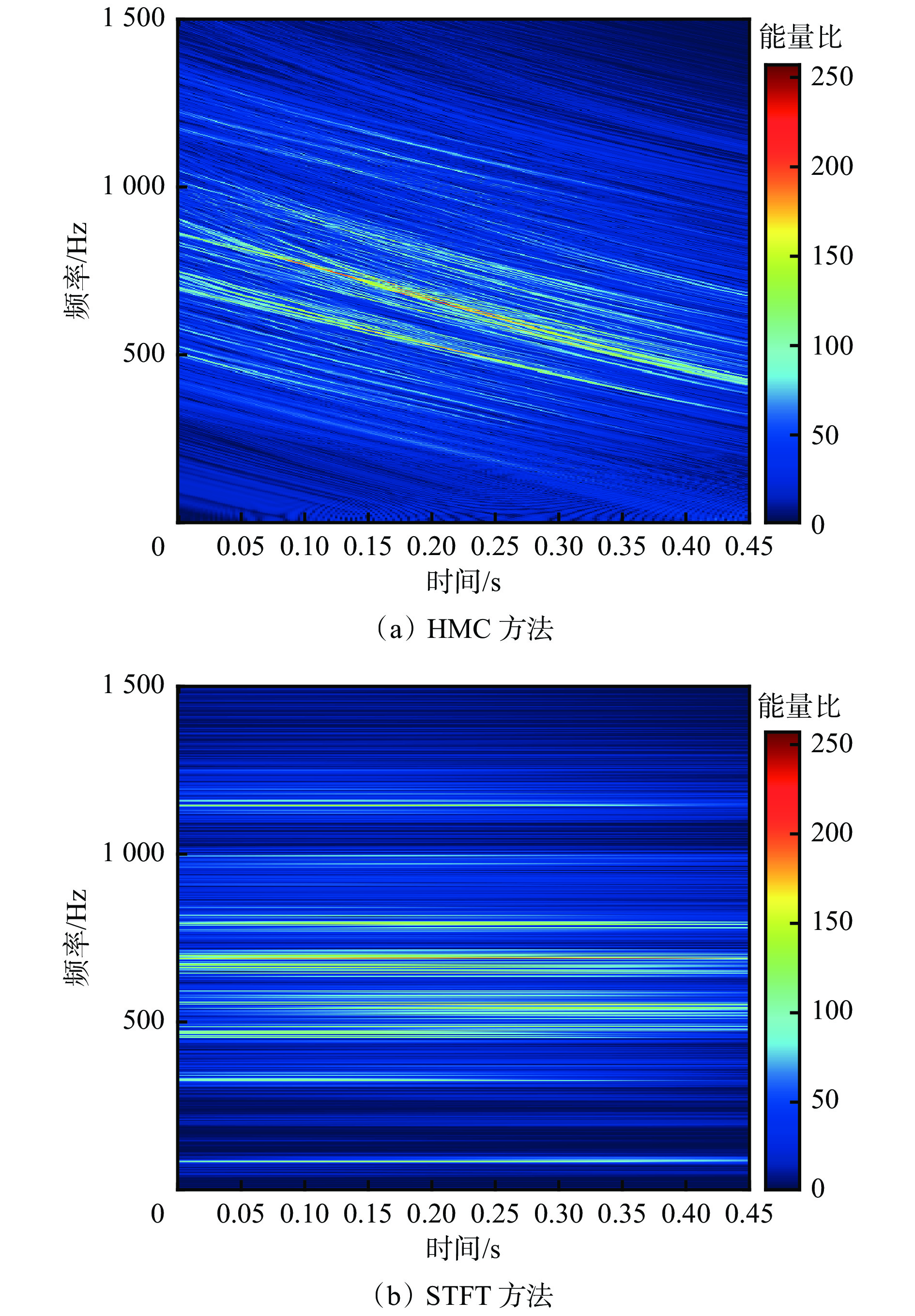
图 5 仿真信号的共振解调序列和包络Figure 5. Resonance demodulation sequence and envelope of simulated signal为验证基于HMC的时频分析方法在转速剧烈波动工况下对瞬时频率估计的有效性，分别采用HMC方法和STFT方法对瞬时频率进行估计，得到的时频谱如图6所示。可看出采用HMC方法得到的时频谱中时频聚集性显著且分辨率高，而采用STFT方法得到的时频谱在剧烈转速波动和噪声双重干扰下较模糊，且时频聚集性和分辨率较差。
![]()
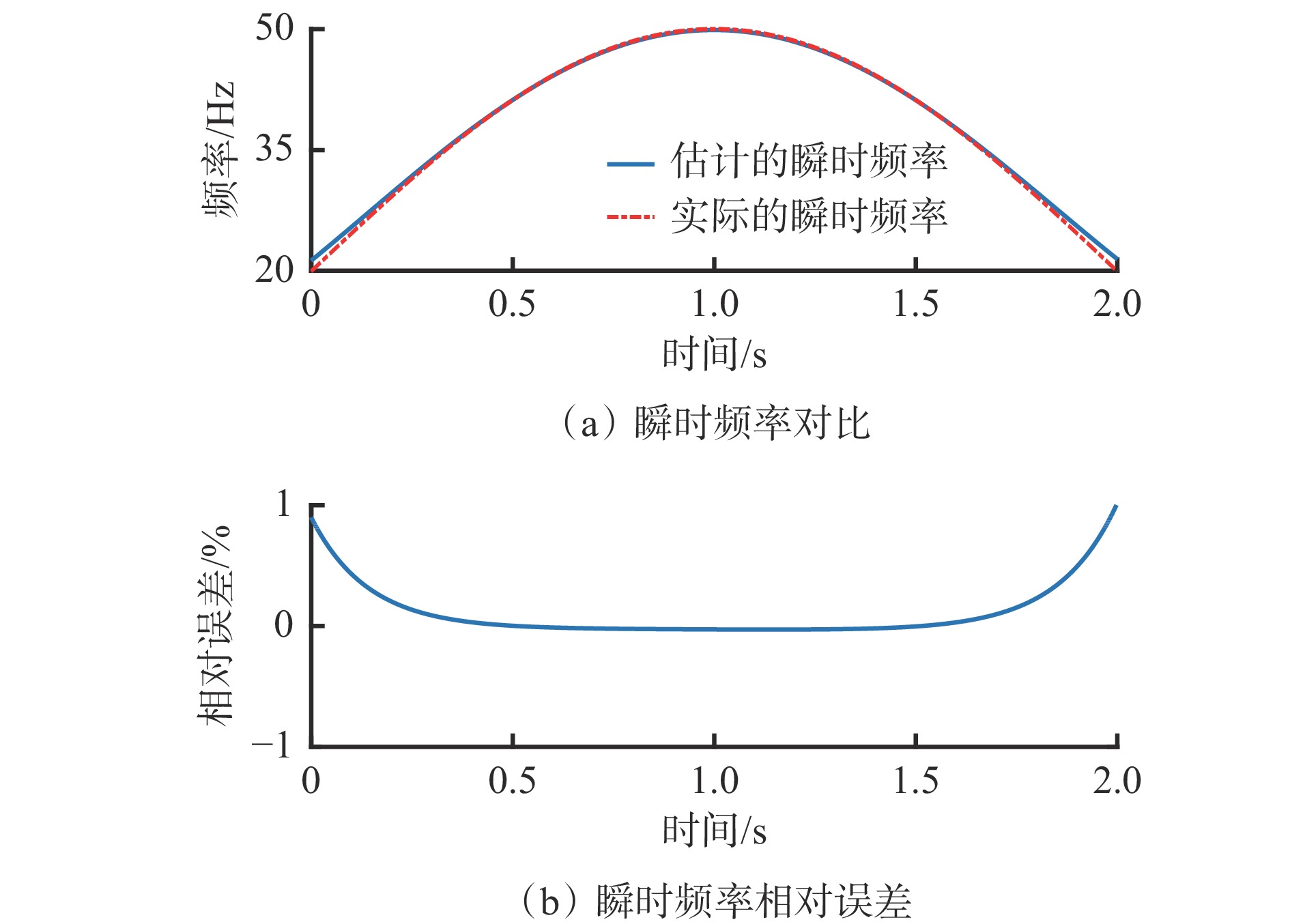
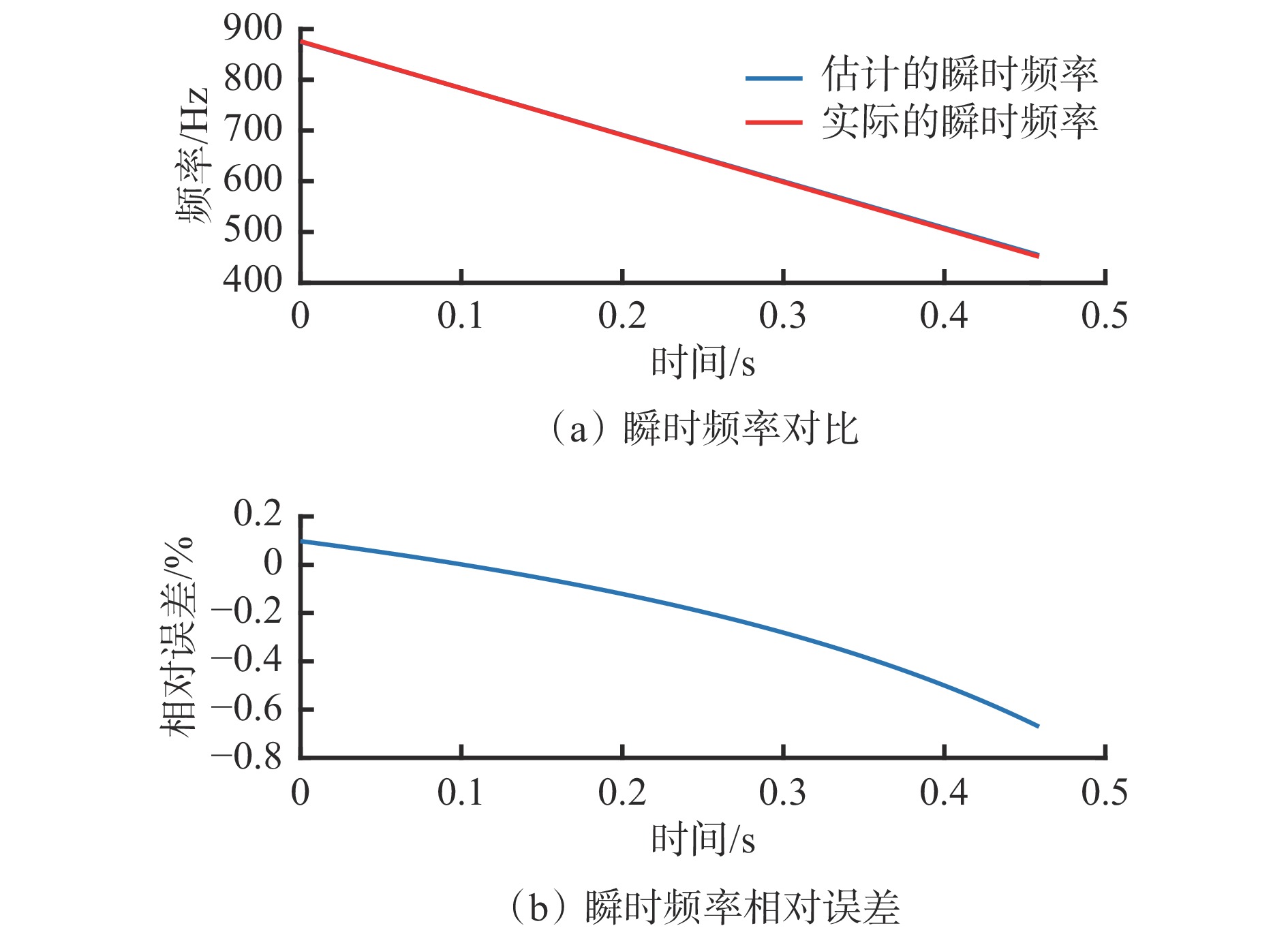
图 6 不同方法下仿真信号时频谱Figure 6. Time-frequency spectrum of simulated signal under different methods图6（a）中有2个能量突出的谐波分量，对谐波分量Ⅰ进行瞬时频率估计，结果如图7所示。可看出估计的瞬时频率曲线与实际的瞬时频率曲线（通过式（16）计算所得）高度重合，瞬时频率估计值与实际值之间的最大相对误差不超过1%。
![]()
图 7 仿真信号瞬时频率估计结果Figure 7. Instantaneous frequency estimation result of simulated signal以HMC方法精确估计出的瞬时频率为中心频率，利用Vold-Kalman滤波器对谐波分量Ⅱ进行自适应提取，结果如图8所示。
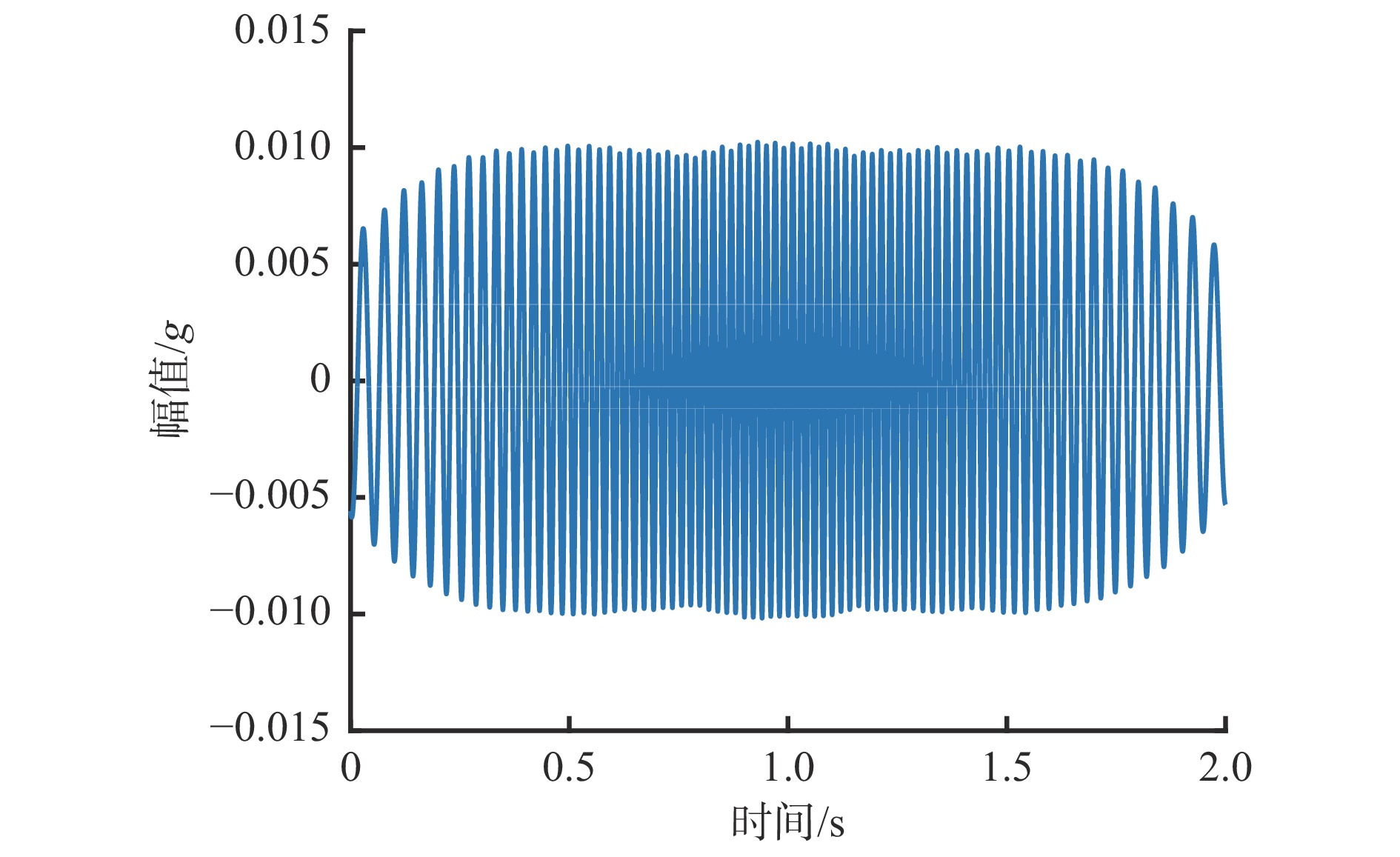
从图8可看，出提取出的谐波分量波形平滑，幅值为0.01 g，与设置的仿真信号幅值
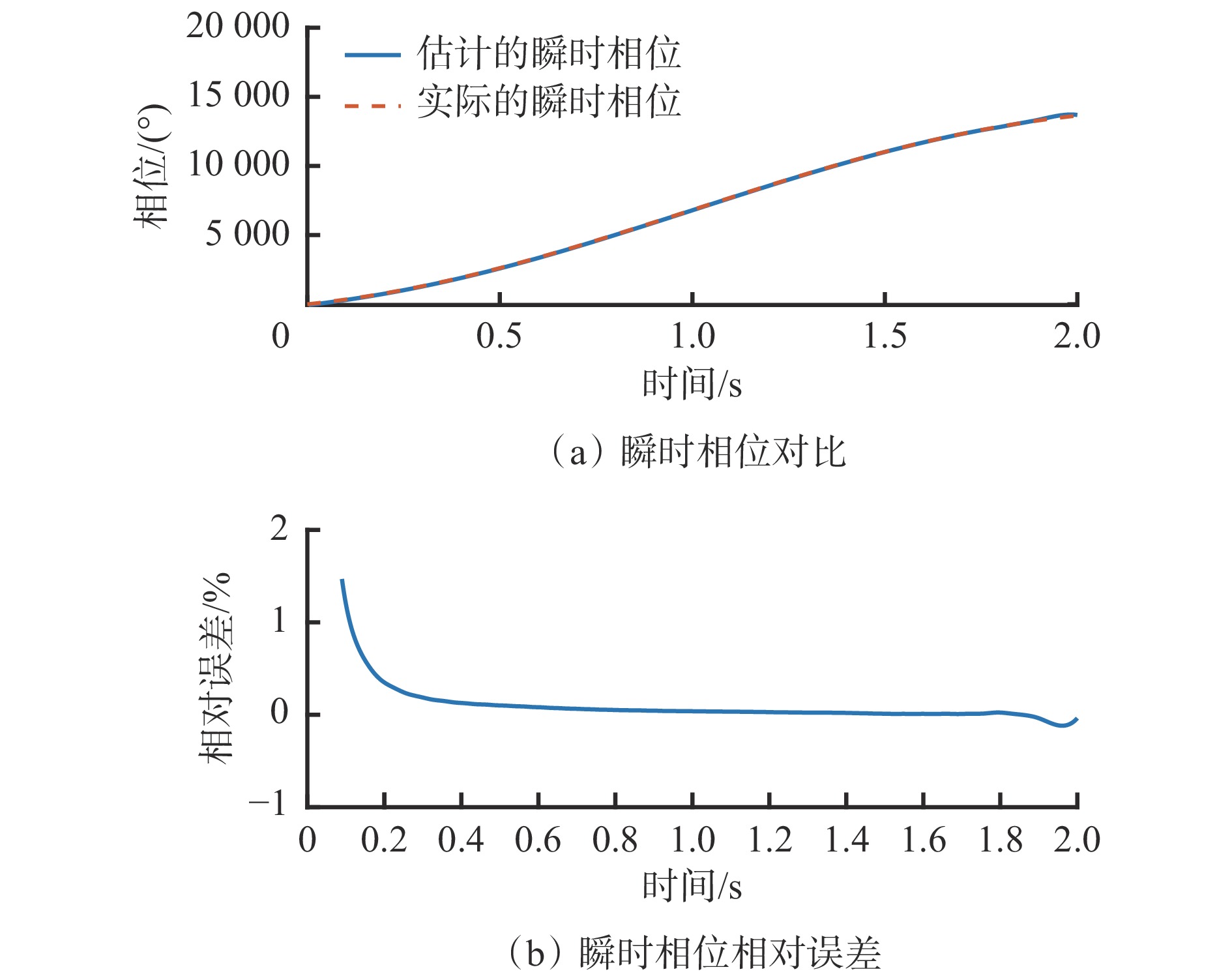
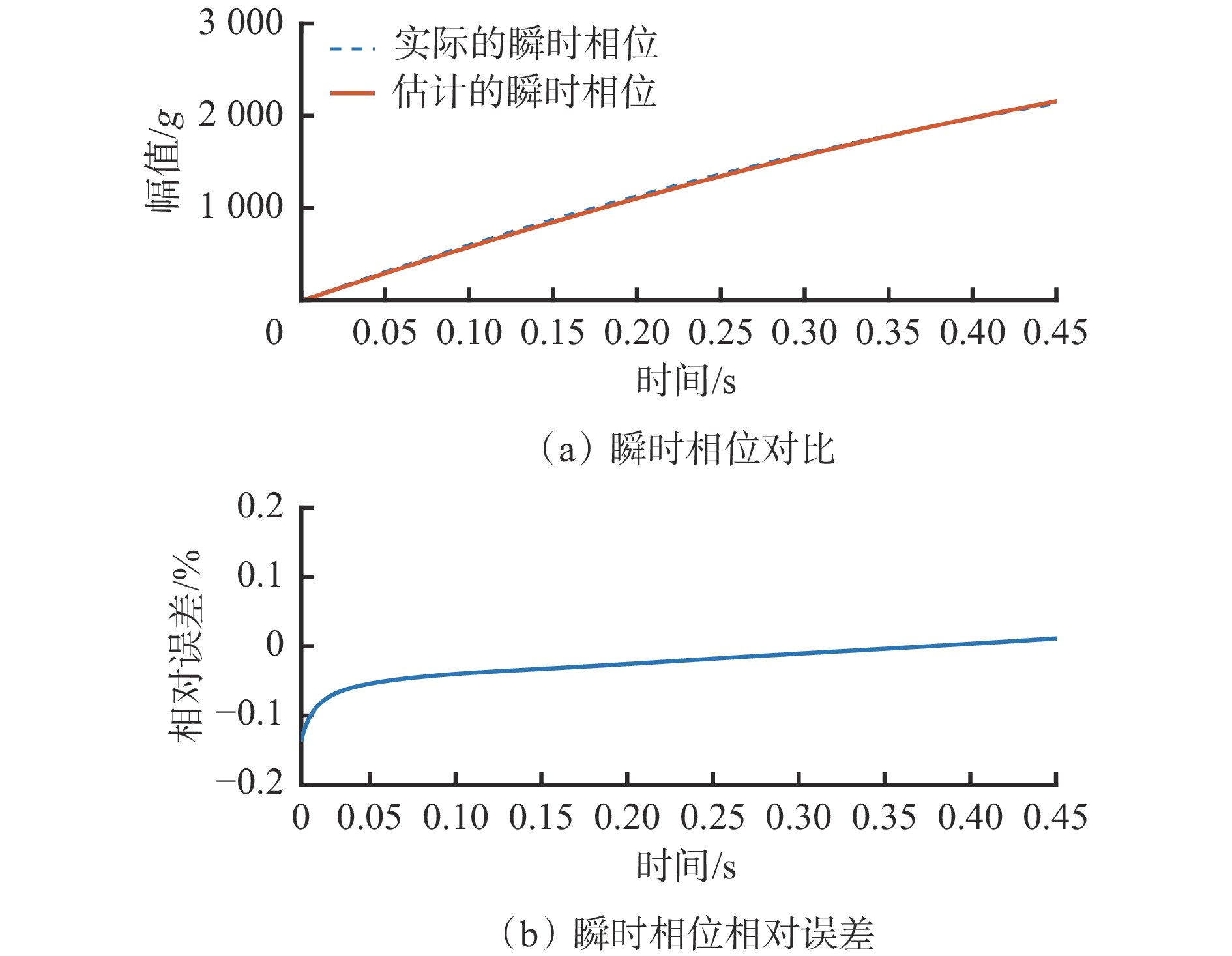
$ {B}_{2}=0.01 \; g $ 相同。根据式（8），取Vold-Kalman滤波器的瞬时带宽为$ 0.5 $ 阶次。![]()
图 8 Vold-Kalman滤波器提取的谐波分量Figure 8. Harmonic components extracted by Vold-Kalman filter依据式（9）和式（11），估计出瞬时相位，并与实际瞬时相位对比，结果如图9所示。可看出估计的瞬时相位曲线与实际瞬时相位曲线高度重合，瞬时相位估计值与实际值的最大相对误差不超过2%。
根据估计出的瞬时相位，通过式（12）获得时间域和角度域的映射关系，进而完成角度域的重采样。再将重采样的角度域信号进行快速傅里叶变换，得到包络阶次谱，如图10所示。可看出本文方法和有键相阶次跟踪方法得到的包络阶次谱高度吻合，通过本文方法可清晰找到轴承外圈故障特征阶次（4.35阶次）及相关倍频特征阶次，证明轴承外圈存在故障。
3. 试验验证
为验证本文方法对煤矿机械设备轴承故障诊断的有效性，搭建轴承模拟试验系统，如图11所示。
将轴承外圈通过过盈配合固定于轴承座内，轴承内圈与轴一起旋转。电动机与伺服驱动系统提供动力输入，驱动轴承转动。采用3个灵敏度为50 mV/g的单轴振动加速度传感器采集轴承振动信号。转速计为光电脉冲编码器，用来采集轴承转频信息。信号采集系统主要设备为Coco−80数字采集仪。为了模拟煤矿机械设备运行时轴承运行工况，设置轴承经历瞬间启动、载荷及转速迅速上升和瞬间停止3个过程。设置采样频率为25.6 kHz。
轴承几何参数见表1。试验设置轴承外圈存在人为设置的磨损故障缺陷，如图12所示。
表 1 轴承几何参数Table 1. Bearing geometry parameters滚动体直径/mm 节圆半径/mm 接触角/（°） 滚动体个数 6 25 15 8 通过归一化操作[20]可得轴承外圈故障特征阶次：
$$ {F}_{\mathrm{B}\mathrm{P}\mathrm{F}\mathrm{O}}=\frac{{\textit{z}}{f}_{{\rm{r}}}}{2}\left(1-\frac{r}{D}\mathrm{c}\mathrm{o}\mathrm{s} \; \phi \right) $$ (17) 式中：z为滚动体个数；fr为外圈转频；r为节圆半径；D为滚动体直径；
$ \phi $ 为接触角。将表1数据代入式（17），计算出轴承外圈故障特征阶次为3.072 7。
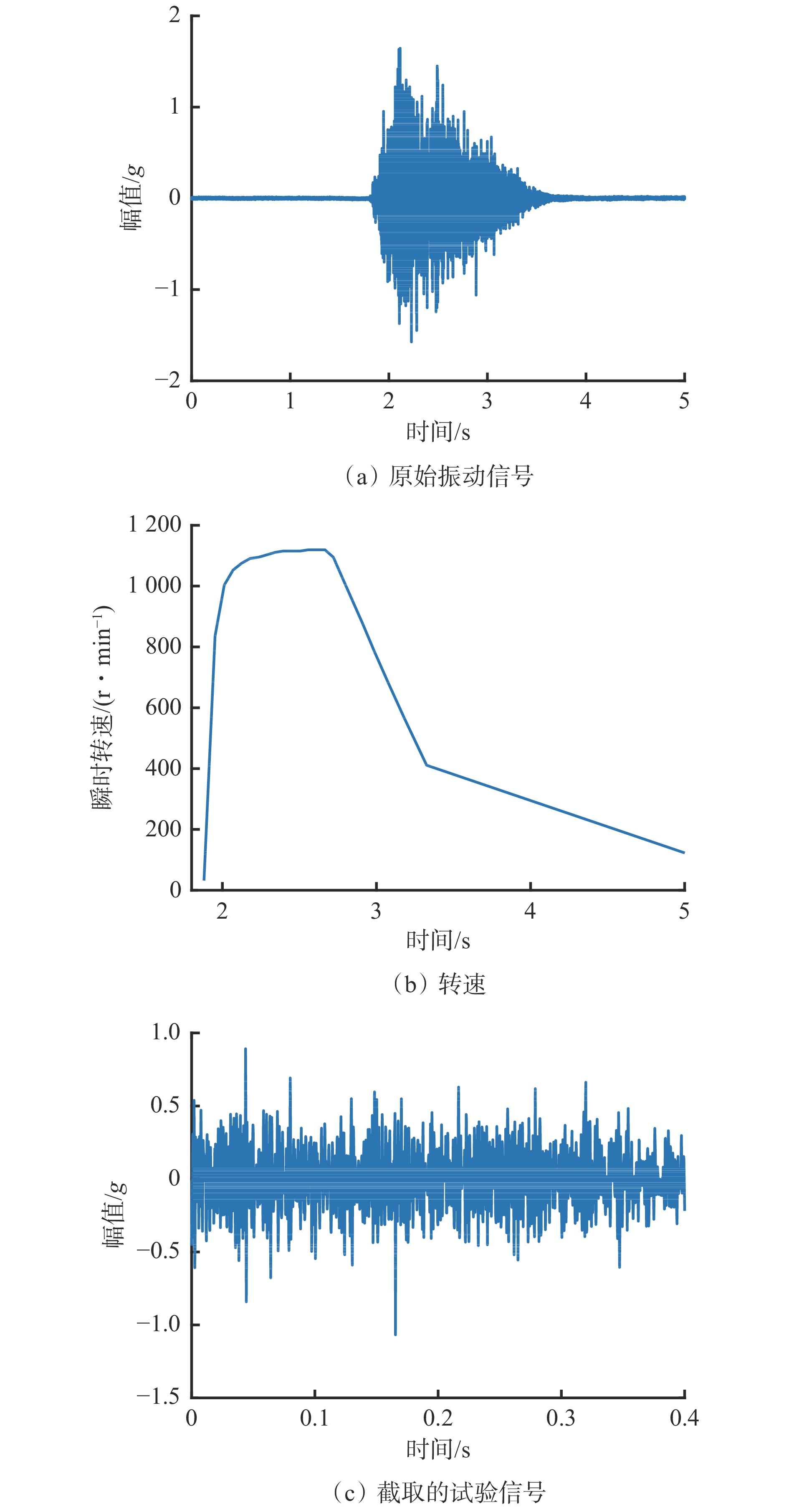
采集的原始振动信号、转速和截取的试验信号如图13所示。由于转速的剧烈瞬态波动，从图13（a）和图13（c）中无法识别出任何关于轴承故障的冲击特征。
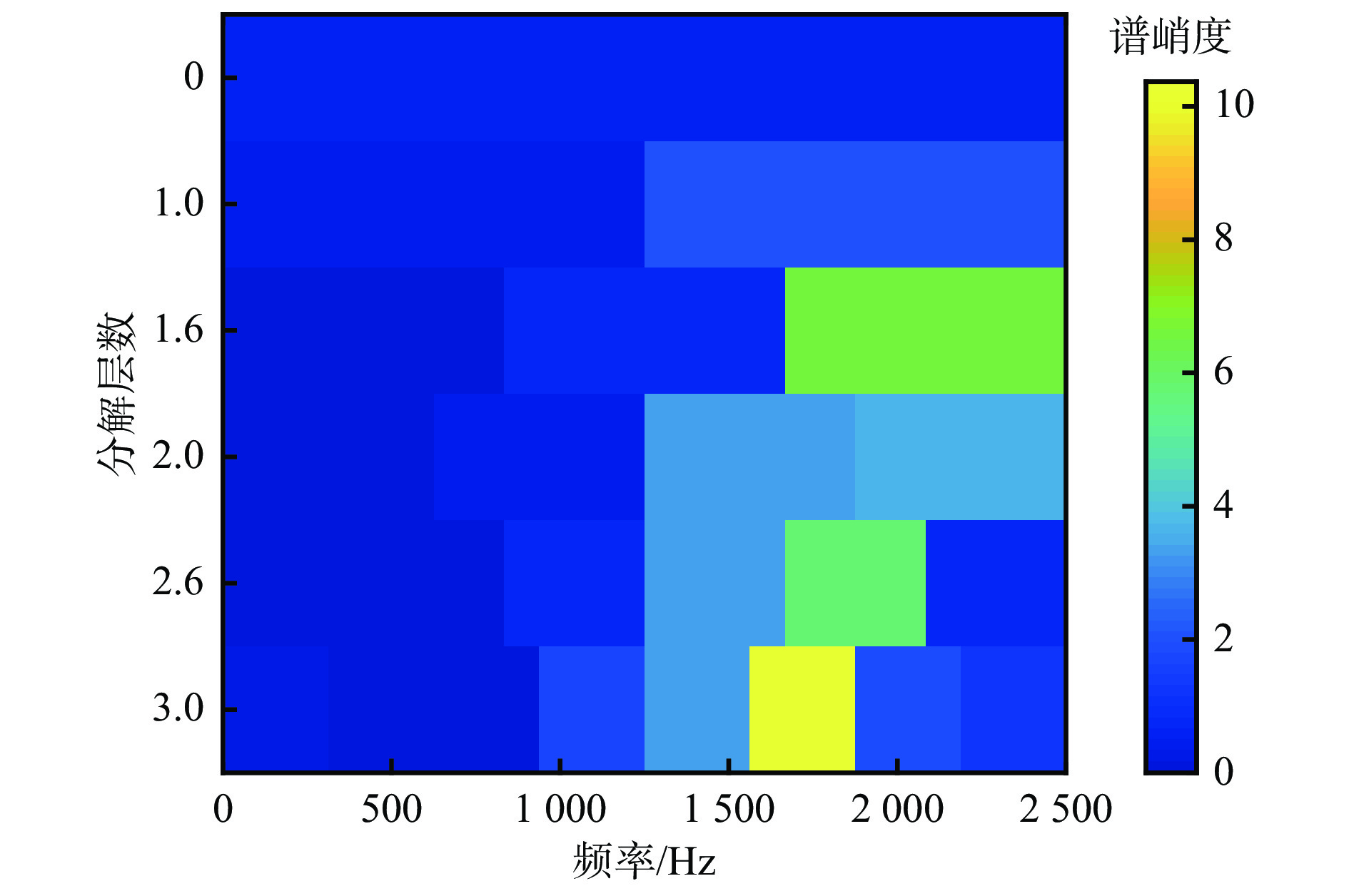
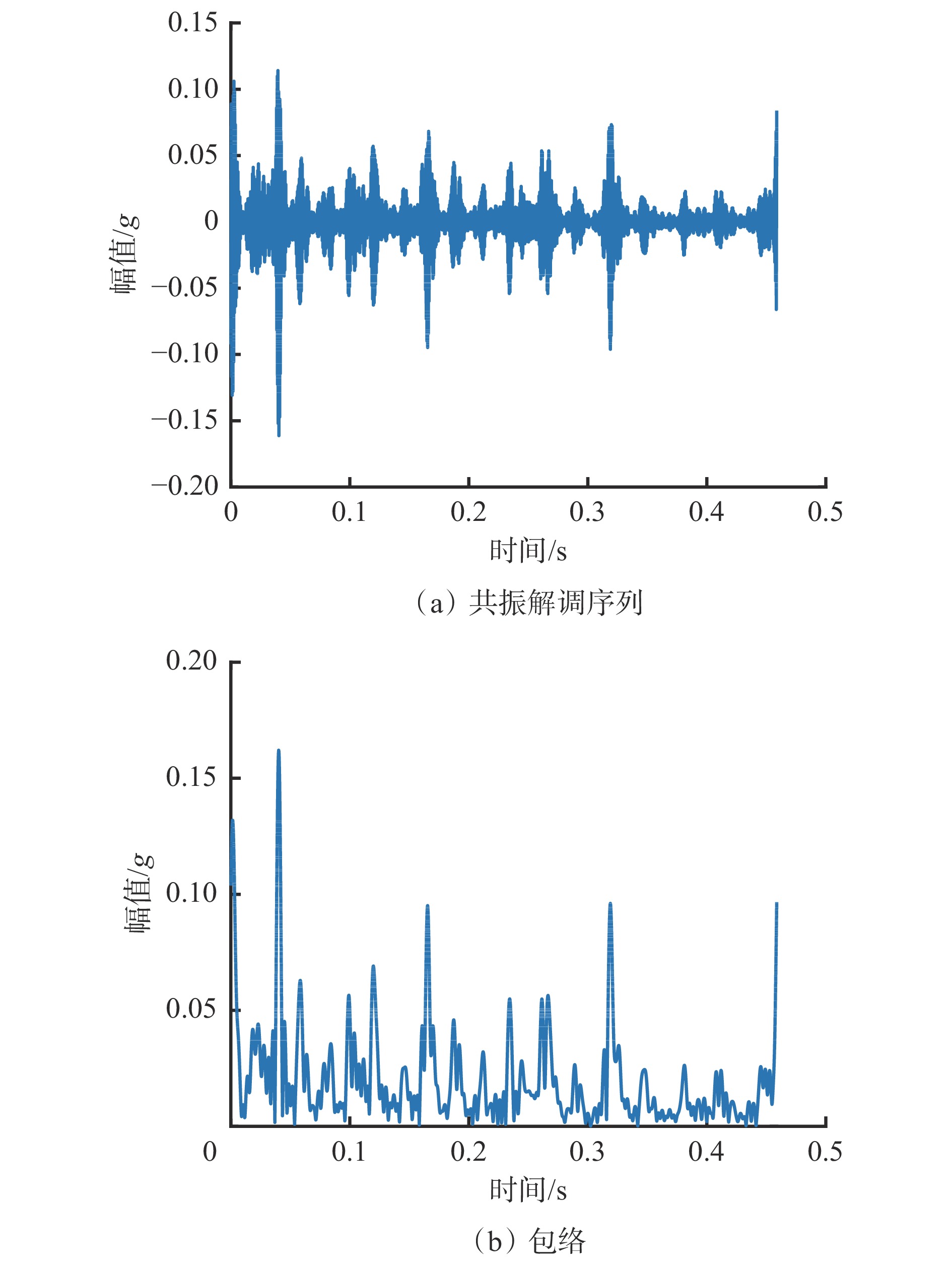
通过快速谱峭度分析法获得截取的试验信号的谱峭度，如图14所示，进而可识别出轴承的最佳共振频带。根据获得的最佳共振频带设计中心频率为1 718.8 Hz、带宽为312.5 Hz的带通滤波器，进而提取出截取的试验信号的共振解调序列，并采用Hilbert变换得到截取的试验信号的包络，如图15所示。
![]()
图 15 试验信号的共振解调序列和包络Figure 15. Resonance demodulation sequence and envelope of test signal分别采用HMC方法和STFT方法处理试验信号，得到时频谱，如图16所示。可看出采用STFT方法处理后的时频谱中识别不出任何频率波动的趋势，而由于HMC方法在瞬态条件下的优异性能，可清楚识别出瞬时频率的变化趋势。
![]()
图 16 不同方法下试验信号时频谱Figure 16. Time-frequency spectrum of test signal under different methods图16（a）中有2个谐波能量较为显著。为了确定这2个谐波分量的位置，在0.058 38 s处对其进行检测，其中心频率分别为 975.3 Hz和953.6 Hz，表明2个谐波分量之间的频率间隔为21.7 Hz。因此，确定2个谐波分量分别为试验信号的第45（975.3 Hz/21.7 Hz≈45）个和第44（953.6 Hz/21.7 Hz≈44）个分量。本文通过第45个谐波分量估计试验信号的瞬时频率，结果如图17所示。可看出瞬时频率估计曲线与实际的瞬时频率曲线高度重合，瞬时频率估计值与实际值之间的最大相对误差不超过1%。
采用HMC方法准确估计出瞬时频率后，通过Vold-Kalman滤波器对第45个谐波分量进行自适应提取。根据式（9）和式（10），估计出瞬时相位，并与实际瞬时相位对比，结果如图18所示。可看出估计的瞬时相位曲线与实际的瞬时相位曲线高度重合，瞬时相位估计值与实际值之间的最大相对误差不超过2%。
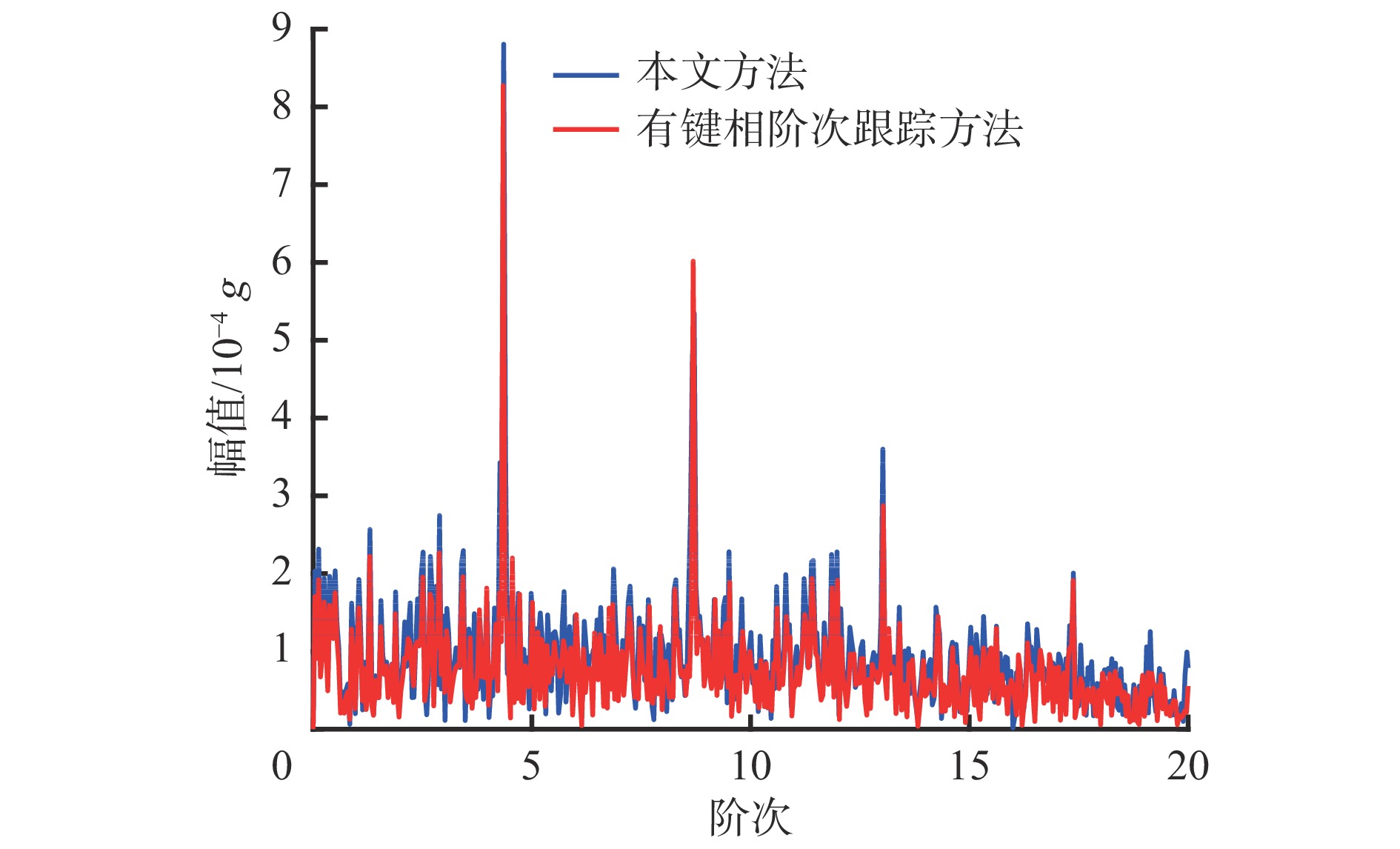
根据估计出的瞬时相位，通过式（12）获得时间域和角度域的映射关系，进而完成角度域重采样。对重采样的包络信号进行快速傅里叶变换，获得包络阶次谱，如图19所示。可看出本文方法和有键相阶次跟踪方法得到的包络阶次谱高度吻合，通过无键相阶次跟踪方法可清晰找到轴承外圈故障特征阶次（3.072 7阶次）及相关倍频特征阶次，由此可明确推断出轴承外圈存在故障。
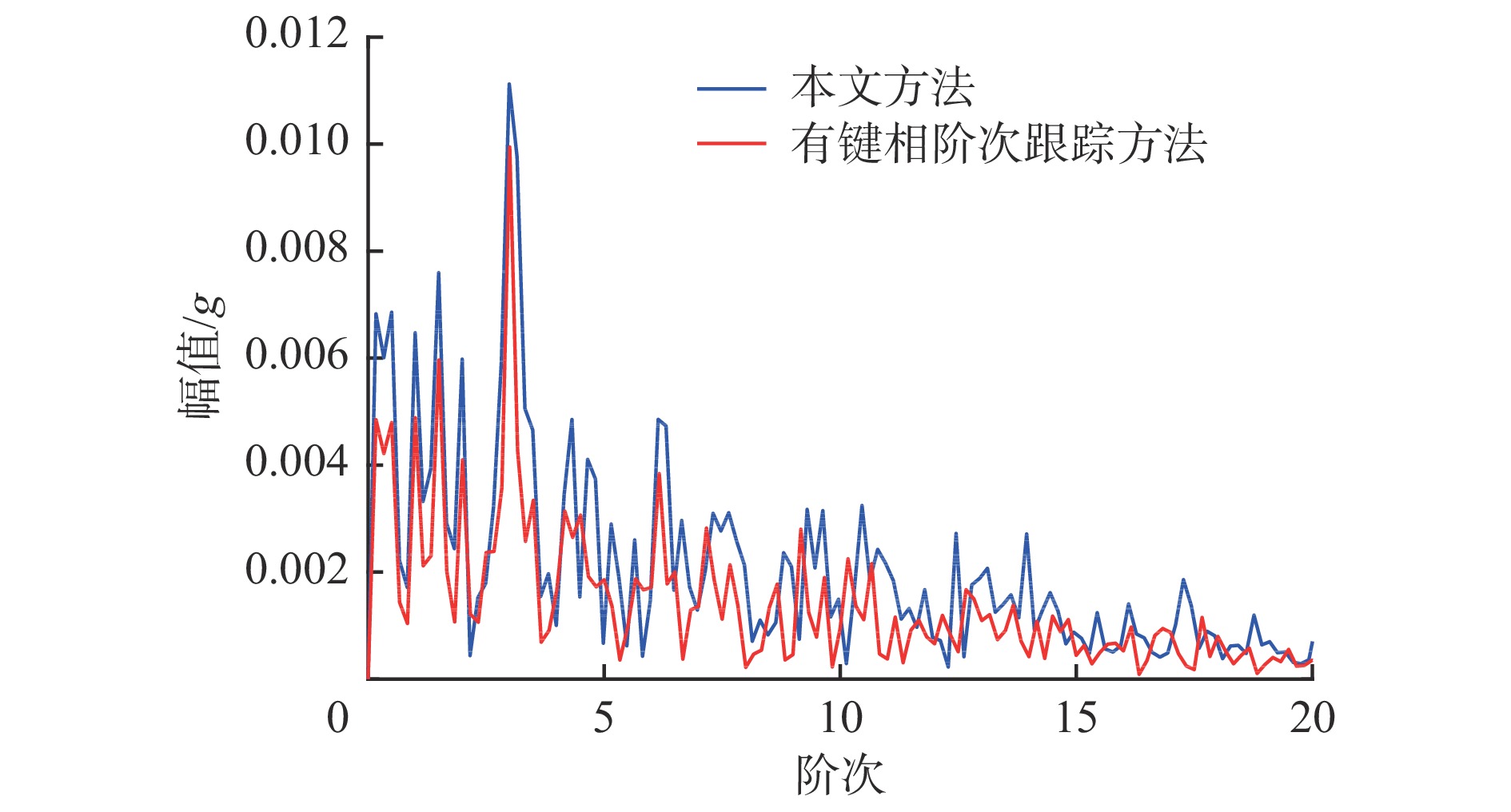
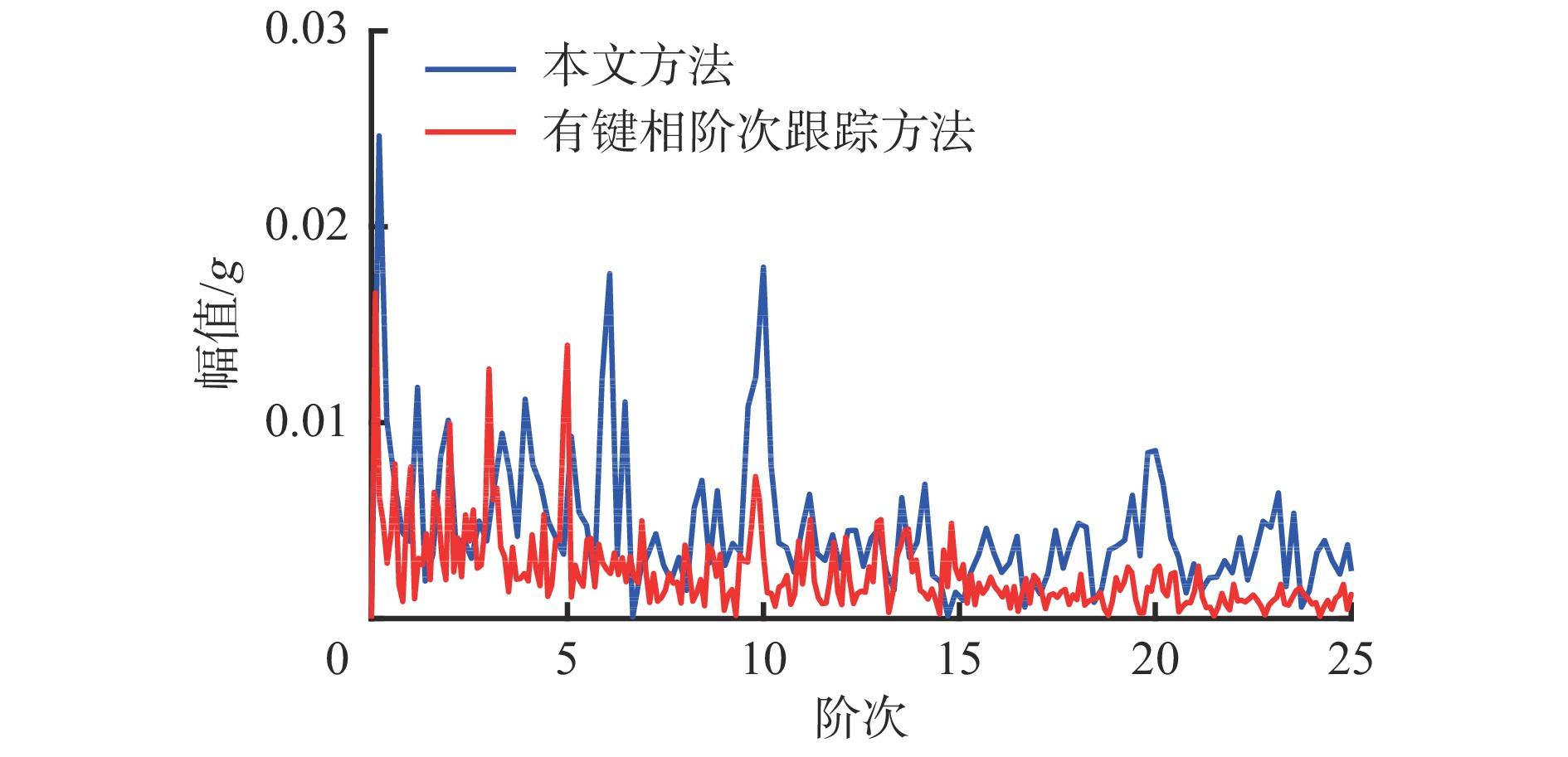
为进一步验证本文方法的有效性，对轴承进行内圈故障加工，如图20所示。应用本文方法得到轴承内圈故障振动信号的包络阶次谱，如图21所示。可看出本文方法和有键相阶次跟踪方法所获得的故障特征阶次相同，但本文方法获得的故障特征阶次幅值明显高于有键相阶次跟踪方法获得的故障特征阶次幅值，更有利于识别故障特征。
![]()
图 21 轴承内圈故障振动信号的包络阶次谱Figure 21. Envelope order spectrum of vibration signal of bearing inner ring fault4. 结论
1） 基于HMC的时频分析方法不依赖传统的局部平稳假设要求，可自适应地匹配调整瞬时频率信号，并对瞬时频率信号进行自适应补偿，进而降低了信号的非线性度，避免了传统基于STFT的时频分析方法在瞬态非平稳运行工况下时频谱模糊的问题，从而精确估计出瞬时频率。
2） 将基于HMC的时频分析方法与无键相阶次跟踪相结合，应用于轴承故障诊断，能够准确估计瞬时频率，获得较为精确的瞬时相位，通过包络阶次谱可准确且明显地表征出轴承故障特征阶次，从而有效识别故障特征。
-
![]()
图 1 基于HMC和无键相阶次跟踪的轴承故障诊断流程
Figure 1. Bearing fault diagnosis process based on harmonic matching compensation and keyless phase order tracking
![]()
图 5 仿真信号的共振解调序列和包络
Figure 5. Resonance demodulation sequence and envelope of simulated signal
![]()
图 6 不同方法下仿真信号时频谱
Figure 6. Time-frequency spectrum of simulated signal under different methods
![]()
图 7 仿真信号瞬时频率估计结果
Figure 7. Instantaneous frequency estimation result of simulated signal
![]()
图 8 Vold-Kalman滤波器提取的谐波分量
Figure 8. Harmonic components extracted by Vold-Kalman filter
![]()
图 15 试验信号的共振解调序列和包络
Figure 15. Resonance demodulation sequence and envelope of test signal
![]()
图 16 不同方法下试验信号时频谱
Figure 16. Time-frequency spectrum of test signal under different methods
![]()
图 21 轴承内圈故障振动信号的包络阶次谱
Figure 21. Envelope order spectrum of vibration signal of bearing inner ring fault
-
[1] 宫涛,杨建华,单振,等. 强噪声背景与变转速工况条件下滚动轴承故障诊断研究[J]. 工矿自动化,2021,47(7):63-71. GONG Tao,YANG Jianhua,SHAN Zhen,et al. Research on rolling bearing fault diagnosis under strong noise background and variable speed working condition[J]. Industry and Mine Automation,2021,47(7):63-71.
[2] 徐青青,赵海芳,李守军. 一种煤矿机械轴承故障诊断方法[J]. 工矿自动化,2019,45(10):80-85,90. XU Qingqing,ZHAO Haifang,LI Shoujun. A fault diagnosis method for coal mine machinery bearing[J]. Industry and Mine Automation,2019,45(10):80-85,90.
[3] 黄海阳,王成,李海波,等. 基于滑动窗变步长等变自适应源分离的线性慢时变结构工作模态参数识别[J]. 计算机集成制造系统,2021,27(1):182-191. HUANG Haiyang,WANG Cheng,LI Haibo,et al. Moving window variable step-size EASI based operational modal parameter identification for slow linear time-varying structure[J]. Computer Integrated Manufacturing Systems,2021,27(1):182-191.
[4] 石博强, 申焱华. 矿用设备时变不确定性分析与寿命预测[M]. 北京: 冶金工业出版社, 2015. SHI Boqiang, SHEN Yanhua. Time-varying uncertainty analysis and life prediction of mining equipment[M]. Beijing: Metallurgical Industry Press, 2015.
[5] WANG K S,HEYNS P S. An empirical re-sampling method on intrinsic mode function to deal with speed variation in machine fault diagnostics[J]. Applied Soft Computing,2011,11(8):5015-5027. DOI: 10.1016/j.asoc.2011.05.056
[6] 吴康福. 基于同步提取变换与阶比分析的轴承变转速故障诊断[J]. 组合机床与自动化加工技术,2021(4):14-18. WU Kangfu. Fault diagnosis of bearing in variable speed based on synchronous extraction transformation and order analysis[J]. Modular Machine Tool & Automatic Manufacturing Technique,2021(4):14-18.
[7] 庾天翼,李舜酩,龚思琪. 基于时频脊线和阶次分析的转子故障诊断[J]. 航空发动机,2022,48(1):40-46. YU Tianyi,LI Shunming,GONG Siqi. Rotor fault diagnosis based on time-frequency ridge and order analysis[J]. Aeroengine,2022,48(1):40-46.
[8] 郭瑜,秦树人,汤宝平,等. 基于瞬时频率估计的旋转机械阶比跟踪[J]. 机械工程学报,2003,39(3):32-36. DOI: 10.3901/JME.2003.03.032 GUO Yu,QIN Shuren,TANG Baoping,et al. Order tracking of rotating machinery based on instantaneous frequency estimation[J]. Chinese Journal of Mechanical Engineering,2003,39(3):32-36. DOI: 10.3901/JME.2003.03.032
[9] GUO Y,CHI Y L,HUANG Y Y,et al. Robust IFE based order analysis of rotating machinery in virtual instrument[J]. Journal of Physics:Conference Series,2006,48(1):647-652.
[10] 陈昊,张永祥,黄包裕. 基于阶次跟踪的变转速工况轴承故障诊断方法[J]. 轴承,2021(12):49-55. CHEN Hao,ZHANG Yongxiang,HUANG Baoyu. Fault diagnosis method for bearings under variable speed conditions based on order tracking method[J]. Bearing,2021(12):49-55.
[11] 曾陆洋,延九磊,刘峰,等. 一种针对无键相铁道车辆的旋转部件阶次跟踪方法[J]. 铁道机车车辆,2022,42(2):111-115. ZENG Luyang,YAN Jiulei,LIU Feng,et al. Order tracking method for rotating parts of non-keyphase railway vehicles[J]. Railway Locomotive & Car,2022,42(2):111-115.
[12] ZHAO Ming,LI Jing,WANG Xiufeng,et al. A tacho-less order tracking technique for large speed variations[J]. Mechanical Systems and Signal Processing,2013,40(1):76-90. DOI: 10.1016/j.ymssp.2013.03.024
[13] CHANG Yonggen,FAN Jiang,ZHU Zhencai,et al. Fault diagnosis of rotating machinery based on time-frequency decomposition and envelope spectrum analysis[J]. Journal of Vibroengineering,2017,19(2):943-954. DOI: 10.21595/jve.2017.17232
[14] ZHENG Zhi,JIANG Wanlu,WANG Zhenwei,et al. Gear fault diagnosis method based on local mean decomposition and generalized morphological fractal dimensions[J]. Mechanism & Machine Theory,2015,9:151-167.
[15] WANG Tianyang,LIANG Ming,LI Jianyong,et al. Rolling element bearing fault diagnosis via fault characteristic order (FCO) analysis[J]. Mechanical Systems & Signal Processing,2014,45(1):139-153.
[16] PAN M C,LIN Y F. Further exploration of Vold-Kalman-filtering order tracking with shaft-speed information-II:engineering applications[J]. Mechanical Systems and Signal Processing,2006,20(6):1410-1428. DOI: 10.1016/j.ymssp.2005.01.007
[17] 张杰,史治宇,赵宗爽. 基于线调频自适应分解的时变系统瞬时模态参数识别[J]. 振动与冲击,2020,39(22):103-109,118. ZHANG Jie,SHI Zhiyu,ZHAO Zongshuang. Instantaneous modal parameter identification of time-varying systems based on adaptive chirplet decomposition[J]. Journal of Vibration and Shock,2020,39(22):103-109,118.
[18] ZHAO Ming,LIN Jing,XU Xiaoqiang,et al. Tacholess envelope order analysis and its application to fault detection of rolling element bearings with varying speeds[J]. Sensors,2013,13(8):10856-10875. DOI: 10.3390/s130810856
[19] BORGHESANI P,RICCI R,CHATTERTON S,et al. A new procedure for using envelope analysis for rolling element bearing diagnostics in variable operating conditions[J]. Mechanical Systems and Signal Processing,2013,38(1):23-35. DOI: 10.1016/j.ymssp.2012.09.014
[20] WU Jie,ZI Yanyang,CHEN Jinglong,et al. A modified tacho-less order tracking method for the surveillance and diagnosis of machine under sharp speed variation[J]. Mechanism and Machine Theory,2018,128:508-527. DOI: 10.1016/j.mechmachtheory.2018.06.016
[21] 顾佶智,师蔚,胡定玉,等. 强背景噪声下基于谱峭度-波束形成轴承故障特征提取[J]. 噪声与振动控制,2022,42(3):110-115. GU Jizhi,SHI Wei,HU Dingyu,et al. Bearing fault feature extraction based on spectral kurtosis beamforming under strong noise background[J]. Noise and Vibration Control,2022,42(3):110-115.
-
期刊类型引用(8)
1. 张新磊，谢翠娟，许俊锋. 机器人自主探索规划方法和系统设计. 计算机与数字工程. 2024(10): 2908-2913+2959 . 
百度学术
2. 朱雷，闯喜宏，李磊，梁秋祥，魏铭毅. 输煤廊道巡检机器人智能避障控制方法设计. 自动化与仪器仪表. 2023(07): 210-213+218 . 百度学术
3. 郭爱军，刘建宇，郑安. 基于多传感器信息融合灭火机器人避障策略. 煤炭技术. 2022(04): 201-203 . 百度学术
4. 张燕. 基于模糊控制的智能移动机器人最优避障路线生成系统. 机械设计与制造工程. 2022(04): 86-90 . 百度学术
5. 杨春雨，张鑫. 煤矿机器人环境感知与路径规划关键技术. 煤炭学报. 2022(07): 2844-2872 . 百度学术
6. 岳仍瑞. 基于概率论的机器人避障方案规划. 信息记录材料. 2021(01): 178-179 . 百度学术
7. 刘曦，柳文轩，阿丽米热·阿布来提，麦吾兰·伊力哈木. 双目避障系统在桥式起重机上的应用. 现代制造技术与装备. 2021(10): 95-97 . 百度学术
8. 袁晓明，郝明锐. 煤矿无轨辅助运输无人驾驶关键技术与发展趋势研究. 智能矿山. 2020(01): 89-97 . 百度学术
其他类型引用(1)
下载:
计量
- 文章访问数: 304
- HTML全文浏览量: 81
- PDF下载量: 27
- 被引次数: 9
