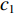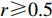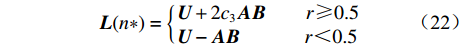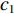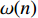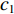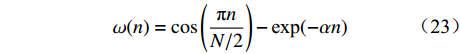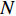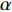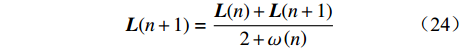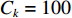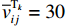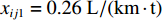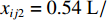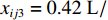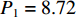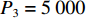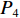Unmanned truck transportation scheduling in open-pit mines based on improved tunicate swarm algorithm
-
摘要: 针对露天矿无人驾驶卡车运输调度问题，以无人驾驶卡车燃油费用、固定启用费用、故障维修费用及网络基站建设与维护费用之和最小为目标函数，并以采矿场开采量、破碎场破碎量、卡车数量、卡车运输工作量为约束条件，建立了露天矿无人驾驶卡车运输调度优化模型。针对被囊群算法存在全局勘探和局部开采能力不平衡的问题，提出了一种基于Singer映射和参数位置自适应更新机制的改进被囊群算法（ITSA），并将其用于求解露天矿无人驾驶卡车运输调度优化模型。该算法引入Singer映射用于增强初始被囊种群在解空间中的分布性，加快压缩解空间大小，从而提高算法收敛速度；通过参数位置自适应更新机制调节被囊个体与最优被囊个体位置，以增大解空间的搜索范围，从而使算法跳出局部最优。仿真结果表明：与灰狼优化算法（GWO）、鲸鱼优化算法（WOA）、原子搜索优化算法（ASO）及被囊群算法（TSA）4种群智能优化算法相比，ITSA具有更好的收敛精度、收敛速度和稳定性能；在单峰基准函数上，ITSA的各项评价指标远优于其他4种算法，表明ITSA具有更好的局部开采能力；在多峰基准函数上，ITSA的各项评价指标表现出更好的寻优性能，表明ITSA具有更好的全局勘探性能。实际应用场景表明，ITSA用于求解无人驾驶卡车运输调度优化模型时具有更快的收敛速度和更高的收敛精度，且减少了卡车运输费用和运输距离。Abstract: In order to solve the problem of unmanned truck transportation scheduling in open-pit mines, the minimum sum of fuel cost, fixed start-up cost, breakdown maintenance cost, and network base station construction and maintenance cost are taken as the objective functions. The mining amount of mining station, crushing amount of crushing station, truck number and truck transportation workload are taken as the constraint conditions. The optimization model of unmanned truck transportation scheduling in open-pit mines is established. To solve the problem of imbalance between global exploration and local mining ability in the tunicate swarm algorithm, an improved tunicate swarm algorithm (ITSA) based on Singer mapping and adaptive updating mechanism of parameter position is proposed. And it is applied to solve the optimization model of unmanned truck transportation scheduling in open-pit mines. Singer mapping is introduced to enhance the distribution of the initial tunicate swarm in the solution space and accelerate the compression of the solution space, thus improving the convergence speed of the algorithm. Through the adaptive updating mechanism of parameter position, the positions of the tunicate and the optimal tunicate are adjusted to increase the search range of the solution space. Therefore, the algorithm jumps out of the local optimization. The simulation results show that ITSA has better convergence precision, convergence speed and stability compared with the four population intelligent optimization algorithms of grey wolf optimization algorithm (GWO), whale optimization algorithm (WOA), atom search optimization algorithm (ASO) and tunicate swarm algorithm (TSA). In the unimodal benchmark function, the evaluation indexes of ITSA are far better than those of the other four algorithms, which shows that ITSA has better local mining capacity. In the multi-peak benchmark function, the evaluation indexes of ITSA show better optimization performance, which indicates that ITSA has better global exploration performance. The practical application scenario verification shows that ITSA has faster convergence speed and higher convergence precision when used for solving the unmanned truck transportation scheduling optimization model. And ITSA reduces the truck transportation cost and transportation distance.
-
0. 引言
露天矿运输系统在露天矿生产过程中产生的运输费用占矿山运营成本的50%～60%[1-3]。无人驾驶卡车作为新一代人工智能与工程技术相结合的最新产物，近年来不断投入到各大露天矿中进行生产并取得了一定成果[4]。有研究表明，采用无人驾驶卡车代替传统有人驾驶卡车可大大降低露天矿运输成本。因此，研究露天矿无人驾驶卡车运输调度问题不仅可提高企业经济效益、降低能源消耗，而且对实现露天矿无人化和智能化开采具有重要意义[5-6]。与传统露天矿卡车运输调度相比，引入无人驾驶技术后，卡车对自身和环境的感知能力增强，能够为运输调度提供更多数据，使得调度优化模型可以考虑的目标函数和约束条件更为丰富；同时由于其无人化、少人化的管理方式，迫使无人驾驶卡车在运输调度过程中对网络通信有着更高的要求。但从本质上来看，无人驾驶卡车运输调度问题仍是研究运输成本最小化的问题。因此，原有针对有人驾驶卡车运输的调度优化算法仍可迁移至无人驾驶卡车运输调度优化模型的求解中。
近年来，群智能优化算法由于启发机制简单、对初始点不敏感等特点，被广泛应用于各种卡车调度问题。王金亮[7]以运输成本最小化为目标，建立了露天矿多车型卡车调度模型并利用遗传算法进行有效求解，同步实现了卡车利用率最大化和成本费用最小化。张明等[8]构建了露天矿的多目标卡车调度模型，并采用多目标遗传算法求解得到了Pareto最优解集，有效解决了露天矿卡车调度问题。张超等[9]为提高露天矿无人驾驶卡车效率，建立了露天矿无人驾驶卡车最优调度模型，并利用改进蚁群算法求解最优调度模型。王俊栋等[10]考虑装货点和卸货点间的运输成本，构建了露天矿运输调度优化数学模型，并以改进的量子粒子群算法为模型求解方案，一定程度上实现了露天矿卡车的合理运输调度。苏楷等[11]利用改进的果蝇优化算法求解露天矿运输调度优化模型，可有效降低露天矿运输成本，提高露天矿生产效率。此外，灰狼优化（Grey Wolf Optimization，GWO）算法[12]、差分进化算法[13]、鲸鱼优化算法（Whale Optimization Algorithm，WOA）[14]及原子搜索优化（Atom Search Optimization，ASO）算法[15]等群智能优化算法也被应用于求解露天矿卡车运输调度优化模型。上述算法在一定程度上解决了露天矿卡车运输调度问题，但存在收敛精度低和收敛速度慢的问题。
被囊群算法（Tunicate Swarm Algorithm，TSA）是S. Kaur等[16]于2020年提出的一种新型群智能优化算法。该算法在求解优化问题时所需参数少且寻优能力强，被广大学者应用于经济调度[17]、光伏参数优化[18]、电网优化设计[19]、资源分配[20]等工程优化问题中，但目前尚未发现有学者将其应用于求解露天矿无人驾驶卡车运输调度优化模型中。本文在TSA中引入Singer映射和参数位置自适应更新机制，提出了一种改进被囊群算法（Improved Tunicate Swarm Algorithm，ITSA），并将其应用于求解露天矿无人驾驶卡车运输调度优化模型。
1. 露天矿无人驾驶卡车运输调度优化模型
在露天矿实际开采过程中，多个采矿场和破碎站间协同工作，无人驾驶卡车将物料从采矿场运输至1个或多个破碎站进行破碎作业。采矿场到破碎站的运输距离不同，无人驾驶卡车产生的运输费用也不同。因此，本文将露天矿无人驾驶卡车运输调度问题看作是寻求卡车最小运输费用的问题。
在露天矿无人驾驶卡车运输过程中，无人驾驶卡车作业状态可简单分为空运、等装、装车、重运、等卸、卸车及故障7种。假设无人驾驶卡车从第i（i=1，2，…，I，I为采矿场数量）个采矿场
${{\text{M}}_i}$ 装车到第$j $ （j=1，2，…，J，J为破碎站数量）个破碎站${{\text{N}}_j}$ 卸车再回到采矿场${{\text{M}}_i}$ 等装为1次完整的运输调度过程，则该过程中产生的运输费用为燃油费用、固定启用费用、故障维修费用及网络基站建设与维护费用之和。(1) 燃油费用。在1次调度过程中产生的燃油费用z1为无人驾驶卡车空运、重运及卸车时所用燃油费用之和，即
$$ {{\textit{z}}_1} = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {[ {{P_1}({x_{ij1}} + {x_{ij2}}){d_{ij}}y_{ij}^{{{\rm{T}}_k}} + {P_1}{x_{ij3}}} ]} } } $$ (1) 式中：
${P_1}$ 为每辆无人驾驶卡车的单位燃油成本；${x_{ij1}}$ 为无人驾驶卡车空运状态下单位距离耗油量；${x_{ij2}}$ 为无人驾驶卡车重运状态下单位距离耗油量；${d_{ij}}$ 为无人驾驶卡车完成1次运输调度的距离，即无人驾驶卡车从采矿场${{\text{M}}_i}$ 装车到破碎站${{\text{N}}_j}$ 卸车再回到采矿场${{\text{M}}_i}$ 等装的距离；$y_{ij}^{{{\rm{T}}_k}}$ 为决策变量，$y_{ij}^{{{\rm{T}}_k}} = 1$ 表示第k（k=1，2，…，K，K为无人驾驶卡车数量）辆无人驾驶卡车Tk从采矿场${{\text{M}}_i}$ 到破碎站${{\text{N}}_j}$ 进行作业，$y_{ij}^{{{\rm{T}}_k}} = 0$ 表示第k辆无人驾驶卡车Tk未从采矿场${{\text{M}}_i}$ 到破碎站${{\text{N}}_j}$ 进行作业；${x_{ij3}}$ 为无人驾驶卡车卸车状态下耗油量。(2) 固定启用费用。由于无人驾驶卡车的固定启用费用与运输距离和装载量无关，所以在1次完整运输调度过程中产生的固定启用费用为
$$ {{\textit{z}}_2} = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {{P_2}y_{ij}^{{{\rm{T}}_k}}} } } $$ (2) 式中
${P_2}$ 为每辆无人驾驶卡车的固定启用费用。(3) 故障维修费用。在整个运输调度过程中，每辆无人驾驶卡车在任一状态下都可能发生故障，则故障维修费用为
$$ {{\textit{z}}_3} = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {{P_3}y_{ij}^{{{\rm{T}}_k}}} } } $$ (3) 式中
${P_3}$ 为每辆无人驾驶卡车的故障维修费用。(4) 网络基站建设与维护费用。由于无人驾驶卡车没有人员操控，卡车运输调度几乎全靠网络进行信息交互和共享，所以相对于有人驾驶卡车运输调度，无人驾驶卡车运输调度增加了网络基站建设与维护费用。网络基站建设费用为一次性的固定费用；网络维护费用与网络基站建设时间长短及环境天气有关。假设网络维护费用随着调度的进行呈非线性递增趋势，则在1次完整运输调度过程中产生的网络基站建设与维护费用为
$$ {{\textit{z}}_4} = {P_4} + \ln({t}/{\min}) $$ (4) 式中：
${P_4}$ 为网络基站建设费用；$t$ 为完整完成1次运输调度作业所用时间。由于无人驾驶卡车由电脑控制，其速度保持不变，所以可由无人驾驶卡车行驶的平均速度和路程计算
$t$ ，即$$ t = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {{P_5}\frac{{{d_{ij}}}}{{\overline v _{ij}^{{{\rm{T}}_k}}}}} } } $$ (5) 式中：
${P_5}$ 为网络维护费用；$\overline v _{ij}^{{{\rm{T}}_k}}$ 为第k辆无人驾驶卡车Tk完整完成1次运输调度作业的平均速度。将式（5）代入式（4），得
$$ {{\textit{z}}_4} = {P_4} + \ln \left[ {\sum\limits_{i = 1}^I} {\sum\limits_{j = 1}^J} {\sum\limits_{k = 1}^K} {(P_5/元)} \left( \frac{{d_{ij}}}{{\overline v _{ij}^ {{{\rm{T}}_k}} } } \Bigg/{\min}\right) \right]$$ (6) 无人驾驶卡车在1次完整运输调度过程中产生的运输费用
$Z = {z_1} + {z_2} + {z_3} + {z_4}$ 。因此，露天矿无人驾驶卡车运输调度优化模型为$$ \begin{split} \min \;Z =& \min ({{\textit{z}}_1} + {{\textit{z}}_2} + {{\textit{z}}_3} + {{\textit{z}}_4})= \hfill \\& \min \left\{ {\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {\left[ {{P_1}({x_{ij1}} + {x_{ij2}}){d_{ij}}y_{ij}^{{{\rm{T}}_k}} + {P_1}{x_{ij3}}} \right]} } } } \right.+ \hfill \\& \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {{P_2}y_{ij}^{{{\rm{T}}_k}}} } } + \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {{P_3}y_{ij}^{{{\rm{T}}_k}}} } } + \hfill \\& \left. { {P_4} + \ln \left[ {\sum\limits_{i = 1}^I} {\sum\limits_{j = 1}^J} {\sum\limits_{k = 1}^K} {(P_5/元)} \left(\frac{{{d_{ij}}}}{{\overline v_{ij}^ {{{\rm{T}}_k}} } }\Bigg/\min \right) \right]} \right\} \\[-20pt] \end{split} $$ (7) $$ {\text{s}}{\text{.}}\;{\text{t}}{\text{.}}\;\;\;\;\sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{C_k}y_{ij}^{{{\rm{T}}_k}}} } \leqslant \frac{{{Q_i}}}{S}\;\;\;\;\;\;\;\;\;\; $$ (8) $$ \sum\limits_{i = 1}^I {\sum\limits_{k = 1}^K {{C_k}y_{ij}^{{{\rm{T}}_k}}} } \leqslant \frac{{{g_j}}}{S} $$ (9) $$ \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {\sum\limits_{k = 1}^K {y_{ij}^{{{\rm{T}}_k}}} } } \leqslant K $$ (10) $$\;\; \sum\limits_{i = 1}^I {y_{ij}^{{{\rm{T}}_k}}} + \sum\limits_{j = 1}^J {y_{ij}^{{{\rm{T}}_k}}} = 0 $$ (11) $$ \sum\limits_{i = 1}^I {y_{ij}^{{{\rm{T}}_k}}} - \sum\limits_{j = 1}^J {y_{ji}^{{{\rm{T}}_k}}} = 0 $$ (12) $$ y_{ij}^{{{\rm{T}}_k}} = {{\{ 0,1 \} }} $$ (13) 式中：
${C_k}$ 为第k辆无人驾驶卡车Tk的装载量；${Q_i}$ 为采矿场${{\text{M}}_i}$ 的物料总开采量；S为1个目标生产计划中发生的无人驾驶卡车调度总次数；${g_j}$ 为破碎站${{\text{N}}_j}$ 的物料总破碎量；$y_{ji}^{{{\rm{T}}_k}}$ 为决策变量，$y_{ji}^{{{\rm{T}}_k}} = 1$ 表示第k辆无人驾驶卡车Tk从破碎站${{\text{N}}_j}$ 回到采矿场${{\text{M}}_i}$ 进行作业，$y_{ji}^{{{\rm{T}}_k}} = 0$ 表示第k辆无人驾驶卡车Tk未从破碎站${{\text{N}}_j}$ 回到采矿场${{\text{M}}_i}$ 进行作业。式(8)和式(9)表示无人驾驶卡车单次运输的物料量不超过采矿场1次开采量和破碎站1次破碎量；式(10)表示1次运输调度过程中使用的无人驾驶卡车不超过当次使用的卡车总数；式(11)和式(12)表示在整个运输调度过程中，每辆无人驾驶卡车不能从一个采矿场到另一个采矿场且每次完成破碎作业后必须回到原来的采矿场进行作业；式(13)表示无人驾驶卡车是否完整完成1次运输调度作业。
2. 基于Singer映射和参数位置自适应更新的ITSA
2.1 TSA
TSA是受被囊动物觅食行为启发，模拟被囊动物喷射推进和群体行为的一种群智能优化算法。为对被囊动物的喷射推进和群体行为进行数学建模，被囊动物应满足4个基本条件：避免被囊间冲突；向最佳被囊位置方向移动；向最佳被囊位置靠拢；群体行为。
(1) 避免被囊间冲突。计算新的被囊位置：
$$ {\boldsymbol{A}} = \frac{{\boldsymbol{G}}}{{\boldsymbol{M}}} $$ (14) $$ {\boldsymbol{G}} = {c_2} + {c_3} - {\boldsymbol{F}} $$ (15) $$ {\boldsymbol{F}} = 2{c_1} $$ (16) $$ {\boldsymbol{M}} = \left\lfloor {{{\boldsymbol{H}}_{\min }} + {c_1}\left( {{{\boldsymbol{H}}_{\max }} - {{\boldsymbol{H}}_{\min }}} \right)} \right\rfloor $$ (17) 式中：G为重力；M为被囊间的社会力量；
${c_1}$ —${c_3}$ 为[0，1]区间的随机数；F为深海水流平流；Hmin，Hmax分别为进行社交互动的初始速度和辅助速度。(2) 向最佳被囊位置方向移动。在避免被囊间冲突后，种群中的每个被囊都向最佳被囊位置方向移动。
$$ {\boldsymbol{B}} = \left| {{\boldsymbol{U}} - r{\boldsymbol{L}}(n)} \right| $$ (18) 式中：B为食物与被囊间的距离；U为食物的位置；
$r$ 为随机数；L(n)为被囊的位置；n为当前迭代次数。(3) 向最佳被囊位置靠拢。更新后的被囊位置为
$$ {\boldsymbol{L}}(n*) = \left\{ \begin{gathered} {\boldsymbol{U}} + {\boldsymbol{AB}}\qquad r \geqslant 0.5 \hfill \\ {\boldsymbol{U}} - {\boldsymbol{AB}}\qquad r < 0.5 \hfill \\ \end{gathered} \right. $$ (19) (4) 群体行为。为模拟被囊群群体行为的数学模型，TSA保存前2个最优解，然后根据最佳被囊位置更新其余被囊个体位置。该行为的数学模型定义为
$$ {\boldsymbol{L}}(n + 1) = \frac{{{\boldsymbol{L}}(n) + {\boldsymbol{L}}(n + 1)}}{{2 + {c_1}}} $$ (20) 2.2 ITSA
传统TSA存在全局勘探和局部开采能力不平衡的问题，本文从种群初始化、参数位置更新2个方面对TSA进行改进。
2.2.1 基于Singer映射的种群初始化
在群智能优化算法中，初始种群在解空间中的分布对算法求解最优值具有极大的约束作用[21]。初始种群在解空间中分布越均匀，算法搜索到最优值的概率越大。混沌映射策略因其遍历性、非重复性等特点被广泛用于群智能优化算法的初始种群生成中。因此，为增强被囊群在整个解空间的分布性，本文引入Singer映射代替TSA中的随机搜索策略对被囊群进行初始化。Singer映射的迭代公式为[22]
$$ \begin{split} {\varphi _{n + 1}} =& \mu \left( {7.86{\varphi _n} - 23.31\varphi _n^2} \right) +\hfill \\& \mu \left( {28.75\varphi _n^3 - 13.302\;875\varphi _n^4} \right) \end{split} $$ (21) 式中：
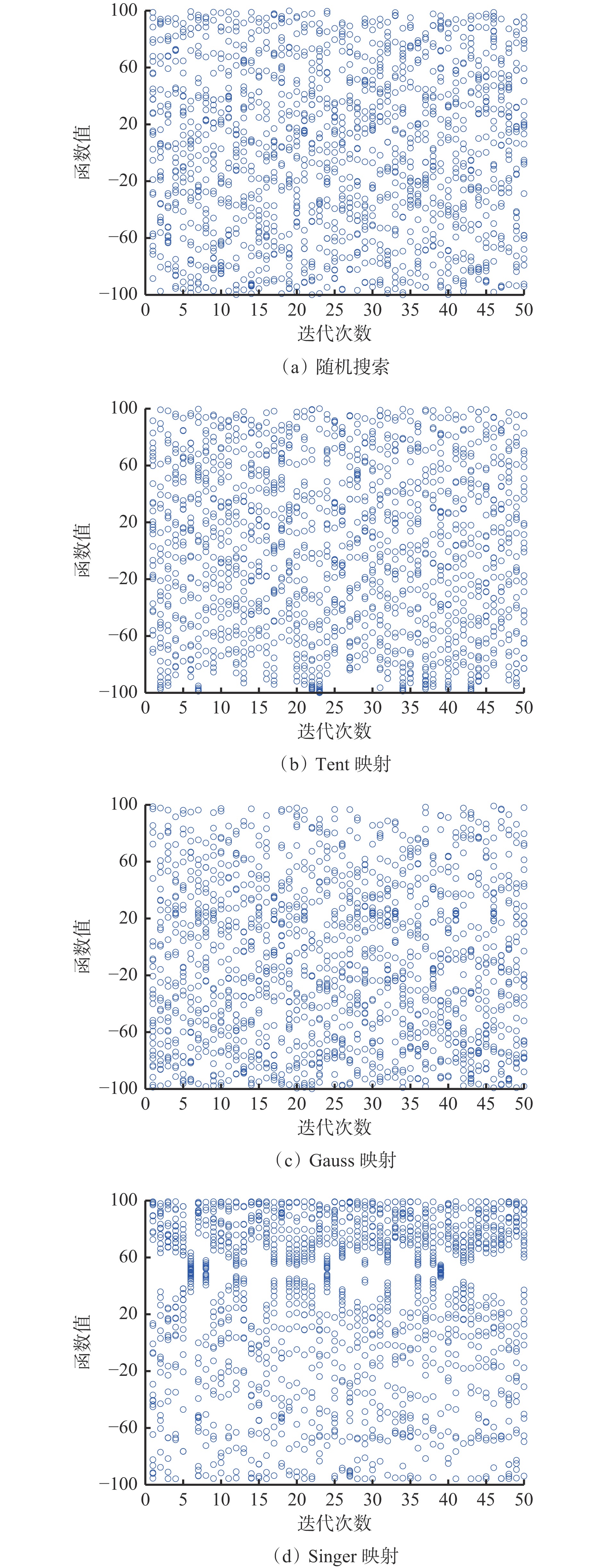
${\varphi _n}$ ，${\varphi _{n + 1}}$ 分别为第n次、第n+1次迭代值；$\;\mu $ 为常数，$\;\mu \in (0.9,1.08)$ 。为验证Singer映射生成的初始被囊群相对于随机搜索和其他常见混沌映射[22]具有更好的性能，本文对随机搜索、Tent映射、Gauss映射和Singer映射生成的初始被囊群位置进行对比，如图1所示。可看出，随机搜索、Tent映射和Gauss映射生成的初始被囊群在解空间中的分布更均匀，但Singer映射更有助于提高算法的收敛性能，加快算法在迭代初期的搜索速度。当初始被囊群在空间中的分布均匀时，在各个位置上的被囊搜索最优解均保持相同的迭代速度；而采用Singer映射生成的初始被囊群进行搜索时，由于在上边界分布的被囊个体更多，算法在初始迭代时很快便能对上边界进行遍历，能较快降低解空间大小，对后期算法求解最优值效果更佳。
![]()
图 1 不同方法生成的初始被囊群位置Figure 1. Initial tunicate swarm location generated by different methods2.2.2 参数位置自适应更新
在标准的TSA中，影响算法性能的重要因素是被囊群的位置更新方式，而被囊个体位置的更新由个体位置（当前和上一代个体位置）及[0，1]区间的随机参数
${c_1}$ 决定。为提高TSA性能，本文提出一种新的参数位置自适应更新策略来平衡TSA的全局勘探和局部开采能力。对于被囊个体位置，由式(19)可知，当生成的随机数
$r \geqslant 0.5$ 时，被囊个体远离当前最佳被囊个体去搜索全部解空间，其目的是使TSA跳出局部最优，从而增强算法的全局搜索能力。为增强算法搜索全局最优值的能力，本文增大当前被囊搜索步长以增强算法逃逸极值能力。式(19)可重新定义为$$ {\boldsymbol{L}}(n*) = \left\{ \begin{gathered} {\boldsymbol{U}} + 2{c_3}{\boldsymbol{AB}}\qquad r \geqslant 0.5 \hfill \\ {\boldsymbol{U}} - {\boldsymbol{AB}}\qquad \quad\; r ＜ 0.5 \hfill \\ \end{gathered} \right. $$ (22) 对于随机参数
${c_1}$ ，由式(20)可知，${c_1}$ 与个体位置呈反比关系：${c_1}$ 越大，个体位置更新步长越小，越有利于算法的局部开采能力；${c_1}$ 越小，个体位置更新步长越大，越有利于算法的全局勘探能力。但由于标准被囊群使用的${c_1}$ 是随机参数，使得算法在计算被囊位置时是随机波动的，没有很好地平衡算法的全局勘探和局部开采能力。针对上述问题，本文引入一种自适应权重因子
$\omega (n)$ 代替随机参数${c_1}$ 。$$ \omega (n) = \cos \left( {\frac{{\text{π}}n}{N/2}} \right) - {{\text{exp}}({ - \alpha n}}) $$ (23) 式中：
$N$ 为最大迭代次数；$\alpha $ 为控制自适应权值因子衰减和上升的参数，本文取0.25。因此，新的被囊群群体行为可重新定义为
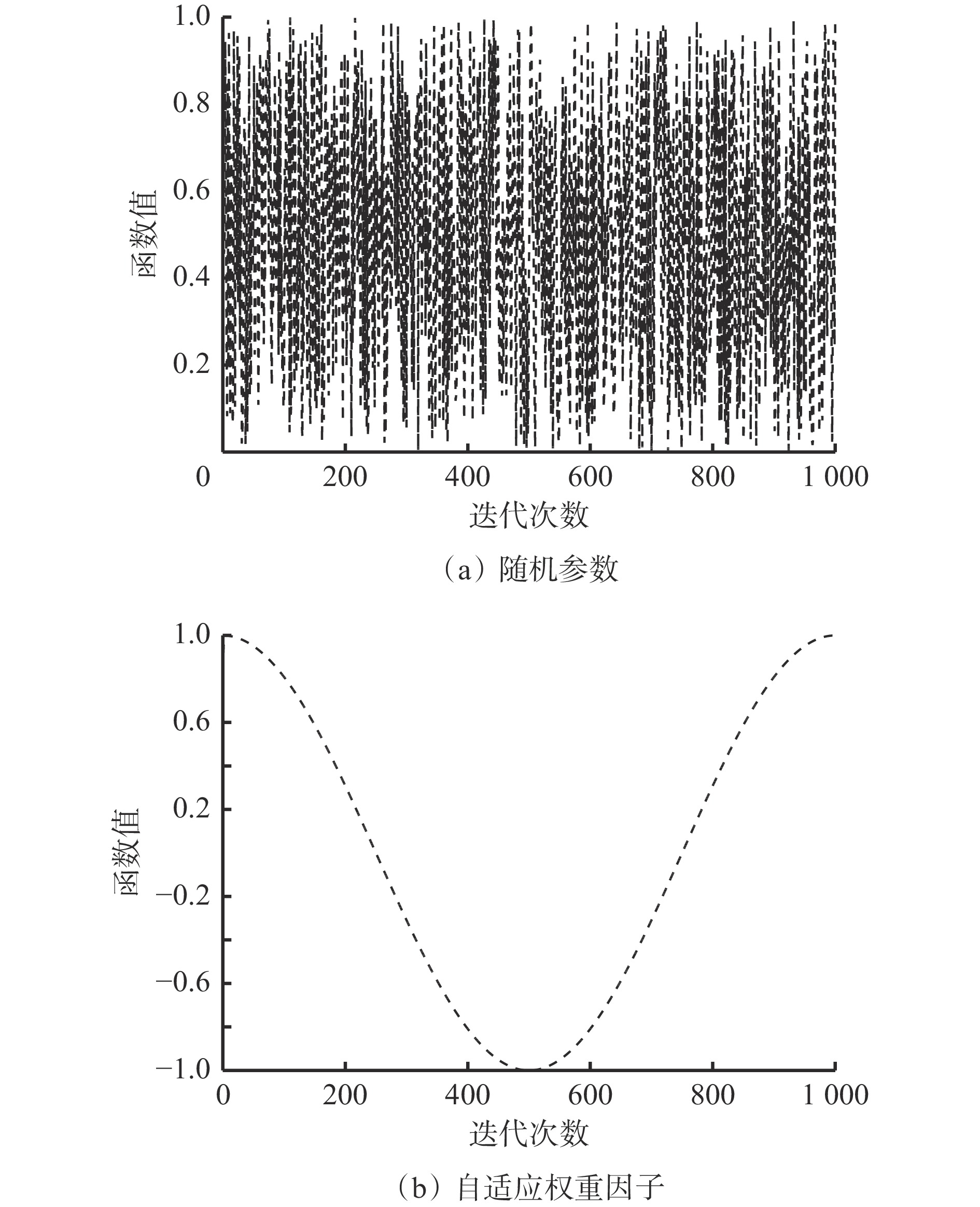
$$ {\boldsymbol{L}}(n + 1) = \frac{{{\boldsymbol{L}}(n) + {\boldsymbol{L}}(n + 1)}}{{2 + \omega \left( n \right)}} $$ (24) 为验证自适应权重因子相对于随机参数对算法具有更好的性能，分别利用随机参数和自适应权重因子生成函数值，如图2所示。可看出利用随机参数生成的函数值具有不确定性，对算法性能无显著影响；自适应权重因子对算法性能的影响可分为2个阶段，在自适应权重因子非线性递减阶段，TSA先勘探再开采，在自适应权重因子非线性递增阶段，TSA先开采再勘探。因此，采用自适应权重因子代替随机参数能更好地体现算法全局勘探和局部开采能力。
![]()
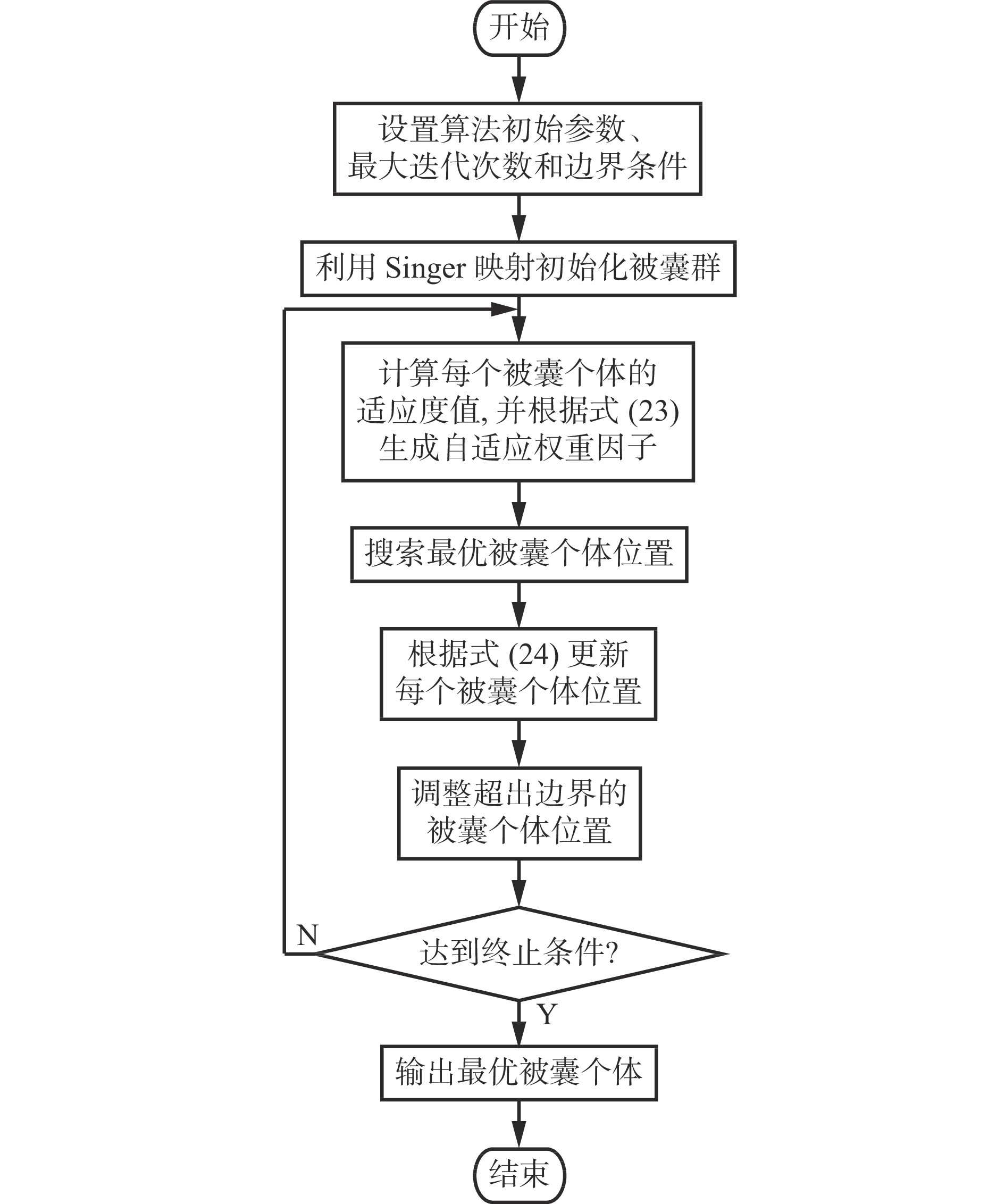
图 2 基于随机参数和自适应权重因子生成的函数值Figure 2. Function values generated by random parameters and adaptive weighting factors2.3 ITSA流程
ITSA流程如图3所示。
3. 仿真实验及结果分析
3.1 ITSA性能分析
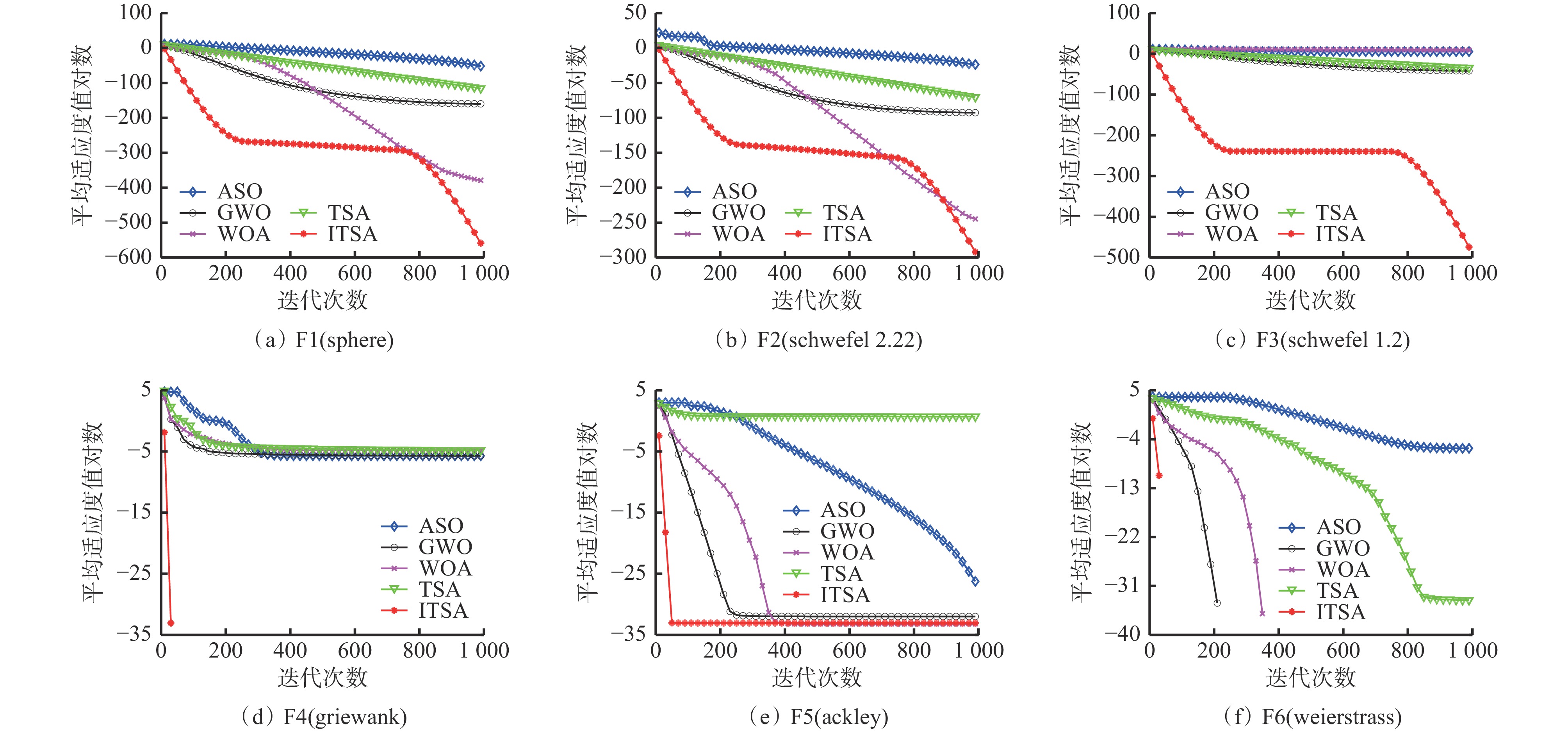
为验证ITSA具有更好的寻优和收敛性能，与GWO，WOA，ASO，TSA进行对比分析，不同群智能优化算法在6个基准函数（3个单峰基准函数和3个多峰基准函数）下进行30次独立重复实验，得到的基准函数寻优结果见表1，寻优收敛曲线如图4所示。
表 1 不同群智能优化算法的基准函数寻优结果Table 1. Benchmark function optimization results of different swarm intelligence optimization algorithms函数 评价指标 GWO WOA ASO TSA ITSA F1(sphere) 平均值 3.62×10−70 4.20×10−166 2.02×10−23 1.72×10−51 3.64×10−250 标准差 1.04×10−69 0 1.57×10−23 8.53×10−51 0 F2(schwefel 2.22) 平均值 6.08×10−41 1.81×10−107 4.89×10−11 1.29×10−31 6.04×10−131 标准差 7.22×10−41 9.56×10−107 4.71×10−11 1.16×10−31 2.43×10−130 F3(schwefel 1.2) 平均值 5.90×10−19 9.93×103 2.21×102 7.66×10−16 6.28×10−213 标准差 2.17×10−18 5.85×103 1.33×102 3.58×10−15 0 F4(griewank) 平均值 3.36×10−3 8.10×10−3 3.36×10−3 8.24×10−3 0 标准差 7.20×10−3 2.62×10−2 7.15×10−3 1.36×10−2 0 F5(ackley) 平均值 1.28×10−14 3.85×10−15 3.28×10−12 2.04 4.44×10−15 标准差 2.72×10−15 2.30×10−15 1.83×10−12 1.48 0 F6(weierstrass) 平均值 0 0 3.26×10−3 2.13×10−15 0 标准差 0 0 1.30×10−2 4.63×10−15 0 ![]()
图 4 不同群智能优化算法对基准函数的寻优收敛曲线Figure 4. Optimal convergence curves of different swarm intelligence optimization algorithms for benchmark functions由表1和图4可知，从整体来看，ITSA相对于其他4种群智能优化算法具有更好的收敛精度、收敛速度和稳定性能。在单峰基准函数（F1，F2，F3）上，ITSA的各项评价指标远优于其他4种算法，表明ITSA具有更好的局部开采能力。在多峰基准函数（F4，F5，F6）上，ITSA的各项评价指标除在F5上的平均值上略低于WOA外，在其他基准函数上都表现出更好的寻优性能，表明ITSA具有更好的全局勘探能力。
可见，ITSA相较于其他4种算法很好地平衡了算法寻优过程中的全局勘探和局部开采能力。另外通过6个基准函数的寻优结果及收敛曲线证明了ITSA具有更好的可靠性和鲁棒性。
3.2 露天矿运输调度实例分析
为验证本文建立的无人驾驶卡车运输调度优化模型及ITSA在实际应用场景中求解模型的有效性，以胜利露天煤矿实际无人驾驶卡车运输调度数据为例，将ITSA应用于求解露天矿无人驾驶卡车运输调度优化模型，并与GWO，WOA，ASO，TSA 4种群智能优化算法进行对比分析。
本文研究的无人驾驶卡车仅在露天矿中某一封闭区域内进行生产，在该区域内包含8个采矿场和1个破碎站，每个采矿场到破碎站均有3条路线，不同路线距离见表2。每辆无人驾驶卡车的装载量
${C_k} = 100$ t；平均车速$\overline v_{ij}^{{{\rm{T}}_k}} = 30$ km/h；无人驾驶卡车在空运状态下单位距离耗油量${x_{ij1}} = 0.26{\text{ L}}/({\rm{km}}\cdot{\text{t}} )$ ，重运状态下单位距离耗油量${x_{ij2}} = 0.54{\text{ L}} / {({\text{km}}\cdot {\text{t}})}$ ，卸车状态下耗油量${x_{ij3}} =0.42{\text{ L}} / {({\text{km}}\cdot {\text{t}})}$ ；每辆无人驾驶卡车单位燃油成本${P_1} = 8.72$ 元/L，固定启用费用P2 = 24元，故障维修费用${P_3} = 5\;000$ 元；网络基站建设费用${P_4}$ 为定值，在求解运输调度优化模型时不予考虑。表 2 采矿场至破碎站不同路线距离Table 2. Route distance between mining station and crushing stationkm 采矿场 采矿场至破碎站距离 路线1 路线2 路线3 M1 3.593 3.612 3.485 M2 2.217 2.322 2.107 M3 1.676 1.602 1.701 M4 3.457 3.552 3.388 M5 3.437 3.306 3.521 M6 3.325 3.232 3.476 M7 3.072 2.998 3.102 M8 3.585 3.655 3.475 文中所有求解算法的初始种群个数均设置为100，算法迭代次数均设置为200次。以露天矿无人驾驶卡车运输调度优化模型的目标函数（式（7））作为适应度函数，利用Matlab2020b对模型进行仿真求解，在调用相同数量的无人驾驶卡车进行1次完整运输调度作业后，得到GWO，WOA，ASO，TSA，ITSA的模型求解结果（表3）和迭代收敛曲线（图5）。
表 3 不同群智能优化算法下模型求解结果Table 3. Model solution results under different swarm intelligence optimization algorithms算法 最小运输费用/元 卡车运输距离/km GWO 8 360.317 42.356 WOA 8 586.490 45.751 ASO 8 806.126 46.861 TSA 8 535.574 43.362 ITSA 8 248.042 41.936 ![]()
图 5 不同群智能优化算法的迭代收敛曲线Figure 5. Iterative convergence curves of different swarm intelligence optimization algorithms由表3可知，利用ITSA求解得到的模型结果最佳；与ASO求解结果相比，利用ITSA求解得到的最小运输费用减少了558.084元，卡车运输距离减少了4.925 km。
从图5可看出，ITSA在求解模型时具有更快的收敛速度和收敛精度。这是由于ITSA在迭代过程中采用Singer映射增强了生成的初始种群对解空间的探索能力，加快了迭代初期被囊动物靠近食物的速度；同时采用自适应参数代替随机参数对被囊动物位置进行自适应扰动，不仅促使被囊动物更快接近食物，还提高了被囊动物向四周搜索食物的可能。
4. 结论
(1) 针对露天矿无人驾驶卡车运输调度问题，从卡车燃油费用、固定启用费用、故障维修费用及网络基站建设与维护费用4个方面，构建了露天矿无人驾驶卡车运输调度优化模型。
(2) 针对TSA全局勘探与局部开采能力不平衡的问题，引入Singer映射和参数位置自适应更新机制平衡TSA的局部开采和全局勘探能力，提出了ITSA。通过仿真验证了ITSA相较于其他群智能优化算法（GWO，WOA，ASO，TSA）具有更高的寻优性能和鲁棒性。
(3) 将ITSA用于求解露天矿无人驾驶卡车运输调度优化模型，不仅提高了算法收敛精度和收敛速度，而且减少了卡车运输费用和运输距离。
-
![]()
图 1 不同方法生成的初始被囊群位置
Figure 1. Initial tunicate swarm location generated by different methods
![]()
图 2 基于随机参数和自适应权重因子生成的函数值
Figure 2. Function values generated by random parameters and adaptive weighting factors
![]()
图 4 不同群智能优化算法对基准函数的寻优收敛曲线
Figure 4. Optimal convergence curves of different swarm intelligence optimization algorithms for benchmark functions
![]()
图 5 不同群智能优化算法的迭代收敛曲线
Figure 5. Iterative convergence curves of different swarm intelligence optimization algorithms
表 1 不同群智能优化算法的基准函数寻优结果
Table 1 Benchmark function optimization results of different swarm intelligence optimization algorithms
函数 评价指标 GWO WOA ASO TSA ITSA F1(sphere) 平均值 3.62×10−70 4.20×10−166 2.02×10−23 1.72×10−51 3.64×10−250 标准差 1.04×10−69 0 1.57×10−23 8.53×10−51 0 F2(schwefel 2.22) 平均值 6.08×10−41 1.81×10−107 4.89×10−11 1.29×10−31 6.04×10−131 标准差 7.22×10−41 9.56×10−107 4.71×10−11 1.16×10−31 2.43×10−130 F3(schwefel 1.2) 平均值 5.90×10−19 9.93×103 2.21×102 7.66×10−16 6.28×10−213 标准差 2.17×10−18 5.85×103 1.33×102 3.58×10−15 0 F4(griewank) 平均值 3.36×10−3 8.10×10−3 3.36×10−3 8.24×10−3 0 标准差 7.20×10−3 2.62×10−2 7.15×10−3 1.36×10−2 0 F5(ackley) 平均值 1.28×10−14 3.85×10−15 3.28×10−12 2.04 4.44×10−15 标准差 2.72×10−15 2.30×10−15 1.83×10−12 1.48 0 F6(weierstrass) 平均值 0 0 3.26×10−3 2.13×10−15 0 标准差 0 0 1.30×10−2 4.63×10−15 0 
下载: 导出CSV
表 2 采矿场至破碎站不同路线距离
Table 2 Route distance between mining station and crushing station
km 采矿场 采矿场至破碎站距离 路线1 路线2 路线3 M1 3.593 3.612 3.485 M2 2.217 2.322 2.107 M3 1.676 1.602 1.701 M4 3.457 3.552 3.388 M5 3.437 3.306 3.521 M6 3.325 3.232 3.476 M7 3.072 2.998 3.102 M8 3.585 3.655 3.475
下载: 导出CSV
表 3 不同群智能优化算法下模型求解结果
Table 3 Model solution results under different swarm intelligence optimization algorithms
算法 最小运输费用/元 卡车运输距离/km GWO 8 360.317 42.356 WOA 8 586.490 45.751 ASO 8 806.126 46.861 TSA 8 535.574 43.362 ITSA 8 248.042 41.936
下载: 导出CSV
-
[1] 付恩三,刘光伟,邸帅,等. 露天矿山无人驾驶技术及系统架构研究[J]. 煤炭工程,2022,54(1):34-39. FU Ensan,LIU Guangwei,DI Shuai,et al. Unmanned driving technology and system architecture in open-pit mines[J]. Coal Engineering,2022,54(1):34-39.
[2] 常永刚. 露天矿运输系统优化与卡车调度问题研究[D]. 沈阳: 沈阳工业大学, 2018. CHANG Yonggang. Study on optimization of transportation system and truck scheduling in the open-pit[D]. Shenyang: Shenyang University of Technology, 2018.
[3] 王富民,贺昌斌. 露天矿卡车无人驾驶技术的现状与展望[J]. 露天采矿技术,2021,36(3):45-47. WANG Fumin,HE Changbin. Status and outlook of autonomous driving technology for trucks in open-pit mine[J]. Opencast Mining Technology,2021,36(3):45-47.
[4] 马琳. 露天矿卡车调度优化研究[D]. 天津: 河北工业大学, 2015. MA Lin. Optimization of truck dispating in open pit mine[D]. Tianjin: Hebei University of Technology, 2015.
[5] 莫明慧. 露天矿无人驾驶卡车多目标车流分配调度算法及应用[D]. 西安: 西安建筑科技大学, 2020. MO Minghui. Application of multi-objective traffic assignment and scheduling algorithm for driverless truck in open pit mine[D]. Xi'an: Xi'an University of Architecture and Technology, 2020.
[6] 武讲,郑群飞. 哈尔乌素露天矿无人驾驶方案研究[J]. 金属矿山,2021,50(2):167-172. WU Jiang,ZHENG Qunfei. Feasibility study of driverless system in Harwusu Open-pit Coal Mine[J]. Metal Mine,2021,50(2):167-172.
[7] 王金亮. 基于遗传算法的多车型露天矿卡车调度模型研究[J]. 现代矿业,2021,37(3):35-39,44. DOI: 10.3969/j.issn.1674-6082.2021.03.009 WANG Jinliang. Model research of multi-type truck scheduling based on GA[J]. Modern Mining,2021,37(3):35-39,44. DOI: 10.3969/j.issn.1674-6082.2021.03.009
[8] 张明,顾清华,李发本,等. 基于多目标遗传算法的露天矿卡车调度优化研究[J]. 金属矿山,2019,48(6):157-162. ZHANG Ming,GU Qinghua,LI Faben,et al. Research of open-pit mine truck dispatching optimization based on multi-objective genetic algorithm[J]. Metal Mine,2019,48(6):157-162.
[9] 张超,江松. 基于改进蚁群算法的露天矿无人驾驶卡车智能调度[J]. 安徽工业大学学报(自然科学版),2020,37(3):267-275. DOI: 10.3969/j.issn.1671-7872.2020.03.012 ZHANG Chao,JIANG Song. Intelligent dispatching of unmanned truck in open pit mine based on improved ant colony algorithm[J]. Journal of Anhui University of Technology(Natural Science),2020,37(3):267-275. DOI: 10.3969/j.issn.1671-7872.2020.03.012
[10] 王俊栋,李宁,吴亚辉,等. 基于改进DCW−QPSO算法的露天矿卡车调度优化方法[J]. 金属矿山,2019,48(12):156-162. WANG Jundong,LI Ning,WU Yahui,et al. Truck scheduling optimization in open pit mines based on improved DCW-QPSO algorithm[J]. Metal Mine,2019,48(12):156-162.
[11] 苏楷,门飞. 露天矿运输调度问题求解的自适应果蝇优化算法[J]. 金属矿山,2017,46(11):172-176. DOI: 10.3969/j.issn.1001-1250.2017.11.034 SU Kai,MEN Fei. Adaptive fruit fly optimization algorithm for solving open-pit hauling dispatching optimization problem[J]. Metal Mine,2017,46(11):172-176. DOI: 10.3969/j.issn.1001-1250.2017.11.034
[12] 门飞,蒋欣. 求解露天矿低碳运输调度问题的改进灰狼优化算法[J]. 工矿自动化,2020,46(12):90-94. MEN Fei,JIANG Xin. Improved gray wolf optimization algorithm for solving low-carbon transportation scheduling problem in open-pit mines[J]. Industry and Mine Automation,2020,46(12):90-94.
[13] 彭程,隋晓梅,王辉俊. 用于求解露天矿运输问题的改进差分进化算法[J]. 工矿自动化,2018,44(4):104-108. PENG Cheng,SUI Xiaomei,WANG Huijun. Improved differential evolution algorithm for solving open-pit mine transportation problem[J]. Industry and Mine Automation,2018,44(4):104-108.
[14] DEWI S K,UTAMA D M. A new hybrid whale optimization algorithm for green vehicle routing problem[J]. Systems Science & Control Engineering,2021,9(1):61-72.
[15] ZHAO Weiguo,WANG Liying,ZHANG Zhenxing. Atom search optimization and its application to solve a hydrogeologic parameter estimation problem[J]. Knowledge-Based Systems,2019,163:283-304. DOI: 10.1016/j.knosys.2018.08.030
[16] KAUR S,AWASTHI L K,SANGAL A L,et al. Tunicate swarm algorithm:a new bio-inspired based metaheuristic paradigm for global optimization[J]. Engineering Applications of Artificial Intelligence,2020,90:103541. DOI: 10.1016/j.engappai.2020.103541
[17] LI Lingling,LIU Zhifeng,TSENG M L,et al. Improved tunicate swarm algorithm:solving the dynamic economic emission dispatch problems[J]. Applied Soft Computing,2021,108:107504. DOI: 10.1016/j.asoc.2021.107504
[18] SHARMA A,DASGOTRA A,TIWARI S K,et al. Parameter extraction of photovoltaic module using tunicate swarm algorithm[J]. Electronics,2021,10(8):878. DOI: 10.3390/electronics10080878
[19] FETOUH T,ELSAYED A M. Optimal control and operation of fully automated distribution networks using improved tunicate swarm intelligent algorithm[J]. IEEE Access,2020,8:129689-129708. DOI: 10.1109/ACCESS.2020.3009113
[20] YADAV K,ALSHUDUKHI J S,DHIMAN G,et al. iTSA:an improved tunicate swarm algorithm for defensive resource assignment problem[J]. Soft Computing,2022,26(10):4929-4937. DOI: 10.1007/s00500-022-06979-z
[21] 刘威, 郭直清, 姜丰, 等. 协同围攻策略改进的灰狼算法及其PID参数优化[J/OL]. 计算机科学与探索: 1-16 [2022-04-09]. http://202.199.233.17:8000/rwt/CNKI/http/NNYHGLUDN3WXTLUPMW4A/kcms/detail/11.5602.tp.20210714.1741.002.html. LIU Wei, GUO Zhiqing, JIANG Feng, et al. Improved grey wolf optimizer based on cooperative attack strategy and its PID parameter optimization[J/OL]. Journal of Frontiers of Computer Science and Technology: 1-16[2022-04-09]. http://202.199.233.17:8000/rwt/CNKI/http/NNYHGLUDN3WXTLUPMW4A/kcms/detail/11.5602.tp.20210714.1741.002.html.
[22] KHISHE M,MOSAVI M R. Chimp optimization algorithm[J]. Expert Systems with Applications,2020,149:113338. DOI: 10.1016/j.eswa.2020.113338
-
期刊类型引用(5)
1. 薛棋文，丁震. 基于5G通信的露天矿矿用卡车采掘运输自动化控制方法. 矿业研究与开发. 2024(08): 206-213 . 
百度学术
2. 邢轩瑞，徐状状. 基于蚁群算法的铝土矿运输网络智能调度. 世界有色金属. 2024(21): 19-21 . 百度学术
3. 李新华. 基于多智能体强化学习的露天矿车辆调度方法. 西安邮电大学学报. 2023(01): 104-110 . 百度学术
4. 柴岩，李广友，任生，许兆楠. 多策略融合改进的自适应被囊群算法. 计算机应用研究. 2023(09): 2694-2703+2712 . 百度学术
5. 王晓玲，韩国玺，余佳，王佳俊，徐国鑫，肖尧. TBM掘进速率区间预测Bootstrap-IHHO-BiLSTM模型. 水力发电学报. 2023(12): 159-171 . 百度学术
其他类型引用(13)
计量
- 文章访问数: 1102
- HTML全文浏览量: 173
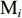
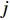
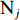
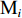
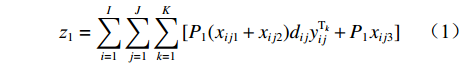
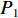
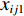
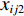
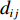
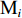
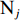
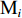
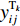
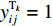
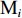
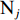
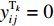
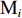
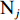
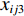
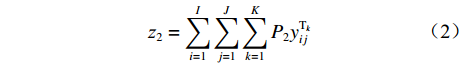
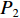
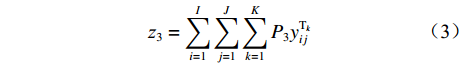
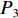
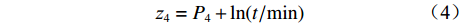
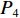
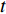
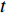
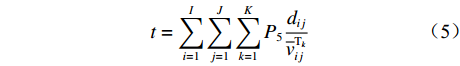
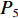
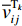
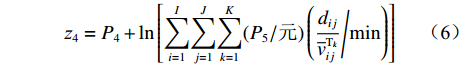
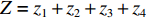
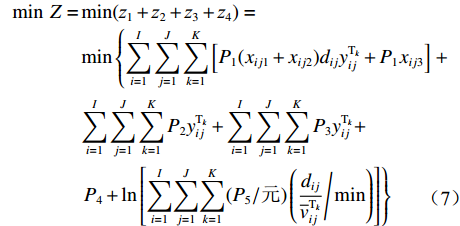
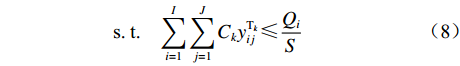
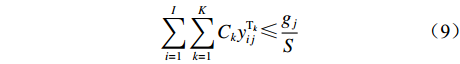
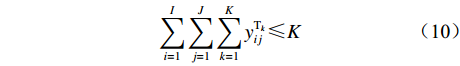
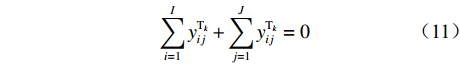
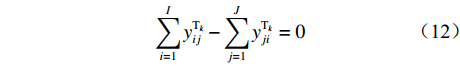
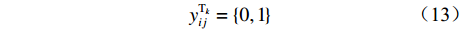
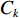
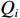
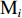
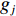
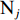
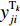
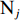
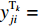
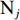
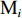
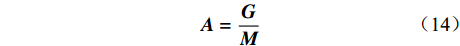
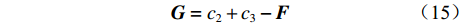
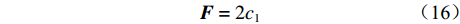
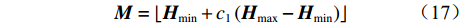
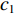
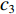
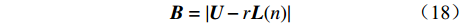
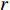
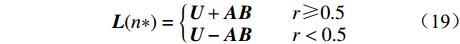
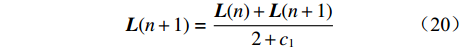
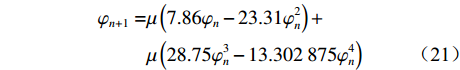
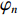
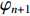
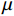
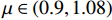
- PDF下载量: 65
- 被引次数: 18
