Fault line selection method for coal mine power grid based on RCMDE and KFCM
-
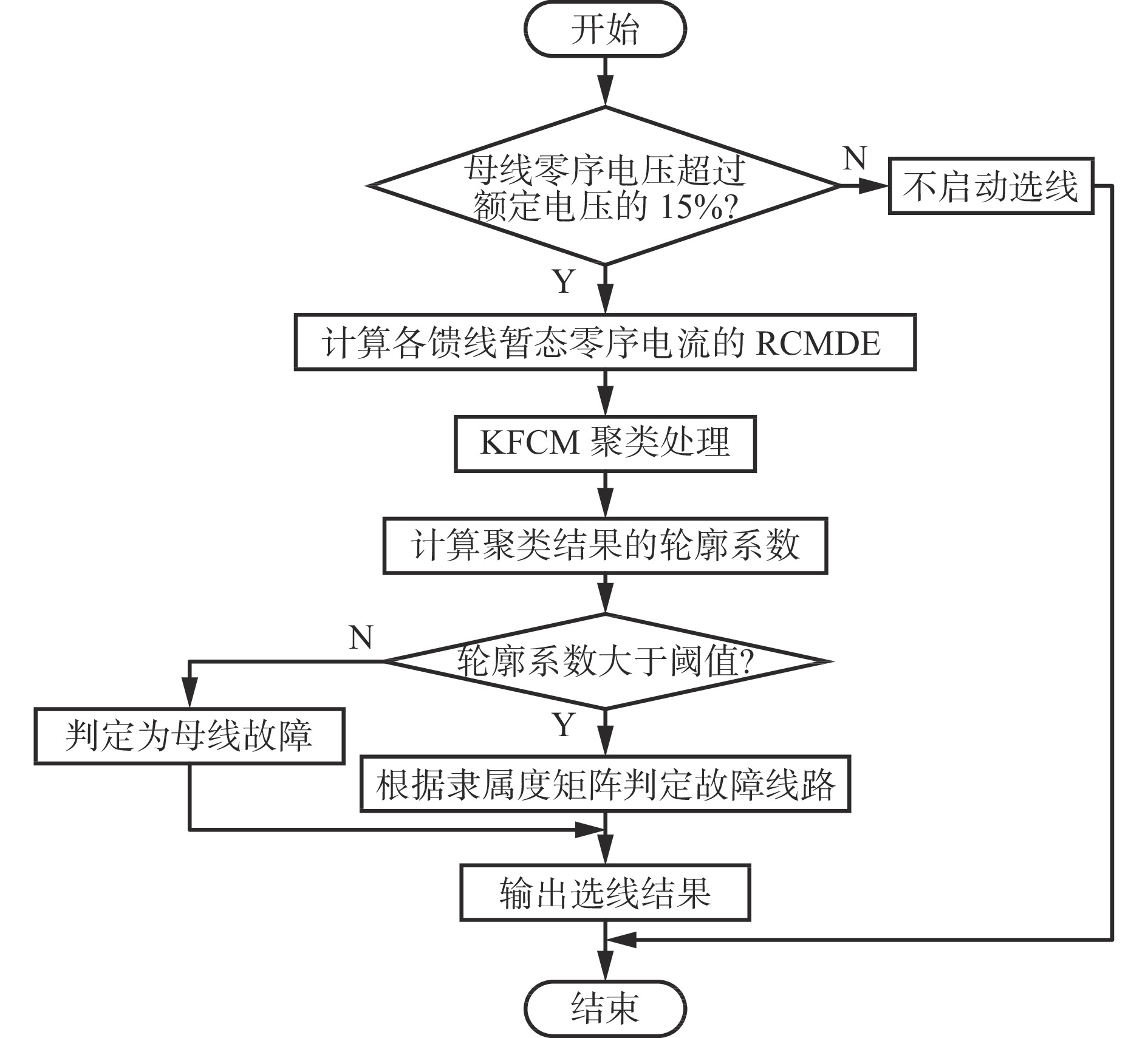
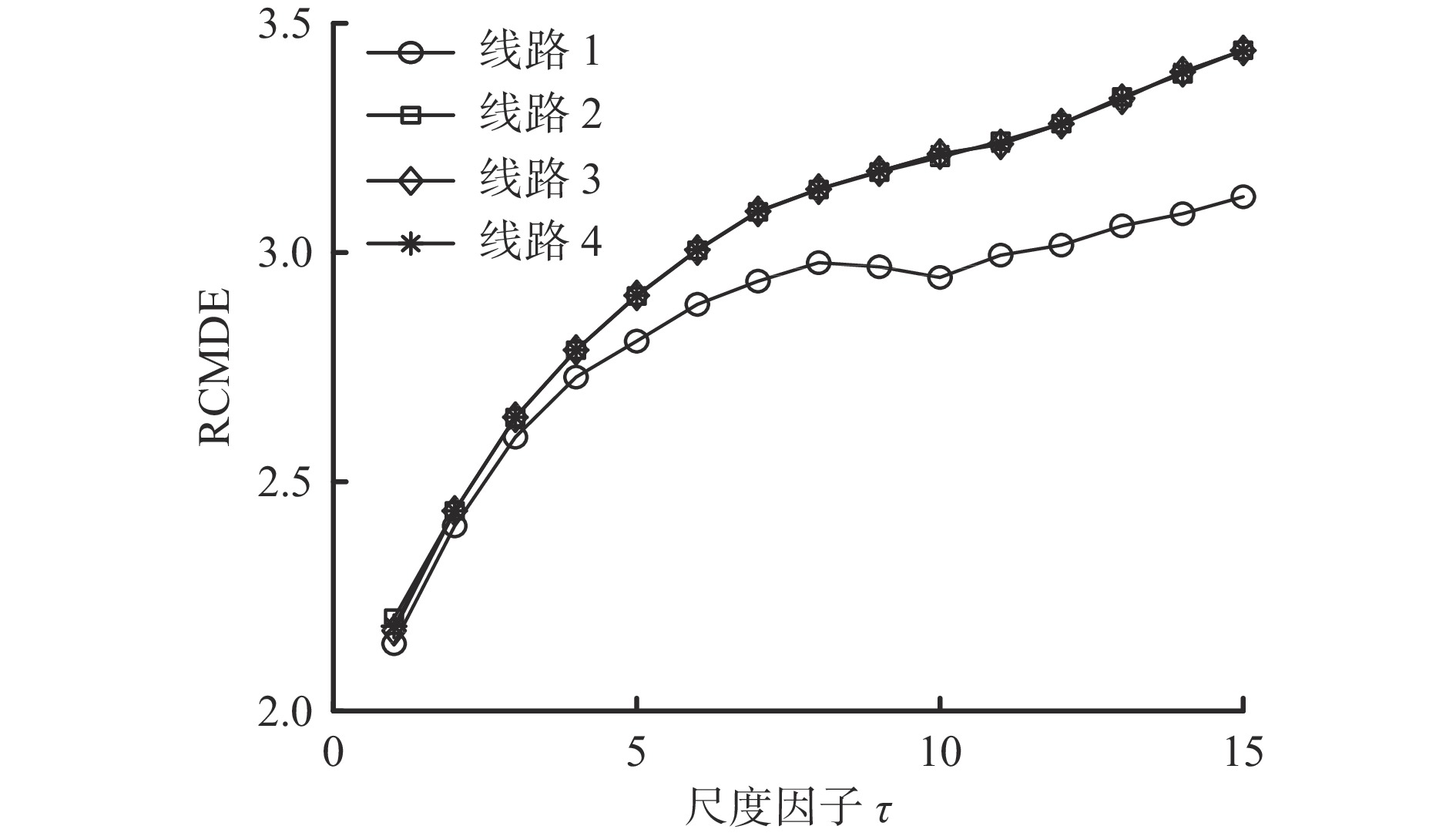
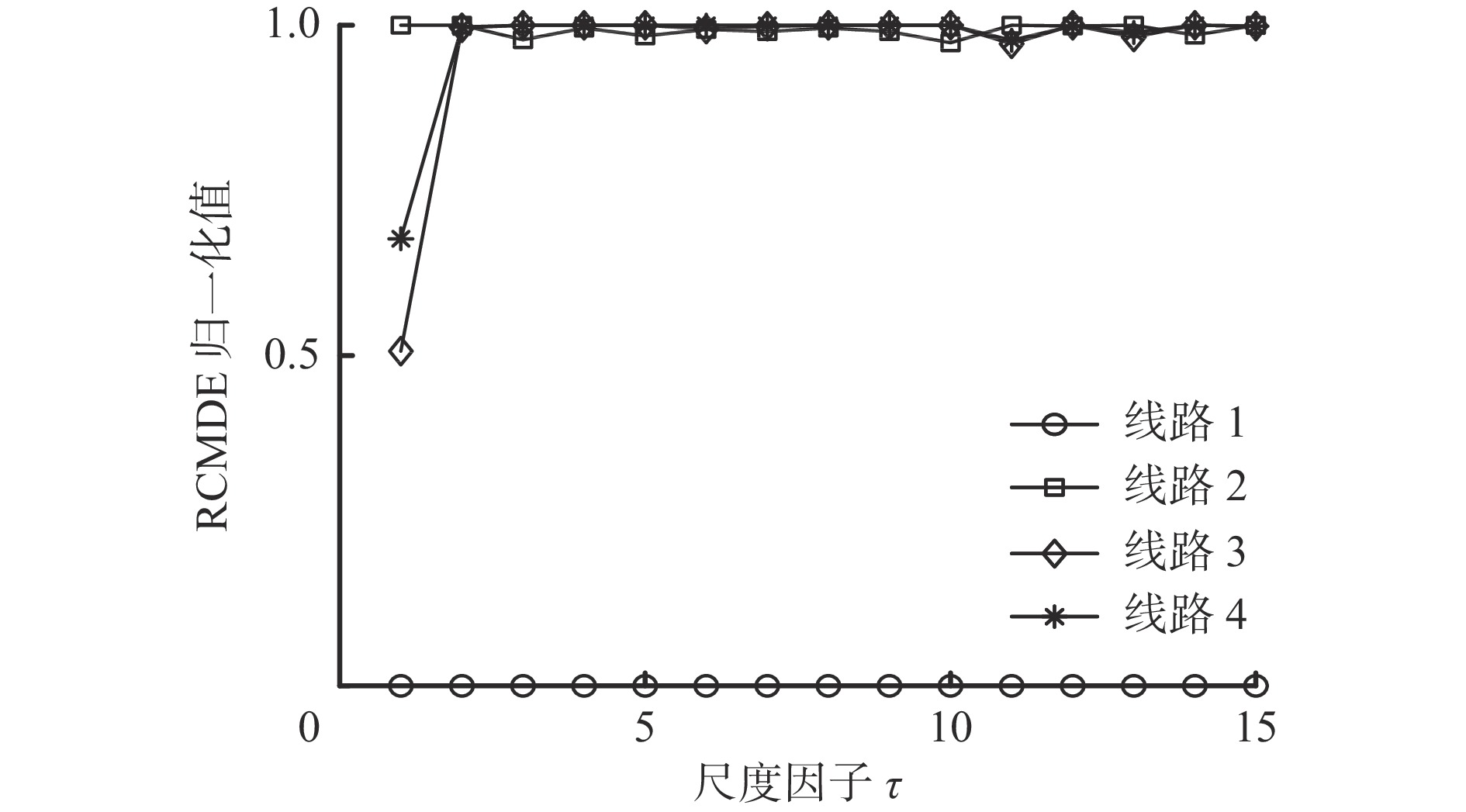
摘要: 针对普遍采用谐振接地系统的煤矿电网发生单相接地故障时难以准确选线的问题，提出一种基于精细复合多尺度散布熵( RCMDE)和核模糊C均值聚类( KFCM)的煤矿电网故障选线方法。以幅值、极性和波形相似度作为选线特征量具有以下局限性：基于幅值和极性差异的选线方法适用性有限；若线路中的零序电流互感器极性接反，基于极性的方法直接失效；采样不同步时，基于波形相似度的选线方法难以得到正确结果。为克服上述局限性，引入RCMDE来度量各线路暂态零序电流信号的复杂程度和不规则度，以RCMDE作为选线特征量。采用KFCM算法对RCMDE进行聚类分析，以实现故障线路自动识别，并通过判断轮廓系数是否超过阈值来区分母线故障和馈线故障。最后，通过聚类得到的隶属度矩阵判断馈线故障点所在线路。仿真结果表明：① 故障点所在的故障线路对应的RCMDE曲线与非故障线路间具有较大差异，可分为2类。RCMDE可作为筛选故障线路的特征指标。② 发生母线故障时聚类结果中存在平均轮廓系数小于阈值的分簇，而发生馈线故障时聚类结果各分簇的轮廓系数均大于阈值，在各类故障场景下，基于RCMDE和KFCM的煤矿电网故障选线方法均能实现正确选线，说明其准确性不受故障线路、故障位置、故障合闸角及接地电阻等因素的影响。③ 在噪声干扰情况下，基于RCMDE和KFCM的煤矿电网故障选线方法在小电阻接地或高阻接地情况下均能实现正确选线，具有较强的抗干扰能力。④ 在采样不同步及故障线路零序电流互感器极性反接等情况下，基于RCMDE和KFCM的煤矿电网故障选线方法仍可实现正确选线，选线结果具有较高的鲁棒性。Abstract: It is difficult to accurately select the fault line when the single-phase ground fault occurs in the coal mine power grid with the widely used resonant grounding system. In order to solve the above problem, a fault line selection method of the coal mine power grid based on the refined composite multiscale dispersion entropy (RCMDE) and the kernel fuzzy C-means clustering (KFCM) is proposed. The limitations of using amplitude, polarity and waveform similarity as line selection characteristic quantities: the applicability of the line selection method based on amplitude and polarity difference is limited. If the polarity of the zero sequence current transformer in the line is reversed, the method based on polarity will directly fail. When the sampling is not synchronized, the line selection method based on waveform similarity is difficult to obtain correct results. In order to overcome the above limitations, RCMDE is introduced to measure the complexity and irregularity of the transient zero sequence current signal of each line. RCMDE is used as the characteristic quantity of line selection. The KFCM algorithm is used to cluster the RCMDE to realize the automatic identification of fault lines. The bus fault and feeder fault are distinguished by judging whether the contour coefficient exceeds the threshold value. Finally, the feeder line with the fault point is judged through the membership degree matrix obtained by clustering. The simulation results show the following points. ① The RCMDE curve of the fault line is different from that of the non-fault line, and the curves can be divided into two types. RCMDE can be used as the fault characteristic index of fault line. ② When the bus fault occurs, there are clusters with an average contour coefficient less than the threshold value in the clustering results. However, when feeder fault occurs, the contour coefficients of the clustering results are all greater than the threshold value. Under various fault scenarios, the coal mine power grid fault line selection method based on RCMDE and KFCM can realize correct line selection. The results show that its accuracy is not affected by factors such as fault line, fault location, fault closing angle and grounding resistance. ③ Under the conditions of noise disturbance, the fault line selection method based on RCMDE and KFCM can realize correct line selection in the case of low resistance grounding or high resistance grounding. And the method has a strong anti-interference capability. ④ Under the conditions of asynchronous sampling and reverse polarity of zero-sequence current transformer in the fault line, the method based on RCMDE and KFCM can still realize correct line selection. And the line selection result has high robustness.
-
0. 引言
目前在综采工作面已初步形成基于采煤机记忆截割和视频远程监测及人工协调相结合的智能开采模式[1-2]，但由于煤岩识别技术受限，记忆截割方法难以适应综采工作面煤层起伏变化较大的状况。为了实现采煤机自适应截割，基于综采工作面地质信息建立煤层三维模型来规划采煤机截割轨迹成为煤矿无人开采的研究热点和难点[3-5]。
目前煤层三维模型建立主要采用地质体三维建模方法，如采用钻孔及地震剖面等数据结合地质统计学构建静态煤层模型[6]、利用煤层边界约束和钻探数据块段构建煤层三维模型等[7]。这些煤层三维建模方法以静态建模为主，对动态采掘信息缺乏关注且煤层垂向分辨率较低。煤层地质属性决定了煤层三维模型需要动态修正，相关学者对煤层三维模型修正方法开展了深入研究。贾庆仁等[8]利用煤层边界的采样点和普通克里金法对煤层网格节点的高程及厚度属性进行插值，建立了初始煤层模型，根据开采数据的影响范围对初始煤层模型进行动态修正，提高了煤层三维模型的精度。修春华等[9]在建立煤层初始规则格网的基础上，深入分析利用离散钻孔采样数据进行煤层建模的误差来源，提出了基于点状、线状和面状地质数据对煤层三维模型进行动态修正的方法，将复杂地质断层设计为一种面状数据，提高了煤层模型的精度。刘万里等[10]提出在综采过程中利用最新探测的工作面激光扫描的顶底煤数据动态修正初始煤层模型，修正后的煤层误差绝对值小于0.2 m的区域比修正前提高了将近1倍。孙振明等[11]利用矿方原始数据构造煤层三维模型，随着工作面不断推进，基于实际开采获取的生产数据，通过膨胀搜索算法、样条曲面算法等关键技术，实现了煤层三维模型的局部动态修正。梁耍等[12]结合采煤机历史截割数据与初始煤层三维模型数据，提出了基于LSTM(Long-Short Term Memory, 长短期记忆)网络的煤层厚度动态预测方法，利用采煤机历史截割数据与初始煤层三维模型数据预测下一阶段未开采区煤层厚度，平均误差在0.05 m左右，为煤层垂向误差修正提供了技术支持。李娟莉等[13]基于采区煤层变化特征，提出结合双轨扫掠与加权融合的初始煤层DEM（Digital Elevation Model，数字高程模型）构建方法，引入采区内离散分布的煤层地质数据计算高程误差，拟合得到残差曲面并进行整体性偏移，实现了煤层DEM的动态精细修正。以上方法在煤层三维模型动态修正方面虽取得了一定的成果，但这些方法受制于物探技术，且大部分工作面地质条件较为复杂，煤层结构形态多样，导致煤层修正精度难以满足智能开采实际需求。
针对上述问题，笔者提出了一种综采工作面煤层三维模型动态修正方法。将已有的初始煤层三维模型静态数据与工作面动态采掘的采煤机截割数据融合，基于LSTM及其改进算法，利用上一回采阶段的煤层数据，预测下一阶段未开采区的煤层底板曲面和煤层厚度；利用双层循环的网格搜索方法自动调优预测算法的超参数，获取未开采区煤层底板和煤层厚度的高精度垂向分布数据，作为煤层三维模型修正值，从而局部动态修正未开采区的初始煤层三维模型。随着工作面不断开采，如此逐阶段推进，利用新获取的修正数据持续动态修正并更新初始煤层三维模型，从而提升初始煤层三维模型精度，使动态修正后的煤层三维模型能更准确地反映综采工作面实际煤层分布，为工作面智能开采提供技术支持。
1. 煤层三维模型动态修正原理
煤层三维模型动态修正原理如图1所示。
（1） 建立综采工作面初始煤层三维模型。采用震波CT(Computerized Tomography, 层析成像技术)精细物探煤层分布数据和矿方地质测量数据，利用三维地质建模方法，以ArcGIS软件为煤层建模工具，构建综采工作面初始煤层三维模型。
（2） 假定目前综采工作面处在第m回采阶段，从初始煤层三维模型中获取该阶段煤层顶底板数据，以及该阶段综采过程中新产生的采煤机滚筒上下截割信息。
（3） 获取动态采掘过程中采煤机截割轨迹。利用采煤机惯性导航系统、倾角传感器及采煤机两摇臂旋转编码器精确获取的动态采掘信息，经过相应计算得到采煤机截割轨迹。
（4） 煤层多源数据融合及预处理。融合初始煤层三维模型静态数据和动态采掘产生的采煤机截割数据，以采煤机截割数据作为煤层真实数据信息，提取煤层垂向坐标作为特征输入，划分数据集。
（5） 建立未开采区煤层预测算法。分别基于LSTM及其改进算法建立煤层预测算法，动态预测下一阶段未开采区的煤层底板形态和煤层厚度，采用双层循环嵌套的网格搜索方法自动调优煤层预测算法的超参数，获取未开采区煤层底板和煤层厚度的高精度垂向分布数据，作为煤层三维模型修正值。
（6） 局部动态修正煤层三维模型。利用第m回采阶段的数据预测第m+1回采阶段的煤层底板形态和煤层厚度分布作为煤层修正值，再将煤层底板和煤层厚度对应叠加生成煤层顶板修正值，从而局部动态修正未开采区的初始煤层三维模型。随着工作面不断开采，如此逐阶段推进，利用新获取的修正数据持续更新初始煤层三维模型，动态修正出高精度煤层三维模型。
2. LSTM预测算法
S. Hochreiter等[14]于1997年对传统的循环神经网络(Recurrent Neural Network, RNN)结构进行改进，提出了LSTM算法。A. Graves等[15]在LSTM算法基础上引入动态自循环，弥补了RNN存在的梯度消失和梯度爆炸等缺点。
LSTM算法的核心是通过使用门结构的记忆单元来存储输入的时序数据，其门结构分为遗忘门、输入门和输出门[15]。LSTM细胞的信息流动结构如图2所示。
![]()
图 2 LSTM细胞的信息流动结构Figure 2. Information flow structure of long-short term memory (LSTM) cell图2中xt与ht分别为t时刻的输入与隐藏状态，即短时记忆；Ct为t时刻的细胞状态，即长期记忆；σ为sigmoid函数，Tanh为tanh函数。3个门在LSTM细胞信息流动中的作用：遗忘门决定从细胞状态里去除一些信息，将t−1时刻细胞状态Ct−1选择性遗忘，保留下来的信息传递给当前t时刻的细胞状态Ct ；输入门包含sigmoid函数和tanh函数2个部分，其中sigmoid函数负责要更新的值，输出长期记忆，tanh函数创建一个候选值向量
$ \widetilde{{{\boldsymbol{C}}}_{t}} $ ，输出短时记忆，输入门决定xt以什么样的权重传递给Ct；输出门通过sigmoid函数控制t时刻的输入状态xt和t−1时刻的隐藏状态ht−1中哪些信息输出，再经过tanh函数处理，得到当前t时刻的隐藏状态ht。空间卷积长短期记忆网络( Convolutional Long-Short Term Memory, Conv LSTM)、编码−解码长短期记忆网络(Encoder-Decoder Long-Short Term Memory, Encoder-Decoder LSTM)[16]是在LSTM基础上的进一步改进。Conv LSTM引入了卷积操作，增强了算法对数据信息空间特性的提取能力；Encoder-Decoder LSTM则是利用循环网络读取序列数据，先将数据存放到固定维度的编码中，再利用另一RNN读取上一环节编码内数据信息，并将其解码为目标长度的数据。
LSTM，Conv LSTM，Encoder-Decoder LSTM算法在数据预处理时不需要过多地分析原始数据的隐藏关系，其通过网络神经元之间的相关权重来自动学习调整时间序列数据之间的关系，在处理时间序列数据中极具优势。煤层作为空间分布的一种层状地质实体，有较强的全局规律性。初始煤层三维模型数据及综采工作面动态生产时的采煤机历史截割轨迹数据可反映出煤层分布形态随煤层空间几何形态变化而不断变化的趋势，这些数据实质上是时间序列数据，因此，可用上述算法处理初始煤层三维模型数据和采煤机历史截割数据。
3. 数据获取与处理
首先获取煤层模型静态数据，即建立初始煤层三维模型，并将煤层模型数据处理成底板和煤层厚度栅格数据；然后利用采煤机惯性导航系统、倾角传感器等精确获取采煤机截割轨迹；最后对初始煤层三维模型数据和采煤机截割数据进行融合处理，提取有效特征并划分数据集。
3.1 初始煤层三维模型数据获取
本文以山西吕梁市某煤矿18201工作面为研究对象，利用震波CT精细物探数据和矿方地质测量数据建立初始煤层三维模型[17]。该模型以2000国家大地坐标系为参考坐标系，顶底板数据采用0.8 m×0.8 m的栅格点阵存储。以综采起始位为坐标原点，综采工作面方向为X轴，综采工作面推进方向为Y轴，重力加速度的反向为Z轴，建立综采工作面坐标系，如图3所示。
由于煤层数据是以栅格点阵坐标存储，每个坐标的X，Y轴值可以直接计算得到，所以本文只提取煤层Z轴值作为特征输入。提取前30刀煤层数据。用F表示初始煤层底板曲面数据，记为
${\boldsymbol{F}} = \{ {{\boldsymbol{f}}^1},{{\boldsymbol{f}}^2}, \cdots,{{\boldsymbol{f}}^{30}}\}$ ，f i为第i(i=1,2,···,30)刀底板数据${{\boldsymbol{f}}^i} = [z_{f1}^i,z_{f2}^i,\cdots, z_{f364}^i]$ ，其由364个Z轴值组成；用S表示初始煤层厚度数据，记为${\boldsymbol{S}} = \{ {{\boldsymbol{s}}^1},{{\boldsymbol{s}}^2}, \cdots ,{{\boldsymbol{s}}^{30}}\} $ ，si为第i刀煤层厚度数据，${{\boldsymbol{s}}^i} = [z_{s1}^i,z_{s2}^i,\cdots, z_{s364}^i]$ ，其由364个Z轴值组成。在工作面推进方向0~23.2 m（即前30刀）范围内，初始煤层厚度和底板曲面误差分布如图4所示。从图4（a）可看出，初始煤层厚度误差主要分布在0.35~0.45 m，平均误差为0.40 m；从图4（b）可看出，初始煤层底板曲面误差主要分布在0.15~0.25 m，平均误差为0.20 m。3.2 采煤机截割轨迹数据精确获取
基于18201综采工作面，利用采煤机机载定位定姿装置测量动态采掘数据，结合采煤机控制器记录数据，最终获取采煤机历史截割轨迹[18]，部分截割轨迹如图5所示。采用反距离加权法[19]，将截割轨迹曲线处理成与初始煤层同类型的栅格点阵数据。用D表示采煤机下截割轨迹数据，记为
${\boldsymbol{D}} = \{ {{\boldsymbol{d}}^1},{{\boldsymbol{d}}^2}, \cdots , {{\boldsymbol{d}}^{30}}\} $ ，di第i刀下截割数据，$ {{\boldsymbol{d}}^i} = [z_{d1}^i,z_{d2}^i,\cdots,z_{d364}^i] $ ，其由364个Z轴值组成。相同位置的上下截割曲面沿Z轴做差，获得采煤机采高分布，采高数据用H表示。采煤机截割轨迹在动态采掘过程中不断产生，本文以采煤机截割轨迹数据作为煤层数据真实值。3.3 数据预处理
本文提取工作面推进方向0~23.2 m（即前30刀）的采煤机截割轨迹数据和初始煤层三维模型数据作为数据集，将数据集以2∶1划分为训练集和测试集。训练集由前20刀采煤机下截割数据和初始煤层底板数据构成；测试集由21—30刀采煤机下截割数据和初始煤层底板数据构成，截割数据作为标签序列数据。煤层底板曲面预测的数据组合方式见表1。煤层厚度预测的数据组合方式与煤层底板曲面预测的数据组合方式类似，训练集由前20刀采煤机采高数据和初始煤层厚度数据构成；测试集由21—30刀采高数据和初始煤层厚度数据构成。
表 1 煤层底板曲面预测的数据组合方式Table 1. Prediction data combination mode of coal seam floor curved surface类型 序号 输入序列数据 标签序列数据 训练集 1 f 1 d1 2 f 2 d2 $\vdots $ $\vdots $ $\vdots $ 20 f 20 d20 测试集 1 f 21 d21 2 f 22 d22 $\vdots $ $\vdots $ $\vdots $ 10 f 30 d30 4. 煤层三维模型修正值获取
通过数据获取和预处理将初始煤层三维模型顶底板数据及采煤机截割数据处理成相同类型的栅格点阵数据，并提取煤层底板和煤层厚度Z轴值作为未开采区的煤层底板曲面预测和煤层厚度预测算法的特征输入，精确预测并获取下一阶段煤层三维模型修正值。
4.1 煤层修正值预测算法结构设计
本文通过线性堆叠网络层的方式搭建了3种煤层三维模型预测算法，分别为LSTM，Conv LSTM，Encoder-Decoder LSTM算法。LSTM预测算法结构如图6所示，其包括LSTM层和Dense层。为了便于提取输入信息的空间特征，Conv LSTM算法在单元输入处添加了卷积操作，算法结构包括3个网络层，分别为Conv LSTM层、Flatten层和Dense层，在Conv LSTM层中设置卷积核数为64，卷积核大小为(3, 3)。Encoder-Decoder LSTM算法的超参数默认值设定与LSTM相同，算法结构包括4个网络层，分别为LSTM层、Repeat Vector层、LSTM层及Time Distributed层。
4.2 煤层底板曲面修正值精确预测
本文采用煤层底板预测值与煤层底板真实值的平均绝对误差(Mean Absolute Error, MAE)来评估预测算法的预测能力。MAE能够反映煤层底板曲面预测的整体效果，MAE越小说明预测效果越好。
为避免手动调参时预测算法可能会出现结果局部最优的情况，本文采用双层嵌套循环的网格搜索方法对预测算法的超参数进行自动调优，各超参数候选值见表2。
表 2 超参数候选值Table 2. Candidate values of hyperparameters超参数 候选值 输入输出序列步长(Steps) (4:1), (3:1), (2:1), (1:1) 隐藏层神经元个数(Units) 100, 90, 70, 50, 30, 20, 10 激活函数(Activation) ReLU, Sigmoid, Tanh, Softplus 优化器(Optimizer) SGD, Adadelta, RMSProp, Adagrad, Adam 损失函数(Loss) MAE 训练周期(Epoch) 10, 30, 50, 80, 100, 150, 200 超参数优化流程如图7所示，外层循环遍历各个超参数，内层循环遍历各超参数候选值。得到优化结果见表3。在煤层底板曲面预测方面，Conv LSTM算法预测结果的MAE最小，为0.074 m，其算法的输入输出序列步长为(1, 1)，隐藏层神经元个数为10，激活函数为Softplus，优化器为Adagrad，训练周期为100；LSTM算法和Encoder-Decoder LSTM算法预测结果的MAE分别为0.594 ，0.323 m。
表 3 煤层底板曲面修正值预测算法超参数优化结果Table 3. Hyperparameters optimization results of prediction algorithms for coal seam floor curved surface correction value预测算法 [Steps, Units, Activation,
Optimizer, Epoch]MAE/m LSTM [(1, 1), 20, Softplus, Adadelta, 100] 0.594 Conv LSTM [(1, 1), 10, Softplus, Adagrad, 100] 0.074 Encoder-Decoder LSTM [(1, 1), 20, Softplus, Adagrad, 50] 0.323 为进一步对比3种算法对煤层底板曲面形态的预测能力，将工作面推进方向16.8 m（即采煤机第22刀）处的煤层底板预测值与真实值进行对比，如图8所示。可看出Conv LSTM算法预测值与真实值高度吻合；LSTM算法预测值在X处于0~50 m范围内波动较大；Encoder-Decoder LSTM算法预测值在X处于200~250 m范围内产生与真实值相差较大的异常值。总体来看，Conv LSTM算法在煤层底板曲面形态预测上更具优势。
![]()
图 8 工作面推进方向16.8 m处煤层底板曲面修正值预测结果Figure 8. Prediction results of coal seam floor curved surface correction value at location of 16.8 m in advancing direction of working face4.3 煤层厚度修正值精确预测
煤层厚度预测与煤层底板曲面预测采用的算法相同，评估方法不同。由于煤层厚度在实际工况下变化比底板曲面变化更加明显，而均方根误差(Root Mean Squared Error, RMSE)在处理波动性变化数据方面具有优势，所以选用RMSE来评估煤层厚度预测算法的优劣。
同样采取双层嵌套循环的网格搜索方法对煤层厚度预测算法进行自动调参，得到的优化结果见表4。可看出LSTM，Conv LSTM，Encoder-Decoder LSTM算法的RMSE均较小，分别为0.051，0.051，0.049 m，表明3种算法对煤层厚度预测的整体效果较好。
表 4 煤层厚度预测算法超参数优化结果Table 4. Hyperparameter optimization results of coal seam thickness prediction algorithms预测算法 [Steps, Units, Activation,
Optimizer, Epoch]RMSE/m LSTM [(1, 1), 100, ReLU, Adagrad, 100] 0.051 Conv LSTM [(1, 1), 100，Softplus，Adagrad，90] 0.051 Encoder-Decoder LSTM [(1, 1), 100，ReLU，Adagrad，90] 0.049 为进一步对比各算法对煤层厚度的预测能力，将工作面推进方向16.8 m处的煤层厚度预测值与真实值进行对比，如图9所示。
![]()
图 9 工作面推进方向16.8 m处煤层厚度修正值预测结果Figure 9. Prediction results of coal seam thickness correction value at location of 16.8 m in advancing direction of working face从图9可看出，3种算法均能较好地预测出下一阶段煤层厚度；当X约为124 ，220.8 m时，煤层厚度预测误差较大，约为0.15 m，其余部分的误差均较小。对比分析得出Encoder-Decoder LSTM算法的预测值更接近真实值，且更稳定，预测效果更好。
4.4 煤层顶板修正值获取
通过煤层底板和煤层厚度修正值精确预测，可以得出Conv LSTM算法对煤层底板曲面的预测效果最好，Encoder-Decoder LSTM算法在煤层厚度预测方面更具优势。将煤层底板曲面和煤层厚度预测结果叠加，生成煤层顶板曲面，作为下一阶段未开采区的煤层顶板修正值。
5. 实验验证
以山西吕梁市某煤矿18201工作面煤层三维模型为例，对修正方法的有效性进行实验验证。在工作面推进方向16~23.2 m范围内，初始煤层三维模型的底板曲面垂向平均误差在0.20 m左右，煤层厚度垂向误差在0.40 m左右。用煤层底顶板的修正值局部修正工作面初始煤层三维模型。修正后的煤层底顶板误差分布如图10所示。可看出修正后煤层底板误差主要分布在0.10 m以下，平均误差为0.0685 m；修正后的煤层顶板误差主要分布在0.15 m以下，平均误差为0.076 m。
![]()
图 10 煤层三维模型修正后的底顶板误差分布Figure 10. Error distribution of floor and top of coal seam 3D model after correction在工作面推进方向16~23.2 m范围内，初始煤层三维模型修正前后的误差分布如图11所示。从图11（a）可看出，初始煤层三维模型修正前，煤层底板误差主要分布在0.15~0.30 m，修正后误差主要分布在0~0.10 m；初始煤层底板误差在0.15~0.20，0.20~0.30 m的区域分别占总区域的34.5%，40.2%，模型修正后误差分别降低到6%，1.2%。从图11（b）可看出，初始煤层三维模型修正前，煤层顶板误差主要分布在0.20~0.30 m，修正后误差主要分布在0~0.15 m；初始煤层顶板误差在0.15~0.20，0.20~0.30 m的区域分别占总区域的33.6%，49.7%，模型修正后分别降低到6.3%，2.1%。
![]()
图 11 煤层三维模型修正前后底顶板预测误差分布占比Figure 11. Proportion of error distribution of floor and top prediction before and after coal seam 3D model correction修正后的初始煤层三维模型误差大大降低，证明了本文提出的动态修正方法的有效性。随着煤层不断开采，在综采工作面推进过程中持续动态更新初始煤层三维模型，提高模型精度，为下一阶段未开采区提供较为精确的煤层分布数据。
6. 结论
（1） 提出了一种综采工作面煤层三维模型动态修正方法，融合初始煤层三维模型静态数据和采掘获取的采煤机截割轨迹信息，基于LSTM及其改进算法，利用上一回采阶段的煤层信息精确预测下一阶段未开采区的煤层分布数据，作为煤层三维模型修正值，动态修正未开采区的煤层三维模型。
（2） 基于LSTM，Conv LSTM，Encoder-Decoder LSTM预测算法分别对未开采区的煤层底板曲面修正值及煤层厚度修正值进行预测，再利用双层嵌套循环的网格搜索方法自动调优预测算法的超参数。Conv LSTM算法对煤层底板曲面的动态预测效果最好，其MAE为0.074 m；Encoder-Decoder LSTM算法在煤层厚度动态预测中表现最佳，其RMSE为0.049 m。
（3） 以山西吕梁市某煤矿18201工作面煤层三维模型为例，在工作面推进方向16~23.2 m范围内，利用动态修正方法对煤层三维模型进行实验验证。结果表明修正后煤层底板平均误差为0.0685 m，煤层顶板平均误差为0.076 m，相较于初始煤层三维模型底板平均误差0.20 m、煤层厚度垂向平均误差0.40 m大大降低，证实了动态修正方法可以有效提升煤层三维模型的精度，可精确反映工作面实际煤层分布，为智能开采提供高精度煤层三维模型。
-
![]()
图 1 基于RCMDE和KFCM的故障选线流程
Figure 1. Fault line selection process based on RCMDE and KFCM
![]()
图 2 煤矿电网单相接地故障仿真模型
Figure 2. Simulation model of single phase grounding fault in coal mine power grid
表 1 电缆线路参数
Table 1 Parameter of cable line
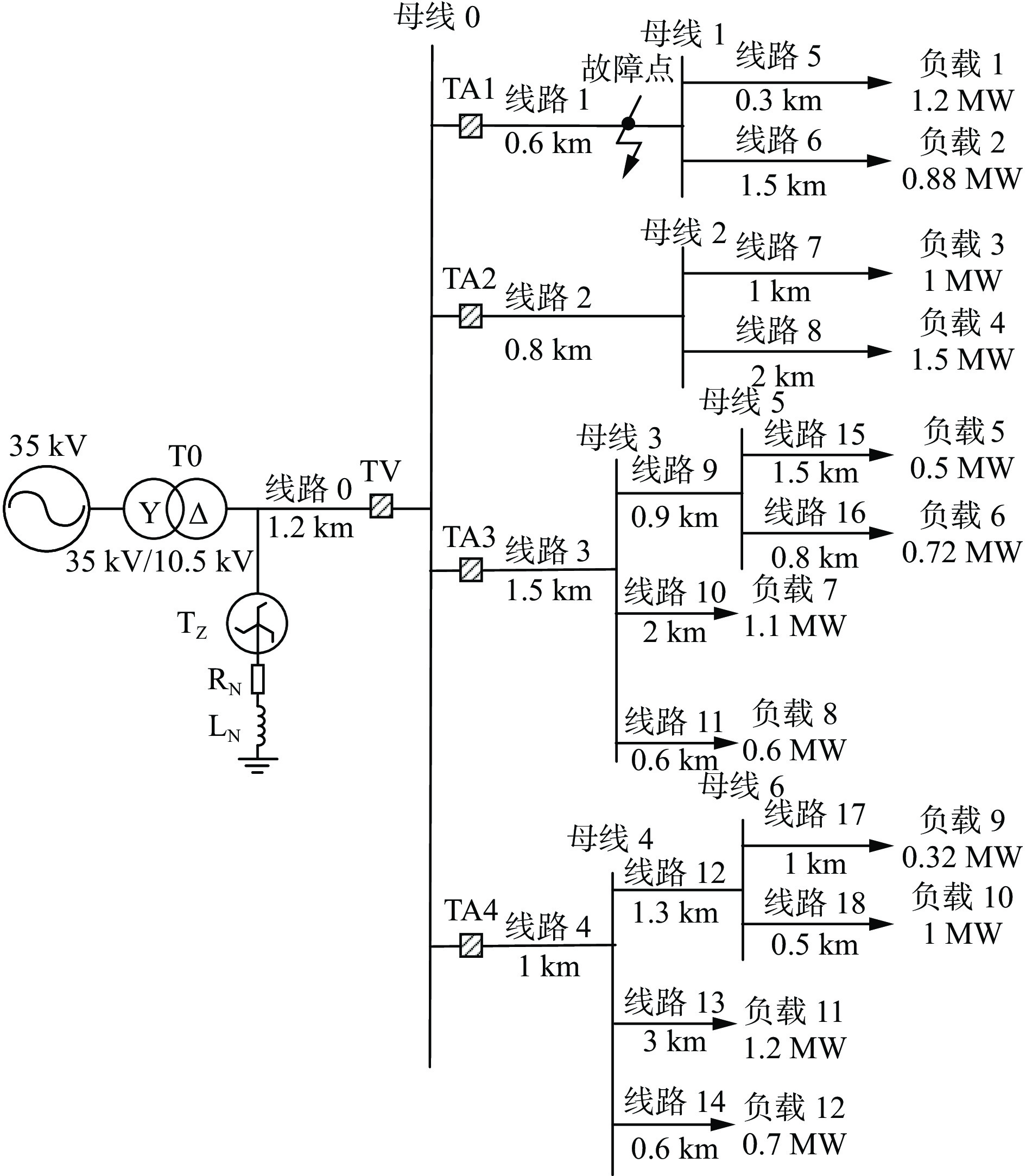
相序 单位长度电阻/ (Ω·km−1) 单位长度电感/ (mH·km−1) 单位长度电容/ (μF·km−1) 正序 0.270 0.255 0.339 零序 2.700 1.019 0.280 
下载: 导出CSV
表 2 所提方法在各类故障场景下的选线结果
Table 2 Line selection results of the proposed method in various fault scenarios
故障线路 故障位置/ km α0/ (°) Rf / Ω 隶属度矩阵U 各簇平均轮廓系数 选线结果 线路1 0.2 0 0.001 $\left[ {\begin{array}{*{20}{l}} {\bf {{{1}}{{.000\;0}}} }&{{{0}}{{.003\;0}}}&{{{0}}{{.002\;4}}}&{{{0}}{{.000\;9}}} \\[2.9pt] {{{0}}{{.000\;0}}}&{\bf {{{0}}{{.997\;0}}} }&{\bf {{{0}}{{.997\;6}}} }&{\bf {{{0}}{{.999\;1}}} } \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{1}} \\[2.9pt] {{{0}}{{.994\;7}}} \end{array}} \right] $ 线路1 0.3 60 50 $\left[ {\begin{array}{*{20}{l}} {{{0}}{{.000\;0}}}&{\bf {{{0}}{{.998\;3}}} }&{\bf {{{0}}{{.996\;9}}} }&{\bf {{{0}}{{.999\;1}}} } \\[2.9pt] {\bf {{{1}}{{.000\;0}}} }&{{{0}}{{.001\;7}}}&{{{0}}{{.003\;1}}}&{{{0}}{{.000\;9}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.996\;0}}} \\[2.9pt] {{1}} \end{array}} \right] $ 线路1 0.4 90 5 000 $\left[ {\begin{array}{*{20}{l}} {{{0}}{{.000\;0}}}&{\bf {{{0}}{{.999\;4}}} }&{\bf {{{0}}{{.999\;7}}} }&{\bf {{{0}}{{.999\;8}}} } \\[2.9pt] {\bf {{{1}}{{.000\;0}}} }&{{{0}}{{.000\;6}}}&{{{0}}{{.000\;3}}}&{{{0}}{{.000\;2}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.999\;1}}} \\[2.9pt] {{1}} \end{array}} \right] $ 线路1 线路3 0.3 75 50 $\left[ {\begin{array}{*{20}{l}} {{{0}}{{.016\;8}}}&{{{0}}{{.000\;7}}}&{\bf {{{0}}{{.998\;0}}} }&{{{0}}{{.001\;1}}} \\[2.9pt] {\bf {{{0}}{{.983\;2}}} }&{\bf {{{0}}{{.999\;3}}} }&{{{0}}{{.002\;0}}}&{\bf {{{0}}{{.998\;9}}} } \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} 1 \\[2.9pt] {{{0}}{{.986\;1}}} \end{array}} \right] $ 线路3 0.7 15 800 $\left[ {\begin{array}{*{20}{l}} {{{0}}{{.001\;3}}}&{{{0}}{{.001\;3}}}&{\bf {{{1}}{{.000\;0}}} }&{{{0}}{{.000\;8}}} \\[2.9pt] {\bf {{{0}}{{.998\;7}}} }&{\bf {{{0}}{{.998}}\;7} }&{{{0}}{{.000\;0}}}&{\bf {{{0}}{{.999\;2}}} } \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{1}} \\[2.9pt] {{{0}}{{.999\;6}}} \end{array}} \right] $ 线路3 1.2 45 6 000 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.999\;3}}} }&{\bf {{{0}}{{.999\;4}}} }&{{{0}}{{.000\;0}}}&{\bf {{{0}}{{.998\;8}}} } \\[2.9pt] {{{0}}{{.000\;7}}}&{{{0}}{{.000\;6}}}&{\bf {{{1}}{{.000}} \;0} }&{{{0}}{{.001\;2}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.998\;2}}} \\[2.9pt] 1 \end{array}} \right] $ 线路3 母线0 — 0 5 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.936\;0}}} }&{{{0}}{{.354\;9}}}&{{{0}}{{.045\;3}}}&{{{0}}{{.041\;3}}} \\[2.9pt] {{{0}}{{.064\;0}}}&{\bf {{{0}}{{.645\;1}}} }&{\bf {{{0}}{{.954\;7}}} }&{\bf {{{0}}{{.958\;7}}} } \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{1}} \\[2.9pt] {{{0}}{{.712\;9}}} \end{array}} \right] $ 母线0 — 45 200 $\left[ {\begin{array}{*{20}{l}} {{{0}}{{.216\;4}}}&{\bf {{{0}}{{.826\;6}}} }&{\bf {{{0}}{{.707\;4}}} }&{\bf {{{0}}{{.804\;3}}} } \\[2.9pt] {\bf {{{0}}{{.783\;6}}} }&{{{0}}{{.173\;4}}}&{{{0}}{{.292\;6}}}&{{{0}}{{.195\;7}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.739\;3}}} \\[2.9pt] {{1}} \end{array}} \right] $ 母线0 — 90 4 000 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.932\;3}}} }&{{{0}}{{.426\;9}}}&{{{0}}{{.101\;7}}}&{{{0}}{{.016\;5}}} \\[2.9pt] {{{0}}{{.067\;7}}}&{\bf {{{0}}{{.573\;1}}} }&{\bf {{{0}}{{.898\;3}}} }&{\bf {{{0}}{{.983\;5}}} } \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{1}} \\[2.9pt] {{{0}}{{.640\;7}}} \end{array}} \right] $ 母线0
下载: 导出CSV
表 3 噪声干扰下的选线结果
Table 3 Line selection results with noise disturbance
Rf / Ω 隶属度
矩阵U各簇平均
轮廓系数选线
结果0.001 $\left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.984\;1}}} }&{{{0}}{{.000\;2}}}&{\bf {{{0}}{{.984\;0}}} }&{\bf {{{0}}{{.997\;7}}} } \\ {{{0}}{{.015\;9}}}&{\bf {{{0}}{{.999\;8}}} }&{{{0}}{{.016\;0}}}&{{{0}}{{.002\;3}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.966\;1}}} \\ {{1}} \end{array}} \right] $ 线路2 100 $\left[ {\begin{array}{*{20}{l}} {{\bf{0}}{\bf{.995\;6}}}&{{{0}}{{.022\;3}}}&{\bf {{{0}}{{.991\;5}}} }&{\bf {{{0}}{{.981\;8}}} } \\ {{{0}}{{.004\;4}}}&{\bf {{{0}}{{.977\;7}}} }&{{{0}}{{.008\;5}}}&{{{0}}{{.018\;2}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.985\;0}}} \\ {{1}} \end{array}} \right] $ 线路2 10000 $\left[ {\begin{array}{*{20}{l}} {{\bf{0}}{\bf{.966\;7}}}&{{{0}}{{.001\;2}}}&{\bf {{{0}}{{.989\;3}}} }&{\bf {{{0}}{{.978\;5}}} } \\ {{{0}}{{.033}}\; {3}}&{\bf {{{0}}{{.998\;8}}} }&{{{0}}{{.010\;7}}}&{{{0}}{{.021\;5}}} \end{array}} \right]$ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.937\;8}}} \\ {{1}} \end{array}} \right] $ 线路2
下载: 导出CSV
表 4 采样不同步时的选线结果
Table 4 Line selection results under asynchronous sampling
Rf / Ω 隶属度
矩阵U各簇平均
轮廓系数选线
结果5 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.985\;6}}} }&{\bf {{{0}}{{.984\;5}}} }&{\bf {{{0}}{{.997\;7}}} }&{{{0}}{{.000\;2}}} \\ {{{0}}{{.014\;4}}}&{{{0}}{{.015\;5}}}&{{{0}}{{.002\;3}}}&{\bf {{{0}}{{.999\;8}}} } \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.968\;1}}} \\ {{1}} \end{array}} \right] $ 线路4 800 $ \left[ {\begin{array}{*{20}{l}} {{{0}}{{.000\;3}}}&{{{0}}{{.000\;5}}}&{{{0}}{{.000\;6}}}&{\bf {{{1}}{{.000\;0}}} } \\ {\bf {{{0}}{{.999\;7}}} }&{\bf {{{0}}{{.999\;5}}} }&{\bf {{{0}}{{.999\;4}}} }&{{{0}}{{.000\;0}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{1}} \\ {{{0}}{{.999\;6}}} \end{array}} \right] $ 线路4 5 000 $ \left[ {\begin{array}{*{20}{l}} {{{0}}{{.011\;7}}}&{{{0}}{{.013\;2}}}&{{{0}}{{.006\;7}}}&{\bf {{{0}}{{.946\;9}}} } \\ {\bf {{{0}}{{.988\;3}}} }&{\bf {{{0}}{{.986\;8}}} }&{\bf {{{0}}{{.993\;3}}} }&{{{0}}{{.053\;1}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} 1 \\ {{{0}}{{.998\;1}}} \end{array}} \right] $ 线路4
下载: 导出CSV
表 5 极性反接时的选线结果
Table 5 Line selection results with anti-polarity
Rf / Ω 隶属度
矩阵U各簇平均
轮廓系数选线
结果0.001 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.995\;0}}} }&{\bf {{{0}}{{.994\;8}}} }&{{{0}}{{.012\;6}}}&{\bf {{{0}}{{.995\;4}}} } \\ {{{0}}{{.005\;0}}}&{{{0}}{{.005\;2}}}&{\bf {{{0}}{{.987\;4}}} }&{{{0}}{{.004\;6}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.999\;9}}} \\ 1 \end{array}} \right] $ 线路3 60 $ \left[ {\begin{array}{*{20}{l}} {\bf {{{0}}{{.997\;9}}} }&{\bf {{{0}}{{.999\;0}}} }&{{{0}}{{.000\;0}}}&{\bf {{{0}}{{.998\;7}}} } \\ {{{0}}{{.002\;1}}}&{{{0}}{{.001\;0}}}&{\bf {{{1}}{{.000\;0}}} }&{{{0}}{{.001\;3}}} \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.998\;3}}} \\ {{1}} \end{array}} \right] $ 线路3 6 000 $ \left[ {\begin{array}{*{20}{l}} {{{0}}{{.000\;6}}}&{{{0}}{{.000\;8}}}&{\bf {{{0}}{{.999\;9}}} }&{{{0}}{{.000\;9}}} \\ {\bf {{{0}}{{.999\;4}}} }&{\bf {{{0}}{{.999\;2}}} }&{{{0}}{{.000\;1}}}&{\bf {{{0}}{{.999\;1}}} } \end{array}} \right] $ $ \left[ {\begin{array}{*{20}{c}} {{{0}}{{.999\;1}}} \\ {{1}} \end{array}} \right] $ 线路3
下载: 导出CSV
-
[1] 高宏杰,赵建文,郭秀才. 煤矿电网单相漏电故障区段自动定位探索[J]. 工矿自动化,2021,47(5):106-111. GAO Hongjie,ZHAO Jianwen,GUO Xiucai. Research on automatic location of single-phase leakage fault zone in coal mine power network[J]. Industry and Mine Automation,2021,47(5):106-111.
[2] LIU Penghui,DU Shaotong,SUN Kang,et al. Single-line-to-ground fault feeder selection considering device polarity reverse installation in resonant grounding system[J]. IEEE Transactions on Power Delivery,2021,36(4):2204-2212. DOI: 10.1109/TPWRD.2020.3022422
[3] NIU Lin,WU Guiqing,XU Zhangsheng. Single-phase fault line selection in distribution network based on signal injection method[J]. IEEE Access,2021,9:21567-21578. DOI: 10.1109/ACCESS.2021.3055236
[4] 张利,杨以涵,杨秀媛,等. 移动式比相法配电网接地故障定位研究[J]. 中国电机工程学报,2009,29(7):91-97. DOI: 10.3321/j.issn:0258-8013.2009.07.015 ZHANG Li,YANG Yihan,YANG Xiuyuan,et al. Method of mobile phase-comparison for fault location of distribution network[J]. Proceeding of the CSEE,2009,29(7):91-97. DOI: 10.3321/j.issn:0258-8013.2009.07.015
[5] 孙其东,张开如,刘建,等. 基于五次谐波和小波重构能量的配电网单相接地故障的选线方法研究[J]. 电测与仪表,2016,53(16):1-4. DOI: 10.3969/j.issn.1001-1390.2016.16.001 SUN Qidong,ZHANG Kairu,LIU Jian,et al. Research on single-phase fault earth fault line selection method for the distribution network based on fifth harmonics and wavelet reconstruction[J]. Electrical Measurement & Instrumentation,2016,53(16):1-4. DOI: 10.3969/j.issn.1001-1390.2016.16.001
[6] 栾晓明,武守远,贾春娟,等. 基于改进零序导纳法的单相接地故障选线原理[J]. 电网技术,2022,46(1):353-360. DOI: 10.13335/j.1000-3673.pst.2021.0425 LUAN Xiaoming,WU Shouyuan,JIA Chunjuan,et al. Fault line selection principle of single-phase-to-ground fault based on improved zero-sequence admittance[J]. Power System Technology,2022,46(1):353-360. DOI: 10.13335/j.1000-3673.pst.2021.0425
[7] 束洪春,龚振,田鑫萃,等. 基于故障特征频带及形态谱的单相接地故障选线[J]. 电网技术,2019,43(3):1041-1053. SHU Hongchun,GONG Zhen,TIAN Xincui,et al. Single line-to-ground fault line selection based on fault characteristic frequency band and morphological spectrum[J]. Power System Technology,2019,43(3):1041-1053.
[8] 魏向向,温渤婴. 基于2阶累加生成相关性的谐振接地系统故障选线方法[J]. 电网技术,2017,41(5):1674-1682. WEI Xiangxiang,WEN Boying. A novel fault line detection method based on 2-order accumulated generating operation correlation analysis for resonant earthed system[J]. Power System Technology,2017,41(5):1674-1682.
[9] 于群,尚雪丽. 一种矿井漏电保护选线方法[J]. 工矿自动化,2020,46(11):17-22. YU Qun,SHANG Xueli. A line selection method of mine leakage protection[J]. Industry and Mine Automation,2020,46(11):17-22.
[10] 邓丰,梅龙军,唐欣,等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报,2021,36(13):2861-2870. DENG Feng,MEI Longjun,TANG Xin,et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society,2021,36(13):2861-2870.
[11] 王建元,朱永涛,秦思远. 基于方向行波能量的小电流接地系统故障选线方法[J]. 电工技术学报,2021,36(19):4085-4096. WANG Jianyuan,ZHU Yongtao,QIN Siyuan. Fault line selection method for small current grounding system based on directional traveling wave energy[J]. Transactions of China Electrotechnical Society,2021,36(19):4085-4096.
[12] 陈奎,韦晓广,陈景波,等. 基于样本数据处理和ADABOOST的小电流接地故障选线[J]. 中国电机工程学报,2014,34(34):6228-6237. CHEN Kui,WEI Xiaoguang,CHEN Jingbo,et al. Fault line detection using sampled data processing and ADABOOST for small current grounding system[J]. Proceeding of the CSEE,2014,34(34):6228-6237.
[13] 殷浩然,苗世洪,郭舒毓,等. 基于S变换相关度和深度学习的配电网单相接地故障选线新方法[J]. 电力自动化设备,2021,41(7):88-96. DOI: 10.16081/j.epae.202105028 YIN Haoran,MIAO Shihong,GUO Shuyu,et al. Novel method for single-phase grounding fault line selection in distribution network based on S-transform correlation and deep learning[J]. Electric Power Automation Equipment,2021,41(7):88-96. DOI: 10.16081/j.epae.202105028
[14] 郝帅,张旭,马瑞泽,等. 基于改进GoogLeNet的小电流接地系统故障选线方法[J]. 电网技术,2022,46(1):361-368. HAO Shuai,ZHANG Xu,MA Ruize,et al. Fault line selection method for small current grounding system based on improved GoogLeNet[J]. Power System Technology,2022,46(1):361-368.
[15] HAMED A,MOSTAFA R,DANI A,et al. Refined composite multiscale dispersion entropy and its application to biomedical signals[J]. IEEE Transactions on Biomedical Engineering,2017,64(12):2872-2879. DOI: 10.1109/TBME.2017.2679136
[16] ROSTAGHI M,AZAMI H. Dispersion entropy:a measure for time-series analysis[J]. IEEE Signal Processing Letters,2016,23(5):610-614. DOI: 10.1109/LSP.2016.2542881
[17] 何玉灵,孙凯,王涛,等. 基于变分模态分解与精细复合多尺度散布熵的发电机匝间短路故障诊断[J]. 电力自动化设备,2021,41(3):164-172. DOI: 10.16081/j.epae.202101014 HE Yuling,SUN Kai,WANG Tao,et al. Fault diagnosis of generator interturn short circuit fault based on variational mode decomposition and refined composite multiscale dispersion entropy[J]. Electric Power Automation Equipment,2021,41(3):164-172. DOI: 10.16081/j.epae.202101014
[18] 李从志,郑近德,潘海洋,等. 基于精细复合多尺度散布熵与支持向量机的滚动轴承故障诊断方法[J]. 中国机械工程,2019,30(14):1713-1719,1726. LI Congzhi,ZHENG Jinde,PAN Haiyang,et al. Fault diagnosis method of rolling bearings based on refined composite multiscale dispersion entropy and support vector machine[J]. China Mechanical Engineering,2019,30(14):1713-1719,1726.
[19] LIU Jingwei,XU Meizhi. Kernelized fuzzy attribute C-means clustering algorithm[J]. Fuzzy Sets and Systems,2008,159(18):2428-2445. DOI: 10.1016/j.fss.2008.03.018
[20] 郭谋发. 配电网单相接地故障人工智能选线[M]. 北京: 中国水利水电出版社, 2020. GUO Moufa. Artificial intelligence line selection of single-phase grounding fault in distribution network[M]. Beijing: China Water & Power Press, 2020.
[21] 卢丹. 基于WAMS的矿井高压电网单相接地故障选线及定位方法研究[D]. 北京: 中国矿业大学（北京）, 2015. LU Dan. Study on single-phase earth fault line detection and fault location method of coal mine high-voltage grid base on WAMS[D]. Beijing: China University of Mining & Technology-Beijing, 2015.
-
期刊类型引用(1)
1. 刘溯奇，颜雪盈，刘玉萍. 无线电能传输系统全桥逆变器性能优化研究. 现代电子技术. 2024(18): 89-94 . 
百度学术
其他类型引用(7)
计量
- 文章访问数: 152
- HTML全文浏览量: 55
- PDF下载量: 30
- 被引次数: 8
