Prediction model of water inrush in coal mine based on IWOA-SVM
-
摘要: 针对传统煤矿突水预测算法易陷入局部最优、预测结果准确率低及速度慢等问题,提出一种基于改进鲸鱼优化算法(IWOA)−支持向量机(SVM)的煤矿突水预测模型。IWOA从鲸鱼种群初始化、调节因子非线性化及随机差分进化(DE)3个方面入手对鲸鱼优化算法(WOA)进行改进:使用Tent映射初始化鲸鱼种群,提高鲸鱼种群寻找到最优猎物的可能性;通过调节因子非线性变化策略,提升算法在迭代前期的全局搜索能力及迭代后期的局部搜索能力,从而加快收敛速度;引入DE算法的变异、交叉、选择操作,以增强WOA的全局搜索能力。利用IWOA对SVM模型进行参数优化,将影响煤矿突水的水压、隔水层厚度、煤层倾角、断层落差、断层与工作面距离、采高共6个影响因素作为模型的输入特征向量,突水与安全2种突水结果作为模型的输出向量,以突水预测结果与实际结果间的误差最小化为目标建立目标函数,得到基于IWOA−SVM的煤矿突水预测模型。实验结果表明:与粒子群优化算法、DE算法、WOA相比,IWOA的预测准确率最高,标准误差最小,且收敛速度快,鲁棒性好;IWOA−SVM的突水预测准确率达到100%,与传统的突水系数法、SVM、WOA−SVM相比,IWOA−SVM表现出更高的准确率和稳定性。Abstract: The traditional prediction algorithm of water inrush in coal mine is easy to fall into local optimum, the prediction results accuracy is low and the speed is slow. In order to solve the above problems, a prediction model of water inrush in coal mine based on improved whale optimization algorithm (IWOA) and support vector machine (SVM) is proposed. IWOA improves the whale optimization algorithm (WOA) from three aspects, whale population initialization, nonlinear adjustment factor and random differential evolution (DE). Tent mapping is used to initialize the whale population to improve the possibility of the whale population finding the optimal prey. The non-linear change strategy of the adjustment factor is applied to improve the global search capability of the algorithm in the early stage of the iteration and the local search capability in the later stage of the iteration so as to speed up the convergence speed. The mutation, crossover and selection operations of DE algorithm are introduced to enhance the global search capability of WOA. The parameters of SVM model are optimized by IWOA. The six factors affecting water inrush in coal mine, including water pressure, thickness of aquiclude, dip angle of coal seam, fault drop, distance between fault and working face and mining height are taken as the input characteristic vectors of the model. The two water inrush results of water inrush and safety are taken as the output vectors. The objective function is established to minimize the error between the water inrush prediction results and the actual results, and the coal mine water inrush prediction model based on IWOA−SVM is obtained. The experimental results show that IWOA has the highest prediction accuracy, minimum standard error, fast convergence and good robustness compared with particle swarm optimization, DE algorithm and WOA. The accuracy of water inrush prediction of IWOA−SVM is 100%. Compared with the traditional water inrush coefficient method, SVM and WOA−SVM, IWOA−SVM shows higher accuracy and stability.
-
0. 引言
矿井突水作为严重威胁煤矿生产安全的主要矿井灾害之一,一旦发生会给矿区造成严重的经济损失和人员伤亡[1]。对煤层突水进行预测,可在突水事故发生之前及时采取措施,从而减少突水事故,更有效地保障煤矿生产安全。传统的突水预测方法主要包括突水系数法、阻水系数法及脆弱性指数法等[2-3]。这些方法已被广泛应用于突水预测中,但仍存在缺陷,如突水系数法和阻水系数法考虑的因素都较少且计算精度低,脆弱性指数法需要多种属性的支持且对原始数据的要求较高。
近年来,机器学习方法被越来越多地用于解决煤矿突水预测问题。潘辉等[4]针对底板突水非线性特征,利用粒子群优化(Particle Swarm Optimization,PSO) 算法优化BP神经网络,建立了底板突水预测模型,但BP神经网络训练依赖大量数据,对小样本突水事件的预测精度偏低。宋国娟[5]将PSO算法与极限学习机结合进行突水预测,Wang Ge等[6]利用PSO算法和蚁群优化算法分别对极限学习机进行优化,建立突水预测模型,但这2种算法在寻优时收敛速度都较慢。师煜等[7]利用遗传算法和PSO算法优化随机森林回归模型,提高了突水预测精度。李颖[8]针对非线性、小样本的底板突水问题,首次将支持向量机(Support Vecor Machine,SVM)模型用于底板突水预测,通过实验验证了该模型的有效性。张风达等[9]采用PSO算法优化支SVM参数,提高了突水预测精度。智能群体算法一定程度上改善了机器学习模型参数选择盲目的问题,但常用的智能优化算法如PSO算法、蚁群算法、果蝇优化算法[10]、遗传算法等仍存在参数设置较多、收敛速度较慢或容易落入局部最优的缺陷。
鲸鱼优化算法(Whale Optimization Algorithm,WOA)是依据鲸鱼围捕猎物的行为提出的一种智能优化算法[11]。WOA需设置的参数较少、结构简单,适用于SVM模型的参数优化,但收敛速度较慢,且优化结果容易陷入局部最优。因此,为提高WOA的收敛速度,避免WOA在寻优过程中过早地陷入局部最优,提出一种改进鲸鱼优化算法(Improved Whale Optimization Algorithm,IWOA),从鲸鱼种群初始化、调节因子非线性化及随机差分进化(Differential Evolution,DE)3个方面入手对WOA进行改进。在此基础上,提出一种基于IWOA−SVM的煤矿突水预测模型,基于IWOA结构简单、易实现、寻优能力强的优点[11],结合DE算法和混沌映射方法的特性改善WOA的全局搜索能力,对SVM的惩罚因子和核函数宽度进行寻优,从而提高突水预测的准确率和效率。
1. 基本原理
1.1 鲸鱼优化算法基本原理
在WOA中,每头鲸鱼的位置代表问题的1个解,猎物的位置则指代问题的最优解。WOA分为开发阶段和搜索阶段:在开发阶段,每只鲸鱼都可以随机选择包围猎物行为或螺旋泡沫网攻击行为,螺旋状上升游动并喷出气泡来包围搜捕猎物;探索阶段的鲸鱼则游走觅食,远离当前最优参考位置,使算法具有一定的探索能力。
1.1.1 开发阶段
(1) 包围猎物。捕捉猎物时,鲸鱼首先确定猎物的位置,然后包围猎物。包围猎物的行为可描述为
$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}^*}(t) - {\boldsymbol{A}} \left| {{\boldsymbol{C}}{{\boldsymbol{X}}^*}({t}) - {\boldsymbol{X}}(t)} \right| $$ (1) 式中:X*(t),X(t)分别为迭代第t次时的最优位置向量和个体位置向量;A,C为系数向量,计算公式为
$$ \left\{ \begin{gathered} {\boldsymbol{A}} = 2a {{\boldsymbol{r}}_{\text{1}}} - a \hfill \\ {\boldsymbol{C}} = 2 {{\boldsymbol{r}}_2} \hfill \\ \end{gathered} \right. $$ (2) 式中:a为调节因子,
${a} = 2 - 2 \dfrac{{t}}{{{t_{\max }}}}$ ,tmax为最大迭代次数;r1,r2为[0,1]的随机向量。(2) 螺旋泡沫网攻击。鲸鱼沿着螺旋状的轨迹运动,缩小包围猎物的圆圈,最后捕捉猎物。该过程主要通过收缩包围机制和螺旋更新位置2种行为描述,由于这2种行为是同时发生的,所以每只鲸鱼在该过程中随机选择一种方式更新自己的位置。位置更新公式为
$$ {\boldsymbol{X}}(t + 1) = \left\{ \begin{gathered} {{\boldsymbol{X}}^*}(t) - {\boldsymbol{A}} D \hfill \\ D {\exp {\left( {bl} \right)}} \cos (2{\text{π}} l) + {{\boldsymbol{X}}^*}(t) \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {} \\ {} \end{array}\begin{array}{*{20}{c}} {p < 0.5} \\ {p \geqslant 0.5} \end{array} $$ (3) 式中:D为迭代第t次时个体鲸鱼到目标的距离,
$D = \left| {{{\boldsymbol{X}}^*}(t) - {\boldsymbol{X}}(t)} \right|$ ;b为常数;l为[−1,1]的随机数;p为策略选择阈值,取值范围为[0,1]。1.1.2 搜索阶段
在搜索阶段,WOA会随机选取一头鲸鱼,以该鲸鱼位置作为参考,迫使鲸鱼远离当前最优解的位置,寻找更好的猎物,其数学模型为
$$ {\boldsymbol{X}}(t + 1) = {{\boldsymbol{X}}_{{{\rm{rand}}}}}(t) - {\boldsymbol{A}} |{\boldsymbol{C}}{{\boldsymbol{X}}_{{\rm{rand}}}}({t}) - {\boldsymbol{X}}(t)| $$ (4) 式中Xrand(t)为迭代第t次时鲸鱼种群中任意选择的一个鲸鱼的位置向量。
1.2 SVM基本原理
SVM模型可以较好地解决如煤矿突水预测这类具备高维数、小样本、非线性特征的分类问题[8-9,12]。SVM的核心思想:对于一个在原始低维空间中难以处理的非线性问题,在核函数的作用下,将其转变成一个更高维特征空间中的线性可分问题;在高维空间中找到一个分割样本的超平面,使得分布在其两边的两类样本中,距离它最近的样本对象之间的距离最大。对于给定的训练样本
$M = \{ ({{\boldsymbol{x}}_1},{{\boldsymbol{y}}_1}),({{\boldsymbol{x}}_2},{{\boldsymbol{y}}_2}), $ … ,$({{\boldsymbol{x}}_m},{{\boldsymbol{y}}_m})\} $ (m为训练样本总数),输出向量${{\boldsymbol{y}}_I} \in \{ - 1,1\}$ ,基于结构风险最小化原则建立的分类函数为$$ f({\boldsymbol{x}}_I) = {\rm{sign}}\left(\sum\limits_{I = 1,J = 1,I \ne J }^m {{\alpha _I}{{\boldsymbol{y}}_I}k({{\boldsymbol{x}}_{I}},{{\boldsymbol{x}}_J}) + {d}} \right)\begin{array}{*{20}{c}} {}&{0 < {\alpha _I} < c} \end{array} $$ (5) 式中:xI、xJ为输入特征向量;αI为拉格朗日乘子;k(xI, xJ)为核函数;c为惩罚因子;d为阈值。
核函数是SVM解决非线性分类问题的核心。目前应用最广泛的核函数主要包括线性核函数、多项式核函数、Sigmoid核函数及高斯径向基核函数(Radial Basis Function, RBF) 4种。本文选用其中泛化能力较好的RBF核函数作为SVM的核函数,其具体表达式为
$$ k({{\boldsymbol{x}}_{{I}}},{{\boldsymbol{x}}_J}) = \exp \left( { { - \frac{{{{\left\| {{{\boldsymbol{x}}_{{I}}} - {{\boldsymbol{x}}_J}} \right\|}^2}}}{{2{\sigma ^2}}}} } \right) $$ (6) 式中σ为核函数的宽度。
2. 基于IWOA−SVM的煤矿突水预测模型
2.1 参数优化
构建煤矿突水预测模型时,为了获取更加精确的预测结果,需要优化SVM模型的惩罚因子c和核函数宽度σ。本文从鲸鱼种群初始化、调节因子非线性化及随机DE 3个方面入手对WOA进行改进,并将改进后的算法IWOA用于SVM参数寻优。
2.1.1 种群初始化
传统WOA使用随机初始化方法来确定初代鲸鱼种群的位置,随后每一个鲸鱼都会在不断迭代中向着最优位置靠近,直到算法收敛或达到最大迭代次数。如果鲸鱼个体的初始位置与最优位置很近,那么该鲸鱼很快就会到达最优位置,算法的收敛速度就会很快。但是随机初始化方法在大多数情况下很难保证鲸鱼初始位置距离最优位置很近。
针对这一缺陷,本文基于混沌映射的随机性、遍历性等特点丰富鲸鱼种群的多样性,提高鲸鱼种群寻找到最优猎物的可能性。大量研究表明[13-15],将混沌映射应用在优化领域代替伪随机数生产器生成混沌数,常常能取得比伪随机数更好的效果。常用的混沌映射主要包括Logistic映射、Gussian 映射、Sine映射、Tent映射等。其中Tent映射在分布上更加均匀,能使算法的搜索效率更高,因此,本文使用Tent映射初始化鲸鱼种群,初始化公式为
$$ {{\boldsymbol{X}}}_{i+1}=\left\{ \begin{array}{l}{{\boldsymbol{X}}}_{i}/0.6\\ (1 -{\boldsymbol{X}}_{i})/(1-0.6)\end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}0 < {{\boldsymbol{X}}}_{i}\leqslant 0.6\\ 0.6 < {{\boldsymbol{X}}}_{i}\leqslant 1 \end{array} \right.$$ (7) 式中Xi为第i个鲸鱼个体的初始位置向量。
2.1.2 调节因子非线性化
WOA通过调节因子a控制全局搜索能力,a值越大,则算法在全局搜索上的表现力越强,在局部搜索上的表现力则相对较弱。原始调节因子a在迭代过程中线性地从2减小到0,这种线性变化难以应对复杂问题,在优化时易陷入局部最优。针对该问题,本文提出一种非线性变化策略,使调节因子a在整个迭代过程中从2到0先慢后快地减小,提升算法在迭代前期的全局搜索能力及迭代后期的局部搜索能力,从而加快收敛速度。优化后a的计算公式为
$$ {a} = 2 - 2 {(t/{t_{\max }})^2} $$ (8) 2.1.3 DE算法
WOA在寻优时所有鲸鱼会朝着当前最优位置的鲸鱼个体靠近,因此,若当前最优位置不是全局最优解,则整个种群就会错误地向局部最优聚拢,算法会陷入局部最优。针对这一缺点,本文引入DE算法的变异、交叉、选择操作,以增强WOA的全局搜索能力。
(1) 变异。从鲸鱼种群中随机选择2个鲸鱼个体并生成差分向量,然后选择另外一个鲸鱼个体与加权差分向量求和,生成变异个体。变异个体计算公式为
$$ {{\boldsymbol{h}}_i}(t) = {{\boldsymbol{X}}_{1}}(t) + F ({{\boldsymbol{X}}_{2}}(t) - {{\boldsymbol{X}}_{3}}(t)) $$ (9) 式中F为缩放因子,F∈[0,2]。
(2) 交叉。将选定的目标鲸鱼
$ {{\boldsymbol{X}}_i}(t) = \{ {{\boldsymbol{X}}_{i,1}}(t), $ $ {{\boldsymbol{X}}_{i,2}}(t), \cdots , {{\boldsymbol{X}}_{i,n}}(t)\} $ (n为鲸鱼个体的维数)与变异产生的新鲸鱼${{\boldsymbol{h}}_i}(t) = \{ {{\boldsymbol{h}}_{i,1}}(t), $ $ {{\boldsymbol{h}}_{i,2}} (t), \cdots , {{\boldsymbol{h}}_{i,n}}(t)\}$ 进行交叉操作,从而生成新的子代鲸鱼个体$ {{\boldsymbol{u}}_i}(t) = \{ {{\boldsymbol{u}}_{i,1}}(t),{{\boldsymbol{u}}_{i,2}}(t), \cdots , {{\boldsymbol{u}}_{i,n}}(t)\} $ ,增加鲸鱼种群的多样性。交叉操作的表达式为$$ {{\boldsymbol{u}}_{i,j}} = \left\{ \begin{gathered} {{\boldsymbol{h}}_{i,j}}(t) \begin{array}{*{20}{c}} {}&{{\rm{rand}}(0,1) \leqslant q} \end{array} \hfill \\ {{\boldsymbol{X}}_{i,j}}(t) \begin{array}{*{20}{c}} {}&{{\rm{rand}}(0,1) > q} \end{array} \hfill \\ \end{gathered} \right. $$ (10) 式中:
$j = 1,2, \cdots ,n $ ;q为交叉概率,q∈[0,1]。(3) 选择。在目标鲸鱼和子代鲸鱼之间进行选择操作,将表现更好的鲸鱼个体保留到下一代鲸群中,选择公式为
$$ {{\boldsymbol{X}}_i}(t + 1) = \left\{ \begin{gathered} {{\boldsymbol{u}}_i}(t)\begin{array}{*{20}{c}} {}&{S({{\boldsymbol{u}}_i}(t)) \leqslant S({{\boldsymbol{X}}_i}(t))} \end{array} \hfill \\ {{\boldsymbol{X}}_i}(t)\begin{array}{*{20}{c}} {}&{S({{\boldsymbol{u}}_i}(t)) > S({{\boldsymbol{X}}_i}(t))} \end{array} \hfill \\ \end{gathered} \right. $$ (11) 式中S( )为适应度函数。
2.2 预测流程
煤矿突水受到多种因素的影响,本文将影响煤矿突水的多种因素作为模型的输入特征向量,突水与安全2种突水结果作为数据的类别信息构成模型的输出向量。
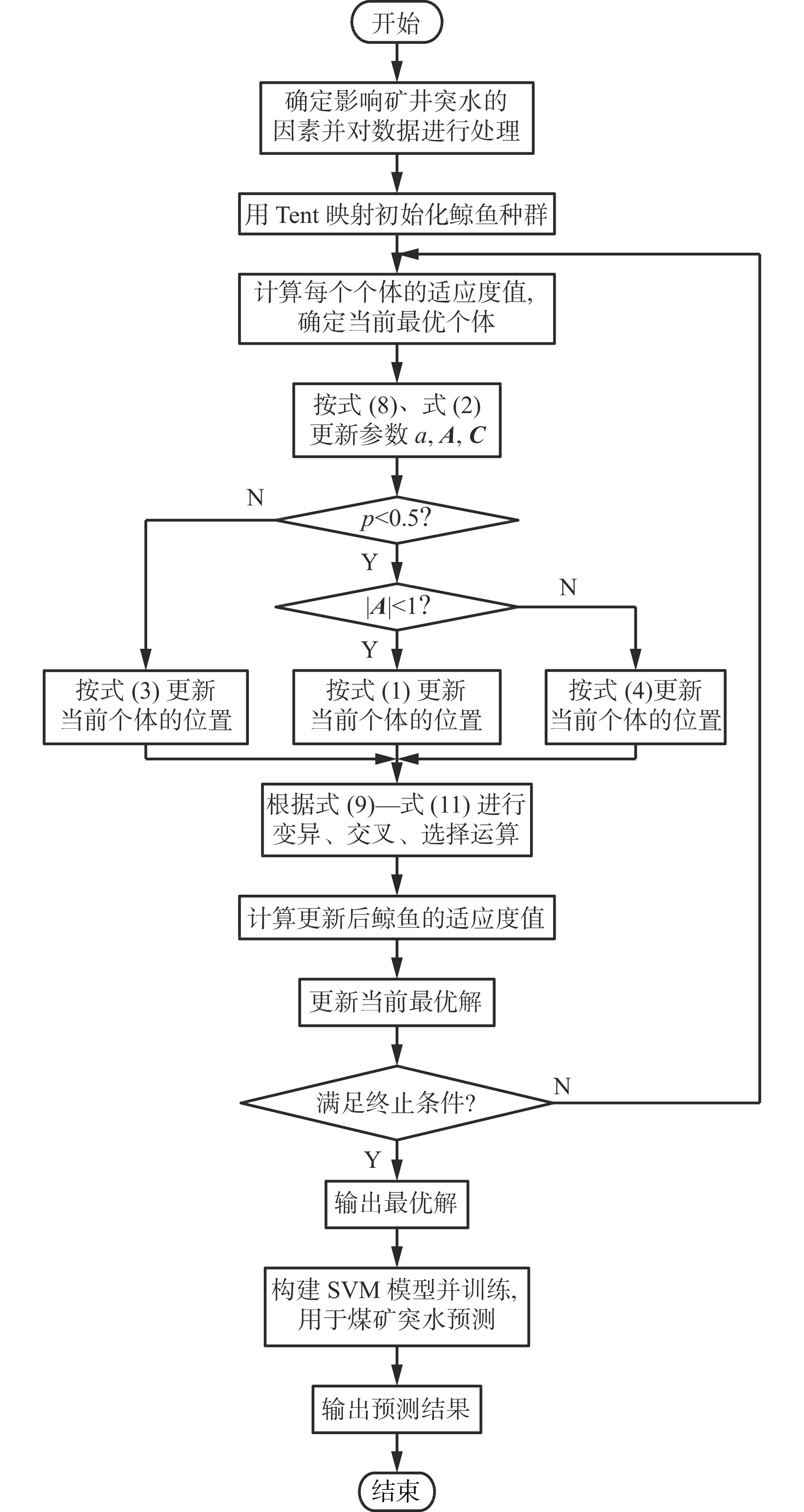
构建IWOA−SVM突水预测模型时,首先要实现IWOA。每个鲸鱼个体由SVM的核函数宽度和惩罚因子2个参数构成,以突水预测结果与实际结果间的误差最小化为目标建立目标函数,根据IWOA得到SVM模型的最优参数值。采用SVM模型对样本数据进行预测,得出最终的突水预测结果。基于IWOA−SVM的煤矿突水预测流程如图1所示。
3. 实验分析
3.1 模型输入特征与数据处理
矿井突水是指在采掘过程中带压水通过裂隙等突水通道涌入巷道的现象,一般指底板承压含水层水突出。本文从突水水源、突水通道、影响突水指标3个角度出发分析突水机理,从而确定作为预测模型输入特征的相关影响因素。
研究表明[16-19],煤层底板下的承压含水层是煤矿突水的物质基础,含水层的富水性对矿井突水量大小起决定性作用。水压是导致底板突水的力源,而底板隔水层则对底板突水起抑制作用,隔水层越厚,抑制突水的能力越强。断层与裂隙是底板突水的主要充水通道,断层落差越大的地点越容易发生煤层底板突水,而陷落柱等地质构造与裂隙发育都有可能形成突水通道,加大突水概率。采高和煤层倾角均会影响矿井的充水强度,当煤层倾角和采高较大时会增加地下地层的压力,减小隔水层厚度,增大突水概率,此外煤层开采后的垮落高度也会较大,塌陷及裂隙可能沟通含水层,从而造成突水。因此,在构建突水预测模型时,可以针对不同矿井的实际情况进行分析,选择合适的影响因素,对模型的输入特征进行调整。
本文收集整理了华北典型矿区的实测突水资料,根据华北典型矿区水文地质特征,将水压
$z $ 1、隔水层厚度$z $ 2、煤层倾角$z $ 3、断层落差$z $ 4、断层距工作面距离$z $ 5、采高$z $ 6共6个影响因素作为预测模型的输入特征。从突水资料中选取55条数据构建数据样本集,其中43个样本作为训练样本,其余12个样本作为测试样本。原始数据还存在各属性参数的量纲和数量级不同的问题,如水压的单位为帕(Pa),煤矿底板隔水层厚度的单位为米(m),不同的量纲和数量级都会影响预测结果的准确性。为了消除量纲和数量级不同的影响,在进行预测之前,先对数据集进行归一化处理,将样本的特征值转换到[0,1]区间中,具体公式为
$$ {{z}^*} = \frac{{z - {z_{{\text{min}}}}}}{{{z_{\max }} - {z_{\min }}}} $$ (12) 式中:
${z^*} $ 为归一化后的参数;$z $ 为原始参数;${z_{\max }} $ ,${z_{\min }} $ 为样本数据中的最大值和最小值。归一化处理后的部分突水数据见表1,其中突水状态中1表示突水,0表示不突水。
表 1 归一化处理后的部分突水数据Table 1. Partial water inrush data after normalization样本编号 水压z1 隔水层厚度z2 煤层倾角z3 断层落差z4 断层与工作面距离z5 采高z6 突水状态 1 0.383 4 0.199 4 0.466 7 0.080 0 0.123 1 0 1 2 0.339 4 0.188 5 0.800 0 1.000 0 0.692 3 0.111 1 1 7 0.256 4 0.400 7 0.133 3 0.016 0 0.476 9 0.006 9 0 8 0.172 3 0.258 0 0.533 3 0.064 0 0.061 5 0.090 3 1 12 0 0.325 5 0.066 7 0.440 0 0.046 2 0.013 9 0 19 0.158 0 0.209 4 0.066 7 0.020 0 0.423 1 0.090 3 0 25 0.497 4 0.453 5 0.333 3 0.035 0 0.061 5 0.152 8 1 32 0.196 9 0.070 6 0.400 0 0.300 0 0.123 1 0.111 1 1 34 0.717 6 0.560 4 0.400 0 0.070 0 0.092 3 0.251 4 1 42 0.300 5 0.451 5 0.566 7 0.024 0 0.053 8 0.097 2 0 43 0.373 1 0.451 5 0.600 0 0.220 0 0.276 9 0.097 2 0 3.2 参数确定
使用Python实现IWOA对SVM模型的参数寻优。将标准误差作为模型的评价指标,同时,通过对比PSO算法、DE算法、WOA、IWOA的寻优结果,评估IWOA的整体性能。
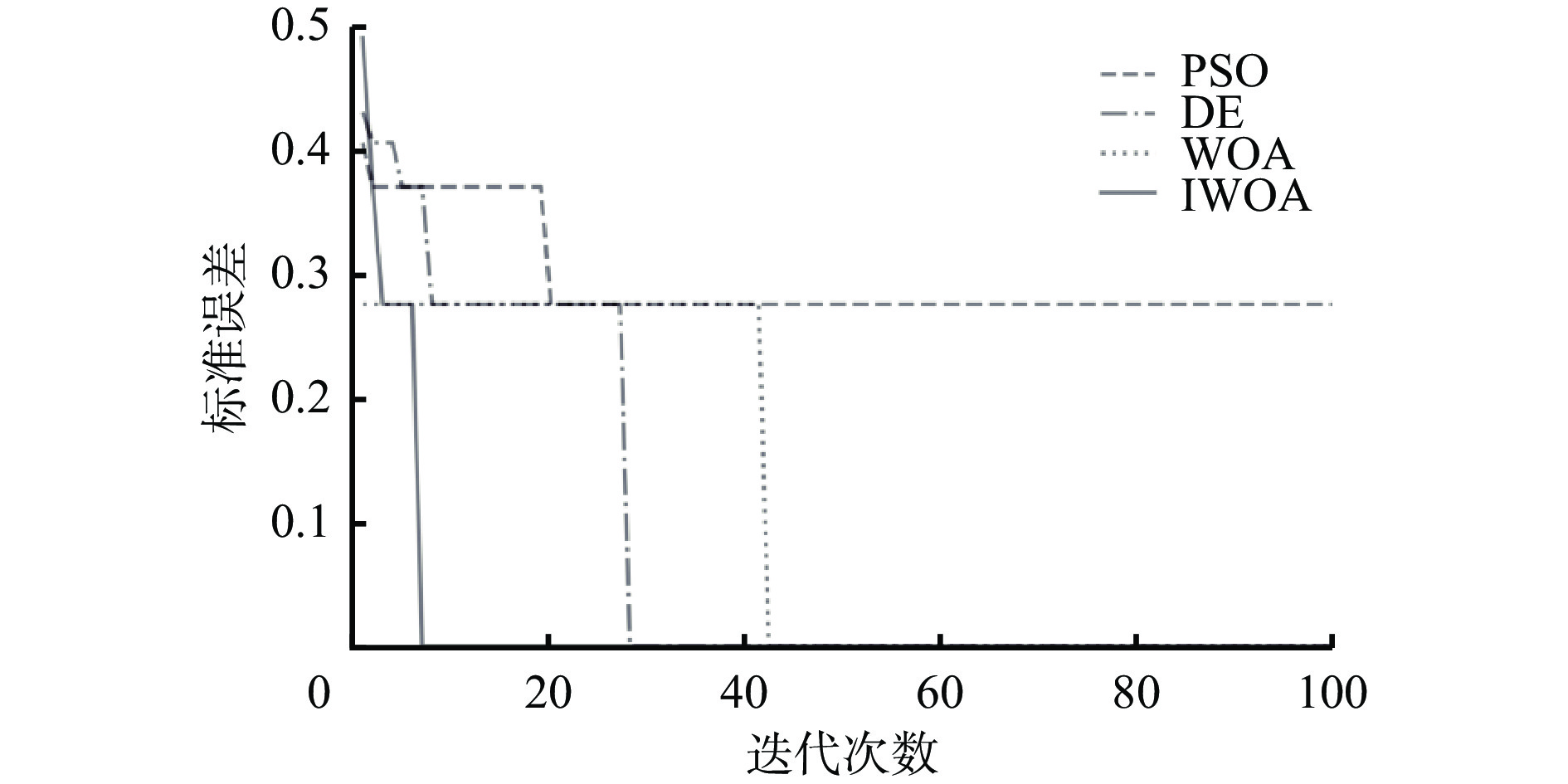
基于公平性原则,设置算法的种群大小均为35,最大迭代次数均为100,每个种群个体均是由SVM的参数c和σ构成的二维向量,参数范围均为[0.01,100]。4种算法的寻优结果见表2,收敛曲线如图2所示。
表 2 4种算法的寻优结果Table 2. Optimizing results of four algorithms算法 寻优结果 准确率/% 标准
误差收敛
代数c σ PSO 4.358 0.010 60.47 0.489 100 DE 7.208 0.325 83.72 0.386 29 WOA 29.136 0.066 81.39 0.408 43 IWOA 6.517 0.418 88.37 0.333 8 分析表2结果可知,IWOA对训练集的预测准确率为88.37%,PSO算法的准确率为60.47%,DE算法的准确率为83.72%,WOA的预测准确率为81.39%。相比于PSO算法、DE算法、WOA,本文提出的IWOA的预测准确率最高,标准误差也最小,说明其收敛精度高,并且稳定性更强,鲁棒性好。由图2可以直观地看出,IWOA在寻优过程中迭代到第8次时标准误差已经收敛到最小值,PSO算法在迭代到100次时仍未收敛到最小值,而DE算法、WOA分别迭代到29次及43次时才收敛到最小值,说明IWOA的寻优能力更强且收敛速度更快。
使用IWOA对SVM模型的参数进行寻优,最终确定基于IWOA−SVM的煤矿突水预测模型的2个参数分别为c = 6.517,σ = 0.418。
3.3 突水预测结果
煤矿突水预测是一个二分类问题,本文使用预测准确率作为评价指标,预测准确率越接近1,表明突水预测模型的预测结果越准确。
使用IWOA计算出的最优惩罚因子和核函数宽度参数构建SVM模型,对测试样本进行预测,模型预测结果与实际结果如图3所示。可以看出,基于IWOA−SVM的模型对12个测试样本的预测结果与实际突水结果均重叠。
为了验证本文所提算法应用于煤矿突水预测时的准确性,在相同的数据集和实验条件下,使用传统的突水系数法、SVM、WOA−SVM及IWOA−SVM分别进行煤矿突水预测,并对预测结果进行比较,见表3。
表 3 不同方法预测结果比较Table 3. Comparison of prediction results of different methods序号 实际结果 预测结果 突水系数法 SVM WOA−SVM IWOA−SVM 44 0 0 1 0 0 45 1 0 1 1 1 46 0 0 0 0 0 47 0 0 0 0 0 48 0 0 0 0 0 49 1 1 1 1 1 50 0 0 1 0 0 51 1 0 1 0 1 52 1 0 1 1 1 53 0 0 0 0 0 54 1 1 1 1 1 55 1 1 1 1 1 从表3可以看出,传统突水系数法、SVM及WOA−SVM在突水测试集上的预测准确率分别为75%、83.33%和91.67%,而本文提出的IWOA−SVM在是否突水这一分类问题上的预测准确率达到100%,预测结果与实际结果相符。
分析IWOA−SVM算法的特性,IWOA在寻优前期的全局搜索能力强、在迭代后期的局部搜索能力强这一特质能够加快IWOA在搜索SVM模型最优参数时的收敛速度,每个鲸鱼拥有的交叉、变异、选择能力增强了IWOA的全局搜索能力,避免了其在寻优过程中过早陷入局部最优,这是WOA−SVM无法做到的。因此,IWOA−SVM模型在煤矿突水预测中表现出更高的准确率和稳定性。
4. 结论
(1) IWOA引入非线性思想优化调节因子,利用混沌映射和差分进化的思想优化鲸鱼种群,从而提高传统WOA的全局搜索能力及收敛速度。
(2) 根据煤矿突水数据小样本、非线性的特征,选取SVM模型进行突水预测。为了确定SVM的最优参数,有效提高预测精度和速度,基于IWOA对其进行参数寻优。
(3) 实验结果表明:与PSO算法、DE算法、WOA相比,IWOA的预测准确率最高,标准误差最小,且收敛速度快,鲁棒性好;IWOA−SVM的预测准确率达到100%,与传统的突水系数法、SVM、WOA−SVM相比,IWOA−SVM表现出更高的准确率和稳定性。
-
表 1 归一化处理后的部分突水数据
Table 1 Partial water inrush data after normalization
样本编号 水压z1 隔水层厚度z2 煤层倾角z3 断层落差z4 断层与工作面距离z5 采高z6 突水状态 1 0.383 4 0.199 4 0.466 7 0.080 0 0.123 1 0 1 2 0.339 4 0.188 5 0.800 0 1.000 0 0.692 3 0.111 1 1 7 0.256 4 0.400 7 0.133 3 0.016 0 0.476 9 0.006 9 0 8 0.172 3 0.258 0 0.533 3 0.064 0 0.061 5 0.090 3 1 12 0 0.325 5 0.066 7 0.440 0 0.046 2 0.013 9 0 19 0.158 0 0.209 4 0.066 7 0.020 0 0.423 1 0.090 3 0 25 0.497 4 0.453 5 0.333 3 0.035 0 0.061 5 0.152 8 1 32 0.196 9 0.070 6 0.400 0 0.300 0 0.123 1 0.111 1 1 34 0.717 6 0.560 4 0.400 0 0.070 0 0.092 3 0.251 4 1 42 0.300 5 0.451 5 0.566 7 0.024 0 0.053 8 0.097 2 0 43 0.373 1 0.451 5 0.600 0 0.220 0 0.276 9 0.097 2 0 表 2 4种算法的寻优结果
Table 2 Optimizing results of four algorithms
算法 寻优结果 准确率/% 标准
误差收敛
代数c σ PSO 4.358 0.010 60.47 0.489 100 DE 7.208 0.325 83.72 0.386 29 WOA 29.136 0.066 81.39 0.408 43 IWOA 6.517 0.418 88.37 0.333 8 表 3 不同方法预测结果比较
Table 3 Comparison of prediction results of different methods
序号 实际结果 预测结果 突水系数法 SVM WOA−SVM IWOA−SVM 44 0 0 1 0 0 45 1 0 1 1 1 46 0 0 0 0 0 47 0 0 0 0 0 48 0 0 0 0 0 49 1 1 1 1 1 50 0 0 1 0 0 51 1 0 1 0 1 52 1 0 1 1 1 53 0 0 0 0 0 54 1 1 1 1 1 55 1 1 1 1 1 -
[1] 陈恋, 袁梅, 向维, 等. PCA−Fisher判别模型在煤层底板突水预测中的应用[J]. 数学的实践与认识,2021,51(6):103-111. CHEN Lian, YUAN Mei, XIANG Wei, et al. Application of PCA-Fisher discriminant model in prediction of water inrush from coal seam floor[J]. Mathematics in Practice and Theory,2021,51(6):103-111.
[2] 张立新, 李长洪, 赵宇. 矿井突水预测研究现状及发展趋势[J]. 中国矿业,2009,18(1):88-90. DOI: 10.3969/j.issn.1004-4051.2009.01.025 ZHANG Lixin, LI Changhong, ZHAO Yu. State of research on prediction and forecast of groundwater inrush in mine and its development trend[J]. China Mining Magazine,2009,18(1):88-90. DOI: 10.3969/j.issn.1004-4051.2009.01.025
[3] 国家煤矿安全监察局. 煤矿防治水细则[M]. 北京: 煤炭工业出版社, 2018. State Administration of Coal Mine Safty. Rules for coal mine water prevention and control[M]. Beijing: China Coal Industry Publishing House, 2018.
[4] 潘晖, 王继尧. 基于粒子群优化神经网络的煤层底板突水预测[J]. 山西焦煤科技,2009(1):34-36. DOI: 10.3969/j.issn.1672-0652.2009.01.013 PAN Hui, WANG Jiyao. Forecast for water-inrush from coal floor based on neural networks trained by particle swarm optimization[J]. Shanxi Coking Coal Science & Technology,2009(1):34-36. DOI: 10.3969/j.issn.1672-0652.2009.01.013
[5] 宋国娟. 基于极限学习机的煤矿突水预测及避险路线优化研究[D]. 徐州: 中国矿业大学, 2016. SONG Guojuan. Research on mine water inrush prediction based on extreme learning machine and route optimization[D]. Xuzhou: China University of Mining and Technology, 2016.
[6] WANG Ge, WEI Junjie, YAO Banghua. A coal mine water inrush prediction model based on artificial intelligence[J]. International Journal of Safety and Security Engineering,2020,10(4):501-508. DOI: 10.18280/ijsse.100409
[7] 师煜, 朱希安, 王占刚, 等. 基于GAPSO−RFR的矿井底板突水预测模型与应用[J]. 中国矿业,2020,29(8):152-157. SHI Yu, ZHU Xi'an, WANG Zhangang, et al. Forecast model of mine floor water inrush based on genetic particle swarm optimization and random forest regression and its application[J]. China Mining Magazine,2020,29(8):152-157.
[8] 李颖. 基于支持向量机的煤层底板突水预测方法研究[D]. 北京: 煤炭科学研究总院, 2007. LI Ying. Research on prediction method of coal seam floor water inrush based on support vector machine [D]. Beijing: China Coal Research Institute, 2007.
[9] 张风达, 申宝宏. 深部煤层底板突水危险性预测的PSO_SVM模型[J]. 煤炭科学技术,2018,46(7):61-67. ZHANG Fengda, SHEN Baohong. PSO_SVM prediction model for evaluating water inrush risk from deep coal seam floor[J]. Coal Science and Technology,2018,46(7):61-67.
[10] 李腾, 朱希安, 王占刚. 矿井突水水源判别的FOA−LSSVM模型[J]. 北京信息科技大学学报(自然科学版),2020,35(3):41-45. LI Teng, ZHU Xi'an, WANG Zhangang. FOA-LSSVM model for source identification of mine water inrush[J]. Journal of Beijing Information Science & Technology University(Natural Science Edition),2020,35(3):41-45.
[11] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software,2016,95:51-67. DOI: 10.1016/j.advengsoft.2016.01.008
[12] 宰慧. 基于PSO−SVM的煤层底板突水危险性预测研究[D]. 青岛: 山东科技大学, 2017. ZAI Hui. The coal floor water-inrush risk prediction research based on the PSO-SVM[D]. Qingdao: Shandong University of Science and Technology, 2017.
[13] 赵欣. 不同一维混沌映射的优化性能比较研究[J]. 计算机应用研究,2012,29(3):913-915. DOI: 10.3969/j.issn.1001-3695.2012.03.031 ZHAO Xin. Research on optimization performance comparison of different one-dimensional chaotic maps[J]. Application Research of Computers,2012,29(3):913-915. DOI: 10.3969/j.issn.1001-3695.2012.03.031
[14] 李雪岩, 李雪梅, 李学伟, 等. 基于混沌映射的元胞遗传算法[J]. 模式识别与人工智能,2015,28(1):42-49. LI Xueyan, LI Xuemei, LI Xuewei, et al. Cellular genetic algorithm based on chaotic map[J]. Pattern Recognition and Artificial Intelligence,2015,28(1):42-49.
[15] 赵宇, 彭珍瑞. 混沌鲸鱼优化算法及其在有限元模型修正中的应用[J]. 兰州交通大学学报,2021,40(1):39-45. ZHAO Yu, PENG Zhenrui. Whale optimization algorithm with chaotic maps and its application in finite element model updating[J]. Journal of Lanzhou Jiaotong University,2021,40(1):39-45.
[16] 刘伟韬. 矿井水害与防治[M]. 北京: 煤炭工业出版社, 2016. LIU Weitao. Mine water disaster and prevention[M]. Beijing: China Coal Industry Publishing House, 2016.
[17] 石秀伟, 胡耀青, 张和生. 基于GIS的煤层底板突水预测理论模型[J]. 太原理工大学学报,2008,38(增刊2):244-246. SHI Xiuwei, HU Yaoqing, ZHANG Hesheng. GIS-based forecasting model of floor water bursting in coal mines[J]. Journal of Taiyuan University of Technology,2008,38(S2):244-246.
[18] NIU Huigong, WEI Jiuchuan, YIN Huiyong. An improved model to predict the water-inrush risk from an Ordovician limestone aquifer under coal seams: a case study of the Longgu Coal Mine in China[J]. Carbonates and Evaporites,2020,35(3):1-16.
[19] SHI Longqing, GAO Weifu, HAN Jin, et al. A nonlinear risk evaluation method for water inrush through the seam floor[J]. Mine Water and the Environment,2017,36:597-605. DOI: 10.1007/s10230-017-0449-1
-
期刊类型引用(2)
1. 刘大鹏,张思睿. 基于CUDA并行计算的煤矿奥灰突水快速准确预测方法. 承德石油高等专科学校学报. 2024(02): 9-12+59 .  百度学术
百度学术
2. 唐晓骞,王韬,万国祥,李志勇. 基于无人机倾斜摄影的露天煤矿边坡检测方法. 自动化与仪器仪表. 2023(09): 87-91 .  百度学术
百度学术
其他类型引用(1)

























 下载:
下载: